Segner János András a pozsonyi evangélikus líceumban, majd egy évig a debreceni református kollégiumban tanult. A jénai egyetemen szerzett orvosdoktori diplomát. Rövid ideig Pozsonyban, majd egy évig Debrecenben folytatott orvosi gyakorlatot. 1732-től három évig a jénai egyetemen tanított matematikát, fizikát és kémiát. Ezt követően húsz éven keresztül a göttingeni Georgia Augusta egyetem professzora volt, nyilvános előadásaiban elsősorban matematikát és fizikát tanított. 1755 tavaszán családjával Halléba költözött, ahol a Friedrich egyetemen rendkívül kedvező feltételek mellett kezdhette meg professzori működését. Elsősorban matematikát és fizikát adott elő 22 éven keresztül, haláláig.
Most matematikatanári tevékenységéből emelünk ki egy kis részt.
Segner egyik legjelentősebb tankönyvét Az aritmetika és a geometria elemei című művet fia, Johann Wilhelm Segner németre fordította, Édesapja átjavította, kiegészítette. Az két alkalommal is megjelent Halléban, 1764-ben és 1773-ban.
A kor szokásainak megfelelően az 1773. évi kiadás címoldalán a szerző rangjainak, beosztásainak felsorolása után következik csak a mű címe: ‘Anfangsgründe der Arithmetik, Geometrie und der geometrischen Berechnungen aus dem lateinischen übersetz. Zweite Auflage von der Verfasser selbst durchaus gebessert und vermehret. Mit Kupfern. Halle, ...Rengerischen Buchhandlung, 1773.’ [...latinból fordítva. A szerző által teljesen átjavított és kibővített második kiadás. Rézmetszetekkel. Rengerisch Könyvkereskedés]
Érdekes, hogy a címoldalon nem szerepel a fordító neve, ezt csak a szerzőnek Halléban 1773. április 26-án írt előszavából tudhatjuk meg:
„Fiam fordításának jelenlegi közreadásához nincs mit hozzátennem, csupán azt, hogy ezt a kiadást én magam nemcsak a legújabb latin nyelvű változat alapján, hanem sok más helyen is megrövidítettem, ugyanakkor magyarázatokkal láttam el, és kiegészítettem.”
Ezután következik az 1756-os kiadás április 22-én írt előszava. Ezt is azzal kezdte Segner, hogy sokat változtatott az eredeti művön. Átdolgozta, javította, hogy az jól elrendezett, összefüggő legyen. Az a cél vezérelte, hogy azoknak, akik ebből a könyvből tanulnak, olyan alapokat adjon, hogy ők majd további előadásokat és más matematika könyveket is meg tudjanak érteni. Szólt a matematika szépségéről és hasznáról. Hangsúlyozta, hogy azzal kívánta a tanulást megkönnyíteni, hogy érthetően fogalmazott, a tételeket ügyesen rendezte el, a bizonyítások rövidek és meggyőzőek.
Minden egyes fejezetben minden tételt, feladatot, annak következményeit külön paragrafus-számmal jelöl, így könnyen tud a későbbi bizonyításoknál hivatkozni a megfelelő alapismeretekre, tételekre. Összesen 811 paragrafus van a tételes részben, és kilenc további paragrafusban magyarázza el, igen részletesen, a táblázatok használatát. Ugyanis logaritmus-, sinus- és tangenstáblázatok zárják a 492 oldalas könyv szöveges részét.
Érdekes szerkesztésűek Segner táblázatai, bemutatjuk a táblázatok utolsó oldalát.
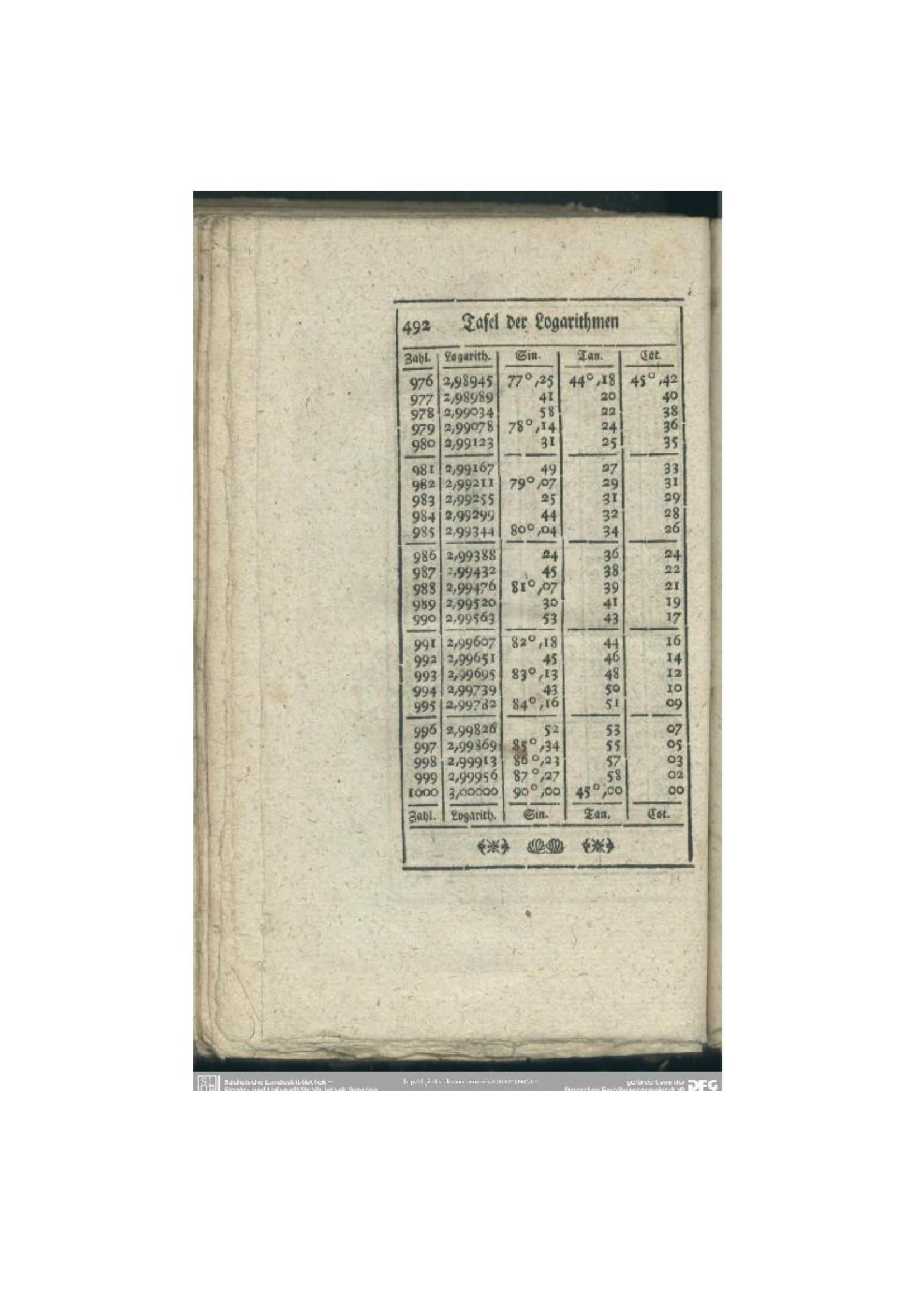1. ábra. Logaritmustáblázat Segner matematikakönyvéből
A könyv legvégén ezután következnek a címoldalon is említett rézmetszetek: XI táblán összesen 188 ábra van. Ezek nagyon jól szerkesztettek, világos elrendezésűek, szükség esetén megfelelően árnyaltak. A térmértani rajzok rendkívül áttekinthetőek, szinte „kiugranak” a lap síkjából.
Most a Pitagorasz-tétel bizonyítását és az ahhoz készített ábrát elemezzük. Amint korábban a Cavalieri-elvnél — amelyet sokáig Segner-elvként emlegettek —, ugyanúgy itt sem írta ki Segner tanár úr a tétel elnevezését.
„Minden tetszőlegesen választott 
derékszögű háromszögben a legnagyobb, 
oldal négyzete akkora, mint a további két oldal, 
és 
négyzeteinek összege.”
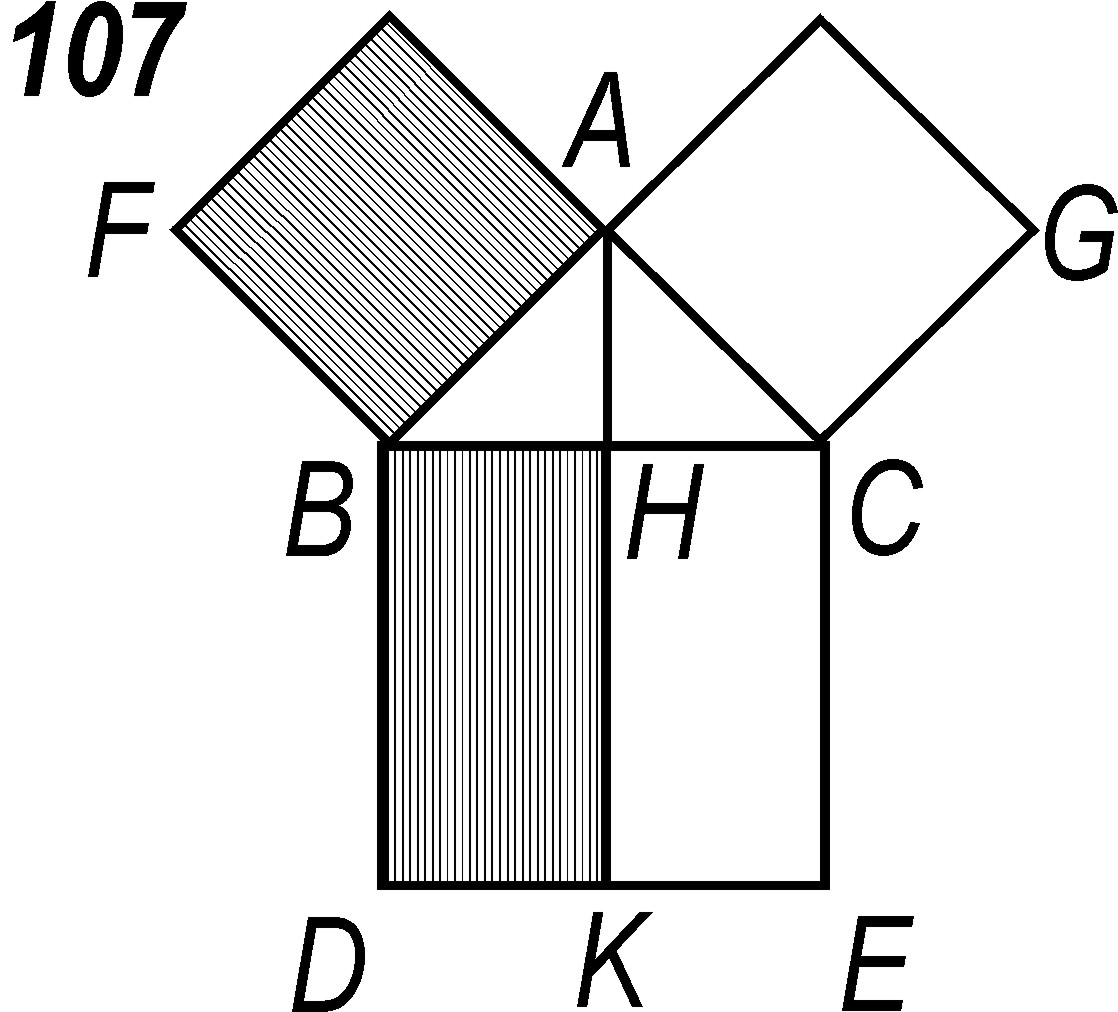
2. ábra. Segner ábrája a Pitagorasz-tételhez
Algebrai módon, négyzetszámokra mondja ki a tételt, a bizonyításhoz tartozó ábrán azonban felrajzolja a négyzeteket. Nem a szokásos — állítólag Pitagorasz által is alkalmazott — átdarabolással bizonyít. Ugyanakkor rendkívül szemléletesen megmutatja, hogy az ábra bal oldalán látható, a kisebbik befogóhoz tartozó, besötétített négyzet területe éppen akkora, mint az átfogóhoz tartozó négyzet bal oldali, ugyancsak besötétített téglalapjának a területe. Ez a téglalap úgy keletkezik, hogy az átfogóhoz tartozó magasságot meghosszabbítja végig az átfogóhoz tartozó négyzeten át. Teljesen hasonló módon, a jobb oldali, a nagyobbik befogóra rajzolt négyzet területe pedig az átfogóhoz tartozó négyzet jobb oldali, téglalapjának a területével egyenlő. A két téglalap területének összege, magától értetődően az átfogóhoz tartozó négyzet területével egyezik meg. A négyzetek és a téglalapok területeinek egyenlőségét a 452. -ban tárgyalt — hasonló háromszögek segítségével belátott — mértani közép összefüggései alapján bizonyítja.
Itt áll előttünk egy példa arra, hogy adott tétel bizonyításához milyen egyszerű, szemléletes módot használ, olyat, amely a segédtétel emlékezetben tartását is segíti. Nem emlékszem arra, hogy eddig találkoztam volna az átfogóhoz tartozó négyzet ilyen egyszerű felosztásával, a mértani középarányos szakaszok ilyen szép, könnyen megjegyezhető ábrázolásával.
Az is nagyszerű Segnernél, hogy további gondolkodásra sarkall. A derékszögű háromszögben található mértani középarányos szakaszok harmadik csoportját is érdemes az ábrába berajzolni: a c átfogóhoz tartozó magasságra rajzolt négyzet területe, 
éppen az átfogó két szeletének, a mostanában szokásos egyszerűbb jelöléssel p-nek és q-nak a szorzatával egyezik. Ez is jól látható lesz, ha Segner ábrájának bal oldali, pc területű, besötétített részében a B csúcstól lefelé a négyzetoldalból kimetsszük a q szakaszt.
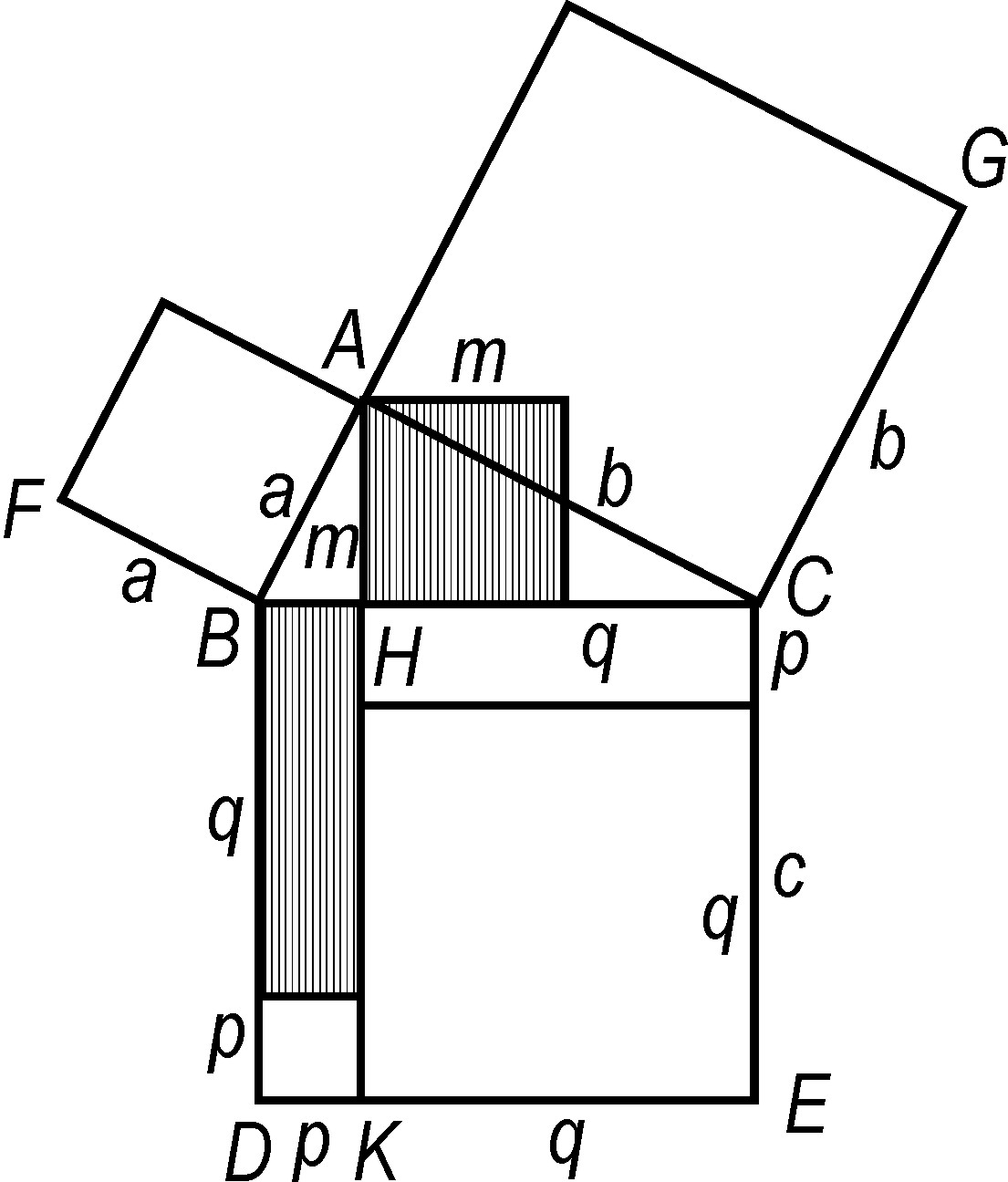
3. ábra. Mértani középarányos szemléltetése
Még tovább is élvezhetjük a matematika szépségét! A bal oldali 
területű téglalapból a 
területű téglalap elvétele után az ábrán lent 
oldalú négyzet marad. Előttünk áll tehát az 
kis derékszögű háromszög oldalaira felírható Pitagorasz-tétel szép rajzolata (a p oldalhoz tartozó négyzet természetesen 
szakasszal lefele eltolva szerepel).
Algebrai ismereteink rögzítéséhez is hozzásegíthet ez az ábra.
A két tag összegének négyzetére vonatkozó összefüggés, a
szépen szemléltethető az átfogóra rajzolt négyzet feldarabolásából: „alul” látható a két kis négyzet, amelyek területe 
, illetve 
, és az átfogó szeleteihez illeszkedik a két területű téglalap.
A továbbiakban Segner eljut a Pitagorasz-tétel általánosításához. Derékszögű háromszög befogóira rajzolt hasonló síkidomok területeinek összege megegyezik az átfogóra rajzolt, az előzőekhez hasonló síkidom területével.
Érdekes módon, nem így, tételként (Lehrsatz) mondja ezt, hanem a 493. -ban is, mit sok más helyen, feladatot (Aufgabe) ad:
„Keressünk, írjunk le olyan alakzatot, amely két hasonló alakzathoz hasonló, és ennek a kettőnek az összegével egyenlő” [a területekről szól a tétel]
A feladathoz tartozó ábrán hasonló négyszögek szerepelnek.
A fenti dolgozat részlet Kovács László: Segner János András, Egy jeles hungarus a 18. századból (Tudománytörténeti és Egészségtudományi Intézet, 2018.) c. könyvéből. A kötet recenziója itt olvasható.
Kovács László