Egy jeles hungarus a 18. századból

2018. március 27-én az MTA könyvtárában mutatta be a szerző — Kovács László — a munkatársaival — Abonyi Iván, Gurka Dezső, Rab Irén, Gazda István — részben közösen írt új munkáját. A könyv címe: Segner János András, két alcímmel. Az első: Egy jeles hungarus a 18. századból. A második: Orvos, matematikus, fizikus, csillagász, vegyész, tanár, filozófus és műszaki alkotó. Az interneten a híres tudósról, J. A. Segnerről csak gyenge minőségű arcképek találhatók. A friss kötet borítóján viszont megjelent F. Reibenstein festő szép színes Segner-portréja.

Eulerről, aki Segner kortársa és közeli munkatársa, több festmény is fennmaradt; azok hamar fellelhetők az interneten. Segner esetében azonban sok-sok fekete-fehér arcképet találunk, melyek leginkább csak az idős professzort mutatják. Ezért is tekinthető egyfajta szenzációnak, hogy az új kötet címlapján megjelent egy Segner-arckép élete derekáról.

J. A. Segner (1704—1777) polihisztort a világ leginkább német tudósként ismeri, de ő saját magát hungarus jelzővel illette. (A segner és hungarus szavak szokásos kiejtése: zégner illetve hungarusz.) Segner evangélikus ősei Stájerországból menekültek hazánkba; a család fiai a török elleni harcokban jeleskedtek, nemesi címet szereztek, Pozsony vármegyében bírói és egyéb elöljárói hivatalokat töltöttek be. Németajkúak voltak, de magyarul is megtanultak. Írásunk címszereplője Pozsony vármegye Szentgyörgy városában született, alsó- és középiskoláit Pozsonyban, Győrben, Debrecenben végezte, 21 évesen már a jénai orvostudományi egyetemen tanult, 1730-ban megszerezve orvosi oklevelét Pozsonyban kezdett praktizálni, majd Debrecen városi orvosa lett. Aztán 1732-ben meghívták Jéna városába magántanárnak; később Göttingen, majd a Halle egyetemén professzorkodott haláláig. Korának egyik legnagyobb tudósaként tartjuk számon. Sokirányú tevékenységének részleteit megtaláljuk a kötetben.

Segner matematikai eredményei. A kötet Segner matematikai munkásságának ismertetésében leginkább Szénássy Barna munkáját követi (Segner András matematikai tevékenysége, Acta Debrecen VI/2. 1960. 37—42.)

A könyv ismerteti Segner azon eredményeit, amelyek a polinomértékek gyors kiszámítására, a polinomgyökök rajzolószerkezetekkel való megszerkesztésére vonatkoznak. Sajnos ez a könyv is elköveti azt a hibát, amit sok elődje: azt jelenti, hogy Segner bizonyította először a Descartes-féle jelszabály (vagy inkább előjelszabály) néven elhíresült észrevételt, mely szerint egy valós együtthatós $p(x)=a_0+a_{1}x+\ldots+a_{n}x^{n}$ polinomnak legfeljebb annyi pozitív gyöke lehet — természetesen multiplicitással tekintve a gyököket —, mint ahányszor átlépünk a nulla felett a számegyenesen, ha sorban lépkedünk az $a_{0},a_{1},\ldots,a_{n}$ számok között. Az igazság az, hogy Segner valóban elsőként adott korrekt bizonyítást, de a módszere csak akkor működik, ha a polinomnak mind az $n$ gyöke valós. Ez pedig így csak fából vaskarika, mert csak akkor mondhatjuk Segner alapján biztosan, hogy például az $x^{7}+x^{5}-8$ polinomnak csak 1 pozitív gyöke van — amely tény történetesen igaz —, ha meggyőződünk arról, hogy mind a 7 gyök valós — amely tény történetesen nem igaz. De például az $x^{5}+8x^{4}+21x^{3}+14x^{2}-20x-24$ polinom estében igaz az, hogy az összes gyök valós, és így Segner nyomán biztosak lehetünk abban, hogy legfeljebb csak 1 pozitív gyök lehet. Viszont nem tűnik könnyebb feladatnak annak ellenőrzése, hogy mind az 5 gyök valós, annak ellenőrzésénél, hogy 4 gyök negatív és 1 gyök pozitív.

Mindazonáltal a Descartes-féle jelszabály helyes észrevétel akkor is, ha nem minden gyök valós, Segner bizonyítása is korrekt, csak hát éppen nem sokra megyünk vele abban a speciális esetben, amikor működik is. De ne legyünk igazságtalanok: Segnernél jelenik először a matematika történetében az a rendkívül fontos tény, hogy $x_{0}$ akkor és csak akkor zérushelye a $p(x)$ polinomnak, ha $(x-x_{0})$ osztja $p(x)$ -et.

Kovács László hosszasan ír arról, hogy Segner felelevenítette a térfogatszámításra vonatkozó Cavalieri-elvet. (Cavalieri egy évszázaddal Segner előtt élt.) Szerencsére Kovács tanár úr már nem vesz mindent készpénznek, amit Segner írt. Utal arra is, hogy a Cavalieri-elv csak nagy gondossággal megfogalmazott feltételek teljesülése esetén alkalmazható. „Láthatjuk tehát, hogy a szabatos tétel erős bizonyításhoz szükség van a matematikai analízisre” — olvashatjuk végkövetkeztetésképpen. Én azonban azt tartanám szükségesnek kijelenteni: a matematikában értelmetlenek a „szabatos tétel” és az „erős bizonyítás” kifejezések, hiszen csak az a bizonyítás, amely korrekt, és minden bizonyítás egyformán erős, illetve csak az a tétel, amelynek már ismerjük legalább egy bizonyítását, így egyik tétel sem szabatosabb a másiknál.¹

A kötet részletesen ismerteti a Segner-féle eljárást is a Ludolf-féle szám közelítő kiszámítására. A $\pi$ -re a következő felső közelítés jön ki: 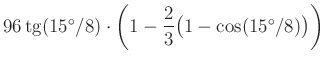$96\operatorname{tg}(15^{\circ}/8)\cdot \left(1-\dfrac{2}{3}\big(1-\cos(15^{\circ}/8)\big)\right)$ . Az viszont megmosolyogtató, hogy Kovács László közli tizedestörtben a fenti értéket: $3{,}14159282\ldots$ Nyilvánvaló ugyanis, hogy ez kalkulátorral vagy számítógéppel kapott érték, amely Segner korában nem volt lehetséges. (A verembe esett róka nem húzhatja ki saját farkánál fogva magát, hiszen a cos és tg függvények pontos értékei kiszámításához okvetlenül szükséges magának a $\pi$ -nek sok-sok tizedesjegye.) Gyökjelekkel és alapműveletekkel kellett volna kiszámolni, hogy mennyi a fenti képlet számértéke felülről becsülve.

Ezekkel olyan formában írható fel a fenti közelítés a $\pi$ számra, amely Segner korában is értelmezhető és közelítőleg kikalkulálható lehetett. Becsülettel végigszámolva azt kapjuk, hogy a Kovács László által közölt közelítő érték utolsó számjegye már hibás, azaz Segner képletének pontos értéke $3{,}14159283$ és $3{,}14159284$ között van.

Segner találta fel a logarléc egyik elődjét is². A logaritmikus skálájú karcolt rézlemezek elkallódtak, csak Segner levelezéseiből tudunk azokról.

Segner matematikusi munkásságából valószínűleg a legmaradandóbbak a Segner-számok, első néhány tagjuk: $P_{2}=1$ , $P_{3}=1$ , $P_{4}=2$ , $P_{5}=5$ , $P_{6}=14$ . Definíció szerint $n>3$ esetén egy konvex $n$ -szög $P_{n}$ különböző módon bontható átlóival $n-2$ darab háromszögre. (A felhasznált átlók nyilván nem metszhetik egymást.) Euler egyik problémája megoldásának legfontosabb részeként Segner megtalálta a következő rekurziót: $P_{n+1}=P_{2}P_{n}+P_{3}P_{n-1}+\ldots+ P_{n-1}P_{3}+P_{n}P_{2}$ . Ennek következményeként hozta ki Euler a következő képletet:

$\displaystyle 2\cdot 3\cdot 4\cdot \ldots\cdot (n-1)P_{n}=2\cdot 6\cdot 10\cdot \ldots\cdot (4n-10).$

A saját rekurziója alapján Segner $n=20$ -ig számolta ki $P_{n}$ értékeit, de néhányat eltévesztett, viszont Goldbach hamar javította őt. Akárhogyan is, Catalan belga matematikus (egy évszázaddal Euler, Segner, Goldbach után) a Segner-számok nevet adta a sorozatnak, de napjainkban a legtöbb matematikus Catalan-számok néven hivatkozik azokra. Az évszázadok során a Segner-számok számtalan helyen felbukkantak. Ajánljuk Richard P. Stanley professzor Catalan Numbers című tavalyi prezentációját és tavalyelőtti http://www.cambridge.org/hu/academic/subjects/mathematics/discrete-mathematics-information-theory-and-coding/catalan-numbers?format=PB&isbn=9781107427747#3P0uI98YhEpH2tGM.97monográfiáját. (A monográfia 242 különböző interpretációt sorol fel.) A jelen recenzió szerzője számára a Segner-számok legkedvesebb származtatása a Pascal-háromszög minden második sorában a legnagyobb és a harmadik legnagyobb érték különbségekénti kiszámolás: $1-0$ , $2-0$ , $6-1$ , $20-6$ , $70-28$ , ...

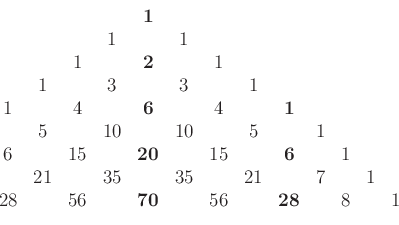
$\begin{displaymath}\begin{array}{cccccccccccccccccccc} & & & & {\bf 1}& & & & & ... ...\ 28& & 56& & {\bf 70}& & 56& & {\bf 28}& & 8& & 1 \end{array}\end{displaymath}$

A Pascal-háromszög részlete

A recenzió tárgyát képező kötetben található Gurka Dezső írása is, amiből megtudható, milyen hatással volt Kant nézeteire Segner szemlélete a számokról.

Összefoglalás. A recenzió alá vont kötet sok-sok értékes adatot tartalmaz, számos érdekes illusztrációt. Tisztelettel javasoljuk a nyájas olvasónak, hogy tegyen egy időutazást: helyezze magát negyed évezreddel korábbi időkbe, és olvasgassa a Gazda István és Kovács László által összeállított kötetet. Ott, ahol vitatható értelmezéseket talál, szálljon vitába velük, és ott, ahol hiányoznak adatok, segítse lehetőségeihez képest a tudománytörténeti kutatásokat, ezzel is kiemelve Segner nemzetközi tudománytörténeti megítélésének elhanyagolt magyar vonatkozásait.

Hujter Mihály
matematikus, tudománytörténész,
BME Matematika Intézet
http://math.bme.hu/~hujter

Kovács László: Segner János András. Egy jeles hungarus a 18. századból. Orvos, matematikus, fizikus, csillagász, vegyész, tanár, filozófus és műszaki alkotó. Kiadó: Magyar Tudománytörténeti és Egészségtudományi Intézet. (Budapest. ISBN 978-615-5365-25-6.) http://real.mtak.hu/74845

Irodalomjegyzék

[1] Segner arcképe Reibenstein festménye részleteként: http://math.bme.hu/~hujter/segner.jpg

[2] Richard P. Stanley: Catalan Numbers http://www-math.mit.edu/~rstan

[3] Rab Irén: Hungarus-tudat és diákmentalitás a 18. századi göttingeni peregrinációban - különös tekintettel a medicinára - emlékkönyvek és egyéb peregrinációs források tükrében, Doktori értekezés, Semmelweis Egyetem, 2015. http://phd.semmelweis.hu/mwp/phd_live/vedes/export/rabiren.d.pdf

[4] Gazda István: A Segner-kötet bemutatása — 9 és fél perces videó, 2018. https://drive.google.com/open?id=1MBElpuOP8IKcSxQRx92mu_6xpcqpzzqy

Lábjegyzetek

¹ A szabatos megfogalmazásra érdemes felidézni Hajós György Elemi geometria c. alapművének 28.3 tételét, az itteni bizonyítás gyakorlatilag nem használ matematikai analízist. (A szerk.)

² Az, hogy ki találta fel a világon először a logarlécet, ma is vitatott kérdés. Már 1620 körül többféle eszközt készítettek. Segner találmánya Németországban lehetett egyik őse a mai logarlécnek. (A szerk.)