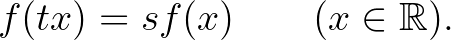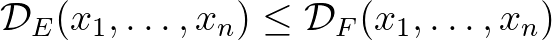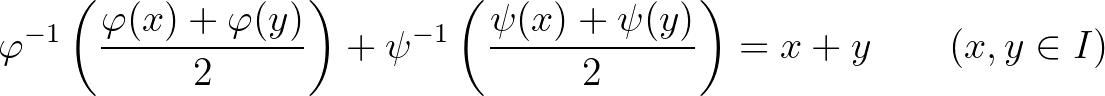Daróczy Zoltán élete
Daróczy Zoltán egy bihartordai jegyző második gyermekeként 1938-ban született. Református nevelést kapott és igen jól tanult, ezért szülei a Debreceni Református Kollégiumba küldték. Diákként kedvelte az irodalmat, a történelmet és a matematikát. „A matematika az nem más, mint szabatos beszéd.” – hallotta ezt gimnáziumi matematikatanárától, Nagy Gézától. Tanára hatására és biztatására részt vett az Arany Dániel matematikai versenyen és a KöMaL pontversenyében is. Talán ezek miatt választotta Daróczy Zoltán a tanári pályát, és felvételizett 1956-ban a Kossuth Lajos Tudományegyetem matematika-ábrázoló geometria szakára. Maximális pontszámmal is csak fellebbezés után vették fel. Alig kezdődött el az egyetemi oktatás, kitört az 56-os forradalom. Egyetemistaként a nemzetőrséghez csatlakozott, és így próbált tenni valamit az igaz ügyért. A forradalom leverését követően az oktatás csak 1957 tavaszán indult újra és mivel nem zárták ki az egyetemről, így 1961-ben kitüntetéses diplomával végezhetett. Jó tanárai voltak. A matematikai analízist, annak szépségét és szeretetét Rapcsák Andrástól és Aczél Jánostól tanulta. Hamar megértette a hangyabokányi epszilon fogalmát és később, amikor már ő állt a katedrán, tanárgenerációknak adta tovább, amit tanáraitól tanult: tudományt, műveltséget és emberséget. Daróczy Zoltán közel öt évtizeden keresztül volt a KLTE TTK matematika tanárszakos és matematikus hallgatóinak meghatározó és széles körben kedvelt oktatója. Előadásain diákjaival megszerettette a mértékelméletet és a valós függvénytant. Híresek voltak speciálkollégiumai, amelyeken hallgatóit eljuttatta az aktuális kutatási kérdésekig. Igazi reneszánsz ember volt, a tudományokat komplex módon oktatta, rávilágítva a tágabb összefüggésekre, de teret hagyva az önálló gondolkodásnak is.
Tanulmányai befejezése után nem kapott állást a Kossuth Lajos Tudományegyetemen, de az egyik első tudományos dolgozatában rámutatott Rényi Alfréd egy pontatlanságára. Ennek köszönhetően Rényi ösztöndíjasként felvette a Matematikai Kutatóintézetbe. Az itt töltött egy év alatt szerezte meg az egyetemi doktori fokozatot Aczél János irányítása mellett. 1963-tól egy évig a Bécsi Egyetem Matematikai Intézetének munkatársa volt Leopold Schmetterer meghívására. 1964-től dolgozott folyamatosan a KLTE-n, majd a jogutód Debreceni Egyetemen. 29 évesen a matematikai tudomány kandidátusa, 38 évesen a matematikai tudomány doktora lett és kinevezték egyetemi tanárnak. A Magyar Tudományos Akadémia 1985-ben levelező, 1990-ben pedig rendes tagjává választotta.
Az egyetem Analízis Tanszékének vezetését 1968-tól kezdve 16 éven át látta el. Pályája során 5 évig volt a Matematikai Intézet igazgatója, a Természettudományi Kar dékánhelyettese, majd dékánja. A rendszerváltást megelőző időszakban három–három évig volt az egyetem rektorhelyettese, majd rektora. Alapítója, majd 18 éven át vezetője volt a Debreceni Egyetem Matematika és Számítástudományok Doktori Iskolájának. 2008-ban, nyugdíjba vonulásakor, professor emeritusi címet kapott. Fiatalon a legfontosabb eredményeit az információelméletből származó függvényegyenletek vizsgálatában, a Shannon-entrópia karakterizációival kapcsolatban érte el. Az ezeket az eredményeket is bemutató, Aczél Jánossal közösen írt monográfiája a témakör legtöbbet idézett könyvévé vált. Jelentős a hozzájárulása a közepek elméletéhez is. Bevezette az eltérésközepek fogalmát, és alapvető eredményeket ért el a közepekre vonatkozó úgynevezett invariancia-egyenletek vizsgálatában.

1. ábra. Daróczy Zoltán (1938–2023)
Aczél János 1965-ben elhagyta Magyarországot, de a vele való baráti kapcsolata és együttműködése sohasem szakadt meg. Innen kezdve több mint ötven évig vezette, tanácsaival irányította a függvényegyenletek és egyenlőtlenségek kutatócsoportot, amely világszerte nagy elismerést szerzett. Lényeglátó képességének köszönhetően a hozzá közel álló kutatók, oktatók mindig a témakör legfontosabb kérdéseire koncentrálhattak. A kutatócsoport nemzetközi kapcsolatai a 70-es években kiszélesedtek, a csoport tagjai innentől kezdve számos fontos nyugati konferenciára kaptak meghívást. Emlékezetesek voltak az ezekre történő kiutazások, az együtt töltött idő és a nehézségeket is megkönnyítő, megértő jó természete. Témavezetése mellett 14 tanítványa (ld. Mathematical Geneaology) szerzett PhD fokozatot, akik többsége ma is aktív, nemzetközileg is elismert oktató- és kutatómunkát végez. Közülük Nagy Béla, Sebestyén Zoltán, Maksa Gyula, Járai Antal, Székelyhidi László, Páles Zsolt az MTA doktori címet is megszerezte. A saját sikereinél is fontosabbak voltak számára tanítványai sikerei. Mindent megtett az ő elismertetésük érdekében és aztán velük örült, ha ez bekövetkezett. Az is nagy örömére szolgált, hogy Bálint fia az ő nyomdokaiba lépett és a matematikusi életpályát választotta.
Az Analízis Tanszék életében fontos szerepet játszottak a tanszéki szemináriumok. Ezek egyik fontos változata a 80-as évek közepétől napjainkig évente megrendezett Síkfőkúti Analízis Szeminárium. Az ilyen összejöveteleken a tanszéki kollégák és a PhD hallgatók mellett azok családtagjai is részt vehettek. Ezek a rendezvények nagyban segítették az emberi, baráti kapcsolatok kialakulását. Daróczy Zoltán 40 éven keresztül családjával együtt szinte állandó résztvevője volt ezeknek az szemináriumoknak. A gyerekek, köztük Orsi és Bálint, együtt játszottak. Olyanok voltunk, és vagyunk ma is, mint egy nagy család. Zolinak, kortól függetlenül, mindenkihez volt egy kedves szava. Humora, empatikussága és tájékozottsága révén mindig a társaság középpontja volt.
Daróczy Zoltán már középiskolás korában elkezdett versenyszerűen sakkozni, egyetemi évei alatt pedig a DEAC sakkcsapatában játszott. A 70-es, 80-as években a mindig felállított sakktáblánál a TTK és BTK számos oktatója vívott schnell partikat vele és a tanszék tagjaival. Csak mostanra tudatosult bennünk, hogy milyen erős közösségformáló ereje volt ennek a tevékenységnek is.
Tudományos pályája mellett a politikai életben is aktívan részt vett. A 80-as évek végén csatlakozott a reformmozgalmakhoz, amelyek végül az egypártrendszer felbomlásához és a rendszerváltáshoz vezettek. Az 1990-es országgyűlési képviselőválasztáson a Magyar Szocialista Párt Hajdú-Bihar megyei területi listájáról, négy évvel később pedig az egyik debreceni egyéni körzetben szerzett mandátumot és lett parlamenti képviselő.
Daróczy Zoltán hazai elismertségét többek között az Akadémiai Díj, a Szele Tibor-emlékérem, a Szent-Györgyi Albert-díj, a Széchenyi-díj és a Magyar Köztársasági Érdemrend középkeresztje mutatja. Tudományos tevékenységét külföldön is felismerték: A világ egyik legrégebbi tudományos szervezete, a Hamburgi Matematikai Társaság 2008-ban tiszteletbeli tagjává választotta.
Tanítványaival, munkatársaival nemcsak szakmai, hanem bensőséges emberi kapcsolatokat ápolt. A vezetésére bízott közösségeket nagy empátiával, hozzáértéssel irányította, tanácsaival, szeretetével mindannyiunk életét segítette. Olvasottsága, műveltsége, nyitottsága és tájékozottsága példaértékű volt. Halálával a Debreceni Egyetem és a Magyar Tudományos Akadémia egy kiváló oktatóját, kutatóját és szellemi vezetőjét veszítette el.
Charles Dickens a „Karácsonyi ének”-ben ezt írja: „A végzet minden emberre kiszabta, hogy szellemével hasson embertársaira, környezetére.” Daróczy Zoltánról ezt biztosan elmondható.
Daróczy Zoltán tudományos eredményei
Az alábbiakban a célunk Daróczy Zoltán néhány alapvető és sokat idézett matematikai eredményének a bemutatása. Ennek a résznek a megírásakor felhasználtuk a szerző és Székelyhidi László [53] dolgozatát.
1. Additív függvények homogenitási tulajdonságai
Daróczy Zoltán egyik első tudományos dolgozata a szegedi Acta Sci. Math.-ban jelent meg és ebben a valós additív függvények homogenitási tulajdonságait tisztázta.
Egy 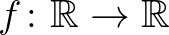 függvényt additívnak nevezünk, ha teljesíti az alábbi Cauchy-féle függvényegyenletet:
függvényt additívnak nevezünk, ha teljesíti az alábbi Cauchy-féle függvényegyenletet:
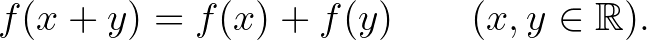
Az 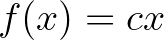 (ahol
(ahol 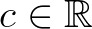 ) alakú függvények ennek a függvényegyenletnek a folytonos megoldásai. Hamel 1905-ös [39] dolgozatának köszönhetően tudjuk, hogy ennek az egyenletnek vannak nem folytonos megoldásai is, sőt véve a valós számoknak mint egy a racionális számok teste feletti vektortérnek egy tetszőleges (Hamel) bázisát, bármely ezen a bázison értelmezett valós értékű függvény egyértelműen kiterjeszthető
) alakú függvények ennek a függvényegyenletnek a folytonos megoldásai. Hamel 1905-ös [39] dolgozatának köszönhetően tudjuk, hogy ennek az egyenletnek vannak nem folytonos megoldásai is, sőt véve a valós számoknak mint egy a racionális számok teste feletti vektortérnek egy tetszőleges (Hamel) bázisát, bármely ezen a bázison értelmezett valós értékű függvény egyértelműen kiterjeszthető 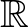 -re egy additív függvénnyé.
-re egy additív függvénnyé.
Jól ismert (és nem is nehéz igazolni azt), hogy minden additív függvény 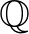 -homogén, azaz minden
-homogén, azaz minden 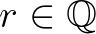 esetén teljesül
esetén teljesül
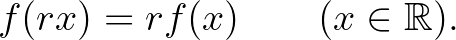
Folytonos additív függvények esetén ez az egyenlőség minden 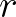 valós számra is fennáll. Természetesnek tűnő probléma tehát az, hogy milyen
valós számra is fennáll. Természetesnek tűnő probléma tehát az, hogy milyen 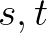 irracionális számok esetén van olyan
irracionális számok esetén van olyan 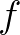 nem azonosan nulla additív függvény, amelyre teljesül
nem azonosan nulla additív függvény, amelyre teljesül
Daróczy Zoltán [9] alábbi eredménye ezt a kérdést teljesen megválaszolja.
1.1. tétel. Ha 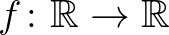 egy olyan nem azonosan nulla additív függvény, amelyre teljesül (1) valamilyen
egy olyan nem azonosan nulla additív függvény, amelyre teljesül (1) valamilyen 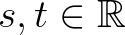 irracionális számpárra, akkor vagy
irracionális számpárra, akkor vagy 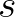 és
és 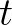 algebraiak és egymás algebrai konjugáltjai (azaz közös a definiáló polinomjuk), vagy
algebraiak és egymás algebrai konjugáltjai (azaz közös a definiáló polinomjuk), vagy 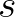 és
és 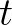 transzcendens.
transzcendens.
2. Kiterjesztési tételek
A függvényegyenletek megoldása során nagyon sokszor áll elő az a helyzet, amikor egy valós függvényről az additivitást csak a számpároknak egy részhalmazán lehet igazolni. Az alapkérdés, hogy ilyenkor a függvény milyen közel áll az additív függvényekhez. Ezen a területen Aczél János és Erdős Pál [2] érte el az első eredményt.
2.1. tétel. Legyen 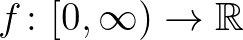 egy olyan függvény, amelyre
egy olyan függvény, amelyre 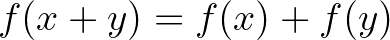 teljesül minden
teljesül minden 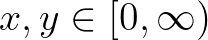 esetén. Ekkor
esetén. Ekkor 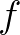 egyértelműen terjeszthető ki
egyértelműen terjeszthető ki 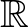 -re egy additív függvénnyé, azaz van egy olyan egyértelműen meghatározott
-re egy additív függvénnyé, azaz van egy olyan egyértelműen meghatározott 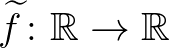 additív függvény, hogy
additív függvény, hogy 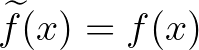 minden
minden 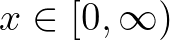 esetén.
esetén.
A másik alapvető kiterjesztési tételt Daróczy Zoltán és Losonczi László [23] találta meg.
2.2. tétel. Legyen ![$f\colon [0,1]\to\mathbb{R}$](/images/stories/latexuj/2023-11/2023-11-paleszsoltdaroczyzolta85/img22.png) egy olyan függvény, amelyre
egy olyan függvény, amelyre 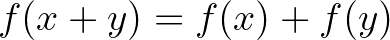 teljesül minden olyan
teljesül minden olyan ![$x,y\in[0,1]$](/images/stories/latexuj/2023-11/2023-11-paleszsoltdaroczyzolta85/img23.png) esetén, amelyre
esetén, amelyre 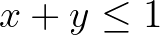 . Ekkor
. Ekkor 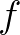 egyértelműen terjeszthető ki
egyértelműen terjeszthető ki 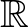 -re egy additív függvénnyé, azaz van egy olyan egyértelműen meghatározott
-re egy additív függvénnyé, azaz van egy olyan egyértelműen meghatározott 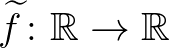 additív függvény, hogy
additív függvény, hogy 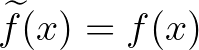 minden
minden ![$x\in[0,1]$](/images/stories/latexuj/2023-11/2023-11-paleszsoltdaroczyzolta85/img25.png) esetén.
esetén.
Ezek az eredmények számos további vizsgálatot indukáltak és a függvényegyenletek megoldásának a mai napig az alapvető eszközei. A teljesség igénye nélkül az olvasó figyelmét a következő dolgozatokra hívjuk fel: [3, 25, 43, 44, 52, 55, 58].
3. Információfüggvények jellemzése
A 60-as–70-es években az információelmélet a függvényegyenletek elmélete számára számos érdekes és mély problémát szolgáltatott. Aczél János és Daróczy Zoltán 1975-ben publikált [1] monográfiája az ezen a területen elért legfontosabb eredményeket foglalta össze. Az alábbiakban az információfüggvényekkel kapcsolatosan elért eredményekből válogatunk.
Legyen 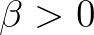 egy rögzített konstans. Egy
egy rögzített konstans. Egy ![$f\colon [0,1]\to\mathbb{R}$](/images/stories/latexuj/2023-11/2023-11-paleszsoltdaroczyzolta85/img22.png) leképezést
leképezést 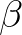 -típusú információfüggvénynek nevezünk, ha
-típusú információfüggvénynek nevezünk, ha 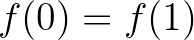 ,
, 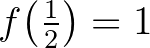 , és minden olyan
, és minden olyan  -ra, amelyre
-ra, amelyre 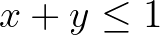 , fennáll az
, fennáll az
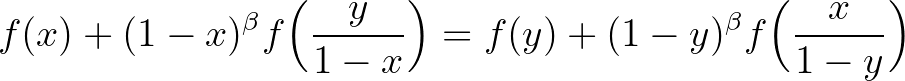
egyenlet. Ha 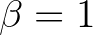 , akkor
, akkor 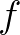 -et közönséges információfüggvénynek mondjuk.
-et közönséges információfüggvénynek mondjuk.
A 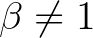 esetben a fenti függvényegyenlet a megadott mellékfeltételek mellett megoldható, és a következő eredmény igazolható [11]:
esetben a fenti függvényegyenlet a megadott mellékfeltételek mellett megoldható, és a következő eredmény igazolható [11]:
3.1. tétel. Ha 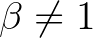 , akkor
, akkor ![$f\colon [0,1]\to\mathbb{R}$](/images/stories/latexuj/2023-11/2023-11-paleszsoltdaroczyzolta85/img22.png) pontosan akkor
pontosan akkor 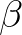 -típusú információfüggvény, ha
-típusú információfüggvény, ha
![$\displaystyle f(x)={\frac1{2^{1-\beta}-1}}\big(x^{\beta}+(1-x)^{\beta}-1\big)\qquad(x\in[0,1]).
$](/images/stories/latexuj/2023-11/2023-11-paleszsoltdaroczyzolta85/img35.png)
Tehát 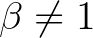 esetén a
esetén a 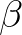 -típusú információfüggvények egyértelműen meghatározottak és folytonosak. Ha képezzük a
-típusú információfüggvények egyértelműen meghatározottak és folytonosak. Ha képezzük a  határátmenetet, akkor eredményül az
határátmenetet, akkor eredményül az
![$\displaystyle S(x):=-x\log_2x-(1-x)\log_2(1-x) \qquad(x\in[0,1])
$](/images/stories/latexuj/2023-11/2023-11-paleszsoltdaroczyzolta85/img37.png)
képlettel megadható függvényt kapjuk, amit Shannon-féle információfüggvénynek nevezünk (itt a 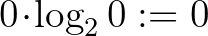 konvencióval élünk). Az könnyen látható, hogy a Shannon-függvény
konvencióval élünk). Az könnyen látható, hogy a Shannon-függvény 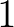 -típusú információfüggvény, azaz minden olyan
-típusú információfüggvény, azaz minden olyan  -ra, amelyre
-ra, amelyre 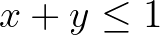 , teljesül az
, teljesül az
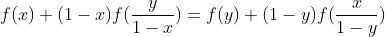
függvényegyenlet.
Az információfüggvényekkel kapcsolatban természetes feltétel a nemnegativitásuk. A Shannon-függvény triviálisan ilyen, de nem nyilvánvaló, hogy van-e más nemnegatív információfüggvény. A következő eredményt Daróczy Zoltán Kátai Imrével [14] együtt találta.
3.2. tétel. Ha ![$f\colon [0,1]\to\mathbb{R}$](/images/stories/latexuj/2023-11/2023-11-paleszsoltdaroczyzolta85/img22.png) egy korlátos és nemnegatív információfüggvény, akkor
egy korlátos és nemnegatív információfüggvény, akkor 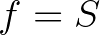 .
.
Ha a korlátosság feltételét elhagyjuk, akkor a helyzet gyökeresen megváltozik. Ezt Daróczy Zoltán és Maksa Gyula [24] alábbi eredménye mutatja.
3.3. tétel. Ha ![$f\colon [0,1]\to\mathbb{R}$](/images/stories/latexuj/2023-11/2023-11-paleszsoltdaroczyzolta85/img22.png) egy nemnegatív információfüggvény, akkor
egy nemnegatív információfüggvény, akkor 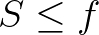 . Továbbá léteznek a Shannon-függvénytől különböző nemnegatív információfüggvények.
. Továbbá léteznek a Shannon-függvénytől különböző nemnegatív információfüggvények.
4. A természetes számok homomorfizmusai kompakt Abel-csoportokba
Daróczy Zoltánnak és Kátai Imrének az egyik fontos közös kutatási területe volt az additív számelméleti függvények aszimptotikus tulajdonságainak a vizsgálata. Ebből az együttműködésükből több mint 10 közös dolgozatuk született. A [15] dolgozat egyik főeredménye az alábbi
4.1. tétel. Legyen 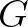 egy kompakt Abel-csoport és legyen
egy kompakt Abel-csoport és legyen 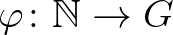 egy additív függvény. Ekkor
egy additív függvény. Ekkor 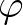 pontosan akkor teljesíti a
pontosan akkor teljesíti a
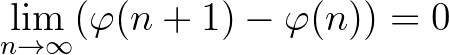
egyenlőséget, ha minden olyan 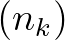 olyan növekvő természetes számsorozat esetén, amelyre a
olyan növekvő természetes számsorozat esetén, amelyre a 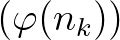 sorozat konvergens, konvergens a
sorozat konvergens, konvergens a 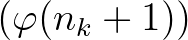 sorozat is.
sorozat is.
A direkt implikáció azonnal látható. A fordított irányú implikáció igazolásához viszont nem triviális ötletre van szükség.
Ez az eredmény Daróczy Zoltán és Kátai Imre számos további közös dolgozatának volt a kiindulópontja. A teljesség igénye nélkül csak a következő cikkeket említjük meg: [16, 17, 18, 19, 20, 21, 22].
5. Közepek homogenitása
Az entrópia fogalmak axiomatikus vizsgálata során Rényi Alfréd az alábbi fogalmat vezette be: Ha adott egy 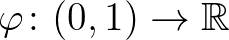 folytonos és szigorúan monoton függvény, akkor értelmezzük az
folytonos és szigorúan monoton függvény, akkor értelmezzük az
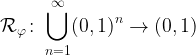
közepet az alábbi képlettel:
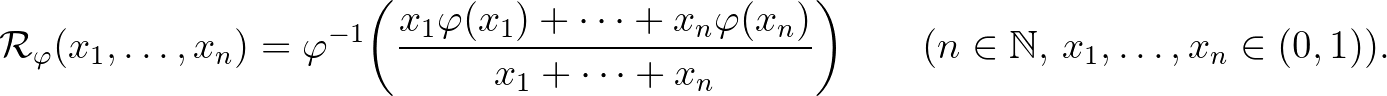
Rényi azt sejtette, hogyha ez a közép a nemteljes valószínűségeloszlások halmazán homogén, akkor 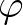 vagy a logaritmus függvényhez, vagy egy hatványfüggvényhez hasonló. A sejtést Daróczy Zoltán [10] igazolta az alábbi eredményében.
vagy a logaritmus függvényhez, vagy egy hatványfüggvényhez hasonló. A sejtést Daróczy Zoltán [10] igazolta az alábbi eredményében.
5.1. tétel. Legyen 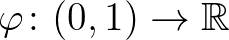 folytonos és szigorúan monoton függvény. Ha
folytonos és szigorúan monoton függvény. Ha
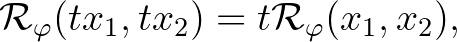
teljesül minden olyan 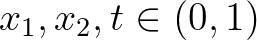 esetén, amelyre
esetén, amelyre 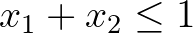 , akkor léteznek olyan
, akkor léteznek olyan 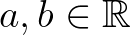 konstansok, hogy vagy
konstansok, hogy vagy 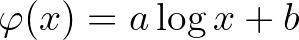 , vagy pedig
, vagy pedig 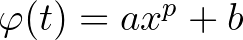 teljesül minden
teljesül minden 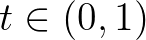 esetén valamilyen
esetén valamilyen 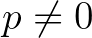 konstanssal.
konstanssal.
A Rényi által vizsgált közepekről kiderült, hogy egy a Bajraktarević [4, 5] által bevezetett középosztálynak egy részosztályát alkotják. Legyen 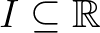 egy (nemdegenerált) intervallum, és legyenek
egy (nemdegenerált) intervallum, és legyenek 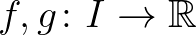 olyan függvények, hogy
olyan függvények, hogy 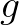 pozitív és az
pozitív és az 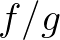 hányadosfüggvény szigorúan monoton és folytonos. Ekkor értelmezzük a
hányadosfüggvény szigorúan monoton és folytonos. Ekkor értelmezzük a 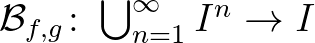 közepet az alábbi képlettel:
közepet az alábbi képlettel:

Ha 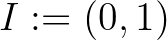 ,
, 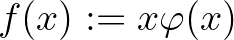 és
és 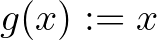 , akkor
, akkor 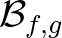 egyenlő a fentebb bevezetett Rényi-féle
egyenlő a fentebb bevezetett Rényi-féle 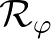 középpel. Ha pedig
középpel. Ha pedig 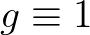 , akkor látható, hogy
, akkor látható, hogy 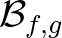 egy úgynevezett kváziaritmetikai középre egyszerűsödik.
egy úgynevezett kváziaritmetikai középre egyszerűsödik.
A Bajraktarević-közepek homogenitásának szükséges és elegendő feltételét Aczél János és Daróczy Zoltán az alábbi tételben írták le:
5.2. tétel. Legyenek 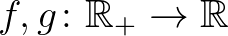 olyan folytonos függvények, hogy
olyan folytonos függvények, hogy 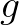 pozitív és
pozitív és 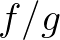 szigorúan monoton. Ekkor a
szigorúan monoton. Ekkor a 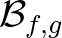 közép pontosan akkor homogén, azaz teljesül rá a
közép pontosan akkor homogén, azaz teljesül rá a
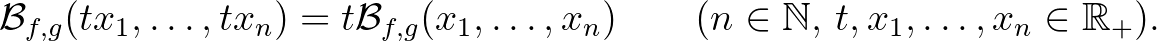
függvényegyenlet, ha léteznek olyan 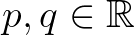 számok, hogy
számok, hogy 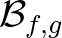 egyenlő a
egyenlő a
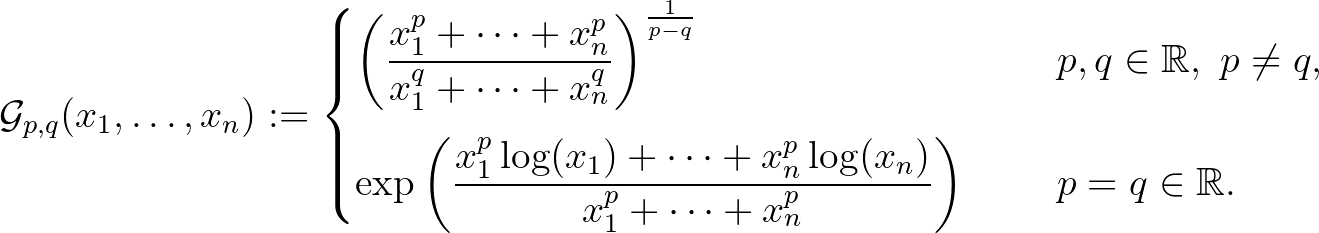
képlettel értelmezett 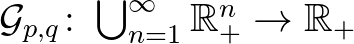 Gini-középpel.
Gini-középpel.
Megjegyezzük, hogy az [1] cikkben található tétel arra az esetre is kiterjed, amikor a 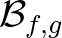 közép a pozitív valós számok halmazának csak egy valódi részintervallumán van értelmezve, és ekkor a jellemzésben a Gini-közepek konjugált komplex
közép a pozitív valós számok halmazának csak egy valódi részintervallumán van értelmezve, és ekkor a jellemzésben a Gini-közepek konjugált komplex 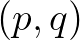 párokra vonatkozó kiterjesztései is fellépnek.
párokra vonatkozó kiterjesztései is fellépnek.
6. Eltérésközepek és egyenlőtlenségek
Daróczy Zoltán 1971-72-ben megjelent [12, 13] dolgozataiban a közepek egy olyan új osztályát vezette be, amely az addig ismert legfontosabb középosztályokat speciális esetként tartalmazta. Legyen 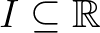 egy nemelfajuló nyílt intervallum. Egy olyan kétváltozós
egy nemelfajuló nyílt intervallum. Egy olyan kétváltozós 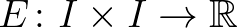 függvényt, amely a második változójában folytonos és szigorúan monoton csökkenő, továbbá eltűnik a diagonális elempárokon (azaz
függvényt, amely a második változójában folytonos és szigorúan monoton csökkenő, továbbá eltűnik a diagonális elempárokon (azaz 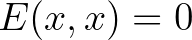 minden
minden 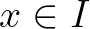 esetén), eltérésfüggvénynek nevezünk. Ekkor nem nehéz belátni, hogy minden
esetén), eltérésfüggvénynek nevezünk. Ekkor nem nehéz belátni, hogy minden 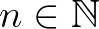 és
és 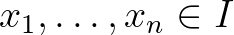 esetén az
esetén az
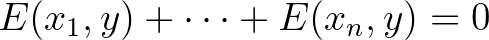
egyenletnek pontosan egy 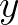 megoldása van
megoldása van 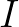 -ben és ez
-ben és ez 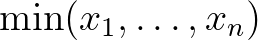 és
és 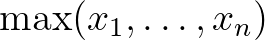 közé esik. Ezt az egyértelműen meghatározott
közé esik. Ezt az egyértelműen meghatározott 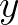 megoldást az
megoldást az 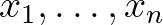 számok
számok 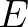 -eltérésközepének (vagy Daróczy-közepének) nevezzük és
-eltérésközepének (vagy Daróczy-közepének) nevezzük és 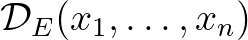 -vel jelöljük.
-vel jelöljük.
Könnyű belátni, hogy az 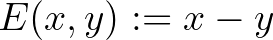 függvény eltérésfüggvény, és hogy az általa meghatározott közép a számtani közép. A geometriai közép, a harmonikus közép, általánosabban a hatványközepek, a kváziaritmetikai közepek, a Gini-közepek és a Bajraktarević-közepek az eltérésközepek részosztályait alkotják. A közöttük fennálló tartalmazásokat az alábbi diagram szemlélteti.
függvény eltérésfüggvény, és hogy az általa meghatározott közép a számtani közép. A geometriai közép, a harmonikus közép, általánosabban a hatványközepek, a kváziaritmetikai közepek, a Gini-közepek és a Bajraktarević-közepek az eltérésközepek részosztályait alkotják. A közöttük fennálló tartalmazásokat az alábbi diagram szemlélteti.
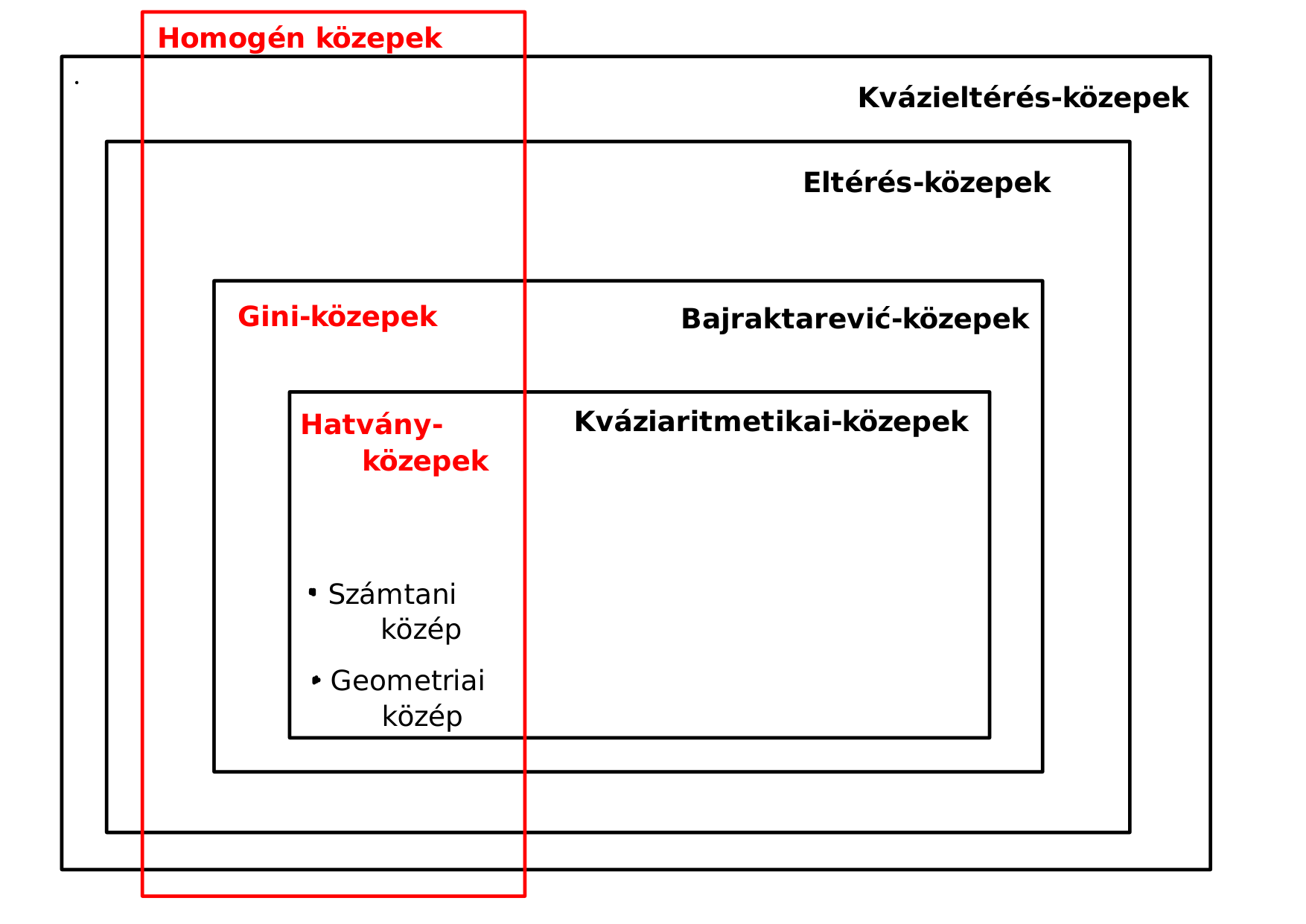
2. ábra. Közepek
Az eltérésközepekkel kapcsolatos legalapvetőbb probléma az egyenlőség, illetve az összehasonlíthatóság kérdése. De amint látni fogjuk, a Hölder- és Minkowski-típusú egyenlőtlenségek teljesülését is jellemezhetjük. A Daróczy Zoltán által talált eredmények megfogalmazásához valamelyest szűkítjük az eltérésfüggvények osztályát. Azt mondjuk, hogy egy 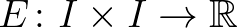 eltérésfüggvény reguláris, ha a második változója szerint differenciálható minden diagonális pontban, és itt a második változó szerinti parciális derivált negatív. Ha
eltérésfüggvény reguláris, ha a második változója szerint differenciálható minden diagonális pontban, és itt a második változó szerinti parciális derivált negatív. Ha 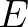 egy reguláris eltérésfüggvény, akkor az
egy reguláris eltérésfüggvény, akkor az 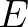 regularizáltján az alábbiak szerint megadott
regularizáltján az alábbiak szerint megadott 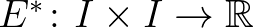 függvényt értjük:
függvényt értjük:
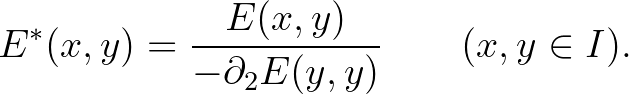
A fenti jelölések birtokában kimondhatjuk az alábbi tételt, ami a [12] dolgozatból származik.
6.1. tétel. Legyenek 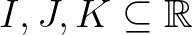 nemüres nyílt intervallumok és
nemüres nyílt intervallumok és 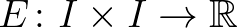 ,
, 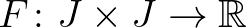 ,
, 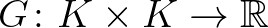 reguláris eltérésfüggvények és
reguláris eltérésfüggvények és 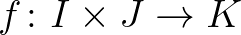 egy differenciálható függvény. Ekkor a
egy differenciálható függvény. Ekkor a
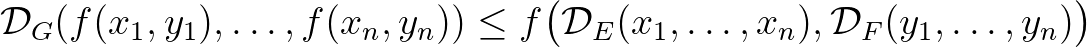
egyenlőtlenség akkor és csak akkor teljesül minden 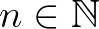 ,
, 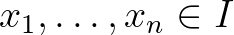 és
és 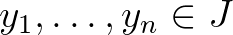 esetén, ha
esetén, ha
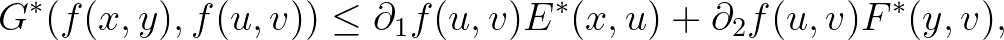
érvényes minden 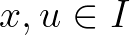 -re és
-re és 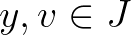 -re.
-re.
Ebből a tételből a Minkowski- és Hölder-típusú egyenlőtlenségek fennállásának szükséges és elegendő feltételeihez lehet jutni az 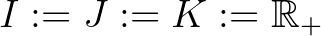 és
és 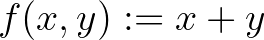 , illetve
, illetve 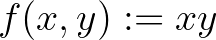 választásokkal. Ha a fenti tételt az
választásokkal. Ha a fenti tételt az 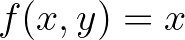 függvényre alkalmazzuk, akkor a [13] dolgozatban igazolt összehasonlítási tételt kapjuk.
függvényre alkalmazzuk, akkor a [13] dolgozatban igazolt összehasonlítási tételt kapjuk.
6.2. tétel. Legyen 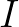 egy nemüres nyílt intervallum és
egy nemüres nyílt intervallum és 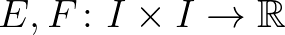 reguláris eltérésfüggvények. Ekkor a
reguláris eltérésfüggvények. Ekkor a
egyenlőtlenség akkor és csak akkor teljesül minden 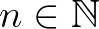 és
és 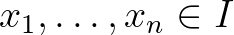 esetén, ha
esetén, ha
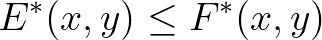
érvényes minden 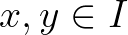 -re.
-re.
A Daróczy Zoltánnal közös [29] dolgozatunkban sikerült az összehasonlítási tételt az eltérésfüggvények regularitásának feltétele nélkül is megtalálni.
6.3. tétel. Legyenek 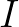 egy nemüres nyílt intervallum és
egy nemüres nyílt intervallum és 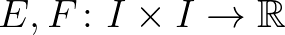 eltérésfüggvények. Ekkor a (2) egyenlőtlenség akkor és csak akkor teljesül minden
eltérésfüggvények. Ekkor a (2) egyenlőtlenség akkor és csak akkor teljesül minden 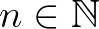 és
és 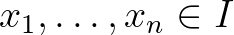 esetén, ha létezik egy olyan
esetén, ha létezik egy olyan 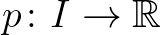 pozitív függvény, hogy
pozitív függvény, hogy
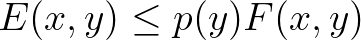
érvényes minden 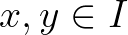 -re.
-re.
Az eltérésközepeknek számos általánosítása, alkalmazása található például a következő dolgozatokban: [7, 8, 30, 31, 47, 48, 49, 50, 51]
7. Invarianciaegyenlet kváziaritmetikai közepekkel
Legyen 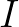 egy nemüres nyílt intervallum. Ha
egy nemüres nyílt intervallum. Ha 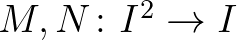 kétváltozós közepek, akkor tetszőleges
kétváltozós közepek, akkor tetszőleges 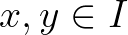 esetén tekintsük az
esetén tekintsük az
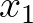 |
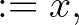 |
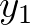 |
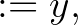 |
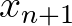 |
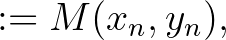 |
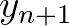 |
 |
képletekkel megadott Gauss-típusú iterációt. Feltételezve, hogy 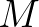 és
és 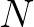 folytonos és szigorú közepek belátható, hogy az
folytonos és szigorú közepek belátható, hogy az 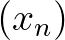 és
és 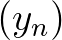 sorozatok egy közös
sorozatok egy közös 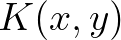 határértékhez konvergálnak. Ez az eljárás egy olyan
határértékhez konvergálnak. Ez az eljárás egy olyan 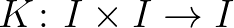 kétváltozós közepet határoz meg, amely a
kétváltozós közepet határoz meg, amely a
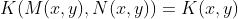
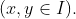
függvényegyenlet egyértelműen meghatározott megoldása. Ezt az egyenletet az 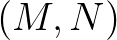 párra vonatkozó invarianciaegyenletnek nevezzük, és az ezt kielégítő
párra vonatkozó invarianciaegyenletnek nevezzük, és az ezt kielégítő 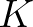 közepet pedig egy
közepet pedig egy 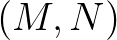 -invariáns középnek mondjuk. Egy egyszerű példa az invarianciaegyenletre az alábbi azonosság
-invariáns középnek mondjuk. Egy egyszerű példa az invarianciaegyenletre az alábbi azonosság
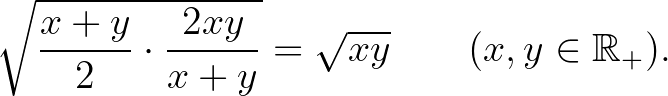
ami azt mutatja, hogy a kétváltozós geometriai közép invariáns a kétváltozós számtani és harmonikus közepekre nézve.
Carl Friedrich Gaussnak a számtani-geometriai középpel kapcsolatos alapvető eredménye [37] így fogalmazható:
7.1. tétel. Egy folytonos 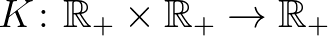 közép pontosan akkor megoldása a
közép pontosan akkor megoldása a
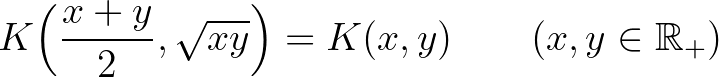
egyenletnek, ha
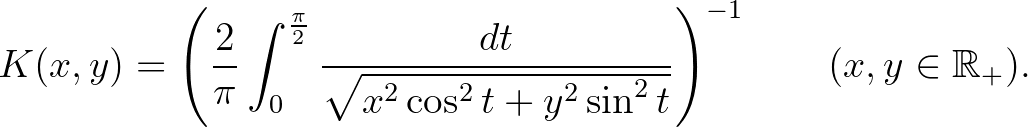
A [35] dolgozat célkitűzése az olyan kétváltozós kváziaritmetikai középpárok meghatározása, amelyekhez tartozó invariáns közép szintén kváziaritmetikai. Ez a probléma könnyen kitalálható helyettesítések után arra a speciális esetre redukálható, amikor az invariáns közép a kétváltozós számtani közép. Tehát a feladat az olyan 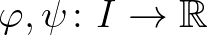 folytonos és szigorúan monoton függvények meghatározása, amelyek teljesítik a
folytonos és szigorúan monoton függvények meghatározása, amelyek teljesítik a
függvényegyenletet. Ezt az egyenletet O. Sutô [56, 57] 1914-ben megjelent dolgozataiban az analitikus függvények körében vizsgálta és meghatározta megoldásait. Janusz Matkowski [45] 1999-ben kétszeri folytonos differenciálhatóság feltételezése mellett igazolta, hogy a fenti egyenletnek a megoldásai változatlanok. A probléma természetes regularitási feltételek melletti megoldását a [35] (magyar nyelven a [32]) dolgozatunkban adtuk meg.
7.2. tétel. Legyenek 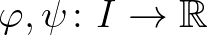 folytonos és szigorúan monoton függvények. Ekkor a (3) invarianciaegyenlet akkor és csak akkor teljesül a
folytonos és szigorúan monoton függvények. Ekkor a (3) invarianciaegyenlet akkor és csak akkor teljesül a 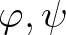 függvényekre, ha léteznek olyan
függvényekre, ha léteznek olyan 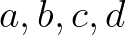 valós konstansok, hogy
valós konstansok, hogy 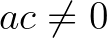 és vagy
és vagy 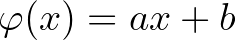 és
és 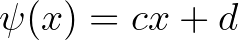 teljesül minden
teljesül minden 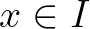 esetén, vagy pedig létezik egy olyan
esetén, vagy pedig létezik egy olyan 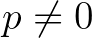 valós konstans, hogy fennáll
valós konstans, hogy fennáll 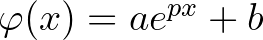 és
és 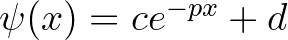 , ha
, ha 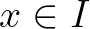 .
.
A tétel bizonyításának lényege annak kimutatása volt, hogy a (3) invarianciaegyenlet fennállásából a 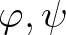 függvények kétszeri differenciálhatósága következik. Ehhez többek között Lebesgue-nek a monoton függvények majdnem mindenütti differenciálhatóságára vonatkozó tételét, vagy Baire-nek a deriválfüggények folytonossági helyeinek a sűrűségére vonatkozó tételét is fel kellett használni. A további részletek a [35], illetve a [32] dolgozatokban találhatók meg. A témakörrel kapcsolatos további eredmények születtek még a következő cikkekben: [6, 26, 27, 28, 32, 33, 34, 36, 38, 40, 41, 42, 46, 54].
függvények kétszeri differenciálhatósága következik. Ehhez többek között Lebesgue-nek a monoton függvények majdnem mindenütti differenciálhatóságára vonatkozó tételét, vagy Baire-nek a deriválfüggények folytonossági helyeinek a sűrűségére vonatkozó tételét is fel kellett használni. A további részletek a [35], illetve a [32] dolgozatokban találhatók meg. A témakörrel kapcsolatos további eredmények születtek még a következő cikkekben: [6, 26, 27, 28, 32, 33, 34, 36, 38, 40, 41, 42, 46, 54].
Páles Zsolt
Debreceni Egyetem, Matematikai Intézet
Irodalomjegyzék
- [1] J. Aczél and Z. Daróczy. On Measures of Information and Their Characterizations. Academic Press [Harcourt Brace Jovanovich Publishers], New York, 1975. Mathematics in Science and Engineering, Vol. 115.
[2] J. Aczél and P. Erdős. The nonexistence of a Hamel-basis and the general solution of Cauchy's functional equation for nonnegative numbers. Publ. Math. Debrecen, 12:253–263, 1965.
[3] J. Aczél and L. Losonczi. Extension of functional equations. In The mathematics of Paul Erdős, II, page 251–263. Springer, Berlin, 1997.
[4] M. Bajraktarević. Sur une équation fonctionnelle aux valeurs moyennes. Glasnik Mat.-Fiz. Astronom. Društvo Mat. Fiz. Hrvatske Ser. II, 13:243–248, 1958.
[5] M. Bajraktarević. Sur une généralisation des moyennes quasilinéaires. Publ. Inst. Math. (Beograd) (N.S.), 3 (17):69–76, 1963.
[6] P. Burai. Matkowski–Sutô type equation on symmetrized weighted quasi-arithmetic means. Results Math., 63(1-2):397–408, 2013.
[7] J. Chudziak. On applications of inequalities for quasideviation means in actuarial mathematics. Math. Inequal. Appl., 21(3):601–610, 2018.
[8] J. Chudziak and M. Chudziak. On some applications of quasideviation means. J. Difference Equ. Appl., 25(9-10):1429–1437, 2019.
[9] Z. Daróczy. Notwendige und hinreichende Bedingungen für die Existenz von nichtkonstanten Lösungen linearer Funktionalgleichungen. Acta Sci. Math. (Szeged), 22:31–41, 1961.
[10] Z. Daróczy. Über die gemeinsame Charakterisierung der zu den nicht vollständigen Verteilungen gehörigen Entropien von Shannon und von Rényi. Z. Wahrscheinlichkeitstheorie und Verw. Gebiete, 1:381–388, 1962.
[11] Z. Daróczy. Generalized information functions. Information and Control, 16:36–51, 1970.
[12] Z. Daróczy. A general inequality for means. Aequationes Math., 7(1):16–21, 1971.
[13] Z. Daróczy. Über eine Klasse von Mittelwerten. Publ. Math. Debrecen, 19:211–217 (1973), 1972.
[14] Z. Daróczy and I. Kátai. Additive zahlentheoretische Funktionen und das Mass der Information. Ann. Univ. Sci. Budapest. Eötvös Sect. Math., 13:83–88 (1971), 1970.
[15] Z. Daróczy and I. Kátai. On additive number-theoretical functions with values in a compact Abelian group. Aequationes Math., 28(3):288–292, 1985.
[16] Z. Daróczy and I. Kátai. Additive functions. Anal. Math., 12(2):85–96, 1986.
[17] Z. Daróczy and I. Kátai. On additive arithmetical functions with values in topological groups. I. Publ. Math. Debrecen, 33(3-4):287–291, 1986.
[18] Z. Daróczy and I. Kátai. On additive arithmetical functions with values in the circle group. Publ. Math. Debrecen, 34(3-4):307–312, 1987.
[19] Z. Daróczy and I. Kátai. On additive arithmetical functions with values in topological groups. II. Publ. Math. Debrecen, 34(1-2):65–68, 1987.
[20] Z. Daróczy and I. Kátai. Characterization of additive functions with values in the circle group. Publ. Math. Debrecen, 36(1-4):1–7 (1990), 1989.
[21] Z. Daróczy and I. Kátai. On additive functions taking values from a compact group. Acta Sci. Math. (Szeged), 53(1-2):59–65, 1989.
[22] Z. Daróczy and I. Kátai. Characterization of additive functions with values in the circle group. II. Publ. Math. Debrecen, 44(3-4):391–394, 1994.
[23] Z. Daróczy and L. Losonczi. Über die Erweiterung der auf einer Punktmenge additiven Funktionen. Publ. Math. Debrecen, 14:239–245, 1967.
[24] Z. Daróczy and Gy. Maksa. Nonnegative information functions. In Analytic function methods in probability theory (Proc. Colloq. Methods of Complex Anal. in the Theory of Probab. and Statist., Lajos Kossuth Univ. Debrecen, Debrecen, 1977), page 67–78. North-Holland, Amsterdam, 1979.
[25] Z. Daróczy and Gy. Maksa. Functional equations on convex sets. Acta Math. Hungar., 68(3):187–195, 1995.
[26] Z. Daróczy and Gy. Maksa. On a problem of Matkowski. Colloq. Math., 82(1):117–123, 1999.
[27] Z. Daróczy, Gy. Maksa, and Zs. Páles. Extension theorems for the Matkowski–Sutô problem. Demonstratio Math., 33(3):547–556, 2000.
[28] Z. Daróczy, Gy. Maksa, and Zs. Páles. Functional equations involving means and their Gauss composition. Proc. Amer. Math. Soc., 134(2):521–530, 2006.
[29] Z. Daróczy and Zs. Páles. On comparison of mean values. Publ. Math. Debrecen, 29(1-2):107–115, 1982.
[30] Z. Daróczy and Zs. Páles. Multiplicative mean values and entropies. In Functions, series, operators, Vol. I, II (Budapest, 1980), page 343–359. North-Holland, Amsterdam, 1983.
[31] Z. Daróczy and Zs. Páles. Generalized-homogeneous deviation means. Publ. Math. Debrecen, 33(1-2):53–65, 1986.
[32] Z. Daróczy and Zs. Páles. Középértékek Gauss-féle kompozíciója és a Matkowski–Sutô probléma megoldása. Mat. Lapok (N.S.), 8/9(3-4):1–53, 1998/99 (2003).
[33] Z. Daróczy and Zs. Páles. On means that are both quasi-arithmetic and conjugate arithmetic. Acta Math. Hungar., 90(4):271–282, 2001.
[34] Z. Daróczy and Zs. Páles. A Matkowski–Sutô type problem for quasi-arithmetic means of order 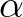 . In Z. Daróczy and Zs. Páles, editors, Functional Equations — Results and Advances, volume 3 of Adv. Math. (Dordr.), page 189–200. Kluwer Acad. Publ., Dordrecht, 2002.
. In Z. Daróczy and Zs. Páles, editors, Functional Equations — Results and Advances, volume 3 of Adv. Math. (Dordr.), page 189–200. Kluwer Acad. Publ., Dordrecht, 2002.
[35] Z. Daróczy and Zs. Páles. Gauss-composition of means and the solution of the Matkowski–Sutô problem. Publ. Math. Debrecen, 61(1-2):157–218, 2002.
[36] Z. Daróczy and Zs. Páles. A Matkowski–Sutô-type problem for weighted quasi-arithmetic means. Ann. Univ. Sci. Budapest. Sect. Comput., 22:69–81, 2003.
[37] C. F. Gauss. Bestimmung der Anziehung eines elliptischen Ringes. Akademische Verlagsgesellschaft M. B. H., Leipzig, 1927. Nachlass zur Theorie des arithmetisch-geometrischen Mittels und der Modulfunktion.
[38] R. Grünwald and Zs. Páles. On the invariance of the arithmetic mean with respect to generalized Bajraktarević means. Acta Math. Hungar., 166(2):594–613, 2022.
[39] G. Hamel. Eine Basis aller Zahlen und die unstetigen Lösungen der Funktionalgleichung 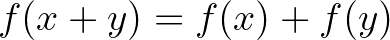 . Math. Ann., 60:459–462, 1905.
. Math. Ann., 60:459–462, 1905.
[40] J. Jarczyk. Invariance of weighted quasi-arithmetic means with continuous generators. Publ. Math. Debrecen, 71(3-4):279–294, 2007.
[41] J. Jarczyk. Invariance of quasi-arithmetic means with function weights. J. Math. Anal. Appl., 353(1):134–140, 2009.
[42] J. Jarczyk and J. Matkowski. Invariance in the class of weighted quasi-arithmetic means. Ann. Polon. Math., 88(1):39–51, 2006.
[43] K. Lajkó. Applications of extensions of additive functions. Aequationes Math., 11:68–76, 1974.
[44] L. Losonczi. An extension theorem. Aequationes Math., 28(3):293–299, 1985.
[45] J. Matkowski. Invariant and complementary quasi-arithmetic means. Aequationes Math., 57(1):87–107, 1999.
[46] J. Matkowski and Zs. Páles. Characterization of generalized quasi-arithmetic means. Acta Sci. Math. (Szeged), 81(3-4):447–456, 2015.
[47] Zs. Páles. Characterization of quasideviation means. Acta Math. Acad. Sci. Hungar., 40(3-4):243–260, 1982.
[48] Zs. Páles. Ingham Jessen's inequality for deviation means. Acta Sci. Math. (Szeged), 49(1-4):131–142, 1985.
[49] Zs. Páles. General inequalities for quasideviation means. Aequationes Math., 36(1):32–56, 1988.
[50] Zs. Páles. On a Pexider-type functional equation for quasideviation means. Acta Math. Hungar., 51(1-2):205–224, 1988.
[51] Zs. Páles. On homogeneous quasideviation means. Aequationes Math., 36(2-3):132–152, 1988.
[52] Zs. Páles. Extension theorem for functional equations with bisymmetric operations. Aequationes Math., 63(3):266–291, 2002.
[53] Zs. Páles and L. Székelyhidi. Laudation to Zoltán Daróczy. Ann. Univ. Sci. Budapest. Sect. Comput., 40:9–20, 2013.
[54] Zs. Páles and A. Zakaria. On the invariance equation for two-variable weighted nonsymmetric Bajraktarević means. Aequationes Math., 93(1):37–57, 2019.
[55] J. Rimán. On an extension of Pexider's equation. Zbornik Rad. Mat. Inst. Beograd (N.S.), 1(9):65–72, 1976. Symposium en Quasigroupes et Équations Fonctionnelles (Belgrade-Novi Sad, 1974).
[56] O. Sutô. Studies on some functional equations I. Tôhoku Math. J., 6:1–15, 1914.
[57] O. Sutô. Studies on some functional equations II. Tôhoku Math. J., 6:82–101, 1914.
[58] L. Székelyhidi. An extension theorem for a functional equation. Publ. Math. Debrecen, 28(3-4):275–279, 1981.