Beszélgetés Pach Jánossal
Mennyi idővel korábban kérnek fel egy plenáris előadót a kongresszusok előtt?
A 2014-es Szöulban rendezett világkongresszus előtt kb. másfél évvel kaptam meg a meghívást, fél évvel a kongresszus előtt pedig le kellett adnom az előadás szövegét, ami megjelent a hivatalos kötetben. Az európai kongresszus elvileg 2020-ban lett volna, engem egy évvel korábban kértek fel plenáris előadónak. Teljesen váratlanul ért a dolog, hiszen korábban csak két hazai matematikust, Babai Lászlót és Lovász Lászlót ért hasonló megtiszteltetés.
Hogyan választottad ki előadásod témáját?
Mivel az előadást eredetileg 2020-ban írtam, témája szorosan kapcsolódik az akkor induló From Geometry to Combinatorics and Back: Escaping the Curse of Dimensionality című ERC grantom kutatási programjához. Röviden arról van szó, hogy több fontos − teljes általánosságban reménytelenül nehéznek látszó − kombinatorikai feladatot először úgy próbálunk megoldani, hogy valamilyen értelemben korlátozzuk a vizsgált objektumok dimenzióját. Hogy éppen milyen dimenzió-fogalmat használunk, az a várható alkalmazásoktól vagy módszereink erejétől függ. Plenáris előadásról lévén szó, igyekeztem nemcsak precízen kimondani a szükséges definíciókat, de azt is érzékeltetni, hogy mi indokolja ezek bevezetését. Próbáltam úgy megfogalmazni a mondandómat, hogy az a témában teljesen járatlan matematikusok számára is követhető és − horribile dictu − érdekes is legyen.
A „kombinatorikus robbanás” fogalmát a következő anekdotával szokás illusztrálni:
Egy indiai király busásan meg kívánta jutalmazni a sakkjáték feltalálóját. Megígérte, hogy bármit megad neki, amit csak kér.
– Szerény leszek – mondta a feltaláló. – A tábla első kockájára egy szem búzát kérek, a másodikra kettőt, és minden továbbira kétszer annyit, mint az előzőre.
A király erre csak mosolygott, de hamarosan arcára fagyott a mosoly. Udvari matematikusa ugyanis elmagyarázta neki, hogy a földkerekség összes búzája is kevés lenne ahhoz, hogy ígéretének eleget tegyen.
Kombinatorikus robbanásnak hívjuk, ha egy feladatban szereplő mennyiségek a feladat (a fenti esetben a sakktábla) méretének függvényében legalább exponenciálisan nőnek. Ez a jelenség jellemez számos kombinatorikai optimalizációs feladatot. Ha a matematikusnak nincs jobb ötlete, akkor a feladat megoldásához lényegében az összes esetet végig kell néznie, ami sokszor reménytelen vállalkozás. A számítástudomány egyik fontos ága, a bonyolultságelmélet azzal foglalkozik, hogy mely problémák kezelhetőek hatékony algoritmusokkal és melyek nem. Milyen feladatokra van lényegesen gyorsabb megoldás, mint az összes eset megvizsgálása, és mik azok, amelyekre nincs, mert „eredendően” nehezek. Ez utóbbiaknál a matematikus kompromisszumokra kényszerül. Gyakran kénytelen megelégedni közelítő megoldásokkal. Néha ez sem segít, mert bizonyítható, hogy ugyanolyan nehéz közelítő megoldást találni, mint pontosat. A bonyolultságelmélet legmélyebb és legnehezebb tételei az alsó korlátok, vagyis annak a bizonyítása, hogy egy feladat eredendően nehéz.
A kombinatorika és a gráfelmélet fiatal tudományok. Bővelkednek megoldatlan problémákban, híres sejtésekben, melyek eldöntése fontos lenne a továbbhaladás szempontjából. A kombinatorikus robbanás jelensége következtében gyakran esélyünk sincs arra, hogy egyes sejtések helyességét ellenőrizzük legalább kis, mondjuk 10–20 pontú gráfokra. Más „praktikákhoz” kell folyamodnunk. Előadásomban olyan kérdéseket vizsgáltam, melyek kezelhetővé válnak, ha megszorítjuk őket – valamilyen értelemben – korlátos dimenziójú gráfokra vagy hipergráfokra. Az egyik lehetséges megszorítás, hogy feltesszük, hogy a szóban forgó struktúrák beágyazhatók egy alacsony dimenziós euklideszi térbe. Ez esetben gyakran támaszkodhatunk geometriai intuíciónkra, hiszen az euklideszi terekről rengeteg ismerettel rendelkezünk. Például felvághatjuk a teret – és benne az adott struktúrát – kisebb darabokra. Ha feltesszük, hogy ezekre a darabokra már igazoltunk egy sejtést, akkor megpróbálhatjuk a bizonyítást kiterjeszteni az általános esetre. „Csak” annyit kell belátnunk, hogy a parciális megoldások ügyesen összekombinálhatóak. Egy másik lehetséges megszorítás, hogy feltesszük, hogy az általunk vizsgált gráfok, hipergráfok Vapnyik–Cservonyenkisz-dimenziója korlátos, vagy eleget tesznek valamilyen hasonló algebrai feltételnek, amely garantálja, hogy kombinatorikus szerkezetük egyszerű. Ezek a dimenziófogalmak korábban már hasznosnak bizonyultak a matematikai statisztikában és a tanuláselméletben, de kombinatorikában és geometriában való alkalmazásuk viszonylag újkeletű.
Hogyan zajlik egy online kongresszus?
Tulajdonképpen hasonlóan a szokásos jelenléti konferenciákhoz. Többnyire egy neves matematikus elnököl, aki röviden bemutatja a meghívottat. Utána következik az előadás. Az Európai Kongresszusnak hivatalosan 1700-1800 résztvevője volt, közülük több százan regisztráltak az előadásomra. Remélem, hogy néhányuk érdekődését sikerült felkeltenem a téma iránt. A kongresszust követő hetekben sok kérdést és visszajelzést kaptam email-en, de egy „chat” vonalon az előadás alatt is érkeztek kérdések, megjegyzések. Minden esetben az elnök dönti el, hogy ezek közül melyeket olvassa fel.
A webinárium hátránya, hogy az előadó nem csak a hallgatóságot nem látja, de még saját magát sem. Fogalma sincs például arról, hogy kilóg-e a képből. Közvetlen kapcsolat híján nem érzékeli, ha bizonyos dolgok megértése nehézséget okoz a hallgatóságnak, és menet közben nem változtathat az előadásán. Közönséges zoom esetén legalább néhány arcot látunk a képernyőn, és nincs az az érzésünk, hogy a falnak beszélünk.
A kongresszus során milyen előadásokat hallgattál meg?
A programfüzetből előre kiválasztottam, hogy mely előadások érdekelnek, és csak azokat hallgattam meg. Egy kongresszusi központban valahogy el kell tölteni a kijelölt előadások közötti időt. Ha Portorožban lettem volna, nyilván beülök olyan előadásokra is, amelyek témája kevésbé izgat. Ilyenkor sokat tanulhat az ember, rácsodálkozhat arra, hogy milyen nagy és szerteágazó tudomány a matematika. Ha szerencséje van, akkor a tanultakat később a saját kutatási területén is kamatoztatni tudja.
A plenáris előadások nagy részét meghallgattam. Egy volt közöttük, amelynek témája kapcsolódik a kutatásaimhoz, és fontos szerepet játszik a konvexitás elméletében (Monika Ludwig: Geometric Valuation Theory). Egy másik plenáris előadó, Alfio Quarteori alkalmazott matematikus, a szív véráramlásának modellezéséről beszélt. A szív bonyolult szerkezet. Működéséről rengeteg adat áll rendelkezésünkre. Mérni tudjuk a vérnyomást, a szív összehúzódásának ritmusát, CT segítségével képet alkothatunk a sejtszövet állapotáról stb. Ha mindezek alapján sikerül jó modellt alkotnunk, akkor ezáltal jóval olcsóbban és egyszerűbben diagnosztizálhatjuk a szívrendellenességeket. A munka interdiszciplináris csapatot igényel. A felhasznált matematikai módszerek sokfélesége komoly kihívás elé állította a hallgatóságot – beleértve engem is.
A 10 plenáris előadón kívül még 30-an voltak meghívottak.
Egyikük, Daniela Kühn kombinatorikus. Persze az ő előadását is meghallgattam. Erdős, Faber és Lovász egy fél évszázados sejtéséről beszélt, amelyet idén oldott meg Kanggal, Kelly-vel, Methukuval és Osthus-szel közösen. Az indiai származású Abhishek Methuku egyébként Győri Ervin vezetésével Budapesten szerezte a PhD-jét, a Central European University-n, utána a tanszékemen volt postdoc, Lausanne-ban.
Egy magyar meghívott előadó volt, ifj. Székelyhídi László személyében, aki a Max Planck Intézetben szerzett doktori fokozatot, és a Lipcsei Egyetem professzora. Persze őt is meghallgattam. Édesapja, id. Székelyhídi László és fivére, Székelyhídi Gábor, aki az University of Notre Dame-on tanít, szintén kiváló matematikus. 2014-ben a szöuli világkongresszuson mindhármukkal találkoztam.
Az idei program külön érdekessége volt, hogy a szervezők felkérték Lovász Lászlót egy Abel-előadás megtartására.
Ha jól tudom, voltak a kongresszuson népszerűsítő előadások is.
A szélesebb nagyközönségnek szánt előadásokat eredetileg egy több ezer ember befogadására alkalmas konferenciateremben tartották volna, de sajnos nagyközönség hiányában ezek is online zajlottak. Az előadók között 3 még ma is viszonylag fiatal Fields-érmes volt: Andrei Okounkov (algebrai geométer), Stanislav Smirnov (matematikai fizikus) és Martin Hairer (sztochasztikus analista). Mindhárman ragyogó előadást tartottak. Bojan Mohar gráfok kereszteződési számairól beszélt, ami az én témámhoz is kapcsolódott.
Az egyik kísérő rendezvény egy matematikai témájú bélyegkiállítás volt, melyet Robin Wilson szervezett. Magam is bélyeggyűjtő vagyok, nagyon sajnálom, hogy erről lemaradtam. Wilson régebben gráfelmélettel foglalkozott, aztán átnyergelt matematikatörténetre. Édesapja, Harold Wilson 1974-76 között az Egyesült Királyság miniszterelnöke volt.
A kongresszussal kapcsolatban még egy dolgot feltétlenül meg szeretnék említeni. Az előadók körülbelül egyharmada nő volt. Korábban soha nem tapasztaltam ilyen arányt egyetlen matematikai konferencián sem. Biztos vagyok benne, hogy a programbizottság erre különös hangsúlyt fektetett. Önmagában is sokat számít, ha egy konferencia legrangosabb előadásaira nőket kérnek fel. A hallgatóság körében sok az egyetemi hallgató. Ha ilyen példát látnak, az vonzerőt jelenthet további életpályájukra nézve. Visszatekintve az elmúlt fél évszázad hazai tudományos életére, a nemek közti egyenlőségre vonatkozó hangzatos szavak és a valóság köszönő viszonyban sem volt egymással. Nagyon kevés női kutató jutott például az akadémikusi rangig. Nem csoda, hogy közülük többen felemás módon viszonyulnak annak említéséhez is, hogy ők nők; szívesebben tekintik magukat az adott tudományterület jeles képviselőjének, aki történetesen nő.
Ez az intézetünkben dolgozó fiatal női kutatóknál is megfigyelhető. Nem igényelnek semmilyen megkülönböztetést. Másrészt az utánpótlás-nevelés szempontjából hasznos őket bemutatni, példaként állítani a Lányok napján és hasonló pályaorientációs rendezvényeken.
Teljes mértékben egyetértek.
Kikből áll a kutatócsoportod?
A GeoScape csoportban jelenleg öten vagyunk: rajtam kívül Barát János, Tardos Gábor, Tóth Géza Budapesten, Frankl Péter pedig Japánban. Ő elsősorban halmazrendszerekkel foglalkozik, de ez is erősen kötődik a témánkhoz. Mindnyájan világhírű matematikusok, több tucat közös cikket írtunk egymással. Nagyon jól tudunk együtt dolgozni. Remélem, hamarosan sikerül csoportunk létszámát bővíteni. A munka első évében a pandémia miatt minden bizonytalan volt. Nem lett volna sok értelme egy posztdoktort Budapestre csábítani. A majdani postdoc-ok kiválasztásánál fontos szempont, hogy lehetőleg olyan kollégát találjunk, akinek érdeklődése kicsit eltér a mienkétől, és az is előny, ha jól tud programozni.
Az ELTE TTK-n végeztem, a programozással is ott találkoztam először. Évente mindössze egy-két lyukkártyás programot kellett írnunk, de ezek futtatása igen körülményes és lassú volt, különösen, ha hibáztunk. A tankörünkben volt egy diák, aki félállásban számítógépen dolgozott. Legtöbbünk helyett ő írta meg a programokat. Hibátlanul, néhány perc alatt. Manapság a matematikusképzésben nagyobb súllyal szerepel a programozás. Óriási hátrányban van valaki, ha még egy rövid programot sem tud megírni. Különösen igaz ez a kombinatorikában, ahol sok sejtést nem csak érdemes kis mintákon kipróbálni, de lehetséges is. A legkisebb esetek ellenőrzéséhez gyakran nem is kell nagyon „okos” programot írni.
Tudnál olyan megoldatlan feladatot mondani, ahol a számítógépes megközelítés hasznos lehet?
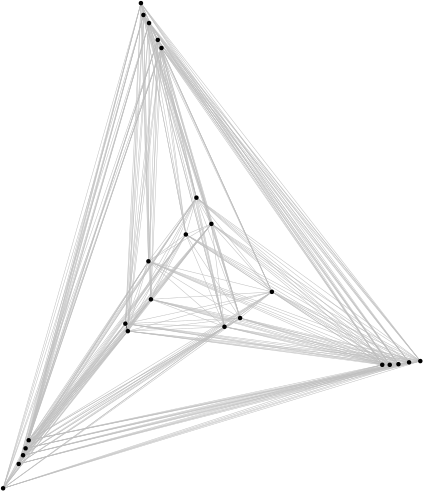
Különösen érdekelnek bennünket az olyan kérdések, hogy hány különböző módon lehet ugyanazt a gráfot lerajzolni a síkban. Milyen kombinatorikus- és metszettulajdonságokkal rendelkezik egy ilyen lerajzolás? Vegyünk N tetszőleges pontot a síkban, és bármely kettőt kössünk össze egy egyenes szakasszal. A szakaszok száma N(N−1)/2. Ez lényegesen több, mint a 3N−6, tehát Euler egy tétele szerint biztosan lesz közöttük kereszteződés. Azt sem nehéz belátni, hogy ha a szakaszok számának nagyságrendje N2, akkor a kereszteződések számának nagyságrendje N4. Azt viszont nem tudjuk, hogy ki lehet-e mindig választani konstansszor N szakaszt úgy, hogy azok páronként messék egymást. Azt sejtjük, hogy igen. Ennek a problémának a megoldásában talán segíthet a számítógép. Úgy is próbálkozhatunk, hogy véletlenszerűen veszünk fel pontokat egy körben, és megnézzük, hogy erre a ponthalmazra mi a válasz. Ha a pontok egy kör határán vannak és N páros, akkor mindig van N/2 páronként metsző szakasz. Egyébként gráfok és hipergráfok 3-dimenziós reprezentációja is számos érdekes matematikai kérdést vet fel. Az ilyen tipusú feladatoknál sokszor segít, ha bizonyos példákat le is rajzolunk. Mi nem írunk rajzoló programokat. Olyan kérdésekkel viszont gyakran foglalkozunk, amelyek megoldása felhasználható ilyen algoritmusok tervezésében.
Milyen valós problémákhoz kapcsolódnak a kutatásaitok?
Erre jó példa a kereszteződési szám fogalma, amely Turán Pál úgynevezett Téglagyári problémája kapcsán vált ismertté.
Turán Pál 1944 júliusában munkaszolgálatosként egy Pest környéki téglagyárban dolgozott. Társaival téglákkal teli vagonokat kellett ide-oda tolnia a kemencék és a raktárak között. A kereszteződéseknél a vagonok nagyot zökkentek és megakadtak. Megfogalmazódott benne a kérdés, hogy újra lehetne-e tervezni a sínrendszert kevesebb kereszteződéssel.
Egy G gráf kereszteződési száma az a legkisebb szám, ahány kereszteződéssel G lerajzolható a síkban.

A téglagyári problémát a háború után Erdős Pál, a matematika utazó nagykövete terjesztette. Többen próbálkoztak a feladat megoldásával abban a speciális esetben, amikor G teljes páros gráf, sőt, néhány ezzel kapcsolatos cikk is megjelent, de ezek mind hibásnak bizonyultak. A válasz ma sem ismert. A kérdést Turántól függetlenül egy angol konstruktivista festő, Anthony Hill is felvetette. Őt főképp az az eset foglalkoztatta, amikor G teljes gráf. A téma iránti érdeklődés a múlt század 70-es, 80-as éveiben ugrott meg, amikor Tom Leighton kutatásai nyomán kiderült, hogy egy elektromos hálózatot realizáló legkisebb nyomtatott áramkör vagy mikrochip mérete épp a hálózat gráfjának kereszteződési számától függ. Azóta több ezer cikk és számos monográfia jelent meg ezzel kapcsolatos kombinatorikai, algoritmikus és topológiai kérdésekről.
A felmerülő feladatok egy részének megoldásához csak egy jó ötlet kell, semmilyen matematikai előismeretre nincs szükség. Egy középiskolai matematikaszakkör számára fel lehetne építeni belőlük egy 5−6 foglalkozásból álló modult.
Talán a Rényi Intézet új Szakmódszertani osztálya vevő lesz erre a témára.
Nem tudom, mennyire vadásznak ötletekre; ötletben talán nincs hiány. A kérdés az, hogy van-e emberük, aki kézbe venné az ügyet. Lehet, hogy nyitottak rá, majd megkérdezem őket.
A veled készült Qubit interjúban a magyar matematikaoktatás helyzetéről is beszéltél. A következő 5 évben 22.000 tanár megy nyugdíjba, és nincs elég utánpótlás.
Sokan csak szerelemből tanítanak, de nem szerencsés erre építeni egy oktatási rendszert. A matematikát illetően mégis kicsit optimistább vagyok. A matematikát tanulók között talán több a megszállott, aki feltétlenül tanítani szeretne. De ha megszállottnak kell lenned ahhoz, hogy matematikát tanulj, s majd taníts, akkor nem feltétlenül a legjobb diákok jelentkeznek tanárszakra, és nem javul az oktatás minősége. Azért is bizakodom, mert a dolgok sokszor másképp alakulnak, mint gondolnánk. Az 1920-as években például kevesen számítottak arra, hogy hamarosan az Egyesült Államok lesz a világ vezető tudományos nagyhatalma. Aki 100 évvel ezelőtt Európából egy amerikai egyetemre ment kutatni és tanítani, az vagy kalandvágyból tette, vagy személyes okoknál fogva. Aztán jött Hitler, a náci hatalomátvétel, a háború, és tömegével vándoroltak ki Amerikába nem csak a jól képzett tudósok, de olyan diákok is, akik Európában remek alapképzést kaptak. A menekültek többsége szegény volt, de ambíciózus. Jó egyetemre akartak járni, de nem volt semmijük, ezért csak a legolcsóbb iskolákba tudtak jelentkezni. Ilyen volt a New York-i City College is, ahol korábban éveken át tanítottam. Egy abszolút közepes állami egyetem, melyet hirtelen elleptek a lelkes, tanulni vágyó európai fiatalok. A diákság színvonala akkorát nőtt, hogy az ott tanító professzoroknak fel kellett kötni a gatyaszárukat. Fel is kötötték. Mára a City College-nak annyi Nobel díjasa van, mint mondjuk a párizsi Ecole Normale Superieur-nek vagy a londoni Imperial College-nak. Nem azért, mert olyan ragyogó egyetem volt, hanem mert oda mentek a szegény diákok. Ez váratlan dolog volt, nem lehetett rá számítani. Ha egyszer valami beindul, és megvan a kritikus tömeg, akkor az láncreakciót válthat ki. Pláne, ha van hozzá pénz is! Az pedig volt, hiszen az 1950-es évek az amerikai gazdaság diadalmenetét hozták. Senki sem várta, senki sem tervezte, de megtörtént!
Nagyon remélem, hogy azokhoz a megrázkódtatásokhoz, amelyek együtt járnak az úgynevezett „egyetemi modellváltással”, jól fognak alkalmazkodni a hazai egyetemek. Ez egy váratlan, új helyzet, és nehéz megjósolni, hogy miként alakulnak a dolgok. Abban reménykedem, hogy nem lesz visszaesés. Elképzelhető, hogy kiemelkedik néhány kiváló egyetem, ahova ismét csak nagyon magas teljesítménnyel lehet bekerülni. Valamilyen csodában bízom én is.
Beszélgetőtárs: Szathmári Nóra.
Az eredeti interjú a Rényi Alfréd Matematikai Kutatóintézet honlapján jelent meg.









