A 2016-os Abel díjas Andrew Wiles számos jelentős eredménnyel gazdagította a matematikát, de a világhírt a nagy Fermat-tétel bizonyítása hozta meg számára: ha ![]() , akkor az
, akkor az ![]() egyenletnek nincsen olyan megoldása, ahol
egyenletnek nincsen olyan megoldása, ahol ![]() zérustól különböző egészek.
zérustól különböző egészek.
Fermat ezt az állítást Diofantosz Aritmetikájának olvasása közben jegyezte fel. Az állítás, hogy az ![]() egyenletnek nincs pozitív egész megoldása, könnyen érthető, de a bizonyítás évszázadokba telt.
egyenletnek nincs pozitív egész megoldása, könnyen érthető, de a bizonyítás évszázadokba telt.
 |
| Az Aritmetika Fermat jegyzeteivel ellátott kiadásából. A híres bejegyzés: “Cubum autem in duos cubos, aut quadrato-quadratum in duos quadrato-quadratos, et generaliter nullam in infinitum ultra quadratum potestatem in duos eiusdem nominis fas est dividere cuius rei demonstrationem mirabilem sane detexi. Hanc marginis exiguitas non caperet.” Avagy Bródy Ferenc míves fordításában: „Nincsen mód viszont felosztani köböt két köbre, sem négyzetes négyzetet két négyzetes négyzetre, és általában a négyzeten túl a végtelenig semmiféle hatványt két ugyanolyan nevezetűre; mely dolognak igazán csudálatos bizonyítását találtam. Szűkebb a margó, semhogy befogadná.” |
De ki volt Diofantosz? Miről szólt az Aritmetika, és mi motiválta Fermat-t a híres megjegyzésre?
Az első kérdésre nincs kielégítő válaszunk. Sem Diofantoszról, sem tanárairól, sem tanítványairól nincsenek adataink. Ami biztos, hogy az i.e. 2. század és az i.sz. 4 sz. között élt, valószínűleg az i. sz. 2-3. században.
|
Diofantoszról a következő rejtvény maradt fenn. Az olvasóra bízzuk, hogy megfejtse, hány évet élt a nagy matematikus, ha az alábbiakat tudjuk róla: Itt porlad Diofantosz mester, sírköve rajta. |
Diofantosz fő műve, az Aritmetika, témájában, eszközeiben és kifejezésmódjában is teljesen eltér az általunk ismert klasszikus görög matematikától. Az eredetileg 13 kötetből csupán 6 maradt fenn görögül, további példányok arab nyelven kerültek elő 1968-ban. Az arab könyvek feladatai más számozásúak, alkalmanként különböznek is. A görög nyelvű kötetek nagy valószínűséggel Hüpátia kommentárjai az eredetiről. (Heath: A history of Greek mathematics.)
 |
| Hüpátia Raffaello vatikáni freskóján. (Vagy nem.) Hüpátia (i.sz. 360 körül-415). Egy kortársa, Konstantinápolyi Szókratész egyháztörténeti leírása szerint „élt ebben az időben Alexandriában egy hölgy, Hüpátia, Theon filozófus lánya, aki oly sikereket ért el az irodalom és a tudományok terén, hogy jóval előtte járt minden kortárs filozófusnak. Platón és Plótinosz iskoláját kijárva, a filozófia alapelveit tanította diákjainak, akik közül sokan messze földről érkeztek.” Az egyik ilyen diákja, Kürénei Szünésziusz, későbbi püspök, így írt egy levelében neki: „Legnagyobb veszteségem, hogy nem lehetek az ön isteni szellemének közelében”. Hüpátia munkái is elvesztek, csak az Aritmetika átdolgozása maradt fenn. |
A közhiedelemmel ellentétben Diofantosz elfogadott racionális számokat is megoldásként, mint a II. könyv híres 8. feladatában is, ami Fermat-t a híres margójegyzetre sarkallta. Habár megoldásként csak pozitív számokat fogadott el, számolás közben minden fenntartás nélkül használt negatív számokat is, tehát az elsők között ismerte fel a racionális számtest technikai előnyeit.
| Amikor a XVI. században Európában újra felfedezték Diofantosz munkáit, az egyik első olvasója Bombelli olasz matematikus volt. Ő az Aritmetikában szereplő problémák jelentős részét beépítette Algebra című könyvébe, de a negatív számok használatából inspirációt merítve komplex számokat is használt harmadfokú egyenletek megoldására. Például az |
Diofantosz egy mai szemmel ugyan kezdetlegesnek tűnő algebrai jelölésrendszert használt, ám ez jelentős előrelépés volt a hagyományos körmondatokban leírt algebrai konstrukciókhoz képest. Pl. a változót ![]() -val, a négyzetét
-val, a négyzetét ![]() -vel jelölte. A negatív előjelre a
-vel jelölte. A negatív előjelre a ![]() megfordítottját, vagyis
megfordítottját, vagyis ![]() -t használta. Ugyanakkor ezzel a jelöléssel csak egy változó hatványait tudta jelölni, ezért ha további paraméterek jelentek meg, azokat mindig konkrét számnak választotta.
-t használta. Ugyanakkor ezzel a jelöléssel csak egy változó hatványait tudta jelölni, ezért ha további paraméterek jelentek meg, azokat mindig konkrét számnak választotta.
Így a XIX. században már sok olvasó számára tűnthetett úgy, hogy a könyv ad hoc trükkök gyűjteménye, és a többség egyetértett Hankel szavaival, aki szerint „100 probléma tanulmányozása után sem fogja tudni megoldani a 101-edik problémát”. Pedig ez távolról sincs így, a jelölésrendszeren és a racionális számtest használatán túlmutatóan is alapvető módszerek jelentek meg az Aritmetikában, amit alább két fontos példával is illusztrálunk.
Az első példa a fent említett II. könyv 8. feladata, ami Fermat-t híres sejtése megfogalmazására sarkalta. „Propositum quadratum dividere in duos quadratos...” azaz „Osszunk egy négyzetet két négyzet összegére”. Diofantosz megoldása (a fenti képen látható latin szövegben az ![]() szám négyzetét
szám négyzetét ![]() jelöli, mi ehelyett a mai
jelöli, mi ehelyett a mai ![]() jelölést alkalmazuk) a következő.
jelölést alkalmazuk) a következő.
Legyen a négyzet 16. Legyen az egyik oldal ![]() , tehát a másik
, tehát a másik ![]() . Ez utóbbinak négyzetnek kell lennie. Egy olyan négyzetet képezek, amelynek oldala az
. Ez utóbbinak négyzetnek kell lennie. Egy olyan négyzetet képezek, amelynek oldala az ![]() tetszőleges többszöröse a(z eredeti) négyzet oldalával csökkentve. Ez
tetszőleges többszöröse a(z eredeti) négyzet oldalával csökkentve. Ez ![]() 1. Így ez a négyzet
1. Így ez a négyzet ![]() . Ezt egyenlővé teszem
. Ezt egyenlővé teszem ![]() -tel. Mindkét oldalhoz hozzáadok
-tel. Mindkét oldalhoz hozzáadok ![]() -t és kivonok
-t és kivonok ![]() -t. Így
-t. Így ![]() adódik, amiből tehát
adódik, amiből tehát ![]() következik. Tehát az egyik szám
következik. Tehát az egyik szám ![]() , a másik pedig
, a másik pedig ![]() . A két szám összege 16 és mindkettő négyzet.
. A két szám összege 16 és mindkettő négyzet.
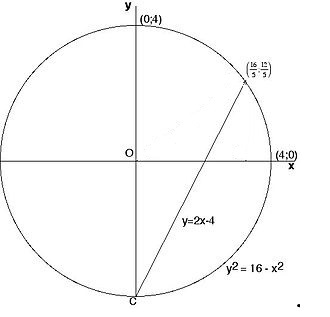
A megoldás a koordináta-geometria nyelvén jobban megérthető. Az ![]() körön keresünk olyan pontot amelynek mindkét koordinátája (pozitív) racionális szám. A nyilvánvaló
körön keresünk olyan pontot amelynek mindkét koordinátája (pozitív) racionális szám. A nyilvánvaló ![]() ponton át indítsunk egyenest, pl. Diofantoszt követve legyen ez az egyenes az
ponton át indítsunk egyenest, pl. Diofantoszt követve legyen ez az egyenes az ![]() egyenlettel megadva. Ez az egyenes két pontban metszi a kört, a
egyenlettel megadva. Ez az egyenes két pontban metszi a kört, a ![]() pontban, és a
pontban, és a ![]() pontban.
pontban.
| A módszer tetszőleges racionális meredekségű egyenesre ad egy új pontot. Ha |
A következő feladat megoldásának geometriai tartalma még érdekesebb.
IV. Könyv. 24. feladat. Bontsunk egy számot két részre, hogy a szorzatuk egy köb mínusz az oldal2. Diofantosz az „egy számot” 6-nak választja, így az
egyenletet kapja.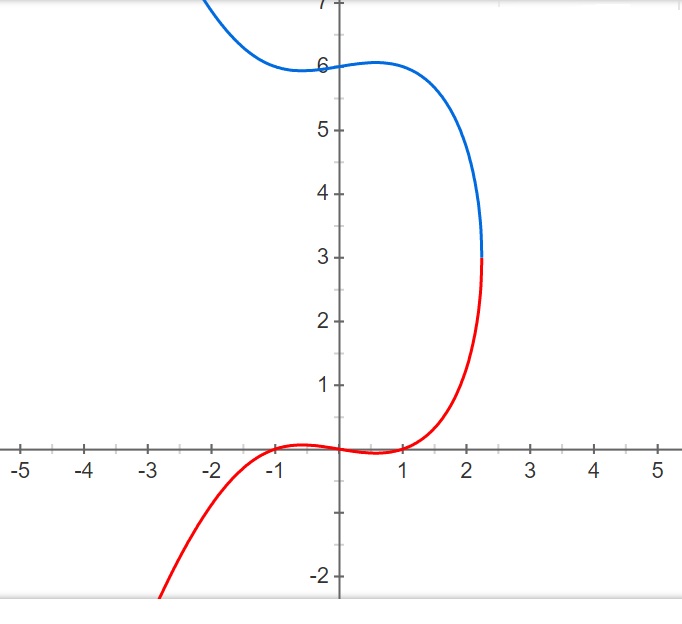
Ennek nyilvánvaló megoldása ![]() ,
, ![]() . Nem véletlen tehát, hogy Diofantosz megint így gondolkodik: Az
. Nem véletlen tehát, hogy Diofantosz megint így gondolkodik: Az ![]() szám legyen az
szám legyen az ![]() egy többszöröse eggyel csökkentve, azaz
egy többszöröse eggyel csökkentve, azaz ![]() . Ezután megkeresi
. Ezután megkeresi ![]() azon értékét amikor
azon értékét amikor ![]() -ben
-ben ![]() együtthatója
együtthatója ![]() . Ez akkor áll fenn, ha
. Ez akkor áll fenn, ha ![]() . Ekkor
. Ekkor ![]() , azaz
, azaz
![]()
Tehát ![]() és
és ![]() .
.
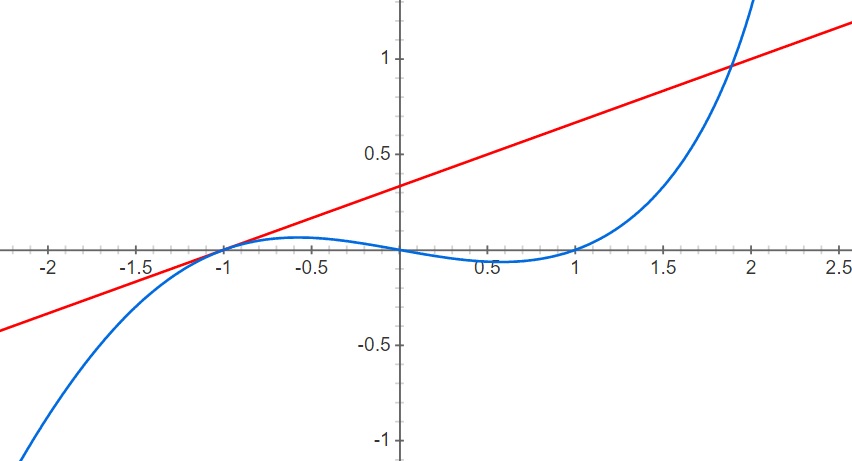
Talán az a legmeglepőbb az algebrai konstrukció ábráján, hogy Diofantosz itt egy görbe érintőjét konstruálja meg tisztán algebrai eszközökkel.
Az érintő-egyenes és a harmadfokú görbe metszéspontjai olyan racionális együtthatós harmadfokú polinomra vezetnek, aminek ![]() kétszeres gyöke, így a harmadik gyöknek is racionálisnak kell lennie. Ez ismét csak egy általános módszer, aminek mélységét csak a XX. században, az elliptikus görbék tanulmányozásával értettük meg. Ezek a görbék (lásd lejjebb) megkerülhetetlen szerepet játszottak Fermat sejtésének megoldásában.
kétszeres gyöke, így a harmadik gyöknek is racionálisnak kell lennie. Ez ismét csak egy általános módszer, aminek mélységét csak a XX. században, az elliptikus görbék tanulmányozásával értettük meg. Ezek a görbék (lásd lejjebb) megkerülhetetlen szerepet játszottak Fermat sejtésének megoldásában.
Érdekes módon Fermat (aki Descartes mellett a koordináta-geometria egyik megalkotója is volt), Diofantoszt olvasva vezette be a „közelítőleg egyenlő” fogalmát. Fermat a következő okoskodást használta maximumszámításhoz. Ha az ![]() függvénynek maximuma van
függvénynek maximuma van ![]() -ben, akkor
-ben, akkor ![]() közelítőleg egyenlő. Például, ha
közelítőleg egyenlő. Például, ha ![]() , akkor az
, akkor az ![]() közelítő egyenlőség akkor állhat fenn, ha
közelítő egyenlőség akkor állhat fenn, ha ![]() . Fermat „levezetése” komoly ellenállásba ütközött. A pontosítás kísérlete, a végtelenül kicsiny mennyiségek bevezetése, ugyan nem oldotta meg a logikai problémákat, de megfelelő nyelvet teremtett a dinamikusan változó mennyiségek leírására, és több mint 200 évig dominálta az analízist.
. Fermat „levezetése” komoly ellenállásba ütközött. A pontosítás kísérlete, a végtelenül kicsiny mennyiségek bevezetése, ugyan nem oldotta meg a logikai problémákat, de megfelelő nyelvet teremtett a dinamikusan változó mennyiségek leírására, és több mint 200 évig dominálta az analízist.
Visszatérve a harmadfokú egyenletekkel megadható görbékre, már Newton belátta, hogy ha egy ilyen egyenletknek van legalább egy racionális pontja (azaz egy olyan pont aminek mindkét koordinátája racionális szám, és „rajta van a görbén”, azaz kielégíti az egyenletet), akkor az a változók egyszerű helyettesítése után, megfelelő ![]() konstansokkal
konstansokkal
alakra hozható. Például a fenti IV. 28. feladat esetén, ![]() helyére
helyére ![]() -at,
-at, ![]() helyére
helyére ![]() -et írva az
-et írva az
egyenletet kapjuk.
Az ilyen típusú egyenletek által megadott görbét elliptikus görbének nevezzük, ha az ![]() harmadfokú polinom gyökei különbözőek, mert Weierstrass megmutatta, hogy ezek a görbék az Euler és Abel által tanulmányozott ú.n. elliptikus függvényekkel paraméterezhetők.
harmadfokú polinom gyökei különbözőek, mert Weierstrass megmutatta, hogy ezek a görbék az Euler és Abel által tanulmányozott ú.n. elliptikus függvényekkel paraméterezhetők.
A XX. század derekán Poincaré észrevette, hogy a Diofantosz által használt szelő-érintő konstrukció az elliptikus görbe pontjain csoport struktúrát eredményez. Ehhez ki kell egészíteni a görbét egy ![]() végetelen távoli ponttal; a függőleges egyenesek (és csak ezek) ugyanis csak két pontban metszenék a görbét, és a projektív geometria elvei alapján ezeknek a párhuzamos egyeneseknek a végtelen távoli közös metszéspontját adjuk a görbéhez.
végetelen távoli ponttal; a függőleges egyenesek (és csak ezek) ugyanis csak két pontban metszenék a görbét, és a projektív geometria elvei alapján ezeknek a párhuzamos egyeneseknek a végtelen távoli közös metszéspontját adjuk a görbéhez.
Ezzel a kiterjesztéssel a következő műveletet képezhetjük. Legyen ![]() és
és ![]() két pont a görbén. Vegyük a
két pont a görbén. Vegyük a ![]() és
és ![]() pontokon átmenő szelőt, vagy ha
pontokon átmenő szelőt, vagy ha ![]() , akkor a pontbeli érintőt. Ha az így kapott egyenes a
, akkor a pontbeli érintőt. Ha az így kapott egyenes a ![]() pontban metszi újra a görbét, legyen
pontban metszi újra a görbét, legyen
(Vegyük észre, hogy ez épp a ![]() pont tükörképe az
pont tükörképe az ![]() -tengelyre nézve.) Ha pedig a kapott egyenes függőleges, azt mondjuk majd, hogy
-tengelyre nézve.) Ha pedig a kapott egyenes függőleges, azt mondjuk majd, hogy ![]() . Az eredményül kapott
. Az eredményül kapott ![]() egy kommutatív, asszociatív művelet, amire nézve a görbe pontjai a végtelen távoli ponttal kiegészítve csoportot alkotnak. Az
egy kommutatív, asszociatív művelet, amire nézve a görbe pontjai a végtelen távoli ponttal kiegészítve csoportot alkotnak. Az ![]() példán illusztrálva a diofantoszi konstrukció a
példán illusztrálva a diofantoszi konstrukció a ![]() pontra a
pontra a ![]() pontot számítaná ki.
pontot számítaná ki.
Ennek a csoportnak a vizsgálata jelentős szerepet játszott a XX. század számelméletében. Ez a konstrukció, Diofantosz szellemében, bármely test (akár véges test) felett is megvalósítható. Egy talán váratlan meglepetésként, ezek a véges elliptikus görbék komoly szerepet játszanak modern kriptográfiai (vagyis titkosírás) alkalmazásokban.
Elliptikus görbék hozták meg a Fermat sejtés bizonyítását is. Frey (illetve korábban Helleougarch) javasolta, hogy a Fermat egyenlet egy hipotetikus ![]() megoldása esetén az
megoldása esetén az
elliptikus görbe nem lehetne moduláris. Ennek a gondolatnak a kifejtése külön cikket igényel, ami a következő számunkban jelenik majd meg.

A debreceni egyetem algebra és számelmélet tanszékének munkatársai
Végezetül pár szóban meg kell említenünk a diofantikus egyenletek hazai fellegvárát, a debreceni egyetem számelméleti kutatócsoportját. Ezt az iskolát Győry Kálmán teremtette meg, aki Alan Baker Fields-díjas matematikus módszerét fejleszette tovább. Megemlítendő, hogy Győry Kálmánon kívül, a csoport több más tagja, Pintér Ákos, Hajdu Lajos, Bérczes Attila is használták a Wiles-féle modularitási megközelítést, pl. az
egyenletcsaládra, ahol ![]() ,
, ![]() .
.
Tóth Árpád
ELTE, TTK Matematikai Intézet
Irodalomjegyzék
-
1. http://www.abelprize.no/nyheter/vis.html?tid=67106
2. Bashmakova, Isabella G., and Joseph H. Silverman. Diophantus and Diophantine equations. No. 20. Cambridge University Press, 1997.
-
3. Heath, Thomas Little, and Leonhard Euler. Diophantus of Alexandria: A study in the history of Greek algebra. CUP Archive, 1964.
4. Hellegouarch, Yves. Invitation to the mathematics of Fermat-Wiles. Academic Press, 2001. -
5. Koblitz, Neal. “Elliptic curve cryptosystems.” Mathematics of computation 48.177 (1987): 203-209.
-
6. Liptai, Kriptográfia. http://www.tankonyvtar.hu/hu/tartalom/tamop425/0038_matematika_Liptai_Kalman-Kriptografia/ch10s06.html#id538428
-
7. NSA. The case for Elliptic Curve Cryptography https://web.archive.org/web/20090117023500/http://www.nsa.gov/business/programs/elliptic_curve.shtml
-
8. Rónyai Lajos. Fermat utolsó tétele http://db.komal.hu/KomalHU/cikk.phtml?id=199401
-
9. Simon Singh: A nagy Fermat-sejtés (Park Könyvkiadó, Budapest, 1998
-
10. Stopple, Jeffrey. A primer of analytic number theory: from Pythagoras to Riemann. Cambridge University Press, 2003.
-
11. http://mta.hu/kozgyules2017/akademiai-elismereseket-adtak-at-az-mta-188-kozgyulesen-107676
-
Lábjegyzetek
1 Itt Diofantosz a jelölésrendszer hiányosságai miatt, tetszőleges többszörös helyett egy konkrét számot, 2-t, választ.
2 Ez mutatja, hogy Diofantosz nem hagyományosan gondolkodott, hiszen a megjelenő mennyiségeknek más dimenziójuk van, így egyenlőségük geometriailag értelmezhetlen.









