,,Mesterséges intelligencia” – ha úgy akarod
A Wolfram nyelv (archaikusan: Mathematica) többször is szerepelt már folyóiratunk hasábjain, de mivel nem elégszer, ezért most ismertetünk néhány aktuális érdekességet folytatva a programozásról szóló előző írásunkat. Amint bizonyára mindenki jól emlékszik, ott alapvető ismeretekről (a Map és az Apply függvényről) volt szó, itt viszont a másik végletről. Egészen összetett feladatok ellátására képes függvényekről.
Előkészületek
Azt a korábbi cikkben megtanultuk, hogy a Map operátort kell használnunk, ha ki akarjuk számolni az f függvény értékét az {a,b,c} lista elemein: Map[f, {a,b,c}] => {f[a],f[b],f[c]}. A függvényeket kifejezhetjük az identitásfüggvény segítségével is, aminek itt a jele #&. Ahelyett tehát, hogy f[x_]:=x^2+1, írhatjuk ezt is: f:=(#^2+1)&. Ezzel a jelöléssel a korábbi utasítás így írható: Map[(#^2+1)&, {a,b,c}]=> {a^2+1, b^2+1, c^2+1}.
Még egy előzetes megjegyzés: a cikk megírásához a sok rossz megoldás közül azt választottuk, hogy itt szövegesen, kevés Wolfram nyelvi szimbólumot használva ismertetünk néhány érdekesnek tűnő újdonságot, PDF-mellékletként pedig megmutatjuk a teljes Mathematica jegyzetfüzetet, aminek alapján a számolásokat reprodukálni tudja, aki rendelkezik licenccel.
Fordítás
Map[TextTranslation[”Where is the library?”,#]&,
{”Russian”,”German”,”Spanish”}
{”Где находится библиотека?”,”Wo ist die Bibliothek?“,“¿Dónde está la bibliotheque?“}
Nem gondolom, hogy az itt szereplő TextTranslation függvény a nagy áttörés, ráadásul jelenleg a Google vagy a Microsoft fordítói közül választhatunk módszert. Viszont ez alkalommal is megmutatkozik a program azon kellemetessége, hogy nem kell elhagyni egy fordítás kedvéért, hasonlóan ahhoz, ahogyan a számolásokon túl az ábrákat, a prezentációkat és a zenét is a programon belül lehet előállítani.
Ja, még egy hoppá: a Map operátor első argumentumában olyan kétváltozós függvény szerepel, amelynek első változóját rögzítettük a ”Where is the library?” értéken.
Bizonyítás
A kalkulus néhány elemi tételéből (szorzat és összeg deriválási szabálya) levezethető a parciális integrálás tétele. A kiindulásként feltett állításokat ezeket úgynevezett axiómaként adjuk meg. Azután megadjuk, hogy a bizonyítandó állítás a parciális deriválás tétele. Ebből a két argumentumból a FindEquationalProof függvény előállít egy bizonyítást, aminek a részleteit az alábbi táblázat formájában is megkaphatjuk.
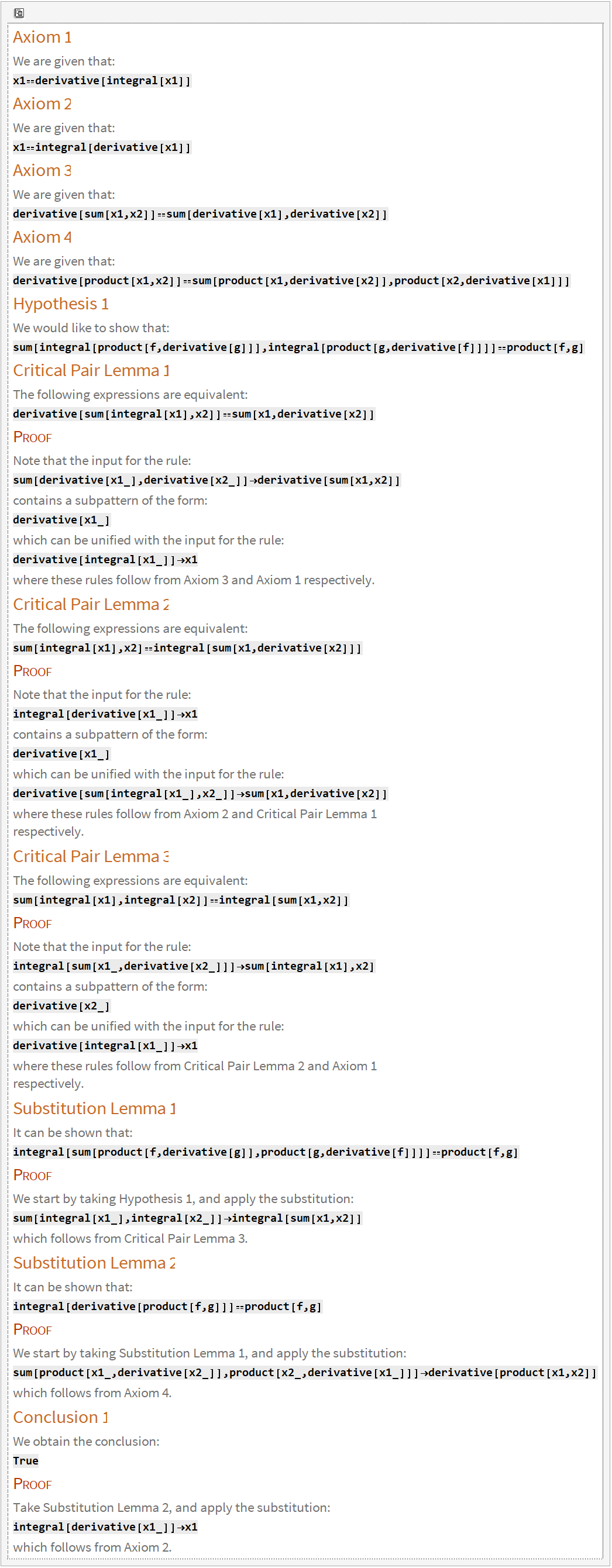
Itt annak lehet örülni, hogy – bár a tételbizonyításnak nem a Wolfram cég az élharcosa (erre speciális programokat szokás írni, univerzális programoknak tudomásom szerint nem részei) –, de most már ez is benne van a rendszerben. Az automatikus tételbizonyítás ma leginkább oktatási célra használatos, de vannak, akik új eredményeket képesek velük előállítani. A programoknak a jövőben ott lehet majd szerepük, ahol nem két-három kvantor áll egy tétel elején, hanem több tucatnyi.
Értő olvasás
A programnak, pontosabban a FindTextualAnswer függvénynek megadunk egy szöveget, és néhány olyan kérdést, amilyet a tanító néni szokott megfogalmazni. Az eredmény: a kérdésre adott helyes válaszok. (Legalább is a súgóban szereplő példa esetén 😊).
context="The population of Paris in its administrative city limits was 2,241,346 in January 2014. Paris is the capital and most populous city of France, with a 2015 population of 2,229,621. By the 17th century, Paris had become one of Europe's major centres of finance, commerce, fashion, science, and the arts, a position that it retains still today";
questions={"What is Paris?",
"When did Paris have a population of 2.24 million?",
"Why is Paris famous in Europe?"};
{{What is Paris?->{Paris is the capital and most populous city of France , with a 2015 population of 2,229,621.}},
{When did Paris have a population of 2.24 million?->{The population of Paris in its administrative city limits was 2,241,346 in January 2014 .}},
{Why is Paris famous in Europe?->{By the 17th century, Paris had become one of Europe's major centres of finance, commerce, fashion, science, and the arts, a position that it retains still today}}}
Ezt az újdonságot találtam a leglelkesítőbbnek, a Wolfram Alpha megalkotójához leginkább méltónak. Nyilvánvaló, hogy az itt alkalmazott FindTextualAnswer függvény ma még sok hibát követ el (ráadásul nem tud magyarul), de ebből még kijöhet valami (jó és rossz). Kicsit a – még kézzel végzett – tartalomelemzést juttatja az eszembe. (Antal László: A tartalomelemzés alapjai, Magvető Könyvkiadó, Budapest, 1976.)
Melléklet: Mathematica jegyzetfüzet letölthető PDF formában.
Tóth János









