A Bolyai Társulat díjai 2024-ben

Szele Tibor Emlékérem 2024

Az emlékéremre javasolhatók azok a matematika valamely ágában eredményes kutatók, akik egyúttal hozzájárulnak a magyar matematika tudományos utánpótlásának neveléséhez.

A 2024. évi Szele Tibor Emlékérem kitüntetettje Jordán Tibor, az ELTE TTK Matematikai Intézete Operációkutatási Tanszékének tanszékvezető egyetemi tanára, az MTA doktora. A díjat a díjbizottság elnöke, Laczkovich Miklós adta át:

Jordán Tibor 1991-ben szerzett diplomát az ELTE TTK matematikus szakán, majd 1995-ben kandidátus lett. Több évet töltött külföldön különböző egyetemeken (Bonn, Amsterdam, Odense, Grenoble, Aarhus). Meghívott kutatóként egy hónapot volt Párizsban, minikurzust tartott Lausanne-ban és Berlinben, 2012-ben és 2019-ben 3-3 hónapot töltött Kyotóban a RIMS intézetben.

Rényi Kató díjas, Grünwald Géza díjas, 2000-2003 között Széchenyi Professzori ösztöndíjas, 2004-ben elnyerte a Bolyai Kutatási ösztöndíjat, 2007-ben az Erdős Pál díjat.

Szerkesztője volt a Combinatorica és a SIAM Journal of Discrete Mathematics folyóiratnak. 2015–2019 között az ELTE TTK tudományos és nemzetközi ügyekért felelős dékánhelyettese, 2019-től a Matematika Doktori Iskola vezetője. 2010-ben vette át az Operációkutatási Tanszék vezetését Frank András professzortól. A Matematikai Intézetben a diszkrét matematika és a kombinatorikus optimalizálás szerepét tovább erősítette, új területeket (pl. merevségelmélet) bevonva a meglévő kutatási irányok mellé. Számos OTKA, illetve FKFP kutatási pályázatban vett részt, valamint volt vezető kutató. A 2017–2027 közötti időszakra az Egerváry Jenő Kombinatorikus Optimalizálási Kutatócsoport (EGRES) vezetőjeként nyert támogatást.

Számos tudományos konferencián tartott előadást, valamint több konferencia bírálóbizottságának volt tagja. Meghívott előadóként szerepelt neves konferenciákon és workshopokon (Oberwolfach, Banff).

Az MTMT és a Google adatbázisai szerint több mint 150 közlemény köthető a nevéhez, eredményeire többezer hivatkozással (MTMT: 1652, Google Scholar: 3153). Bill Jacksonnal közös, „Connected rigidity matroids and unique realizations of graphs” című cikke kimagasló számú, 493 (Google Scholar) hivatkozással rendelkezik.

Rendszeresen publikál a legrangosabb nemzetközi folyóiratokban, mint például Combinatorica, Journal of Combinatorial Theory B, SIAM Journal on Discrete Mathematics, SIAM Journal on Computing, Mathematical Programming, Journal of Graph Theory, Algorithmica, és magas presztízsű konferenciasorozatok kiadványaiba is bekerülnek munkái.

Jordán Tibor kiemelkedő szinten segíti és irányítja tehetséges fiatalok munkáját. 16 alap- vagy mesterszakos hallgató diplomamunkájának témavezetésében vett részt. Doktori témavezetettjei közül eddig négyen (Fekete Zsolt, Szabadka Zoltán, Kaszanitzky Viktória, Mihálykó András) szereztek fokozatot, egyikük (Garamvölgyi Dániel) abszolutóriumot, egy hallgató (Villányi Soma) pedig idén kezdte meg doktori tanulmányait az irányítása mellett.

Az elmúlt években az EGRES szeminárium szervezője. A szeminárium több mint 20 éve biztosít lehetőséget a kombinatorikus optimalizálás iránt érdeklődő fiatal hallgatók és kutatók számára arra, hogy egy heti rendszerességű találkozó keretében bemutathassák és megvitathassák a legújabb kutatási eredményeket. Emellett rendszeresen indít merevségelméleti szemináriumot, amelyen nagy hangsúlyt fektet könnyebb és nehezebb nyitott problémák kitűzésére, bevonva ezek révén hallgatóit a kutatómunkába.

Jordán Tibor meghatározó szerepet játszik a kétévente megrendezésre kerülő Japán-Magyar Diszkrét Matematika Konferencia szervezésében. A rendezvény mögötti több évtizedes együttműködés lehetővé teszi, hogy fiatal hallgatók és doktoranduszok látogassanak a másik országba.

Kiemelendők Jordán Tibornak a diákjaival az utóbbi években elért jelentős eredményei.
Garamvölgyivel, Királlyal és Villányival közösen sikerült pozitív választ adniuk Thomassen egy csaknem 40 éve nyitott sejtésére, miszerint minden kellően összefüggő gráfnak létezik k-összefüggő irányítása. A bizonyítás különlegessége, hogy egy tisztán összefüggőségi probléma megoldására merevségelméleti eszközöket használ. A kulcslemma annak megmutatása, hogy tetszőleges pozitív egész d és t számokra, minden 10 d (d + 1) t-összefüggő gráf tartalmaz t páronként éldiszjunkt d-merev feszítő részgráfot. Ez a látszólag technikai állítás egyben bizonyítást ad Kriesell azon 20 éve nyitott sejtésére, miszerint minden kellően összefüggő G gráfban létezik olyan T feszítőfa, amelyre G - T k-összefüggő.
Kiemeljük, hogy Jordán Tibor irányításával Villányi igazolta Lovász és Yemini egy több, mint 40 éves sejtését, és egyben annak egy Conelly, Jordán és Whiteley által megfogalmazott erősítését is. Az eredmény fontosságát jelzi, hogy Gil Kalai a blogján külön bejegyzést szentelt a tárgyalásának.

Összefoglalva, Jordán Tibor tudományos pályafutását számos elismerés kíséri, kiemelkedő szerepet játszik a hazai és nemzetközi matematikai közösségekben kutatóként és oktatóként is. Fontos, nehéz eredmények sorával bizonyította képességeit. A merevségelmélet nemzetközi szinten meghatározó kutatója. Hozzáállását, tudását igyekszik átadni diákjainak is, akik ennek köszönhetően már fiatalon is nemzetközileg elismert eredményeket értek el.

Grünwald Géza Emlékérem 2024

A Grünwald Géza Emlékérem jogelődjét, a Grünwald Géza Emlékdíjat a Bolyai János Matematikai Társulat 1951-ben alapította a matematikai alapkutatásban kiemelkedő tudományos eredményeket elérő, fiatal magyar matematikusok jutalmazására. 2018-ban a Társulat a jutalmazhatók körét kiterjesztette a Magyarországon tanulmányokat folytatott külföldi kutatókra is. 2024-ben a Grünwald Géza Emlékéremre hét felterjesztés érkezett. Közülük a Bizottság döntő többséggel kiemelkedő eredményeikre tekintettel hármójukat találta idén méltónak a kitüntetésre. Így a 2024-es díjazottak:

Földvári Viktória, a HUN-REN Rényi Alfréd Matematikai Kutatóintézet tudományos munkatársa és az ELTE TTK Geometria Tanszékének adjunktusa;
Sagmeister Ádám, az SZTE Bolyai Intézet adjunktusa;
Schwarcz Tamás, a HUN-REN-ELTE Egerváry Jenő Kombinatorikus Optimalizálási Kutatócsoport és az MTA-ELTE Lendület Matroidelmélet Kutatócsoport tagja.

Földvári Viktória 1992-ben született. Matematikus alap-, majd mesterszakos tanulmányait az Eötvös Loránd Tudományegyetemen végezte, majd 2016-tól ugyanitt doktori hallgató. Tudományos munkáját kisgyermeke születése miatt két évig szüneteltette. Disszertációját 2022-ben védte meg. Jelenleg a HUN-REN Rényi Alfréd Matematikai Kutatóintézet tudományos munkatársa, valamint az ELTE Geometriai Tanszékének adjunktusa.

Földvári Viktóriának 5 cikke jelent meg rangos nemzetközi folyóiratokban. Fő kutatási területe az alacsonydimenziós topológia, különösképpen a csomóelmélet. Emellett a diszkrét geometria területén is jelentős eredményeket ért el. Több munkájában foglalkozik kontakt sokaságokkal és Legendre-csomókkal. Becsléseket adott kéthidas csomók Legendre-realizációinak számára, valamint társszerzőivel egy új invariánst vezettek be, ami hiánypótlónak bizonyult a peremmel rendelkező kontakt 3-sokaságok ragasztása során. Az Üpszilon csomóinvariáns újradefiniálásával megnyitotta az utat csomók konkordancia-osztályainak kombinatorikus eszközökkel történő vizsgálatára. Diszkrét geometriai kutatásainak legfontosabb eredményei a társszerzőivel bizonyított kvantitatív Helly-típusú tételek, de a területen jelentős előrelépést ért el a μ-Minkowski elrendezésben elhelyezkedő testekre vonatkozó becslésével is.

Sagmeister Ádám 1994-ben született. Felsőfokú tanulmányait az ELTE-n végezte: 2018-ban BSc, 2020-ban MSc, majd 2024-ben PhD fokozatot szerzett. 2024 szeptemberétől a SZTE Bolyai Intézet Geometria Tanszékének adjunktusa.

Sagmeister Ádám 4 cikket publikált nemzetközi folyóiratokban, 4 további dolgozata bírálat és publikálás alatt van. Munkáiban különféle geometriai problémákat vizsgál állandó görbületű terekben. Ifj. Böröczky Károllyal új bizonyítást adtak az izodiametrikus egyenlőtlenségre, mely egyidejűleg működik mindhárom állandó görbületű téren tetszőleges dimenzióban, és belátták az izodiametrikus egyenlőtlenség egy közel optimális stabil változatát. Vizsgálták továbbá a Blaschke–Lebesgue-egyenlőtlenség állandó görbületű terekre vonatkozó kiterjesztéseit is. Társszerzőivel az irodalomban korábban bevezetett hiperbolikus szélességfüggvényeket vizsgáltak, valamint definiáltak egy új szélességfogalmat. Belátták, hogy valamennyi hiperbolikus szélességfüggvény folytonos, valamint, hogy ezek a G. Horváth-féle szélességfüggvény kivételével mind egybeesnek az állandó szélességű testek esetében. Sagmeister Ádám egyszerzős kézirataiban redukált sokszögeket vizsgált a hiperbolikus síkon. Belátta, hogy adott minimális szélesség mellett egy hagyományos redukált n-szög pontosan akkor maximális területű, ha szabályos. Továbbá megmutatta, hogy a hiperbolikus síkon adott minimális szélesség és csúcsszám mellett a hagyományos redukált sokszög kerülete épp a szabályos sokszögek esetén lesz minimális. Bizonyította azt is, hogy az adott minimális szélességű hagyományos redukált sokszögek átmérője és köréírt körének sugara egyaránt a szabályos háromszög esetében maximális, megválaszolva ezzel a terület extremitásán felül Lassak további három kérdését.

Schwarcz Tamás 1997-ben született. Felsőfokú tanulmányait az ELTE-n végezte: 2018-ban BSc majd 2020-ban MSc diplomát szerzett. Doktori tanulmányait is itt folytatja, jelenleg a MTA–ELTE Lendület Matroid Optimalizálás és Diszkrét Konvexitás Kutatócsoport tagjaként.

Schwarcz Tamásnak 7 cikke jelent meg rangos folyóiratokban, valamint 4 további dolgozata konferenciakiadványokban. Fő kutatási területe a matroidok elmélete. Schwarcz Tamás, témavezetőjével, Bérczi Kristóffal igazolt három híres, matroidok bázispárjainak cseretávolságaira vonatkozó sejtést split matroidok esetére. Ez a matroidosztály a tropikus geometria matroid politópjainak vizsgálata során kapott nagyobb figyelmet. Bizonyításuk algoritmikus, így eljárást is ad a kérdéses cseresorozat meghatározására. Mátravölgyi Bencével kiegészülve igazolták Gabow és White sejtéseit reguláris, vagy általánosabban, MFMC-matroidokra. Ezen eredményeknek messzemenő következményei vannak olyan területeken is, mint véletlen közös bázisok generálása, vagy éppen igazságos allokációk keresése.

Farkas Gyula Emlékdíj 2024

A Farkas Gyula Emlékdíj azoknak ítélhető oda, akik 35-ik életévüket még nem töltötték be, lehetőleg PhD fokozattal rendelkeznek, és a matematika alkalmazásaival szoros kapcsolatban álló jelentős tudományos tevékenységet folytatnak. A 2024-es díjazottak:

Dózsa Tamás, a HUN-REN SZTAKI tudományos munkatársa;
Regős Krisztina, a HUN-REN-BME Morfodinamika Kutatócsoport tagja;
Tekeli Tamás, a University of Trento posztdoktori kutatója;
Varga Kitti, a BME VIK Számítástudományi és Információelméleti Tanszék adjunktusa.

Dózsa Tamás Gábor programtervező informatikus BSc és MSc diplomáját egyaránt az Eötvös Loránd Tudományegyetem Informatikai Karán (ELTE IK) szerezte, 2017-ben, illetve 2020-ban. Ezt követően doktori tanulmányait is ugyanitt, az ELTE Informatikai Kar Doktori Iskolájában folytatta. A 2021 és 2024 közötti időszakban NVKDP Ösztöndíjban részesült, amelynek keretében az ELTE IK Numerikus Analízis Tanszék és a HUN-REN SZTAKI Rendszer- és Irányításelméleti Kutató Laborjában dolgozott. Tanszéki témavezetője Dr. Kovács Péter, míg vállalati szakértője és társ-témavezetője Dr. Soumelidis Alexandros volt. Az ösztöndíj ideje alatt tudományos segédmunkatársi beosztásban tevékenykedett, majd 2024 szeptemberétől a SZTAKI főállású munkatársa lett, emellett az ELTE IK Numerikus Analízis Tanszékének félállású oktatója is. PhD értekezését 2025 februárjában summa cum laude minősítéssel védte meg.

Oktatói pályafutása során aktívan részt vesz az ELTE IK Numerikus Analízis Tanszékének oktatási tevékenységében, valamint több hallgatója sikeresen szerepelt a kari és országos Tudományos Diákköri Konferenciákon, díjakat nyerve munkáikkal.

Kutatási területe a modellvezérelt gépi tanulási algoritmusok konstrukciója, amely a mesterséges intelligencia (MI) egy dinamikusan fejlődő ága. Ennek keretében a matematikai modellezés és az MI adatvezérelt szemléletének kombinálásával paraméterezett ortogonális transzformációkat – például projekciókat – épít be gépi tanulási algoritmusokba. Nemzetközi együttműködésekben is aktívan részt vesz, kiemelendő a linzi Johannes Kepler Egyetemi Kórházzal közös projekt, amelyben az EEG-jelek vizuálisan gerjesztett potenciáljainak reprezentációját és osztályozását vizsgálja. Ipari kapcsolatai révén a belgiumi Siemens Digital Industries Software kutatóival közösen publikált egy szenzormeghibásodás detektálásával foglalkozó tanulmányt is.

A SZTAKI Rendszer- és Irányításelméleti Kutató Laborjában olyan modellek fejlesztésén dolgozik, amelyek fizikai jelenségek elemzését és döntéshozatali folyamatok támogatását teszik lehetővé. Kutatásai során olyan paraméterbecslési módszereket dolgoz ki, amelyek leegyszerűsítik az irányítási rendszerek tervezését és megvalósítását. Különös figyelmet fordít az adatvezérelt módszerek alkalmazására, amelyek akkor válnak különösen fontossá, ha a hagyományos analitikus megközelítések a vizsgált rendszerek összetettsége miatt nem nyújtanak kielégítő megoldást. Kutatásai az autonóm járműirányítás területére is kiterjednek, különösen a járműfedélzeti rendszerekben alkalmazható hatékony detektálási és döntéshozatali algoritmusok fejlesztésére.

Új tudományos eredményei között szerepel a kerékszenzoros méréseken alapuló út-típus meghatározás. További kutatásai a talpponti kerékerők becslésére és a tapadási tényező meghatározására irányulnak, különös tekintettel a megcsúszás korai detektálására. Kutatásai során kidolgozott egy új racionális Gauss-wavelet transzformációt. Ennek alapján a mérésekhez igazított olyan idő-frekvencia felbontások állíthatók elő, amelyek együtt taníthatók mesterséges neurális hálózatokkal is. A módszer a járművekhez kapcsolódó detektálási problémák megoldása mellett számos egyéb területen, például vibroakusztika és hangfelismerés, is alkalmazható. A járműirányításhoz kapcsolódó kutatásokban a Széchenyi Egyetem Járműipari Kutató Központjával is együttműködik. Az autonóm járműveken végzett méréseire támaszkodó kutatások egyik alapját egy rendszer-póluskeresési módszer adja, amely lehetőséget biztosít lineáris dinamikus rendszerek nem-paraméteres identifikációjára.

Regős Krisztina 1998-ban született, majd 2016-ban érettségizett a szegedi Radnóti Miklós Gimnázium speciális matematika tagozatán. Tanulmányai során számos országos matematikaversenyen ért el kimagasló eredményeket. 2016-tól a Budapesti Műszaki és Gazdaságtudományi Egyetem Építészmérnöki Karán folytatta felsőfokú tanulmányait.

Egyetemi évei alatt jelent meg első három, társszerzős folyóiratcikke és első ismeretterjesztő cikke, szintén társszerzőkkel. Az egyik publikációja radikálisan új, algoritmikus megközelítést kínált egy John Horton Conway nevéhez fűződő, több mint hatvan éve felvetett, azóta is nagyrészt nyitott kérdéshez. A kutatás célja annak meghatározása volt, hogy egy monostatikus – vagyis egyetlen stabil vagy instabil egyensúllyal rendelkező – konvex poliédernek legalább hány lapja, csúcsa és éle lehet. Az első cikk eredményeire építve egy évvel később sikerült áttörést elérni, és először sikerült kiszámítani a minimális értéket egy speciális tömegeloszlás esetén.

2022-ben diplomamunkáját kitűnő eredménnyel védte meg, amelyben a térkitöltő mintázatokat, mint természeti jelenségek matematikai modelljeit vizsgálta. Ugyanebben az évben felvételt nyert a BME Csonka Pál Doktori Iskolájába, ahol Domokos Gábor vezetésével folytatja kutatásait. Diplomamunkájának témáját továbbfejlesztve, 2023-ban vezető szerzőként jegyzett egy cikket, amely egy új geometriai modellt mutatott be a szupramolekuláris mintázatok leírására. A publikáció a rangos Proceedings of the National Academy of Sciences of the United States of America folyóiratban jelent meg, társszerzői között pedig szerepel K. S. Novoselov Nobel-díjas fizikus is.

Szintén 2023-ban társszerzőként közreműködött egy, a térkitöltő mintázatok időbeli fejlődését vizsgáló tanulmányban, amely a matematikai fizika eszköztárára épült. Ezt követően egy újfajta térkitöltési osztállyal, az úgynevezett lágy mintázatokkal kezdett foglalkozni, amelyek minimális éles sarokkal rendelkeznek. Az erről szóló publikációja – amelyben meghatározó szerzőként szerepel – 2024 szeptemberében jelent meg, és kiemelkedő nemzetközi figyelmet kapott. A Nature magazin három napon át vezető hírként számolt be róla, emellett felfigyelt rá a Harvard Egyetem matematikai tanszéke és a torontói Fields Intézet is.

Tudományos munkája mellett kiemelt figyelmet fordít az ismeretterjesztésre. 2023-ban a BJMT által szervezett 62. Rátz László Vándorgyűlés egyik kiemelt előadója volt, azóta pedig rendszeresen tart népszerűsítő előadásokat gimnáziumokban és középiskolai matematika táborokban. 2022-ben előadott a Rényi Intézet Lányok Napja rendezvényén is. A HUN-REN-BME Morfodinamika Kutatócsoport tagja, valamint aktív szerepet vállal a csoport közös programjainak szervezésében. Meghívott előadóként szerepelt több neves egyetem, köztük a University of Bern, a University of Pennsylvania és a National University of Singapore szemináriumain.

Tudományos munkásságát számos ösztöndíjjal és elismeréssel jutalmazták. 2019-ben Strommer Gyula Ösztöndíjban, 2021-ben Ifjúsági Gábor Dénes Ösztöndíjban, részesült, diplomamunkáját a BME Építészmérnöki Kara Hauszmann-díjjal tüntette ki. Emellett 2022 óta folyamatosan elnyerte az NKFIH ÚNKP ösztöndíját, 2023-tól pedig a Doktori Kiválósági Ösztöndíj támogatását is élvezi. Tudományos kutatásait 2022 óta az Albrecht Science Fellowship segítségével végzi.

Tekeli Tamás 1993-ban született. A Szegedi Tudományegyetemen szerezte meg BSc és MSc diplomáját matematikából, majd 2023-ban ugyanitt védte meg doktori disszertációját. Tudományos munkásságát kezdettől fogva Röst Gergely irányította, témavezetője volt szakdolgozatának, diplomamunkájának, doktori értekezésének és OTDK-dolgozatának is, amellyel második díjat nyert az Országos Tudományos Diákköri Konferencián. Három alkalommal részesült az Új Nemzeti Kiválóság Program ösztöndíjában. Tudományos pályáját a dinamikai rendszerek területén kezdte, szakdolgozatában a Bendixson-kritérium egy következményét vizsgálta. Később érdeklődése a járványterjedés matematikai modellezése felé fordult, amely azóta is fő kutatási területe. Jelenleg az olaszországi Trentóban dolgozik posztdoktori kutatóként Andrea Pugliese professzor csoportjában, aki korábban az Európai Matematikai és Elméleti Biológiai Társulat elnöke volt.

Első tudományos publikációja Dénes Attila vezetésével született és a Scientific Reports folyóiratban jelent meg. Ebben társszerzőivel együtt egy olyan szezonális modellt dolgoztak ki a Zika-láz terjedésére, amely magyarázatot adott az egyes latin-amerikai országokban megfigyelt eltérő járványdinamikai mintázatokra. Röst Gergellyel közös első kutatása egy olyan SIS típusú járványmodellt vizsgált, amelyben a fertőzöttek egy lineáris láncon keresztül haladnak végig, modellezve a fertőzés stádiumait. Kimutatta, hogy ha a lánc legfeljebb három lépésből áll, az endemikus egyensúly mindig stabil, amikor létezik. Négy vagy több lépés esetén azonban stabil és instabil egyensúly is előfordulhat, és tetszőlegesen hosszú láncokra konkrét példákat is konstruált. Ezzel általánosította számos korábbi SIRS modell eredményeit, valamint kijavított egy korábban hibás következtetést az irodalomban.

2020-ban csatlakozott a Röst Gergely vezette COVID-19 Epidemiológiai és Modellezési Projekthez, amely a pandémia során a döntéshozók egyik legfontosabb tudományos tanácsadó testülete lett. Az ő számításai is hozzájárultak több jelentős döntés meghozatalához a járvány kritikus szakaszaiban. A témában két kiemelkedően idézett publikáció társszerzője: egyik a globális terjedési kockázatokat vizsgálta, és több mint 400 hivatkozással bír, míg a másik a magyarországi helyzetet elemezte, és 70 hivatkozást kapott.

Doktori értekezésének egyik központi témája a tesztelési stratégiák optimalizálása volt. Társszerzőivel kimutatta, hogy a csoportos tesztelés hatékonysága jelentősen javítható, ha a csoportméretet folyamatosan a járvány aktuális prevalenciájához igazítják. Legfrissebb kutatási eredményeit a dániai Pandemix csoporttal együttműködve publikálta, amelyek Dánia és Magyarország járványkezelési stratégiáját hasonlították össze, rávilágítva a tesztelési gyakoriság és a megfigyelhető járványgörbe közötti nem-triviális összefüggésekre.

Az alkalmazott matematika népszerűsítésében is aktív szerepet vállalt. A Zika-láz terjedéséről szóló tanulmányát a média széles körben ismertette, valamint a COVID-19 modellezés kapcsán is több ismeretterjesztő cikket publikált, például az Érintő folyóiratban. Emellett számos tudományos konferencia és rendezvény szervezésében vett részt, többek között a QTDE és CSM konferenciákon, az ECMI európai modellezési héten, a 2019-es BIOMAT konferencián, valamint a 2024-es Bolyai Társulat Alkalmazott Matematikai Konferenciáján.

Varga Kitti Katalin 1990-ben született Szombathelyen, ahol a Premontrei Rendi Szent Norbert Gimnáziumban érettségizett. Egyetemi tanulmányait a Budapesti Műszaki és Gazdaságtudományi Egyetemen (BME) végezte, ahol 2015-ben szerzett matematikus mesterfokozatot. Ezt követően ugyanitt folytatta doktori tanulmányait Katona Gyula Y. témavezetésével, PhD fokozatát 2021-ben védte meg.

Fiatal kutatói ösztöndíjasként dolgozott a Rényi Alfréd Matematikai Kutatóintézetben, emellett tagja a HUN-REN-ELTE Egerváry Kutatócsoportnak és az MTA-ELTE Momentum Matroid Optimization Kutatócsoportnak. 2024 szeptembere óta a BME Villamosmérnöki és Informatikai Karának Számítástudományi és Információelméleti Tanszékén főállású adjunktusként oktat. Több mint egy évtizede tanít kiemelkedő színvonalon, amelyet a Kar Kiváló Fiatal Oktatója díjjal ismert el – ráadásul kétszer is (2019, 2023), ami egyedülálló a díj történetében.

Kutatómunkájának egyik központi témája a minimálisan szívós gráfok vizsgálata. A t-szívós gráf egy olyan gráf, amelynek összefüggősége egy adott t paraméterrel mérhető, mely fogalom a gráfok megbízhatóságának és ellenállóképességének vizsgálatához kapcsolódik, és így fő alkalmazási területe a hálózatok megbízhatósága. Egy gráf minimálisan t-szívós, ha szívóssági értéke t, de bármely élének elhagyásával ez az érték csökken.

E témában négy, társszerzőkkel közösen írt folyóiratcikke jelent meg. Többek között igazolták, hogy minden n csúcsú minimálisan 1-szívós gráf minimális foka legfeljebb n/3 + 1. Emellett kimutatták, hogy a minimálisan t-szívós gráfok eldöntési problémája tetszőleges t esetén DP-teljes, valamint vizsgálták e gráfok létezésének kérdését különböző gráfosztályokban, például merev-körű, split, karommentes és 2K₂-mentes gráfokban.

Másik kiemelt kutatási területe az inverz optimalizálási problémák vizsgálata. Ezekben adott egy lehetséges megoldás, egy lineáris költségfüggvény és egy bemeneti megoldás, a cél pedig a költségfüggvény olyan módosítása, hogy a bemeneti megoldás optimálissá váljon – mindezt a lehető legkisebb változtatással. Társszerzőivel egy új inverz optimalizálási problémakört vezetett be, amelyben nemcsak egy, hanem k darab költségfüggvény adott, és ezeket egyetlen módosító vektorral kell úgy módosítani, hogy a bemeneti megoldás mindegyik függvény szerint optimális legyen. Három alapvető kombinatorikus optimalizálási problémára összpontosítottak: az inverz legrövidebb út, az inverz teljes párosítás páros gráfokban, valamint az inverz fenyőproblémák. Lineáris programozási módszerekkel min-max karakterizációkat adtak az optimális eltérítési vektor l₁-normájára, amelyeket a Discrete Applied Mathematics folyóirat közölt.

Eddigi eredményes publikációs tevékenységét 11 impakt faktoros folyóiratcikk és 5 konferenciakiadvány fémjelzi. Széleskörű kutatásai a kombinatorika és a számítástudomány különböző területeit ölelik fel, munkáinak jelentős része az alkalmazott matematikához kapcsolódik.

Rényi Kató Emlékdíj 2024

A Rényi Kató Emlékdíj olyan 25 évnél fiatalabbaknak adományozható, akik az előző év végéig még nem szereztek mesterfokú diplomát, de a matematika valamely ágában önálló tudományos eredményt értek el. 2024-ben a Bolyai János Matematikai Társulat három jelöltnek ítélte oda a Rényi Kató Emlékdíjat.

A díj I. fokozatában részesült:

Gárgyán Barnabás, az SZTE és a University of Warwick doktorandusza;

a díj II. fokozatában részesültek:

Borsik Anna Nóra, az ELTE Matematika Doktori Iskola hallgatója;
Kiss Csaba, a BME Sztochasztika Tanszékének doktorandusza.

Gárgyán Barnabás, a Szegedi Tudományegyetem, illetve a University of Warwick doktorandusza. Témavezetői Ambrus Gergely, illetve Keith Ball. Gárgyán Barnabás kutatásában analitikus és geometriai témákat ötvöz. Legerősebb eredménye magas dimenziós kockák centrális metszeteiről szól. Egy Ambrus Gergellyel közös cikkben egy klasszikus sejtést megcáfolva belátták olyan kritikus centrális metszetek létezését tetszőleges dimenzióban, amelyek normálvektora nem párhuzamos a kocka egyik lapátlójával sem. A cikk a nagyon rangos Advances in Mathematics folyóiratban jelent meg. Legújabb cikkükben a téma folytatásaként cáfolták azt a korábban bizonyítottnak hitt állítást, mely szerint a kocka alacsonyabb dimenziós átlós metszetei extremálisak.

Borsik Anna Nóra az Eötvös Loránd Tudományegyetem doktorandusza, témavezetője Madarasi Péter. Borsik Anna Nóra tágabb kutatási témája a diszkrét optimalizálás és a gráfelmélet, szűkebb területe gráfok egalitárius aciklikus rendezéséhez kapcsolódik. Egy Madarasi Péterrel közös cikkben irányított gráfok elbonthatóságának elméletét absztrahálták, ezáltal bizonyos rangsorolási és ütemezéselméleti problémákra polinomiális algoritmusokat kaptak, valamint belátták, hogy természetes általánosítások már NP-beliek. Egy újabb cikkben megmutatják, hogy az aciklikus egalitárius irányítasi feladat NP-nehéz, ami gyakorlati alkalmazások szempontjából is lényeges.

Kiss Csaba a Budapesti Műszaki és Gazdaságtudományi Egyetem doktorandusza, témavezetője Molontay Roland, korábban Vető Bálint. Kiss Csaba fő publikált eredménye a matematikai demográfia területéről származik Vető Bálinttal, valamint később Németh László demográfussal kiegészülve a világ legidősebb emberének életkorára vonatkozó modellt fejlesztettek és vizsgáltak meg részletesen. A cikk formájában leírt eredmény megjelent a neves Scientific Report folyóiratban. Emellett vannak további publikálatlan eredményei kölcsönható részecskerendszerek aszimptotikus viselkedéséről, valamint interpretálható gépi tanulásról, a nagy nyelv modellek és a kauzalitás kapcsolatáról is.

Patai-díj

A Bolyai János Matematikai Társukat Elnöksége által kijelölt bizottság a Patai-díjat 2024. november 18-i ülésén egyhangú szavazással az alábbi tanárok számára itélte oda: mindketten 40 évnél fiatalabbak és a matematikában vagy annak szakdidaktikájában jelentős tudományos eredményeket értek el.

Kardos Gergely (SZTE Gyakorló Gimnázium és Általános Iskola);
Lenger Dániel (ELTE Matematikai Intézet és Budapesti Fazekas Mihály Gyakorló Gimnázium).

Kardos Gergely 1998-ban született Hódmezővásárhelyen, tanulmányait Orosházán, majd a Szegedi Tudományegyetemen végezte matematika-fizika tanár szakon, ahol 2023-ban diplomázott. Egyetemi évei alatt kiemelkedő teljesítményével számos ösztöndíjat elnyert, többek között a Nemzeti Felsőoktatási Ösztöndíjat és az Új Nemzeti Kiválósági Program hallgatói kutatói ösztöndíját.

Kardos Gergely pedagógusi pályafutását az SZTE Gyakorló Gimnáziumban és Általános Iskolában kezdte meg. Tanítványai számos rangos matematikaversenyen értek el kiemelkedő eredményeket, köztük az Arany Dániel Matematikaverseny döntője és a Szőkefalvi Nagy Gyula Matematikaverseny dobogós helyezései is az ő felkészítő munkáját dicsérik.

Oktatói és nevelői munkája mellett doktori tanulmányait is példaértékűen végzi a Debreceni Egyetem Matematika és Számítástudományok Doktori Iskolájában, ahol kutatásai mellett konferenciák aktív résztvevője és szervezője. Tudományos eredményeit hazai és nemzetközi fórumokon is bemutatta, például a CME konferencián Lengyelországban, és a Szegeden rendezett MIDK-en.

Mindezek mellett a matematikai közösség aktív tagja: versenyek szervezője, lektora és feladatsorok készítője. Szabadidejében fizikát népszerűsítő rendezvényeken és diákok számára szervezett programokon vesz részt.

Kardos Gergely nem csupán kiváló szakember, hanem igazi közösségformáló személyiség, aki diákjai és kollégái körében is nagy tiszteletnek és szeretetnek örvend.

Lenger Dániel 2021-ben szerzett tanári diplomát az ELTE-n, azóta a Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium tanára. Pályafutása kiváló példája annak, hogy miként lehet egyszerre magas szintű kutatói és elhivatott tanári tevékenységet folytatni. Oktatói munkássága az ELTE TTK-n és a Fazekas Mihály Gyakorló Gimnáziumban kiemelkedő, ahol tehetséggondozó szakkörök vezetése, innovatív didaktikai módszerek alkalmazása, valamint tanítványainak hazai és nemzetközi versenyeken elért eredményei is bizonyítják pedagógiai sikerét.

Kutatóként elméleti matematika doktori tanulmányait summa cum laude minősítéssel zárta az ELTE Matematika Doktori Iskolájában, és számos nemzetközileg is elismert publikációja jelent meg olyan neves folyóiratokban, mint a Journal of Combinatorial Theory és a Discrete Applied Mathematics. Továbbá társszerzője a Typotex és a Springer kiadó gondozásában megjelent, a matematika népszerűsítését szolgáló köteteknek, amelyek nemcsak a tudományos ismeretek közvetítését, hanem a matematika iránti lelkesedés felkeltését is szolgálják.

Szervezőként és mentorként Lenger Dániel számos hazai és nemzetközi matematikai verseny előkészítésében és lebonyolításában vállalt kulcsszerepet, a tehetséggondozás iránti elhivatottságát pedig a diákolimpiai csapatok felkészítésében végzett munkája is tükrözi.

Jelentés a 2024. évi Kürschák József Matematikai Tanulóversenyről

A Bolyai János Matematikai Társulat a 2024. évi Kürschák József Matematikai Tanulóversenyt október 18-án, közép-európai idő szerint 14 órai kezdettel rendezte meg a következő tizenkét helyszínen: Békéscsaba, Budapest, Cambridge, Debrecen, Kaposvár, Kecskemét, Miskolc, Nyíregyháza, Pécs, Szeged, Székesfehérvár és Veszprém.

A Társulat elnöksége a verseny lebonyolítására az alábbi bizottságot kérte fel: Biró András, Fleiner Tamás (elnök), Frenkel Péter, Harangi Viktor, Kós Géza, Kovács Benedek (titkár), Maga Péter, Pach Péter Pál és Tóth Géza. A bizottság szeptember 13-i ülésén a következő feladatokat tűzte ki:

1. Az 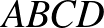$ABCD$ négyszöget olyan húrnégyszögekre bontottuk fel, amelyeknek páronként nincs közös belső pontjuk. A felbontásban szereplő húrnégyszögek csúcsai közül egy sem esik egy másik, felbontásbeli húrnégyszög oldalának vagy az 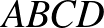$ABCD$ négyszög oldalának belsejébe. Bizonyítsuk be, hogy 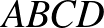$ABCD$ is húrnégyszög.

2. Az ókori Egydimenziós Birodalom egy egyenes mentén helyezkedett el. Kezdetben nem voltak városok. Egyenként alapítottak összesen 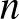$n$ különböző pontszerű várost; a másodiktól kezdve mindegyik újonnan alapított város és a hozzá legközelebbi, már létező város (ha két ilyen volt, akkor a régebbi) testvérvárossá nyilvánították egymást.

A birodalom fennmaradt térképén látszanak a városok és a köztük lévő távolságok, de alapításuk sorrendje nem. A történészek a térképből próbálnak arra következtetni, hogy mindegyik városnak legfeljebb 41 testvérvárosa volt.

(a) 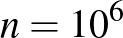$n=10^{6}$ esetén adjunk meg olyan térképet, amelyből ez a következtetés levonható.

(b) Igazoljuk, hogy 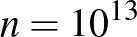$n=10^{13}$ esetén ez a következtetés semmilyen térképből sem vonható le.

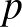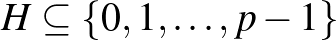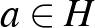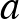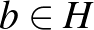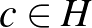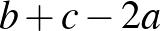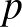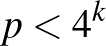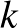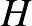3. Legyen $p$ prímszám és $H \subseteq \{0,1,\ldots,p-1\}$ nemüres halmaz. Tegyük fel, hogy minden $a\in H$ elemhez találhatók olyan, $a$ -tól különböző $b\in H$ és $c\in H$ elemek, amelyekre $b+c-2a$ osztható $p$ -vel. Mutassuk meg, hogy $p<4^{k}$ , ahol $k$ a $H$ halmaz elemeinek számát jelöli.

A feladatok és az előzetes megoldások letölthetők a Bolyai Társulat honlapjáról.

A bizottság a beérkezett dolgozatok átnézése után, december 6-i ülésén a következő jelentést fogadta el:

„A verseny minden helyszínen rendben zajlott le, 106 regisztrált versenyzőtől összesen 79 dolgozat érkezett be.

Az idei versenyen 28-an oldották meg az első feladatot kisebb-nagyobb hiányossággal. A második feladat esetén 39-en értek el érdemi eredményt a feladatnak legalább az egyik részében. A harmadik feladat azonban sajnos minden résztvevő számára megoldhatatlannak bizonyult, még csak értékelhető részeredmény sem érkezett egyetlen versenyzőtől sem. Ennek megfelelően a bizottságnak idén nem volt könnyű dolga a díjak odaítélésekor. A sok közel egyforma teljesítményt nyújtó versenyző közötti differenciáláskor a szokásosnál sokkal többet számított, hogy mennyire világos és teljes a megoldás leírása, és a megoldásokban előforduló kisebb hiányosságokat idén a szokottnál jóval szigorúbban vettük figyelembe. A bizottság számára idén is komoly nehézséget okozott néhány dolgozat elolvasása.

Mindezek alapján a versenybizottság idén I. díjat nem ad ki.

Öt versenyző helyesen oldotta meg az első és a második feladatot, ezért

II. díjat és 15 000 Ft pénzjutalmat nyer

Holló Martin, a Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium 11. osztályos tanulója (tanárai Hujter Bálint és Gyenes Zoltán),
Molnár István Ádám, a miskolci Földes Ferenc Gimnázium 12. osztályos tanulója (tanárai Dobos Sándor, Fejér Szabolcs, Győry Ákos, Grallert Krisztina, Kovács Benedek, Tóth Tibor és Vass Iván),
Simon László Bence, a Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium érettségizett tanulója, jelenleg a University of Cambridge hallgatója (tanárai Gyenes Zoltán, Kiss Géza, Hujter Bálint, Nagy Zoltán Lóránt, Surányi László és Borbényi Márton),
Szakács Ábel, a Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium 11. osztályos tanulója (tanárai Hujter Bálint, Gyenes Zoltán, Terpai Tamás és Dobos Sándor), végül
Varga Boldizsár, a Békásmegyeri Veres Péter Gimnázium 12. osztályos tanulója (tanárai Holló Gábor, Dobos Sándor, Gyenes Zoltán és Surányi László).

Hat versenyző apró hiányosságoktól eltekintve helyesen oldotta meg az első két feladatot. Ezért a teljesítményért

III. díjban és fejenként 15 000 Ft pénzjutalomban részesül

Bodor Mátyás, a csíkszeredai Márton Áron Főgimnázium 12. osztályos tanulója (tanára Páll Olga),
Hodossy Réka, a Balassagyarmati Balassi Bálint Gimnázium 12. osztályos tanulója (tanára Hegedűs Csaba),
Kocsis Péter, a Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium 11. osztályos tanulója (tanárai Hujter Bálint, Gyenes Zoltán és Kiss Géza),
Prohászka Bulcsú, a Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium 11. osztályos tanulója (tanárai Hujter Bálint, Gyenes Zoltán, Kiss Géza és Nagy Kartal),
Tarján Bernát, a Békásmegyeri Veres Péter Gimnázium érettségizett tanulója (tanárai Holló Gábor, Dobos Sándor, Nagy Zoltán Lóránt és Kovács Benedek), valamint
Vámosi Bendegúz Péter, a Debreceni Fazekas Mihály Gimnázium 11. osztályos tanulója (tanárai Remeténé Orvos Viola és Tóth Mariann).

Három versenyzőnek az első két feladatra adott megoldása kiegészítésre szorul. Ezért a teljesítményért

dicséretben részesítjük

Balla Ignácot, a Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium 9. osztályos tanulóját (tanárai Gyenes Zoltán, Farkas Gitta, Pósa Lajos),
Pázmándi József Áront, a Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium 9. osztályos tanulóját (tanárai Gyenes Zoltán, Farkas Gitta) és
Vigh Zalánt, a Szegedi Radnóti Miklós Kísérleti Gimnázium 11. osztályos tanulóját (tanárai Mike János, Schultz János).

A versenybizottság ezúton köszöni meg minden versenyző, felkészítő tanár és a lebonyolításban közreműködő kolléga munkáját, a díjazottaknak pedig további sikereket kívánva gratulál.”

A fenti jelentés, a feladatok és a részletes megoldások megjelentek a KöMaL 2025. februári számában (66-72. o.)

Jelentés a 2024. évi Schweitzer Miklós Matematikai Emlékversenyről

A Bolyai János Matematikai Társulat 2024. október 25. és 2024. november 4. között rendezte meg a Schweitzer Miklós Matematikai Emlékversenyt. A versenyen középiskolai tanulók, egyetemi és főiskolai hallgatók, továbbá azok vehettek részt, akik egyetemi vagy főiskolai tanulmányaikat 2024-ben fejezték be.

A verseny lebonyolítására a Társulat a következő bizottságot kérte fel: Keleti Tamás (elnök), Borbényi Márton (titkár), Ágoston Tamás, Elekes Márton, Frenkel Péter, Gáspár Attila, Harangi Viktor, Maga Balázs, Pach Péter Pál, Pálvölgyi Dömötör, Terpai Tamás, Weiner Mihály, Zábrádi Gergely, Zólomy Kristóf. A bizottság október 10-i ülésén kiválasztotta a 11 kitűzendő feladatot.

A bizottság köszönetét fejezi ki mindazoknak, akik feladatot javasoltak a versenyre. A kitűzött feladatokat javasolták: 1. Bérczi Kristóf, 2. Buczolich Zoltán, 3. Buczolich Zoltán, 4. Prokaj Vilmos, 5. Juhász István, 6. Maga Balázs, 7. Bodor Bertalan, 8. Damásdi Gábor, 9. Nagy Gábor, 10. Kós Géza, 11. Abért Miklós és Maga Balázs.

A verseny eredményes volt; 18 versenyző összesen 74 megoldást nyújtott be. A versenybizottság november 25-i ülésén a következő díjakat ítélte oda:

Egy versenyző oldott meg lényegében nyolc feladatot. Ennek alapján

1. díjban és 150.000 Ft pénzjutalomban részesül

Kocsis Anett, az ELTE másodéves matematikus mesterszakos hallgatója.

Kocsis Anett hibátlanul megoldotta az 1., 2., 3., 4., 6., 7., 8., illetve apró pontatlanságoktól eltekintve az 5. feladatot. Ezeken kívül értékelhető részeredményt ért el a 9. feladatban.

Három versenyző oldott meg kicsit több mint öt feladatot. Ennek alapján

2. díjban és 70.000 Ft pénzjutalomban részesül

Fleiner Zsigmond György, az ELTE harmadéves matematika alapszakos hallgatója,
Füredi Erik, az ELTE elsőéves matematika mesterszakos hallgatója és
Kökényesi Márk, az ELTE harmadéves matematika alapszakos hallgatója.

Fleiner Zsigmond György megoldotta az 1., 2., 5. és 8. feladatot, valamint kisebb hibáktól és hiányosságoktól eltekintve a 4. és a 6. feladatot.

Füredi Erik megoldotta az 1., 3., 4., 9. és 10. feladatot, valamint apróbb észrevételeket tett a 11. feladatban. A bizottság szeretné kiemelni, hogy a 9. és a 10. feladatra egyedül ő adott be teljes megoldást, ezeken kívül a 9. feladatban a becslés élességét is megmutatta.

Kökényesi Márk megoldotta az 1., 3., 5. és 7. feladatot, egy apró hibától eltekintve a 2. feladatot, valamint fontos részeredményeket ért el a 4. és 6. feladatban.

Négy versenyző oldott meg lényegében négy feladatot. Ennek alapján dicséretben és 30.000 Ft pénzjutalomban részesül

Duchon Márton Gergő, az ELTE elsőéves matematika alapszakos hallgatója,
Fraknói Ádám, az ELTE harmadéves matematika mesterszakos hallgatója,
Jánosik Máté, az ELTE harmadéves matematika alapszakos hallgatója és
Németh Márton Tamás, a Cambridge University másodéves matematika alapszakos hallgatója.

Duchon Márton Gergő megoldotta az 1., 2. és 5. feladatot, valamint apróbb hibáktól eltekintve a 4. feladatot, továbbá értékelhető részeredményt ért el a 11. feladatban. Fraknói Ádám megoldotta az 2., 4. és 5. feladatot, valamint egy könnyen javítható hibától eltekintve az 1. feladatot.

Jánosik Máté megoldotta az 1., 2. és 3. feladatot, valamint értékes részeredményeket ért el a 4. feladatban.

Németh Márton Tamás megoldotta 1., 4. és 8. feladatot, valamint apróbb hiányosságtól eltekintve az 5. feladatot, továbbá részeredményt ért el a 3. feladatban.

További három versenyző oldott meg teljesen két feladatot és ért el fontos részeredményeket legalább egy másik feladatban. Ennek alapján elismerő oklevelet kap

Bognár András Károly, az ELTE másodéves matematika alapszakos hallgatója,
Földesi András, az ELTE-n matematika alapszakott végzett, jelenleg a BME negyedéves, alapszakos hallgatója és
Ivanyos János, az ELTE negyedéves matematika alapszakos hallgatója.

Bognár András Károly megoldotta az 1. feladatot, valamint apróbb hiányosságtól eltekintve a 4. és 5. feladatot.

Földesi András megoldotta a 2. és 5. feladatot, valamint fontos részeredményeket ért el az 1. feladatban.

Ivanyos János megoldotta az 2. feladatot, valamint apróbb pontatlanságoktól eltekintve a 1. és 5. feladatot.

Az elsőéves alapszakos hallgatók közül négy feladat lényegében teljes megoldásáért a legjobb elsőévesnek járó oklevelet kap

Duchon Márton Gergő, az ELTE hallgatója.

A versenyen részt vevő diákok emailben kaptak értesítést arról, hogy a megoldásaik közül a bizottság melyeket találta teljesnek vagy lényegében teljesnek, részben megoldottnak, illetve hibásnak.

A versenyfeladatokat és az előzetes megoldásokat a Bolyai Társulat honlapján olvashatják. A korábbi évek feladatai és megoldásai itt találhatók.

További kérdéseket a megoldásokkal kapcsolatban a Ez az e-mail-cím a szpemrobotok elleni védelem alatt áll. Megtekintéséhez engedélyeznie kell a JavaScript használatát. címre írhatnak.

A Matematika Oktatásáért és Kutatásáért Alapítvány járult hozzá a pénzjutalmakhoz.