2024. február 26. és március 2. között 15. alkalommal rendezték meg a Romanian Master of Mathematics (RMM) versenyt, amelyre szokás szerint a magyar csapatot is meghívták. A helyszín, mint a pár covidos évet leszámítva mindig, Bukarest volt, a Tudor Vianu nevét viselő középiskolában.
A versenyen, a Nemzetközi Matematikai Diákolimpiához (IMO-hoz) hasonlóan, a versenyzőknek két egymást követő nap 3-3 feladatot kell megoldaniuk, amire mindkét nap 4 és fél óra áll rendelkezésükre. A feladatok nehézsége is IMO-szintű, sőt előfordul, hogy még nehezebbek. A megszerezhető maximális pontszám most is 42 volt.
A magyar versenyzők eredménye:
Simon László (Budapest, Fazekas Mihály Gimnázium, 12. osztály) 35 ponttal
abszolút 1. helyezést ért el, és ezzel aranyérmet,
Szakács Ábel (Budapest, Fazekas Mihály Gimnázium, 10. osztály) 23 ponttal
bronzérmet,
Varga Boldizsár (Budapest, Veres Péter Gimnázium, 11. osztály) 19 ponttal,
Tarján Bernát (Budapest, Veres Péter Gimnázium, 12. osztály) 15 ponttal
dicséretet kapott.
Köszönjük a Bolyai János Matematikai Társulat segítségét az utazás támogatásában!
Lenger Dániel csapatvezető (Budapesti Fazekas M. Gyak. Ált. Isk. és Gimn. és ELTE)
és Borbényi Márton csapatvezető-helyettes (ELTE és Rényi Intézet)
Következik a diákok rövid beszámolója:
A versenyre vasárnap 15:10-kor indultunk a Keleti pályaudvarról. Életünk legpihentetőbb éjszakája után másnap reggel 9-kor érkeztünk meg Bukarestbe. A pályaudvarról elvittek minket a szállásunkra, ami idén egy 4 csillagos szálloda volt. Kétfős szobákba voltunk beosztva, a csapatvezetők, Berci és Boldi, illetve Ábel és Laci kerültek egy-egy szobába. Ábel és Laci szobája volt a legnagyobb, bár ebben a családias hangulatot egyetlen franciaágy biztosította.
Hétfőn még nem volt hivatalos program, ezért együtt elmentünk Bukarest legnevesebb éttermébe, a főtéren található Burger Kingbe. A délután folyamán jutott eszünkbe, hogy a magyar zászló sajnos otthon maradt, a zászló beszerzésére tett kísérletek határozták meg a következő pár napot. Sajnos a „János bácsi” nevű bolt román eladói nem tudtak nekünk segíteni.
Kedden volt a megnyitó, ahol a helyi iskola diákjai egy zenés műsorral kedveskedtek nekünk. Ezután minden ország egyesével felvonult zászlajával a színpadra, mi jobb híján kölcsön kértük az olaszok zászlóját. A megnyitó után egy, a Jane Street által szervezett Estimathon nevű csapatversenyben vettünk részt Transylvania csapatnévvel, és végül a kínaiakat megelőzve negyedikek lettünk.
Megnyitó egy elfordított olasz zászlóval.
Szerdán következett az első versenynap, ez mindenkinek nagyon jól sikerült, mert három kombinatorika feladat volt 😊. Egy kiadós ebéd után elsétáltunk a Petőfi Sándor és Ady Endre utcák kereszteződéséhez, majd a diadalívhez. Ezután stresszlevezetés céljából meglátogattuk a legközelebbi focipályát. Este Danival és Marcival beszélgettünk a megoldásainkról, hogy számukra könnyebb legyen a másnapi koordinálás.
Séta a Petőfi Sándor és Ady Endre utca sarkán
Csütörtökön a második versenynap már vegyesen sikerült a csapatnak, mert aznap már volt geometria feladat is. A másnapi záróünnepségre viszont még mindig nem volt zászlónk, ezért a zászlóbolt felé vettük az irányt. Háromnegyed óra séta után odaértünk a Google Maps által kijelölt helyre, azonban se közel, se távol nem találtuk a boltot. Nagy elkeseredésünkben a magyar követség felé vettük az irányt, hátha ők tudnak nekünk zászlót adni. Becsöngettünk, de nem keltettünk bennük bizalmat, ezért azt mondták, hogy nincs magyar zászlójuk. Véletlenül hazafele épp útbaesett a focipálya, ezért a vacsora előtt még fociztunk egy jót.
Péntek reggel Marci felhívta a nagykövetséget, és kiderült, hogy mégis van zászlójuk, ezért Marci és Dani elmentek érte. Nem sokkal később pedig kiderült a végeredmény, volt, aki elégedett volt vele, és volt, aki kevésbé. A záróünnepségre büszkén vonultunk frissen szerzett zászlónkkal. Sajnos ezúttal elmaradt a várva várt táncos bemutató. Következett a búcsúvacsora, ahol az előző három napi maradékokat szolgálták fel, ennek ellenére mindenki nagyon jól lakott.
A magyar csapat érmekkel és a magyar zászlóval
Szombat reggel még a szállodában reggeliztünk, bevásároltunk helyi nyalánkságokból, az ebédre már a pályaudvaron került sor, a McDonalds-ban vagy a KFC-ben kinek-kinek ízlése szerint. Következett a már jól ismert 16 órás vonatút, azzal a különbséggel, hogy most hajnali 2-kor keltettek minket a határon. Vasárnap hajnali 5-kor érkeztünk meg a Keleti pályaudvarra, elbúcsúztunk egymástól, és – hazamentünk aludni.
És akkor pár szó a feladatokról (amelyek megtalálhatók itt):
Az 1. feladat egy kevésbé nehéz kombinatorika feladat volt, egy nagy sakktáblán kellett futókat mozgatni úgy, hogy mindig pontosan egy teljes sort foglaljanak el. A kérdés az volt, hogy hányféle sorrendben lehetnek a futók ilyen mozgatások után.
A 2. feladat egy olyan számelmélet feladat volt, ahol az ötlet (hogy mindig mohón válasszuk azt a maradékosztályt, amelyből a legtöbb van) elég kézenfekvőnek tűnt, azonban a kidolgozása nem volt triviális. Az viszont egyikünknek se tetszett, hogy a „minden második lépésben tudunk abból a maradékosztályból választani, amiből a legtöbb van” ötlet megoldja a feladatot az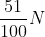 
helyett
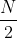-vel, és ezen szinte jelentéktelen élesítéshez így még egy ötletet be kellett vetni (szerencsére a csapatból így is mindenki megoldotta ezt a feladatot).
A 3. feladat egy nehéz, egyetlen adott témakörbe nehezen besorolható feladat volt. Az elején geometriának látszó állítást ügyesen át lehetett fogalmazni kombinatorikussá, és végül lineáris algebrával vagy egy nehezebb tétellel lehetett befejezni a feladatot.
A 4. számelméleti feladat mint kiderült, inkább algebra volt. A megoldása viszonylag rövid, ennek ellenére nehéz volt rájönni.
Az 5. egy nem szokványos, elég nehéz geometria példa volt, mozgó körökről kellett belátni, hogy két fixpontban metszik egymást. Megsejthető volt, hogy a fixpontok szabályos háromszöget alkotnak az adott két csúccsal, és ezt sokféleképpen lehetett bizonyítani.
A 6. egy nagyon nehéz algebra feladat volt, a 0,1 együtthatós négyzetmentes polinomokról szólt, az egész mezőnyből csak egy online résztvevő tudta megoldani.