Társulati díjak 2021

Szele Tibor Emlékérem

A 2021. évi Szele Tibor Emlékérem kitüntetettje Némethi András, az MTA levelező tagja, a Rényi Alfréd Matematikai Kutatóintézet tudományos osztályvezetője, az ELTE egyetemi tanára, aki az algebrai geometriában és a differenciáltopológiában, ezen belül különösen a szingularitáselméletben ért el kimagasló tudományos eredményeket. Ezen témaköröket Magyarországon úttörőként művelte és terjesztette el. Kutatásai mellett kiemelkedik fáradhatatlan iskolateremtő munkája és a kimagasló utánpótlást nevelő munkássága is. A teljes indoklást itt olvashatják.

A díjról és a korábbi évek díjazottairól a https://www.bolyai.hu/dijaink-szele-tibor-emlekerem oldal tájékoztat.

Grünwald Géza Emlékérem

2021-ban a Grünwald Géza Emlékéremre öt felterjesztés érkezett. Egyhangú döntéssel, a Bizottság mindnyájukat méltónak találta a kitüntetésre. Így a 2021-es díjazottak listája: Kunosné Nedényi Fanni, Maga Balázs, Nagy János, Poór Márk és Remete László. A részletes jelentés itt olvasható.

A díjról és a korábbi évek díjazottairól a https://www.bolyai.hu/dijaink-grunwald-geza-emlekerem oldal tájékoztat.

Farkas Gyula Emlékdíj

Ebben az évben a Farkas Gyula Emlékdíjat az alkalmazott matematikában kiemelkedő tudományos eredményeket elérő négy fiatal matematikus: Balázs István, Boldog Péter, Lovas Attila és Varga Bálint kapták meg. A díjazottak munkásságát itt ismertetjük.

A díjról és a korábbi évek díjazottairól a https://www.bolyai.hu/dijaink-farkas-gyula-emlekdij oldal tájékoztat.

Rényi Kató Emlékdíj

2021-ben 10 felterjesztés is érkezett kiváló, önálló tudományos eredményt elért 25 év alatti fiatalokra. Közülük csak 4 kaphatta meg a Rényi Kató Emlékdíj 1.fokozatát: Borbényi Márton, Imolay András, Keliger Dániel és Pálfy Máté. A részletes jelentés és indoklás itt tekinthető meg.

A díjról és a korábbi évek díjazottairól a https://www.bolyai.hu/dijaink-renyi-kato-emlekdij oldal tájékoztat.

Patai-díj

A Patai Alapítvány 2021. évi díját Torma Gábor részére ítélte oda a Bizottság az alábbi indoklással.

Torma Gábor 2013 és 2019 közt a Szegedi Tudományegyetem Természettudományi Karán fizika-matematika osztatlan tanár szakán tanult, 2019 óta a Matematika és Számítástudományi Doktori Iskola didaktika alprogramjának ösztöndíjas hallgatója. 2018 óta a szegedi Dugonics András Piarista Gimnázium matematika-fizika tanára. Emellett 2016 óta oktat a Szegedi Tudományegyetemen. A tehetséges fiatal tanár-kutató tanárként meggyőző erővel tartott előadásaival szeretteti meg középiskolás és egyetemi diákjaival a matematikát. Ennek érdekében a legmodernebb informatikai és módszertani eszközöket alkalmazza, azokat továbbfejleszti, önálló kutatásokat végez. Eredményeiről publikációkban, konferencia előadásokon számol be.

A 2020. márciusában ránk tört, s hullámokban azóta is vissza-visszatérő online oktatásban példamutató módon, több saját innováció alkalmazásával állta meg helyét, bizonyítva ezzel is pályára való alkalmasságát, tanári és kutatói rátermettségét. A tapasztalatokat közös cikk, illetve a cikkhez kapcsolódóan tudományos-továbbképző előadás formájában osztotta meg a széles körű szakmai közösséggel.

Szakmai közéleti tevékenysége kiemelkedő. 2013 óta folyamatosan a szegedi Eötvös Kollégium különböző szakmai műhelyeinek aktív tagja, jelenleg a pedagógus műhely titkára, programok lelkes szervezője. 2018 óta a Medve Szabadtéri Matematikaverseny önkéntese. Egyetemi projektek keretében vállalta tutorként alsóbb éves hallgatók tanulmányainak és elsőéves hallgatók tudásszintmérésének segítését is. Torma Gábor munkásságának értékét a számára odaítélt SZTE TTIK Kiváló Hallgatója, Talent Ösztöndíj és a Nemzeti Felsőoktatási Ösztöndíjak is minősítik.

A díjról és a korábbi évek díjazottairól a https://www.bolyai.hu/dijaink-patai-dij oldal tájékoztat.

A 2021. évi Schweitzer Miklós Matematikai Emlékversenyről

A Bolyai János Matematikai Társulat 2021. október 22. és november 2. között rendezte meg a 2021. évi Schweitzer Miklós Matematikai Emlékversenyt. A versenyen középiskolai tanulók, egyetemi és főiskolai hallgatók, valamint 2021-ben egyetemet vagy főiskolát végzettek vehettek részt.

A Bolyai János Matematikai Társulat a verseny megrendezésére a következő bizottságot kérte fel: Páles Zsolt (elnök), Nagy Gergő és Pink István (titkárok), Baran Sándor, Bérczes Attila, Bessenyei Mihály, Boros Zoltán, Fazekas István, Figula Ágota, Gát György, Győry Kálmán, Hajdu Lajos, Muzsnay Zoltán, Novák-Gselmann Eszter, Tengely Szabolcs, Vincze Csaba.

A versenybizottság 10 feladatot tűzött ki. A feladatokat Buczolich Zoltán, Fazekas István, Gát György, Hajdu Lajos (2 feladat), Páles Zsolt (2 feladat),Totik Vilmos (2 feladat) és Vincze Csaba bocsátotta a bizottság rendelkezésére. A feladatok és a megoldások itt érhetők el.

A versenyre 9 versenyző 40 megoldást nyújtott be, melyek közül 29 volt hibátlan. Az alábbi táblázatban pontok jelzik, hogy a versenyzők mely feladatokra nyújtottak be megoldásokat.

	1	2	3	4	5	6	7	8	9	10
Borbényi Márton	$\bullet$	$\bullet$	$\bullet$	$\bullet$	$\bullet$	$\bullet$			$\bullet$	$\bullet$
Füredi Erik	$\bullet$	$\bullet$		$\bullet$					$\bullet$	$\bullet$
Gárgyán Barnabás		$\bullet$
Gáspár Attila	$\bullet$	$\bullet$	$\bullet$	$\bullet$	$\bullet$	$\bullet$				$\bullet$
Imolay András	$\bullet$	$\bullet$		$\bullet$					$\bullet$	$\bullet$
Iványos János Balázs		$\bullet$
Kovács Benedek	$\bullet$	$\bullet$	$\bullet$						$\bullet$	$\bullet$
Seress Dániel		$\bullet$			$\bullet$				$\bullet$	$\bullet$
Tóth Péter	$\bullet$				$\bullet$				$\bullet$	$\bullet$

A megoldások értékelése után a versenybizottság a következő döntést hozta.

I. díjban részesül Gáspár Attila, az ELTE elsőéves Matematikus MSc hallgatója

II. díjban részesül Borbényi Márton, az ELTE másodéves Matematikus MSc hallgatója

III. díjban részesül Füredi Erik, az ELTE elsőéves Matematika BSc hallgatója, Kovács Benedek, az ELTE másodéves Matematikus MSc hallgatója és Tóth Péter, a DE másodéves Alkalmazott matematikus MSc hallgatója

Indoklás

Gáspár Attila 7 feladatra nyújtott be megoldást; mindegyikre adott megoldása teljes, a 3. feladatra adott megoldásának 1. része újszerű. Megoldásai nagyon színvonalasak, az 5., 6. és 10. feladat esetén a versenybizottság azokat választotta mintamegoldásnak.

Borbényi Márton 8 feladatra nyújtott be megoldást; az 1., 3., 4., 6., 9. és 10. feladatokra adott megoldása teljes; a 2. és 5. feladatra adott megoldása hiányos, de javítható.

Füredi Erik 5 feladatra nyújtott be megoldást; a 2., 4., 9. és 10. feladatokra adott megoldása teljes; az 1. feladatnak csak az egyik részére adott megoldása helyes.

Kovács Benedek 5 feladatra nyújtott be megoldást; mindegyikre adott megoldása teljes.

Tóth Péter 4 feladatra nyújtott be megoldást; mindegyikre adott megoldása teljes.

A 2021. évi Kürschák József Matematikai Tanulóversenyről

A Bolyai János Matematikai Társulat a 2021. évi Kürschák József Matematikai Tanulóversenyt október 8-án rendezte meg. A Társulat elnöksége a verseny lebonyolítására az alábbi bizottságot kérte fel: Biró András, Frenkel Péter, Harangi Viktor, Kós Géza, Maga Péter (titkár), Pach Péter Pál (elnök), Tóth Géza.

A bizottság a következő feladatokat tűzte ki:

1. A síkbeli derékszögű koordinátarendszer 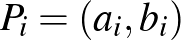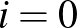$P_i=(a_i, b_i)$ ( $i=0$ , 1, 2) pontjai által alkotott háromszögnek az 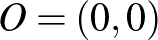$O=(0,0)$ origó belső pontja. Mutassuk meg, hogy a 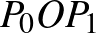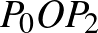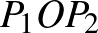$P_0OP_1$ , $P_0OP_2$ , $P_1OP_2$ háromszögek területei (ebben a sorrendben) akkor és csak akkor alkotnak mértani sorozatot, ha az

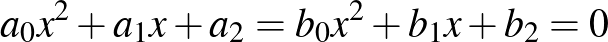
$\displaystyle a_0x^2+a_1x+a_2=b_0x^2+b_1x+b_2=0$

egyenletrendszernek van valós 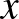$x$ megoldása.

2. Csodaország 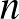$n$ városa között 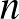$n$ légitársaság üzemeltet járatokat. Minden egyes légitársasághoz páratlan sok város tartozik, mondjuk 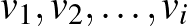$v_1,v_2,\ldots,v_i$ , amelyek között körjáratot üzemeltet mindkét irányban: a 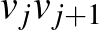$v_jv_{j+1}$ illetve a 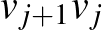$v_{j+1}v_j$ járatokra lehet jegyet váltani 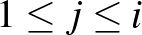$1\le j\le i$ esetén, ahol 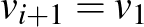$v_{i+1}=v_1$ . Igazoljuk, hogy található páratlan sok város, mondjuk 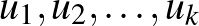$u_1,u_2,\ldots,u_k$ úgy, hogy az 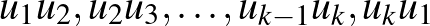$u_1u_2,u_2u_3,\ldots,u_{k-1}u_k,u_ku_1$ járatokra lehet jegyet váltani csupa különböző légitársaságnál.

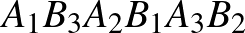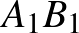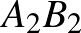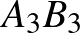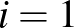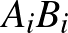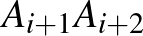3. Adott az $A_1B_3A_2B_1A_3B_2$ húrhatszög, amelynek $A_1B_1$ , $A_2B_2$ és $A_3B_3$ átlói egy ponton mennek át. Minden $i=1$ , 2, 3 esetén az $A_iB_i$ és az $A_{i+1}A_{i+2}$ átlók metszéspontja 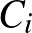$C_i$ , továbbá 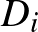$D_i$ olyan, a 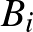$B_i$ -től különböző pont a hatszög köré írt körön, amelyre a 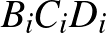$B_iC_iD_i$ kör érinti az 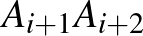$A_{i+1}A_{i+2}$ egyenest. 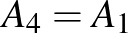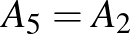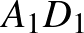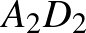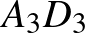(A pontokat modulo 3 számozzuk, tehát $A_4=A_1$ és $A_5=A_2$ .) Igazoljuk, hogy az $A_1D_1$ , $A_2D_2$ és $A_3D_3$ szakaszok egy ponton mennek át.

Az idei versenyen a 78 regisztrált versenyző közül 73-an vettek részt a versenyen, és tőlük összesen 64 dolgozat érkezett be. Az első feladatot 21-en, a második feladatot 5-en, a harmadik feladatot pedig 3-an oldották meg helyesen vagy lényegében helyesen. Bár mindegyik feladatra születtek helyes megoldások, két feladatnál többet egyetlen versenyző sem oldott meg, így a versenybizottság idén nem adott ki I. díjat.

Egy versenyző helyesen oldotta meg az első és a harmadik feladatot. Ezért

II. díjban és 50 000 Ft pénzjutalomban részesült

Seres-Szabó Márton, a Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium 11. osztályos tanulója (tanárai Dobos Sándor, Ádám Réka és Fazakas Tünde).

III. díjban és 40 000 Ft pénzjutalomban részesült

Fleiner Zsigmond, a Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium 12. osztályos tanulója (tanárai Hujter Bálint, Gyenes Zoltán, Dobos Sándor és Juhász Péter), aki javítható hibától eltekintve helyesen oldotta meg az első feladatot és kis hiányossággal oldotta meg a második feladatot,

Várkonyi Zsombor, a Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium érettségizett tanulója (tanárai Fazakas Tünde, Kocsis Szilveszter, Pósa Lajos és Dobos Sándor), aki lényegében helyesen oldotta meg az első feladatot és helyes megoldást adott a második feladatra.

Dicséretben és 20 000 Ft pénzjutalomban részesült

Csaplár Viktor, a Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium érettségizett tanulója (tanárai Fazakas Tünde és Kocsis Szilveszter), aki apró hiányosságtól eltekintve helyesen oldotta meg az első feladatot és részeredményeket ért el a harmadik feladatban.

A versenybizottság ezúton köszöni meg minden versenyző, felkészítő tanár és a lebonyolításban közreműködő kolléga munkáját, a díjazottaknak pedig további sikereket kívánva gratulál.

A feladatok megoldásai megjelentek a KöMaL 2022. februári számában.