1. Életrajza
Calyampudi Radhakrishna (C. R.) Rao 1920 szeptember 10-én született Huvanna Hadagaliben, India déli részén (az egykori Madras körzetében). Egy tízgyermekes család nyolcadik gyermeke volt, és akkori szokás szerint a nyolcadik gyerek Krisna istenség után kapta egyik nevét. Apja éles eszű rendőrfelügyelő és nyomozó volt, a család gyakran költözött. Édesanyja korán felismerte fia tehetségét, aki már ötévesen 16 x 16 -ig fejben szorzott össze villámgyorsan számokat (16 volt a váltószám a rúpia és kisebb egységei közt). Így ötévesen rögtön a második osztályba íratták be, és édesanyja reggelente négy órakor felkeltette, hogy friss fejjel, olajmécsesnél nyugodt körülmények közt tanulhasson, Rao pedig örömmel vállalta a leendő tudós szerepét a családban; tíz éve mesélte, hogy még mindig dolgozik reggelente és ehhez olajmécsest gyújt. (Egyéb tehetségek is voltak a családban: egyik bátyjából jó memóriájáról híres anatómiaprofesszor, egyik lánytestvéréből pedig ismert indiai költőnő vált.) Tizenhét évesen Rao már az Andhra Egyetem (Andhra Pradesh) diákja volt, ahol előbb BA, majd húszévesen MA fokozatot szerzett matematikából. Sokat köszönhetett Cambridge-ben végzett tanárának (V. Ramaswami) és a Mathematics Student című újságnak, mely feladatokat tűzött ki, és Rao büszkén látta, hogy több feladatmegoldása is megjelent ott. Ezek után természetesnek találta, hogy kutatói ösztöndíjra pályázzon és doktorátust szerezzen, de ez nem ment olyan könnyen, mint gondolta. Elsőre nem vették fel. (Azt mondták, elkeveredtek a papírjai, de lehet, hogy származását nem tartották megfelelőnek. A kasztrendszerben családja nem foglalt el előkelő helyet; egy visszaemlékezésében írt is arról, hogy a brahminok gyerekei, akiket iskolás korában korrepetált, nem engedték inni a vizükből; Indiában ui. nem minden víz iható, az ivóvíznek kiemelt jelentősége van.)
1940-1941 fordulóját írták Indiában, ami ekkor még brit koronagyarmat volt (alkirállyal), és dúlt a II. világháború. Rao olvasta az újságban, hogy Kalkuttában jelentkezőket keresnek egy gyors katonai kiképzésre, ami valamiféle hadmérnöki képesítést ad, és akik azt elvégzik, az afrikai hadszíntéren fognak elsősorban műszaki feladatokat teljesíteni. Mivel a fizika és műszaki alkalmazások is közel álltak hozzá, és megélhetéséhez munkára volt szüksége, gondolta, hogy jelentkezik erre. Életében először utazott Kalkuttába (Kalkutta 2001-től visszavette régi nevét, most Kolkatának hívják); napokig tartott a vonatút, mezítláb utazott, egyetlen jó cipőjét csomagjában vitte a felvételire. Azonban ott sem járt sikerrel: katonai pályára alkalmatlannak minősítették, elsősorban gyenge fizikuma miatt. Nem akart csak úgy visszamenni falujába, hanem ellátogatott az Indian Statistical Institute-ba (Indiai Statisztikai Intézet, továbbiakban ISI). Ott rögtön elismerték matematikai képességeit, hamarosan találkozott Prof. P. C. Mahalanobisszal is, és 1941 januárjától már az első MA fokozatot adó statisztika-évfolyamon tanult (öten kezdtek ott); 1943-ban megszerezte második master fokozatát, és kisebb megszakításokkal 40 évig Kalkuttában maradt. Rao a véletlen művének tekintette, hogy a statisztikával kapcsolatba került, ami egyébként is a véletlenek tudománya.
Néhány szót kell ejtenünk az ISI-ről és az indiai statisztikáról. A britek már 1892-től bevezették Indiában a rendszeres népességnyilvántartást, ami nem csak születési és halálozási adatokat tartalmazott közigazgatási egységenként, hanem egészségügyi és oltási adatokat is (már ekkor voltak kötelező oltások a gyerekeknek). A függetlenedési folyamat részeként indiai politikusok (pl. Minoo Masani) 1938-ban kezdeményezték egy National Planning Committee megalakítását, ami elsősorban gazdasági kérdésekkel foglalkozott. A függetlenedés (1947) után egyéb kormányszintű bizottságok is alakultak, pl. 1951-ben a National Income Committee, aminek Mahalanobis, az ISI igazgatója volt kezdetben a vezetője. A későbbiekben is kikérte a minisztérium a statisztikusok véleményét a fontosabb pénzügyi kérdésekben, így pl. Rao is többször megfordult a minisztériumban, amikor az ISI igazgatója volt. Miután a statisztika (eleinte csak az adatgyűjtést és feldolgozást értették alatta) fontos szerepet kapott Indiában, Mahalanobis, a Cambridge-ben végzett fizikus 1931-ben Kalkuttában megalapította az ISI-t, ahol alapvetően klasszikus természettudományokat oktattak, de Mahalanobis igyekezett az új európai és amerikai eredményeket is felvenni a tananyagba (R. A. Fisher, K. Pearson, J. Neyman, Á. Wald, N. A. Kolmogorov és a svéd H. Cramér ma is tanított tételei ekkor, a klasszikus statisztika fénykorában születtek). Így alakult meg 1941-ben az új statisztika szakirány, amit Rao is elvégzett 1943-ra. Ezután tanársegéd lett az ISI-ben, ahol valójában ő állította össze a statisztika szakirány képzéséhez a tananyagot, amiben sok hiányosságot tapasztalt. Úgy gondolta, jó tanárként neki kell pótolnia ezeket. Így pl. egyik diákja kérdésére, hogy mennyire vihető le a torzítatlan becslések szórása, másnap válaszolni akart. Ezért 1944 őszén egy éjszaka alatt hibaszámítási módszerekkel kihozta azt az eredményt, amit ma Cramér-Rao egyenlőtlenségként tanítunk. Cramér 1945 tavaszán kapta hasonló eredményeit, és a már létező Fisher-információval kapcsolatba hozva közös eredményként tartják számon a tételt. Ezt a tételét másik áttörő (D. Blackwellel közös) eredményével együtt egy mindössze 10 oldalas cikkben publikálta a Bulletin of Calcutta Mathematical Society-ben, 1945-ben. Megjegyezzük, hogy az ISI-nek később több tagozata is alakult, Delhiben, Bombayben (ma Mumbai) és Bangalore-ban.
1946 és 1948 között Rao a cambridge-i egyetemen dolgozott, ugyanis az ottani Antropológiai és Archeológiai Múzeum számára brit régészek a Jebel Maya törzs csontmaradványait hozták el Észak-Afrikából, és az egyetem Mahalanobis segítségét kérte a maradványok többváltozós statisztikai analíziséhez. Ehhez a Mahalanobis-féle 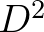 távolságot akarták használni, és egyéb szakmai segítséget is kértek. Mahalanobis Raot küldte ki erre a feladatra Cambridge-be, ahol Rao megismerkedett és együtt dolgozott az angolszász statisztikai iskola megalapítójával és akkori vezetőjével, Sir R. A. Fisherrel. Meglévő és ott elért eredményei alapján az eltöltött két év alatt PhD fokozatot szerzett. Doktori értekezésének fő témája a varianciaanalízis többdimenziós általánosítása (MANOVA) volt, amit biológiai és az említett régészeti adatokon is alkalmazott. Tíz éve Rao tréfásan megjegyezte, hogy ő volt Fisher egyetlen fokozatot szerzett PhD hallgatója, ugyanis a bogaras professzornak az volt az elve, hogy a diáknak magának kell megtalálnia a témát és azt önállóan is kell feldolgoznia, ő maga csak a légkört és a helyszínt (ún. laboratóriumát) biztosítja hozzá. Rao azt is megjegyezte, hogy ő maga is próbálkozott ezzel a módszerrel, de nem sok sikerrel. Végülis rengeteg időt töltött a nála végzett 50 PhD diákkal, akik közül az első D. Basu volt (akinek elégséges és teljes statisztikákról vannak fontos tételei), és köztük volt a későbbi Abel-díjas S. R. S. Varadhan is. Mikor 90. születésnapja körül megkérdezték, mely eredményeire a legbüszkébb életében, ezt válaszolta: „it is the outstanding contributions my students are making to statistical theory and practice” (diákjaim kiemelkedő eredményeire, amelyek a statisztika területén születnek, úgy az elméletében, mint az alkalmazásokban). Később Rao DSc fokozatot is kapott Cambridge-ben (addigi cikkei alapján), és ezzel az ún. Life Fellow of King's College Cambridge címet is elnyerte (aminek fontos következménye volt, hogy fűre léphetett az egyetem területén, mint ezt viccesen meg is jegyezte egy visszaemlékezésében).
távolságot akarták használni, és egyéb szakmai segítséget is kértek. Mahalanobis Raot küldte ki erre a feladatra Cambridge-be, ahol Rao megismerkedett és együtt dolgozott az angolszász statisztikai iskola megalapítójával és akkori vezetőjével, Sir R. A. Fisherrel. Meglévő és ott elért eredményei alapján az eltöltött két év alatt PhD fokozatot szerzett. Doktori értekezésének fő témája a varianciaanalízis többdimenziós általánosítása (MANOVA) volt, amit biológiai és az említett régészeti adatokon is alkalmazott. Tíz éve Rao tréfásan megjegyezte, hogy ő volt Fisher egyetlen fokozatot szerzett PhD hallgatója, ugyanis a bogaras professzornak az volt az elve, hogy a diáknak magának kell megtalálnia a témát és azt önállóan is kell feldolgoznia, ő maga csak a légkört és a helyszínt (ún. laboratóriumát) biztosítja hozzá. Rao azt is megjegyezte, hogy ő maga is próbálkozott ezzel a módszerrel, de nem sok sikerrel. Végülis rengeteg időt töltött a nála végzett 50 PhD diákkal, akik közül az első D. Basu volt (akinek elégséges és teljes statisztikákról vannak fontos tételei), és köztük volt a későbbi Abel-díjas S. R. S. Varadhan is. Mikor 90. születésnapja körül megkérdezték, mely eredményeire a legbüszkébb életében, ezt válaszolta: „it is the outstanding contributions my students are making to statistical theory and practice” (diákjaim kiemelkedő eredményeire, amelyek a statisztika területén születnek, úgy az elméletében, mint az alkalmazásokban). Később Rao DSc fokozatot is kapott Cambridge-ben (addigi cikkei alapján), és ezzel az ún. Life Fellow of King's College Cambridge címet is elnyerte (aminek fontos következménye volt, hogy fűre léphetett az egyetem területén, mint ezt viccesen meg is jegyezte egy visszaemlékezésében).
1948 több szempontból is fordulópontot jelentett Rao életében. Hazatért Cambridge-ből, és az ISI-ben hamarosan professzornak nevezték ki (29 évesen). Később az ottani Research and Training School igazgatója lett (1964–1972), majd Mahalanobis halála után az ISI igazgatója (1972–1976). 1980-ban, 60 évesen nyugdíjba kellett vonulnia, de ekkor új karriert kezdett az USA-ban. Egy-két évet (nem összefüggő módon) már töltött előzőleg az USA egyetemein (University of Illinois, John Hopkins University, Indiana University, Ohio State University, Stanford University), de 1980-tól a University of Pittsburgh, majd a Pennsylvania State University állandó professzora lett, sőt utóbbinak ma is emeritus professzora. (80 éves kora után már nem taníthatott, de a Többváltozós Statisztika Központ vezetőjeként még sokáig foglalkozott a Pennsylvania State Universityn diákokkal.) Fontos (talán hosszú élete szempontjából is), hogy Rao megosztotta az évet India és az USA közt: az áprilistól októberig tartó időszakot töltötte az USA-ban, a másik félévet pedig Indiában. Az ezredforduló után megkezdte egy intézet létrehozását Hyderabadban, nem túl messze szülőhelyétől. Hyderabad egyébként is fontos természettudományos központtá vált, Microsoft székhely, stb. Hosszú évek erőfeszítésével megalapította a CR Rao Advanced Institute of Mathematics, Statistics and Computer Science (AIMSCS) intézetet a University of Hyderabad Campus területén. Az intézet fokozatosan bővült épületekkel, amihez az indiai kormánytól is kapott támogatást. Közben a pénz elfogyott, pedig Rao még egy statisztikamúzeumot is létesíteni akart. Ehhez végül is felesége, Bhargavi nyújtott támogatást saját vagyonából (rögtön írok bővebben erről a nagyszerű asszonyról); így 2013-ban avatták fel a Galleryt, a világ első statisztika múzeumát.
Az 1948-as év Rao magánéletében is fordulatot hozott: ekkor vette feleségül Bhargavit a Bengáli-öböl partján Hyderabadtól délkeletre fekvő Chennai-ban (egykor Madras). Ide később is gyakran járt „nyaralni” januárban a család. (Madras a Brit Kelet-Indiai Társaság székhelye volt a XVIII. századtól, de az 1858-as szipojfelkelés következtében azt felszámolták.) Bhargavi híresen okos lány volt, aki Rao szülőfaluja környékéről származott, történelemből és közgazdaságtanból szerzett MA fokozatot. Szülei azt gondolták, hogy félénk és állandóan tanuló lányuk soha nem fog férjhez menni, de Rao édesanyja nem így gondolkodott: összeismertette Cambridge-ből hazatérő fiával, amiből hamarosan házasság lett. Bhargavi attól kezdve mindenhová követte férjét, matematikai konferenciákra utazott és maga is elsajátította és használta a többváltozós statisztikai módszereket szociológiai, gazdasági és pszichológiai alkalmazásokban. Pszichológiát Kalkuttában kezdett tanulni, az USA-ban pedig mester fokozatot szerzett belőle, és tanított, dolgozott is pszichológusként. Valószínűleg ezzel szerezhette magánvagyonát, amiről férje meglepetéssel értesült, amikor azt felajánlotta az AIMSCS építkezések céljaira (nem csekély összeg volt, összemérhető a kapott állami támogatással). Bhargavival tíz éve én is találkoztam Hyderabadban. Látszott, hogy nagyon nyitott az emberek iránt, minden érdekelte a világról, éppen szerbiai útra készülődött férjével. Alig voltak az arcán ráncok. Sajnos már nincs közöttünk, 92 évet élt; 2017-ben bekövetkezett halála után ösztöndíj viseli a nevét (amit megmaradt vagyonából alapított). Az 1950-es években két gyerekük is született. Elsőnek egy lány, Tejaswini, aki PhD fokozatot szerzett táplálkozástudományból a Pennsylvania State Universityn, jelenleg a buffalói Dietetics and Nutrition Department of the SUNY College professzora. (Most Rao nála él, és neki is van kapcsolata az ottani egyetemmel.) Tejaswini a klasszikus indiai táncoknak is hódol, nemcsak táncol, hanem a Natya nevű tánciskola igazgatója Buffalóban. (Megjegyzem, hogy Rao is szereti az indiai táncokat. Amikor egy időre az ISI Delhi-beli tagozatában dolgozott, rosszallotta, hogy ott nem ismerik a Kalkuttában elterjedt indiai táncokat. Ezért ő is alapított egy tánciskolát Delhiben, amit támogatott saját jövedelméből, legalábbis, amíg ott tartózkodott.) Második gyermekük fiú (Veerendra), villamosmérnök és számítástudós. Egy számítástechnikai tanácsadó vállalkozást vezet Pittsburgben. Neki két fia van.
2. Publikációk és áttörő eredmények
C. R. Rao 16 könyv és 350 tudományos cikk szerzője. Két legolvasottabb könyvét számtalan nyelvre lefordították. Ezek:
- Linear Statistical Inference and its Applications, John Wiley, first edition: 1965, second edition: 1973. Az Amazon.com a „Must-have statistics books” között listázza (nélkülözhetetlen statisztika könyv), ami egy recenzorának szavaival „information packed book, bible of matrix and linear theory in stat” (információval teli könyv, a statisztika mátrixos és lineáris elméletének bibliája.).
- Statistics and Truth, World Scientific, first edition: 1989, second edition: 1997. A neves statisztikus, Sir David Cox írta róla: „The book is a powerful illustration of the nature of statistical arguments and I can think of no better book to introduce the subject, in particular to a general reader.” (A könyv kiválóan illusztrálja a statisztikai következtetések
természetét, és nem tudok jobb könyvet elképzelni a tárgy bevezetésére, különösen a laikus olvasónak.)
Első cikke: Information and Accuracy Attainable in the Estimation of Statistical Parameters, Bulletin of Calcutta Mathematical Society 37, pages 81–91 (1945). A cikk másodkiadásban megjelent a Breakthroughs in Statistics 1890–1990, Springer-Verlag kötetben, egyéb ifjúkori cikkeivel együtt (közöttük jelent meg pl. a Rao Score Test).
Statisztika, biometria, ökonometria könyvekben megjelenő szakkifejezések, amelyeket cikkei nyomán vezettek be: Cramér–Rao egyenlőtlenség, Rao–Blackwellizáció, Fisher–Rao tétel, Rao ortogonális tömbök, többváltozós varianciaanalízis (MANOVA), kanonikus korrelációanalízis, mátrixok általánosított inverze.
További fogalmak, amelyek az övéiből nőttek ki: kvantum Cramér–Rao határ (élesebb becslést ad a Heisenberg-elvre kvantumfizikában); spektrális és szinguláris felbontás egységes használata a többváltozós statisztikában; kombinatorikus módszerek a kísérlettervezésben és új, nemlineáris módszerek. Ezzel kapcsolatos új publikációk (az utolsó kettő most fog megjelenni):
- G. J. Babu, C. R. Rao, Bootstrap methodology. Handbook of Statistics, Vol 9, pp. 627-659, Elsevier (1993).
- B. B Pereira, C. R. Rao, F. B. Oliveira, Statistical Learning and Neural Networks. A Guide for Statisticians and Data Scientists with Python. Handbook of Statistics, CRC Press, Taylor and Francis Group (2020).
- A. S. Rao, C. R. Rao eds.: Principles and Methods for Data Science. Handbook of Statistics 43, North Holland, Elsevier (2020).
3. Közéleti tevékenység, kitüntetések
A II. világháború után C. R. Rao egy ENSZ-bizottság elnöke volt, amelynek célja egy ázsiai országokra kiterjedő statisztikai intézet megalakítása volt; Tokióban meg is alakult a Statistical Institute for Asia and Pacific. Megalapította az Indian Econometric Societyt és az Indian Society for Medical Statisticset. Elnöke volt olyan nemzetközi statisztikai egyesületeknek, mint az International Statistical Institute, Institute of Mathematical Statistics, USA és az International Biometric Society. Azon túl, hogy 18 országban kapott tiszteletbeli doktori címet, a következő indiai és nemzetközi kitüntetések birtokosa:
- Shanti Swarup Bhatnagar Award of the Indian Council of Scientific and Industrial Research – Nehru miniszterelöktől vette át 1963-ban. Rao a teljes pénzösszeget a National Defense Fund számára adta át támogatásként, mondván, hogy: „The country's need is greater than mine” (az országnak nagyobb szüksége van rá, mint nekem).

C. R. Rao átveszi Nehrutól a kitüntetést, de az indiai államnak adja a pénzjutalmat.
- National Medal of Science, USA – 2002-ben G. W. Bush amerikai elnöktől kapta, aki egy új kor prófétájának nevezte Raot („a prophet of new age”).
- India Science Award – az Indiai Tudományért Kitüntetés, amelyet India miniszterelnöke adott át neki 2009-ben a statisztikai tudományokban hat évtizedes példaértékű munkássága során tett jelentős hozzájárulásaiért („for his significant contributions to the field of statistical science during an illustrious career spanning six decades”).
- Guy Medal in Gold of the Royal Statistical Society, Az Egyesült Királyság Királyi Statisztikai Társaságának Guy-aranyérme 2011-ben; a statisztika elméletéhez és módszertanához tett olyan jelentős hozzájárulásaiért, mint a minimális szórású torzítatlan becslések, elégséges statisztikák, információs geometria, továbbá a mátrixelmélet alkalmazása a lineáris statisztikai következtetések terén. („For his fundamental contributions to statistical theory and methodology, including unbiased estimation, variance reduction by sufficiency, efficiency of estimation, information geometry, as well as the application of matrix theory in linear statistical inference”). Ezt a William Guy által alapított díjat háromévente adományozzák. Van ezüst és bronz fokozat is. Az ezüst fokozatot C. R. Rao már megkapta 1965-ben. 1892 óta ő volt a harmincnegyedik, aki átvehette az arany fokozatot, amit előzőleg olyanok kaptak, mint R. A. Fisher (1946), E. S. Pearson (1955), J. Neyman (1966), M. S. Bartlett (1969), H. Cramér (1972) és D. Cox (1973). Közülük csak H. Cramér és J. Neyman nem volt brit. C. R. Rao az első nem európai és nem amerikai, aki ezt az elismerést kapta.
4. Egy kis matematika
A Cramér–Rao egyenlőtlenség (bizonyos regularitási feltételek mellett) egységes alsó korlátot ad egy paraméterfüggvényre nézve torzítatlan becslések szórásnégyzetére (ill. kovariancia-mátrixára, többdimenziós paramétertér esetén). A korlátban szerepel az ún. Fisher-információs mátrix, amely csupán a paraméter függvénye, és az adott (reguláris) eloszlásból kiszámolható (kapcsolata van Shannon-entrópiával is). Néhány fogalom és jelölés szükséges a tétel megfogalmazásához anélkül, hogy túl technikai lennék.
Legyen 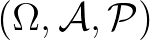 dominált, identifikálható, paraméteres statisztikai mező,
dominált, identifikálható, paraméteres statisztikai mező, 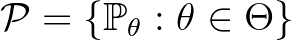 eloszláscsalád; továbbá
eloszláscsalád; továbbá 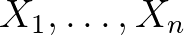 (egy- vagy többdimenziós) független, azonos eloszlású (fae) minta a
(egy- vagy többdimenziós) független, azonos eloszlású (fae) minta a 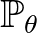 eloszlásból, ahol
eloszlásból, ahol 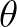 ismeretlen paraméter, ami a
ismeretlen paraméter, ami a 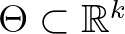 nyílt (konvex) paramétertérben van. Célunk az ismeretlen paraméter valamely
nyílt (konvex) paramétertérben van. Célunk az ismeretlen paraméter valamely 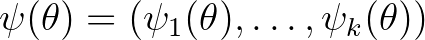 függvényének torzítatlan becslése, ahol
függvényének torzítatlan becslése, ahol 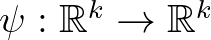 bijektív, differenciálható függvény (gyakran az identitás, amikor is magát
bijektív, differenciálható függvény (gyakran az identitás, amikor is magát 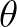 -t becsüljük). A becsléselmélet alapfeladata, hogy a mintaelemek alkalmas függvényét (statisztikáját) szeretnénk „közel hozni” az ismeretlen paraméterhez, vagy annak adott függvényéhez.
-t becsüljük). A becsléselmélet alapfeladata, hogy a mintaelemek alkalmas függvényét (statisztikáját) szeretnénk „közel hozni” az ismeretlen paraméterhez, vagy annak adott függvényéhez.
- A fenti fae minta
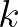 -dimenziós
-dimenziós  , röviden
, röviden 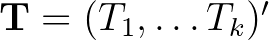 statisztikája torzítatlanul becsli
statisztikája torzítatlanul becsli 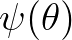 -t, ha
-t, ha
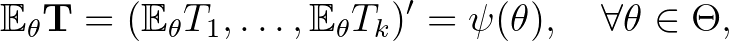
ahol  a transzponálást jelöli (a vektorok oszlopvektorok).
a transzponálást jelöli (a vektorok oszlopvektorok).
- A
 eloszlás szerint az 1-elemű minta
eloszlás szerint az 1-elemű minta  -as Fisher-információs mátrixa:
-as Fisher-információs mátrixa:
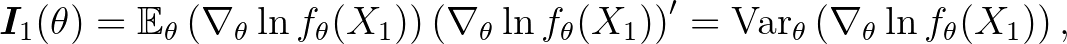
ahol 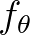 a
a 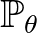 eloszláshoz tartozó sűrűségfüggvény (amennyiben az abszolút folytonos; diszkrét esetben pedig a
eloszláshoz tartozó sűrűségfüggvény (amennyiben az abszolút folytonos; diszkrét esetben pedig a 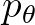 súlyfüggvényt kell használni mindenütt
súlyfüggvényt kell használni mindenütt 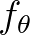 helyett); továbbá
helyett); továbbá 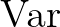 alatt egy véletlen vektor kovariancia-mátrixát értjük. Az utolsó egyenlőség teljesüléséhez fel kell tenni bizonyos regularitási feltételeket (a paraméter szerinti deriválás és a várható érték képzést jelentő
alatt egy véletlen vektor kovariancia-mátrixát értjük. Az utolsó egyenlőség teljesüléséhez fel kell tenni bizonyos regularitási feltételeket (a paraméter szerinti deriválás és a várható érték képzést jelentő 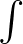 vagy
vagy  felcserélhetők, ami biztosan teljesül, ha a sűrűség- vagy súlyfüggvény tartója nem függ a paramétertől, pl. exponenciális eloszláscsaládban). Ekkor ui.
felcserélhetők, ami biztosan teljesül, ha a sűrűség- vagy súlyfüggvény tartója nem függ a paramétertől, pl. exponenciális eloszláscsaládban). Ekkor ui. 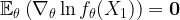 . Ezért a mintaelemek fae volta miatt az
. Ezért a mintaelemek fae volta miatt az 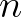 -elemű minta információs mátrixára
-elemű minta információs mátrixára
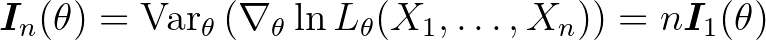
teljesül, ahol 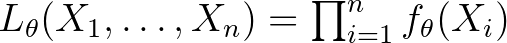 az ún. likelihood-függvény. Érdemes megjegyezni, hogy a Neyman–Fisher-féle faktorizációs tétel miatt
az ún. likelihood-függvény. Érdemes megjegyezni, hogy a Neyman–Fisher-féle faktorizációs tétel miatt 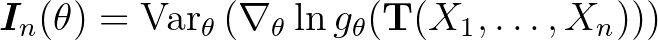 , ahol
, ahol  elégséges statisztika (ismeretében a minta eloszlása már nem függ a paramétertől). Additivitása mellett ez is mutatja a fenti mennyiség információ jellegét és azt, hogy egy elégséges statisztika minden információt magába sűrít a mintából. (Az csak szóhasználat, hogy mintát veszünk, az információs mátrix a konkrét mintavétel nélkül, pusztán egyetlen mintaelem eloszlásából meghatározható, mielőtt megvennénk a mintát.)
elégséges statisztika (ismeretében a minta eloszlása már nem függ a paramétertől). Additivitása mellett ez is mutatja a fenti mennyiség információ jellegét és azt, hogy egy elégséges statisztika minden információt magába sűrít a mintából. (Az csak szóhasználat, hogy mintát veszünk, az információs mátrix a konkrét mintavétel nélkül, pusztán egyetlen mintaelem eloszlásából meghatározható, mielőtt megvennénk a mintát.)
- Ezek után a Cramér–Rao egyenlőtlenség a következő.
1. Tétel. Jelölje 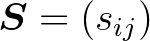 azt a
azt a 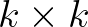 -as mátrixot, amelynek általános eleme
-as mátrixot, amelynek általános eleme 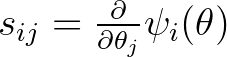 , ahol
, ahol 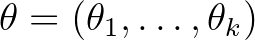 és
és 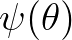 adott differenciálható paraméterfüggvény. Akkor a regularitási feltételek mellett
adott differenciálható paraméterfüggvény. Akkor a regularitási feltételek mellett 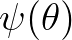 tetszőleges
tetszőleges 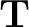 torzítatlan becslésének kovarianciamátrixára (feltéve, hogy az létezik) igaz a
torzítatlan becslésének kovarianciamátrixára (feltéve, hogy az létezik) igaz a
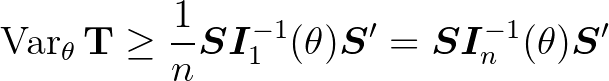
egyenlőtlenség, ami azt jelenti, hogy a bal- és jobboldali mátrix különbsége pozitív szemidefinit.
Megjegyezzük, hogy az információs mátrix 1 valószínűségű pozitív definitását tágabb regularitási feltételek garantálják; ha magát 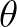 -t becsüljük, akkor
-t becsüljük, akkor 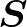 az identitás és az információs (alsó) határ
az identitás és az információs (alsó) határ 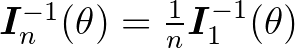 , azaz az ún. hatásos becslés varianciája
, azaz az ún. hatásos becslés varianciája 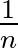 nagyságrendű. (Ha a regularitási feltételek nem teljesülnek, akkor ennek alá tudunk menni nagyságrendileg, pl.
nagyságrendű. (Ha a regularitási feltételek nem teljesülnek, akkor ennek alá tudunk menni nagyságrendileg, pl. ![$[0,\theta ]$](/images/stories/latexuj/2020-09/2020-09-calyampudiradhakrishnarao100eves/img37.png) -n egyenletes eloszláscsalád esetén.) A tételnek számtalan általánosítása létezik, pl. torzított becslésekre.
-n egyenletes eloszláscsalád esetén.) A tételnek számtalan általánosítása létezik, pl. torzított becslésekre.

Cramér és Rao kihirdetik a tételt
A fenti tétel fontos következménye, hogy amennyiben egy torzítatlan becslés kovariancia-mátrixa eléri az információs határt (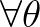 ), akkor biztosan ő a hatásos (torzítatlan becslések közt minimális szórású) becslés a
), akkor biztosan ő a hatásos (torzítatlan becslések közt minimális szórású) becslés a 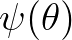 paraméterfüggvényre (ez 1 valószínűséggel egyértelmű). Azonban egyenlőség (a két oldal különbsége a zéró mátrix,
paraméterfüggvényre (ez 1 valószínűséggel egyértelmű). Azonban egyenlőség (a két oldal különbsége a zéró mátrix, 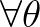 ) nem mindig érhető el. Hatásos becslés azonban ilyenkor is létezhet, amit a következő (Raotól és Blackwelltől származó) tétel garantál (itt nem is kellenek regularitási feltételek).
) nem mindig érhető el. Hatásos becslés azonban ilyenkor is létezhet, amit a következő (Raotól és Blackwelltől származó) tétel garantál (itt nem is kellenek regularitási feltételek).
2. Tétel. Legyen 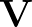 torzítatlan becslés a
torzítatlan becslés a 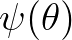 paraméterfüggvényre,
paraméterfüggvényre, 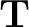 pedig elégséges statisztika (mindketten ugyanattól a fae mintától függenek). Akkor létezik
pedig elégséges statisztika (mindketten ugyanattól a fae mintától függenek). Akkor létezik 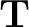 -nek olyan mérhető
-nek olyan mérhető 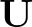 függvénye, mely szintén torzítatlan
függvénye, mely szintén torzítatlan 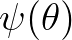 -ra és legalább olyan hatásos, mint
-ra és legalább olyan hatásos, mint 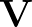 (
( 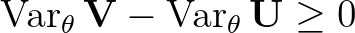 ,
, 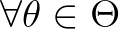 ). A konstrukció:
). A konstrukció: 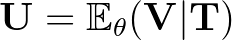 .
.
A fenti konstrukció (Rao–Blackwellizálás) valóban statisztikához vezet, hiszen 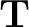 elégséges, így a mellette vett feltételes várható érték nem függ a paramétertől. A tétel bizonyítása egyszerűen következik a feltételes várhatóérték-képzés tulajdonságaiból (Kolmogorov).
elégséges, így a mellette vett feltételes várható érték nem függ a paramétertől. A tétel bizonyítása egyszerűen következik a feltételes várhatóérték-képzés tulajdonságaiból (Kolmogorov).
Az is kijön, hogy amennyiben a 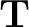 elégséges statisztika teljes is (csak az azonosan 0 függvénye 0 várható értékű,
elégséges statisztika teljes is (csak az azonosan 0 függvénye 0 várható értékű, 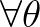 ), akkor a vele való Rao–Blackwellizált 1 valószínűséggel egyértelmű. Ha torzítatlan is, akkor ő a hatásos becslés, ha nem, akkor - amennyiben alkalmas konstanssal (ami függhet
), akkor a vele való Rao–Blackwellizált 1 valószínűséggel egyértelmű. Ha torzítatlan is, akkor ő a hatásos becslés, ha nem, akkor - amennyiben alkalmas konstanssal (ami függhet  -től) való szorzással torzítatlanná tudjuk tenni - megtaláltuk a hatásos becslést. Pl. exponenciális eloszlásnál a
-től) való szorzással torzítatlanná tudjuk tenni - megtaláltuk a hatásos becslést. Pl. exponenciális eloszlásnál a 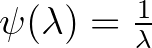 paraméterfüggvényre
paraméterfüggvényre 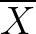 torzítatlan becslés, és mivel elégséges és teljes statisztika is, egyben hatásos becslés is, és varianciája természetesen eléri az információs határt. Viszont magára
torzítatlan becslés, és mivel elégséges és teljes statisztika is, egyben hatásos becslés is, és varianciája természetesen eléri az információs határt. Viszont magára 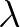 -ra nem érhető el (elvileg sem) a határ. Hatásos becslés azonban létezik:
-ra nem érhető el (elvileg sem) a határ. Hatásos becslés azonban létezik: 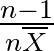 (ha
(ha 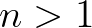 ), ui. ez torzítatlan
), ui. ez torzítatlan 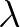 -ra és egyben elégséges, teljes statisztikával valósul meg a becslés.
-ra és egyben elégséges, teljes statisztikával valósul meg a becslés.

Rao és Blackwell kihirdetik a tételt
Utószó
Személyesen először 1991 nyarán találkoztam C. R. Raoval, mikor a Pennsylvania State University statisztika szemináriumára hívtak meg előadást tartani (abban az évben, amelyet a Rutgers Universityn töltöttem). Néhány napig voltam ott, és az első nap reggelén (délben volt az előadásom), amikor bementem az egyetemre, a meghívó kolléga megkérdezte, hogy szeretnék-e C. R. Raóval beszélni, bent van és szívesen fogad az irodájában. Természetesen örültem a lehetőségnek, bár nem számítottam és nem is készültem rá (nem tudtam, hogy akkor ott lesz). Végül is egész délelőtt beszélgettünk. Kérdezte, vannak-e nálam cikkek többváltozós statisztikáról (én gráfklaszterezésből készültem a szemináriumra), és csak két Matematika Intézet preprint volt nálam magyarul (kanonikus korreláció- és korrespondencia-analízis SVD-vel). Ő meglepetésemre gyorsan átnézte és megértette azokat. Örült, hogy SVD módszerekről szóló cikkére hivatkoztam és Rényi maximálkorrelációját is ismerte. Emlékezett Rényire. Mondta, hogy 1973-ban járt Budapesten. Rényi akkor már nem élt (fél évvel Rao után született és fele annyi idő sem adatott meg neki, mint Raonak eddig). Legközelebb az ezredforduló után hívott meg akkor épülő hyderabadi intézetébe, de a cunami és egyéb okok miatt nem tudtam akkor odautazni. Végül 2010-2011 fordulóján jártam az AIMSCS-ben, ahol két előadást tartottam ott és további kettőt Kalkuttában és Bangalore-ban, az ISI ottani központjaiban. Az utolsó napon meghívott vacsorára, ahol feleségével is megismerkedtem. Bhargavi egy ezüst tálkával ajándékozott meg (ma is a polcomon tartom a statisztika könyvek közt) és sajnáltam, hogy nem tudva a találkozásról, én nem vittem neki semmit (gondoltam, majd legközelebb, de sajnos ilyen már nem lesz). Közben Rao írt a Gallery megnyitásáról és a neuronhálózatokról szóló készülő könyvéről (végül is most szeptemberben jelenik meg). Idén májusban felkértek a 100. születésnapjára készülő kötet egy részének lektorálására (híressé vált tanítványai írtak bele és életrajzi cikkek is voltak, részben azokból merítettem). Júniusban ő maga is írt, hogy szívesen találkozna velem születésnapja alkalmából, de a megemlékezés létrejötte még bizonytalan a pandémia miatt. Remélem, hogy stabilnak tűnő egészségét nem ingatja meg a járvány.









