e ötféleképpen

Ugye mindenkinek van kedvenc száma? Az enyém az 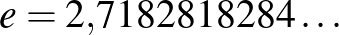$e=2{,}7182818284\dots$ , amellyel legtöbben a középiskolában, a természetes¹ logaritmus alapszámaként találkoznak először. Ez az irracionális (sőt transzcendens) szám minden matematikus közeli barátja, hiszen megannyi helyen bukkan fel. Ebben az írásban öt példát gyűjtöttem össze, a teljesség és a részletes bizonyítások igénye nélkül. Fő célom az Olvasó kíváncsiságának felkeltése.

1. Kártyapakliban

Vegyünk kézbe egy pakli francia kártyát és alaposan keverjük meg. Az 52 lap így kapott sorrendje csupán egyike az összes létező sorrendnek. Vajon azokból mennyi lehet? Ezer? Egy millió? Vagy még annál is több? A válasz, ahogy azt bizonyára az Olvasó is tudja, 52 faktoriális, vagyis

$\displaystyle 52!=52\cdot 51\cdots 2\cdot 1.$

Ez az ártatlannak tűnő szorzat egy felfoghatatlanul nagy számot eredményez. Egészen pontosan

$\displaystyle 80\ 658\ 175\ 170\ 943\ 878\ 571\ 660\ 636\ 856\ 403\ 766\ 975\ 289\ 505\ 440\ 883\ 277\ 824\ 000\ 000\ 000\ 000.$

Gondoljunk bele, ennyi lehetséges kártyakeverés mellett az általunk nyert sorrenddel egyezőt jó eséllyel soha senki nem látott, amióta csak kártyát kevernek²...

Fotó:Jack Hamilton (Unsplash)

Most tekintsük azon sorrendeket, amelyekben egyik kártya sincs az eredeti helyén. Ezekből vajon mennyi lehet? A válasz 52 szubfaktoriális (jelölése $!52$ ), amelynek értéke

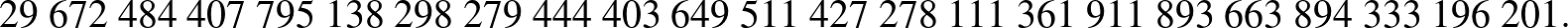
$\displaystyle 29\ 672\ 484\ 407\ 795\ 138\ 298\ 279\ 444\ 403\ 649\ 511\ 427\ 278\ 111\ 361\ 911\ 893\ 663\ 894\ 333\ 196\ 201.$

Az összes sorrendek számát elosztva a „fixpont nélküli” sorrendek számával a következőt kapjuk

$\displaystyle \frac{52!}{!52}=2{,}7182818284\ldots$

A hányados 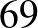$69$ tizedesjegy pontossággal közelíti az 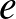$e$ számot! Ez aligha a véletlen eredménye. És valóban, a lapok számának növelésével tetszőlegesen közel juthatunk az 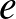$e$ számhoz, amit a matematikusok így fejeznek ki

$\displaystyle e=\lim_{n\to\infty}\frac{n!}{!n}.$

Persze a legfontosabb részletet, a „fixpont nélküli” sorrendek kiszámolását nagyvonalúan kihagytam. A valódi munka itt kezdődik [2].

2. Geometriában

Ha már szóba hoztam a faktoriálist, érdemes megjegyezni, hogy az 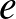$e$ számot sokan a következő összeggel (végtelen sorral) definiálják

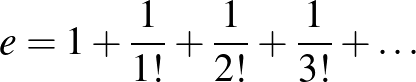
$\displaystyle e=1+\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+\ldots$

Az talán kevésbé köztudott, hogy az összeg minden egyes tagjának geometriai jelentés tulajdonítható.

Tekintsünk ugyanis egy egységnyi hosszúságú szakaszt. A szakaszt egyik végpontja körül forgassuk el 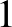$1$ radián szöggel. Ekkor a másik végpont egy 1 hosszúságú körívet rajzol ki. Ezt a körívet kiegyenesítve, a végpont egy 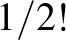$1/2!$ hosszú evolens ívet súrol. Azt kiegyenesítve egy 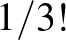$1/3!$ hosszú ív adódik és így tovább. A kiegyenesített ívekből álló törött vonal spirál teljes hossza a fenti végtelen összeg, vagyis $e$ .

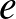A következő videó ennek szemléltetése:

Arra, hogy az ívek hosszai rendre 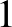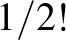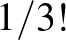$1$ , $1/2!$ , $1/3!$ , ... elemi bizonyítás adható [3].

3. Prímszámokban

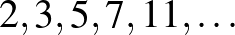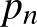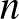A prímszámokat növekvő sorrendbe állítva a $2,3,5,7,11,\dots$ sorozatot kapjuk. Jelölje $p_n$ az $n$ -edik prímet (eszerint pl. 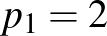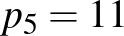$p_1=2$ , $p_5=11$ ). Most szorozzuk össze az első 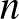$n$ prímet és vonjunk 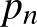$p_n$ -edik gyököt az így kapott szorzatból, vagyis tekintsük az alábbi kifejezést minden 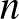$n$ pozitív egészre

$\displaystyle e_n=\sqrt[p_n]{2\cdot 3\cdot 5\cdots p_n}.$

Hogyan viselkedik az így képzett 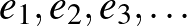$e_1,e_2,e_3,\dots$ sorozat? Az alábbi táblázatban a sorozat néhány tagját gyűjtöttük össze.

$\begin{displaymath}\begin{array}{lcl}e_1&\approx&1{,}4142\\ \hlinee_{10}&\......}7157\\ \hlinee_{1\,000\,000}&\approx&2{,}7172\end{array}\end{displaymath}$

Elképesztő! Habár nagyon lassan, de mintha az 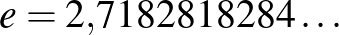$e=2{,}7182818284\dots$ értékhez közeledne a sorozat. Mi köze van a prímszámoknak a természetes logaritmushoz? Erre a választ a számelmélet (azon belül az analitikus számelmélet) egyik legszebb eredménye, a prímszámtétel [4] adja, amely kimondja, hogy az 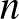$n$ -nél nem nagyobb prímek száma nagy 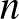$n$ esetén megközelítőleg 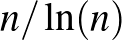$n/\ln(n)$ és minél nagyobb 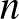$n$ annál pontosabb az egyezés.

4. Hőátadásban

Képzeljünk el kettő ugyanakkora víztartályt, az egyiket a másik fölé helyezve. A felső tartályból 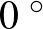$0~^{\circ}$ C-os hideg víz csepeg az alsóban tárolt 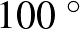$100~^{\circ}$ C-os forróvízbe, amely ugyancsak cseppenként fogy. A folyamat: 1. hideg víz cseppen, 2. hideg csepp elkeveredik, 3. meleg víz cseppen. Tegyük fel, hogy mindkét tartály jól szigetelt (hőt a környezettel nem közöl) és 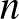$n$ vízcseppet tartalmaz. Hány fokosra hűl le végül az alsó tartály vize? Mennyi a kezdeti ( 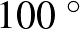$100~^{\circ}$ C) és végső hőmérséklet aránya?

Az alábbi videóban az 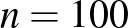$n=100$ esetet láthatjuk.

Lássuk, miként alakul az alsó tartály hőmérséklete cseppenként.

Az 1. vízcsepp után:

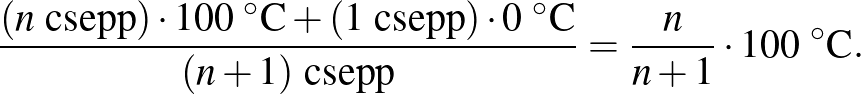
$\displaystyle \frac{(n\text{ csepp})\cdot 100~^{\circ}\text{C}+(1\text{ csepp})... ...circ}\text{C}}{(n+1)\text{ csepp}} = \frac{n}{n+1}\cdot 100~^{\circ}\text{C}.$

A 2. vízcsepp után:

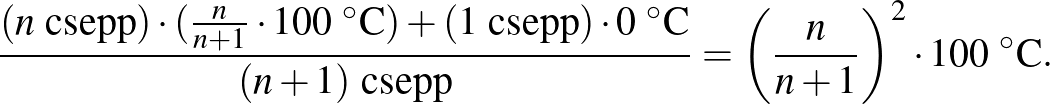
$\displaystyle \frac{(n\text{ csepp})\cdot(\frac{n}{n+1}\cdot 100~^{\circ}\text{... ...(n+1)\text{ csepp}} = \left(\frac{n}{n+1}\right)^2\cdot 100~^{\circ}\text{C}.$

És így tovább egészen az utolsó (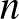 $n$ -edik) vízcseppig

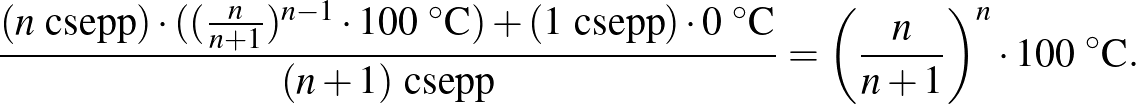
$\displaystyle \frac{(n\text{ csepp})\cdot((\frac{n}{n+1})^{n-1}\cdot 100~^{\cir... ...(n+1)\text{ csepp}} = \left(\frac{n}{n+1}\right)^n\cdot 100~^{\circ}\text{C}.$

Tehát a kezdeti és végső hőmérséklet hányadosa az alsó (meleg vizes) tartályban

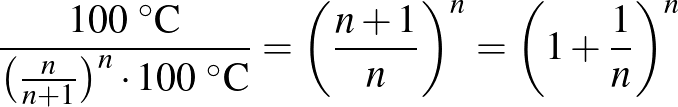
$\displaystyle \frac{100~^{\circ}\text{C}}{\left(\frac{n}{n+1}\right)^n\cdot 100~^{\circ}\text{C}}=\left(\frac{n+1}{n}\right)^n=\left(1+\frac{1}{n}\right)^n$

lesz mire a felső (hideg vizes) tartály kiürül. Ez a hányados egyre nagyobb és nagyobb 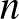$n$ esetén az 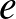$e$ számot tetszőleges pontossággal közelíti, vagyis

$\displaystyle e=\lim_{n\to\infty}\left(1+\frac{1}{n}\right)^n.$

Mellesleg a végső hőmérséklet 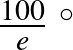$\frac{100}{e}~^{\circ}$ C $\approx 36{,}8~^{\circ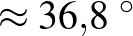}$ C, ami az egészséges testhőmérséklet. Ez persze csak egy véletlen egybeesés.

5. Egy csomag ropiban?

Bontsunk ki egy nagy csomag ropit (sós pálcikát) és kezdjük el a ropikat egyesével véletlenszerűen kettétörni. Ne törekedjünk arra, hogy elfelezzük őket! A lényeg éppen az, hogy egy-egy ropit bármely pontján eltörhetünk és a kettétörések helyei egyenletesen oszlanak el a ropik mentén. A kettétört ropi bal kezünkben maradó darabját helyezzük az asztalra, a másikra nem lesz szükség, megehetjük! Az asztalra helyezett darabokat tegyük egymás után, egy hosszú ropit formálva és amint ez túllépi az 1 ropi hosszt kezdjünk egy új sort. Folytassuk ezt mindaddig, amíg kifogyunk a ropiból! Vajon átlagosan hány darab ropiból fog állni egy-egy sor? Ha másból nem, akkor a cikk címéből és eddigi tartalmából sejthető, hogy a válasz megközelítőleg 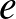$e$ .

Az alábbi videó is ezt mutatja be azzal a különbséggel, hogy kettétört ropik helyett kiégett villanyégőket használunk.

„Na de miért 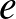$e$ ?”, kérdezhetjük joggal. A magyarázathoz egy kis valószínűségszámításban szerzett tudásra van szükség [5].

Irodalomjegyzék

[1] Kós Rita és Kós Géza, Miért természetes 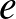?, KöMaL

[2] Hajnal Péter, Kombinatorika előadás, SZTE.

[3] Leo S. Gurin, A Problem, American Mathematical Monthly 103 (1996) 683–686

[4] Prímszámtétel, Wikipédia; https://hu.wikipedia.org/wiki/Pr%C3%ADmsz%C3%A1mt%C3%A9tel

[5] Megoldás (angol nyelven) a math.stackexchange.com oldalon.

Hivatkozások

: ¹ Az érdeklődők joggal kérdezhetik, hogy „Miért természetes 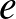?” [1].
: ² A világegyetem kora, nagyjából 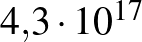$4{,}3\cdot 10^{17}$ másodperc, eltörpül 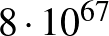$8\cdot 10^{67}$ mellett.