Nemzetközi Matematikai Diákolimpia Rióban

Beszámoló az 58. Nemzetközi Matematikai Diákolimpiáról

Az idei Nemzetközi Matematikai Diákolimpiát 2017. július 12-23. között Brazíliában, Rio de Janeiroban rendezték meg. A versenyen 111 ország 615 diákja vett részt. Ez a résztvevő országok számát és a résztvevő versenyzők számát tekintve is abszolút csúcs. (Az eddigi rekordok 109, ill. 602 voltak.)

A legtöbb ország a megengedett maximális létszámú, 6 fős csapattal szerepelt; az alábbi listában az országnév után zárójelben tüntettem fel az adott ország versenyzőinek számát, ha ez hatnál kevesebb volt.

A résztvevő országok:

Albánia, Algéria, Amerikai Egyesült Államok, Argentína, Ausztrália, Ausztria, Azerbajdzsán, Banglades, Belgium, Beloruszszia, Bolívia, Bosznia-Hercegovina, Botswana, Brazília, Bulgária, Chile, Ciprus, Costa Rica, Csehország, Dánia, Dél-Afrika, Dél-Korea, Ecuador, Egyiptom(3), Elefántcsontpart, Észtország, Finnország, Franciaország, Fülöp-Szigetek, Ghána(1), Görögország, Grúzia, Guatemala(4), Hollandia, Honduras(2), Hong Kong, Horvátország, India, Indonézia, Irak(4), Irán, Írország, Izland, Izrael, Japán, Kambodzsa, Kanada, Kazahsztán, Kenya, Kína, Kirgizisztán, Kolumbia, Koszovo(5), Kuba(1), Lengyelország, Lettország, Liechtenstein(3), Litvánia, Luxemburg, Macedónia, Magyarország, Makaó, Malajzia, Marokkó, Mexikó, Moldova, Mongólia, Montenegro(4), Myanmar, Nagy-Britannia, Németország, Nepál, Nicaragua(4), Nigéria(4), Norvégia, Olaszország, Oroszország, Örményország, Pakisztán, Panama(1), Paraguay, Peru, Portugália, Puerto Rico(5), Románia, El Salvador(4), Spanyolország, Sri Lanka, Svájc, Svédország, Szaúd-Arábia, Szerbia, Szingapúr, Szíria, Szlovákia, Szlovénia, Tadzsikisztán, Tajvan, Tanzánia(2), Thaiföld, Törökország, Trinidad és Tobago(1), Tunézia(5), Türkmenisztán, Uganda, Új-Zéland, Ukrajna, Uruguay, Üzbegisztán(5), Venezuela(5), Vietnam.

A versenyen szokás szerint mindkét napon négy és fél óra alatt 3-3 feladatot kellett megoldani. (A feladatokat alább közöljük.) Mindegyik feladat helyes megoldásáért 7 pont járt, így egy versenyző maximális teljesítménnyel 42 pontot szerezhetett. A verseny befejezése után megállapított ponthatárok szerint aranyérmet a 25-35 pontot elért, ezüstérmet a 19-24 pontos, míg bronzérmet a 16-18 ponttal rendelkező tanulók szereztek. (35-nél több pontot nem szerzett senki.) Dicséretben részesültek azok a versenyzők, akiknek 16-nál kevesebb pontjuk volt, de egy feladatot hibátlanul megoldottak.

A magyar csapatból
Borbényi Márton (Kaposvári Táncsics Mihály Gimn., 12. o. t.) és
Gáspár Attila (Miskolc, Földes Ferenc Gimn., 11. o. t.) egyaránt 25 ponttal aranyérmet,
Williams Kada (Szegedi Radnóti Miklós Kísérleti Gimn., 12. o. t.) 22 ponttal ezüstérmet,
Baran Zsuzsanna (Debreceni Fazekas Mihály Gimn., 12. o. t.) pedig 18 ponttal bronzérmet szerzett.

Kovács Benedek (Budapesti Fazekas Mihály Gyak. Ált. Isk. és Gimn., 12. o. t.) 13 ponttal dicséretben részesült,
Matolcsi Dávid (Budapesti Fazekas Mihály Gyak. Ált. Isk. és Gimn., 10. o. t.) 12 pontot szerzett.

A magyar csapat vezetője Pelikán József (ELTE TTK, Algebra és Számelmélet Tanszék), helyettes vezetője Dobos Sándor (Budapesti Fazekas Mihály Gyak. Ált. Isk. és Gimn.) volt. Kós Géza (MTA SZTAKI, ELTE TTK) a feladatkiválasztó bizottság tagjaként és koordinátorként működött közre az olimpián.

Folyamatban a magyar dolgozatok elbírálása

Az országok (nem-hivatalos) pontversenyében Magyarország a résztvevő 111 ország között a 22-24. helyen végzett. A csapatverseny élmezőnyének sorrendje így alakult (megszerzett pontszámaikkal):

1. Dél-Korea 170, 2. Kína 159, 3. Vietnam 155, 4. USA 148, 5. Irán 142, 6. Japán 134, 7-8. Szingapúr és Thaiföld 131, 9-10. Nagy-Britannia és Tajvan 130, 11. Oroszország 128, 12-13. Görögország és Grúzia 127, 14-16. Belorusszia, Csehország és Ukrajna 122, 17. Fülöp-Szigetek 120, 18-21. Bulgária, Hollandia, Olaszország és Szerbia 116, 22-24. Lengyelország, Magyarország és Románia 115, 25. Kazahsztán 113, 26-28. Argentína, Banglades és Hong Kong 111, 29. Kanada 110, 30. Peru 109, 31. Indonézia 108, 32. Izrael 107, 33. Németország 106, 34. Ausztrália 103, 35-36. Horvátország és Törökország 102, 37-38. Brazília és Malajzia 101, 39-40. Franciaország és Szaúd-Arábia 100 ponttal.

Szeretnék köszönetet mondani a versenyzők tanárainak. Az alábbi felsorolásban minden tanár neve után monogramjukkal jelöltem azokat a diákokat, akik a tanítványaik:

Berzsán Gabriella (BM), Dobos Sándor (BM, BZs, GA, KB, MD, WK), Fazakas Tünde (KB), Gulyás Tibor (GA), Győry Ákos (GA), Juhász Péter (MD), Kiss Gergely (MD), Kiss Géza (MD), Kosztolányi József (WK) Kubatov Antal (BM), Lakatos Tibor (BZs), Mike János (WK), Molnár-Sáska Gábor (KB), Nagy Zoltán Lóránt (BZs), Pósa Lajos (BM, BZs, GA, KB, MD, WK), Schultz János (WK), Szűcs Gábor (GA), Tóth Mariann (BZs).

Ugyancsak szeretnék köszönetet mondani Dobos Sándornak mint a központi olimpiai előkészítő szakkör vezetőjének, továbbá mindazoknak, akik a felkészítésben közreműködtek.

Idén az olimpiai csapat kijelölése válogatóversenyek formájában történt. A válogatóverseny utolsó, kétnapos részét Kecskeméten rendeztük. Szeretnék köszönetet mondani a kecskeméti Mategye Alapítványnak azért, hogy a versenyt nagyvonalúan vendégül látták.

Az idei versenyre is rányomta bélyegét a túl nehéz feladatok kitűzése, ez azonban még a korábbi éveknél is szembetűnőbb volt. A hagyományosan legnehezebb 3. és 6. feladat közül a hatodikat a 615 versenyzőből csak 14 tudta megoldani, a harmadikat pedig csak 2(!) versenyző (egy ausztrál és egy orosz). A korábbi években még a nehéz feladatokra is jónéhányan kaptak töredékpontokat, idén a 3. feladatra a 615 diák közül 608 nulla pontot kapott! Mivel ugyanakkor a könnyűnek szánt (és ezen a szinten tényleg könnyű) 1. ill. 4. feladatra 446 ill. 394 teljes megoldás érkezett, a verseny lényegében a maradék két feladaton dőlt el. Ennek következménye a csapatok közötti holtversenyek (sőt hármas és négyes holtversenyek) abnormálisan magas száma. A kitűzött feladatok nehézségének jó megválasztása a korábbi években is visszatérő téma volt, azonban most nyilvánvalóvá vált, hogy erre a kérdésre a jövő évi olimpián megkülönböztetett figyelmet kell majd fordítani.

A rendezők által szervezett kirándulások közül kiemelkedett az, hogy a résztvevőknek alkalmuk volt meglátogatni a legendás Maracana stadiont.

A következő matematikai diákolimpiát Románia rendezi Kolozsvárott, 2018. július 3-14. között.

Pelikán József

A verseny feladatai:

2017. július 18., kedd

1. Feladat. Minden $a_0 > 1$ egész számra definiáljuk az $a_0$ , $a_1$ , $a_2$ , ... sorozatot a következőképpen. Minden $n\ge 0$ -ra legyen

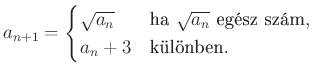
$\displaystyle a_{n+1}=\begin{cases} \sqrt{a_n}&\text{ha } \sqrt{a_n} \text{ egész szám},\\ a_n+3&\text{különben.} \end{cases}$

Határozzuk meg az összes olyan $a_0$ értéket, amihez van olyan $A$ szám, amire $a_n = A$ teljesül végtelen sok $n$ -re.

2. Feladat. Legyen $\mathbb{R}$ a valós számok halmaza. Határozzuk meg az összes olyan $f \colon \mathbb{R} \to \mathbb{R}$ függvényt, amire minden valós $x$ , $y$ szám esetén teljesül

$\displaystyle f \left( f(x) f(y) \right) + f(x+y) = f(xy).$

3. Feladat. Egy vadász és egy láthatatlan nyúl egy játékot játszik az euklideszi síkon. A nyúl $A_0$ kiindulópontja és a vadász $B_0$ kiindulópontja egybeesnek. A játék $(n-1)$ -edik menete után a nyúl az $A_{n-1}$ pontban, a vadász a $B_{n-1}$ pontban van. A játék $n$ -edik menetében a következő három dolog történik, ebben a sorrendben:

(i) A nyúl láthatatlan módon egy olyan $A_n$ pontba megy, amire $A_{n-1}$ és $A_n$ távolsága pontosan 1.

(ii) Egy nyomkövető eszköz megad egy $P_n$ pontot a vadásznak. Az eszköz által a vadásznak nyújtott információ mindössze annyi, hogy $P_n$ és $A_n$ távolsága legfeljebb 1.

(iii) A vadász látható módon egy olyan $B_n$ pontba megy, amire $B_{n-1}$ és $B_n$ távolsága pontosan 1.

Igaz-e, bárhogyan mozogjon is a nyúl, és bármilyen pontokat jelezzen is a nyomkövető eszköz, hogy a vadász mindig meg tudja úgy választani a mozgását, hogy $10^9$ menet után a távolság közte és a nyúl között legfeljebb $100$ legyen?

2017. július 19., szerda

4. Feladat. Legyenek $R$ és $S$ különböző pontok egy $\Omega$ körön, amikre $RS$ nem átmérője a körnek. Legyen $\ell$ az $\Omega$ körhöz a $R$ pontban húzott érintőegyenes. Legyen $T$ az a pont, amire teljesül az, hogy $S$ az $RT$ szakasz felezőpontja. Legyen $J$ egy olyan pont az $\Omega$ kör rövidebb $RS$ ívén, amire teljesül az, hogy a $JST$ háromszög $\Gamma$ körülírt köre az $\ell$ egyenest két különböző pontban metszi. Legyen $\Gamma$ és $\ell$ metszéspontjai közül az $A$ pont az, ami közelebb van az $R$ -hez. Az $AJ$ egyenes $\Omega$ -val vett második metszéspontja legyen $K$ . Bizonyítsuk be, hogy a $KT$ egyenes érintője a $\Gamma$ körnek.

5. Feladat. Adott egy $N \ge 2$ egész szám. $N(N+1)$ futballjátékos, akik között nincs két egyenlő magasságú, valahogyan felállnak egy sorban. Az edző ki akar hagyni ebből a sorból $N(N-1)$ játékost úgy, hogy a megmaradt $2N$ játékos alkotta sor játékosaira teljesüljön az alábbi $N$ feltétel:

(1) senki nem áll a legmagasabb és a második legmagasabb játékos között,

(2) senki nem áll a harmadik legmagasabb és a negyedik legmagasabb játékos között,

$\vdots$

( $N$ ) senki nem áll a két legalacsonyabb játékos között.

Bizonyítsuk be, hogy ez mindig megtehető.

6. Feladat. Egy egész számokból álló $(x,y)$ rendezett párt primitív rácspontnak nevezünk, ha $x$ és $y$ legnagyobb közös osztója 1. Ha adott primitív rácspontok egy véges $S$ halmaza, bizonyítsuk be, hogy van olyan $n$ pozitív egész, és vannak olyan $a_0$ , $a_1$ , ..., $a_n$ egészek, hogy minden $(x,y)$ $S$ -beli pontra teljesül