,,A Kürschák József Matematikai Tanulóversenyt 1894-ben indította a Bolyai János Matematikai Társulat és az Eötvös Loránd Fizikai Társulat közös elődje, a Mathematikai és Physikai Társulat abból a célból, hogy maradandó emléket állítson báró Eötvös Lorándnak, a társulat akkori elnökének vallás- és közoktatásügyi miniszterré történt kinevezése alkalmából. Eleinte 100, ill. 50 koronával járó I. és II. b. Eötvös díjban, ill. dicséretben részesítették a legjobb versenyzőket. A versenyen érettségizett tanulók indulhattak és használhatták a magukkal hozott könyvet és jegyzetet. A kezdetektől egészen a mai napig érvényes, hogy egyetlen fordulóban három feladatra 4 óra munkaidő áll rendelkezésre.
A versenyeket az első világháborúig Budapesten és Kolozsvárott rendezték meg, az 1919 és 1921 közötti három évben érthető okokból nem volt verseny, majd 1922-től Kolozsvár helyett Szeged lett a második helyszín. A második világháború alatt ismét kényszerű szünet következett: 1944 és 1946 között ismételten kimaradt 3 év, de egyúttal az Eötvös Lorándról elnevezett matematikaversenyeknek is vége szakadt. Az alapító jogutódja, a Bolyai János Matematikai Társulat 1947-ben szervezte újra a versenyt, ám azt ekkor Bolyai Jánosról nevezték el. A szabályok pedig annyiban változtak, hogy az érettségi előtt álló tanulóknak is megengedték az indulást. A verseny 1949-ben kapta meg a jelenlegi elnevezését. Az újraindulás után minden évben megrendezték a versenyt valamikor október eleje és november eleje között, az egyetlen kivétel érthetően 1956 volt. (Az 1990-es taxisblokád alatt is megtartották a versenyt: Budapesten gyalog vagy kerékpáron érkeztek a versenyzők az Árpád gimnáziumba.)
A Kürschák verseny sikerének két fontos tényezőjét emeljük ki. A kitűzött feladatok kiválóan megfelelnek a kezdetben megfogalmazott céloknak: a megoldáshoz a középiskolában tanított ismereteken túl nincs szükség további tudásra, hanem sokkal inkább a matematikai gondolkodásmód alkalmazásával lehet elérni a sikert. Íratlan hagyomány, hogy a feladatok megoldásához lehetőleg ne fárasztó számolás, hanem az összefüggések átlátása illetve egy-egy jó ötlet vezessen. Ebben a tekintetben a verseny talán a világon is egyedülálló.
A verseny sikerének másik kulcsa a Kürschák által elindított munka, a Matematikai versenytételek. Ez az a könyv, amiben az 1894 és 1928 közötti versenyek feladatait (tételeit), azok megoldását és a díjazottak neveit találjuk...
A Kürschák versenyen elért díj volt az egyik első sikere számos, később komoly tudományos karriert befutott egykori versenyzőnek. A már nem élők közül a teljesség igénye nélkül az alábbiakat emeljük ki (időrendben): Fejér Lipót, Kármán Tódor Tivadar, Kőnig Dénes, Haar Alfréd, Szegő Gábor, Radó Tibor, Rédei László, Kalmár László, Teller Ede, Bakos Tibor, Gallai Tibor, Szele Tibor, Schweitzer Miklós. Ahogy említettük, a háború után az érettségi előtt álló tanulók is elindulhattak, így ugyanaz a versenyző több díjat is nyerhetett. Az alábbi versenyzők többször is Kürschák díjazottak voltak, nevük után zárójelben az elnyert díjaik száma áll: Szkerka Pál (2), Kálmán Lajos (2), Vigassy József (2), Bollobás Béla (3), Kóta József (2), Máté Attila (2), Gerencsér László (2), Lovász László (2), Bajmóczy Ervin (3), Ruzsa Imre (2), Kollár János (2), Prőhle Péter (2), Tardos Gábor (4), Bohus Géza (2), Magyar Ákos (2), Erdős László (2), Kós Géza (3), Montágh Balázs (2), Sustik Mátyás (2), Kálmán Tamás (2), Burcsi Péter (2), Braun Gábor (2), Lippner Gábor (3), Kun Gábor (2), Terpai Tamás (2), Csikvári Péter (2), Csóka Endre (2), Rátz Béla András (2), Jankó Zsuzsanna (3), Nagy Csaba (2), Korándi Dániel (2), Lovász László Miklós (2), Éles András (2), Nagy János (2), Tomon István (2).”
(Részletek a Bolyai Társulat által 2010-ben kaidott Cserepek a magyarországi tehetséggondozóműhelyekből című kötetből (Kürschák verseny, 28-33.o). A teljes könyv pdf formátumban letölthető a MATEGYE Alapítvání honlapjáról: http://www.mategye.hu/?pid=cserepek .)
A Bolyai János Matematikai Társulat a 2016. évi Kürschák József Matematikai Tanulóversenyt október 7-én, középeurópai idő szerint 14 órai kezdettel rendezte meg a következő huszonhárom helyszínen: Békéscsaba, Bonyhád, Budapest, Cambridge, Csíkszereda, Debrecen, Eger, Győr, Kaposvár, Kecskemét, Kolozsvár, Koronka (Marosvásárhely), Miskolc, Nagykanizsa, Nyíregyháza, Pécs, Sopron, Szeged, Székesfehérvár, Szombathely, Tatabánya, Veszprém és Zalaegerszeg.
A Társulat elnöksége a verseny lebonyolítására az alábbi bizottságot kérte fel: Biró András, Fleiner Tamás (elnök), Frenkel Péter, Kós Géza, Maga Péter, Pach Péter Pál (titkár), Pelikán József. A bizottság szeptember 15-i ülésén a következő feladatokat tűzte ki:
1. Legyenek ![]() egészek. Az
egészek. Az ![]() halmaznak legfeljebb hány
halmaznak legfeljebb hány ![]() elemű részhalmaza adható meg úgy, hogy közülük bármely kettő valamelyike a kettejük uniójának
elemű részhalmaza adható meg úgy, hogy közülük bármely kettő valamelyike a kettejük uniójának ![]() legkisebb eleméből álljon?
legkisebb eleméből álljon?
2. Bizonyítsuk be, hogy pozitív egész számok tetszőleges véges ![]() halmazának van olyan
halmazának van olyan ![]() részhalmaza, amelyre fennáll az alábbi két feltétel.
részhalmaza, amelyre fennáll az alábbi két feltétel.
- • Ha
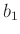 és
és 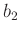 a
a 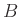 különböző elemei, akkor sem
különböző elemei, akkor sem 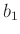 és
és 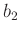 , sem pedig
, sem pedig 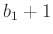 és
és 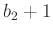 nem egymás többszörösei, továbbá
nem egymás többszörösei, továbbá - • az
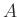 halmaz tetszőleges
halmaz tetszőleges 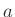 eleméhez van
eleméhez van 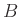 -nek olyan
-nek olyan 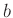 eleme, amelyre
eleme, amelyre 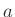 osztója
osztója 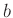 -nek vagy
-nek vagy 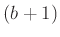 osztója
osztója 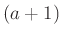 -nek.
-nek.
3. Igaz-e, hogy ha ![]() és
és ![]() olyan valós együtthatós polinomok, melyekre
olyan valós együtthatós polinomok, melyekre ![]() teljesül minden valós
teljesül minden valós ![]() -re, akkor létezik olyan valós együtthatós
-re, akkor létezik olyan valós együtthatós ![]() polinom, amelyre
polinom, amelyre ![]() teljesül minden valós
teljesül minden valós ![]() -re?
-re?
A bizottság a beérkezett dolgozatok átnézése után, november 30-i ülésén a következő jelentést fogadta el:
,,A verseny minden helyszínen rendben zajlott le. Budapesten a megjelent 66-ból 61, míg a további helyszíneken összesen 40 versenyző adott be dolgozatot.
Az idei versenyen a számos versenyző által megoldott első feladat bizonyult a legkönnyebbnek. Ezzel szemben a második feladat esetében kifogástalan megoldás nem érkezett, mindössze öt versenyző ért el jelentős részeredményt. A harmadik feladatot öten oldották meg, és ígéretes próbálkozás is akadt.
Egyetlen versenyző teljesítménye haladta meg lényegesen két feladat megoldását, aki a harmadik feladatra adott elegáns, az algebra alaptételét nélkülöző megoldás mellett megoldotta az első feladatot, valamint a második feladatban jutott a megoldás közelébe. Ezért
I. díjban és 40000 Ft pénzjutalomban részesül
Lajkó Kálmán, a Szegedi Radnóti Miklós Kísérleti Gimnázium 12. osztályos tanulója (tanárai Schultz János, Mike János, Kosztolányi József és Pósa Lajos).
Négy versenyző oldotta meg az első és a harmadik feladatot. Ennek megfelelően
II. díjban és fejenként 25000 Ft pénzjutalomban részesülnek
Bukva Balázs, a Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium 11. osztályos tanulója, (tanárai Hujter Bálint, Gyenes Zoltán, Dobos Sándor és Szűcs Gábor),
Gáspár Attila, a miskolci Földes Ferenc Gimnázium 11. osztályos tanulója, (tanárai Kovács Attiláné és Győry Ákos),
Tóth Viktor, a Kaposvári Táncsics Mihály Gimnázium 12. osztályos tanulója (tanárai Kubatov Antal, Tóthné Berzsán Gabriella és Pósa Lajos) és
Williams Kada, a Szegedi Radnóti Miklós Kísérleti Gimnázium 12. osztályos tanulója (tanárai Schultz János, Mike János, Pósa Lajos és Kosztolányi József).
Két további versenyző akadt, aki az első feladat helyes megoldása mellett a második feladatban is jelentős részeredményt ért el. Ennek megfelelően
Dicséretet és fejenként 5000 Ft pénzjutalmat kapnak
Kovács Benedek, a Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium 12. osztályos tanulója (tanárai Fazakas Tünde és Dobos Sándor) és
Molnár-Sáska Zoltán, a Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium 11. osztályos tanulója (tanárai Hujter Bálint, Gyenes Zoltán, Pósa Lajos és Szűcs Gábor).”
Fleiner Tamás
Megjegyzések:
A Jelentés a 2016. évi Kürschák József Matematikai Tanulóversenyről és a feladatok megoldásai megjelentek a KöMaL folyóirat 2017. februári számában (66-72.o).
A Kürschák versenyek feladatai a versenyvizsga.hu oldalon, illetve a KöMaL archívumában találhatók meg: db.komal.hu/KomalHU