A Héttusa rovatban kitűzött feladatokra bárki küldhet megoldást. Elég a feladat kérdésére a feladatok sorszámát és a feltett kérdésekre a válaszokat megküldeni, indoklást, részletes megoldást nem szükséges írni.
A válaszokat a Ez az e-mail-cím a szpemrobotok elleni védelem alatt áll. Megtekintéséhez engedélyeznie kell a JavaScript használatát. címre várjuk. A beküldési határidő: 2024. április 8.
A verseny nyilvántartása érdekében kérjük, hogy megoldásaikat névvel vagy olyan álnévvel írják alá, amit nyilvánosan közzé tehetünk.
Fordulónként a legjobb megoldók közül néhányan könyvjutalmat kapnak.
Versenyzőinket két kategóriában jutalmazzuk: diák (azaz általános vagy középiskolás), illetve felnőtt. Kérjük, hogy beküldéskor jelezzék, melyik kategóriában indulnak. Ha valaki ezt nem jelzi, őt a felnőttek közé soroljuk.
A 4. forduló után az első négy forduló összesítése alapján az élmezőny (10-20 versenyző) jutalomkönyvet kap.
A határidőt követően a megoldások megjelennek a Facebook-oldalunkon. Az ezután beküldött megoldásokat nem értékeljük a versenyben. Az Érintő következő számában olvashatják a legjobb megoldók nevét és a megjegyzéseket, kiegészítéseket a megoldásokhoz.
Feladatrovatunkhoz örömmel veszünk minden segítő szándékot, várjuk új feladatjavaslataikat, valamelyik feladat szép megoldását, vagy a feladat általánosítását.
A 4. forduló feladatai
22. Igaz-e, hogy tetszőleges 
és 
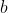pozitív egészekhez van olyan 
pozitív egész szám, amelyre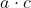 
négyzetszám, 
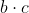köbszám?
23. Hányféle módon lehet szétosztani 17 golyót néhány egymás után sorakozó edénybe úgy, hogy mindegyikbe legalább annyi golyót teszünk, mint amennyi az előző edényekbe összesen került? (Így például 6 golyó szétosztása eszerint a feltétel szerint 6-féleképp történhet: 1-1-4, 1-2-3, 1-5, 2-4, 3-3 és 6.)
24. Zsófi bábukat rak egy üres sakktáblára. Akkor helyezhet el egy bábut egy üres mezőre, ha annak van legalább három üres oldalszomszédja. Legfeljebb hány bábut helyezhet a táblára Zsófi?
25. Az {1,2,3,...,99,100} halmaz legalább kételemű részhalmazát nevezzük átlagosnak, ha a részhalmazban lévő számok átlaga (számtani közepe) egész szám. Az átlagos részhalmazok száma páros vagy páratlan?
26. A síkon felvettünk 11 pontot úgy, hogy nincs közte három olyan, amely egy egyenesre esne, így bármely három pont egy háromszög csúcsait alkotja. Lehetséges-e, hogy a háromszögeknek legalább a fele ugyanakkora területű?
27. Egy kisvárosban 7 buszmegálló van, és néhány autóbuszjárat. Mindegyik buszjáratnak 3 buszmegállója van, és két buszjáratnak legfeljebb egy közös megállója lehet. Legfeljebb hány buszjárat lehet ebben a városban?
28. A hét törpe körbeüli az asztalt, és Hófehérke mindegyiknek annyi cukorkát ad, ahány hüvelyk a különbség a törpe két szomszédjának magassága között. Legfeljebb hány cukorkát oszthat szét közöttük Hófehérke, ha a törpék magassága 31, 32, 33, 34, 35, 36 és 37 hüvelyk?
A feladatokat válogatta: Róka Sándor