Az Érintő Facebook-oldalán már megjelentettük a megoldásokat a rovatszerkesztő, Róka Sándor válogatásában, néhány olyan megoldással és megjegyzéssel, amit a beküldőktől kapott. Ezek újabb általánosításokat, számítógépes megközelítéseket is bemutatnak. Az érdeklődők a KöMaL Fórumában nemrég indított Hétpróba témájába is bekapcsolódhatnak! Szóba kerülhetnek a feladatok, megoldások, félkész ötletek, újabb kérdések: https://www.komal.hu/forum?a=to&tid=365
A Héttusa 2024. júniusi feladatainak megoldásai:
29. Elhelyezhető-e 32 huszár a sakktáblán úgy, hogy mindegyik huszár pontosan két másikat tartson ütés alatt?
A válasz: Igen, elhelyezhető.
Dombi Péter megoldása:
Igen, a sakktábla sarkainál,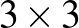 
-as négyzetekben, a középső mező nélkül (bal oldali ábra). Érdekes, hogy hasonlóan csinos alakzat van arra az esetre is, amikor minden huszár pontosan 1 másikat támad (jobb oldali ábra).
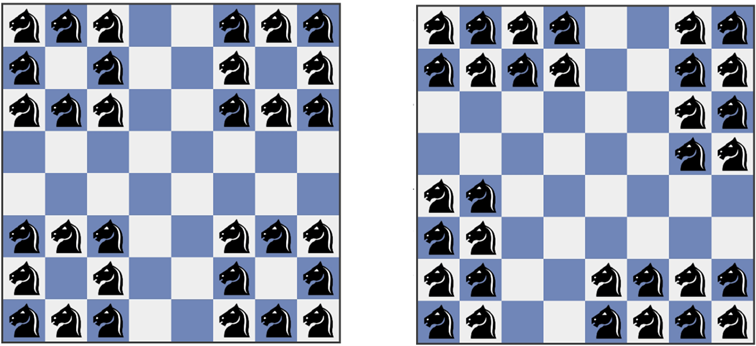
A megoldók többsége a bal oldali ábra szerinti elrendezést találta.
D&2d írja erről: Az segített, hogy a 32 osztható néggyel és a tábla is negyedelhető, ezért ha sikerül 8-at felrakni a negyedére úgy, hogy ne tudjanak „átütni” a másik negyedbe, akkor ez jó lesz.
Makay Géza megoldása:
Programot írtam rá. Mint kiderült, a programom hibás, nem ellenőrzi az összes lehetséges lerakást, de ha átírom úgy, hogy minden lehetséges lerakást ellenőrizzen, akkor záros határidőn belül nem talál megoldást. Ezért úgy hagytam a programomat ebben az értelemben hibásan (mire nem jó, ha az ember hibázik... :) ), és így a program 10 másodperc alatt talált jó néhány érdekes megoldást:
Ebből az első azért érdekes, mert semmilyen szempontból sem szimmetrikus. Ezután jön két eléggé szimmetrikus megoldás. A második sorban levők pedig azt mutatják, hogy a két középső sorban levő 2-2 huszár lehet „kívül” és „belül” is.
Turchányi Gyula is programot írt, ami a feladatnak megfelelő összes megoldást kikeresi, kiszűrve a forgatással fedésbe hozhatók többszörös megjelenítését, de megtartva a tengelyes tükörképeket.
Erről ír a Héttusa feladatok Fórumában a 8. és 9. hozzászólásban.https://www.komal.hu/forum?a=to&tid=365&tc=23
Vukung megadott egy algoritmust: Egy sarokból indulva a lehetséges lépések közül mindig kiválasztok egyet, a többi mezőt pedig „letiltom”, amíg végül vissza nem érek. (Erről küldött egy animációt, ez alább látható.)
30. Lehet-e 8 különböző természetes számot írni egy kocka csúcsaiba úgy, hogy a kocka mindegyik lapja esetén az adott lap csúcsaiban álló négy szám szorzata ugyanaz az érték legyen?
A válasz: Igen, lehet.
Megoldás. A kocka fekete körrel jelölt csúcsaiba írjunk négy különböző prímszámot, és mindegyikkel szemben, az onnan induló testátló másik végére a fehér körbe írjuk ennek a prímszámnak a kétszeresét. Ekkor a kocka minden lapján a csúcsokba írt számok szorzata egyenlő a négy prím szorzatának négyszeresével.
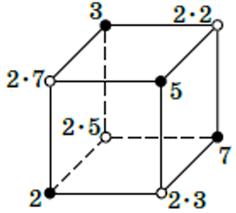
D&2d megoldása: Igen, felírható 8 természetes szám a kocka csúcsaihoz a kívánt módon. Például az „alsó” négy csúcson pozitív körül járás szerint: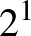 
, 
, 
, 
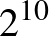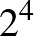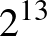, rendre felettük 
, 
, 
, 
.
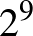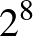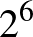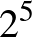Előbb összeggel gondolkodtam: Ha a felső négy csúcshoz pozitív egész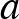 
, 
, 
, 
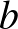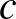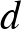-t írok és 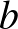alá 
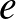-t, akkor a három hiányzó csúcshoz 
, 
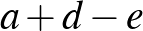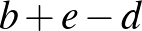és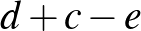 
írandó (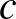, , 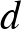ill. 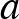alá). Ezt végtelen sok féleképpen tehetjük meg. A hatványozás azonosságai miatt áttérhetünk szorzásra.
Ez a megoldás azt az utat járja, hogy készítünk egy „additív bűvös kockát”, majd a csúcsokban lévő számok helyébe 2-hatványokat írunk, ahol a kitevők az additív kockára írt számok, így kapjuk a multiplikatív bűvös kockát.
Dombi Péter más módszerrel készíti el a kockákat:
Igen, van ilyen számozás a kockán. Additív változatban, az 1-8 számokkal ez egy ismert fejtörő, könnyen megjegyezhető a megoldása is: 1, 8 szomszédos, és mindig a 8 oldalán vannak a Fibonacci-számok :)
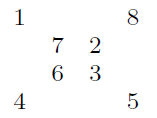
Ezt a megoldást egyszerűen átírhatjuk 2-hatványokkal (vagy bármilyen más alapú hatványokkal) a keresett tulajdonságúra:
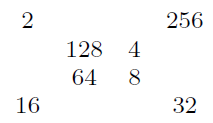
Ha kisebb számokkal is szeretnénk megoldást, akkor kereshetünk más konstrukciót, amivel megoldásokat generálhatunk, ráadásul akár additív, akár multiplikatív tulajdonsággal. Kiindulunk két, nagyon egyszerű számozásból, és ezeket összefűzzük:
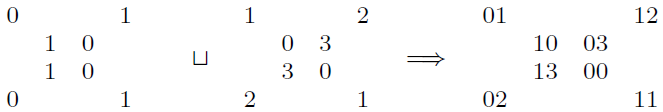
A kétjegyű eredménymátrixot az additív változatban tekinthetjük egy tetszőleges (például 5-ös, vagy akár 10-es) számrendszer kétjegyű számainak:
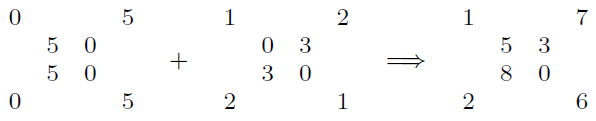
A multiplikatív esetben pedig kitevőknek választjuk két tetszőleges relatív prím számhoz (például 5-höz és 2-höz):
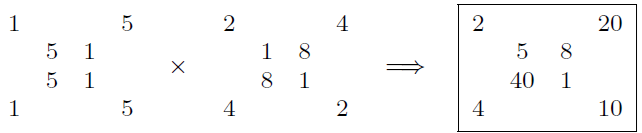
(A megoldás folytatódik, tovább elemzi a problémát, és eljut az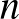 
-dimenziós kockáig.)
31. Egy labdarúgó-bajnokságon legalább 7 csapat indul, és bármely két csapat pontosan egy mérkőzést játszik egymással. Lehetséges-e, hogy a bajnokság győztese a régi pontozási rendszer szerint az utolsó helyen végezne?
A mostani pontozás szerint a mérkőzés győztese 3 pontot, a vesztes 0 pontot kap, döntetlen esetén pedig 1-1 pontot kap a két csapat. A régi rendszer abban különbözik a jelenlegitől, hogy a győzelemért 3 pont helyett 2 pont jár.
A válasz: Igen, lehetséges.
Megoldás. Tegyük fel, hogy 13 csapat vesz részt a bajnokságon, és egyikük, a Csodacsapat 5 mérkőzést megnyert és 7-et elveszített, a többi mérkőzés pedig döntetlennel végződött.
Az új rendszer szerint a Csodacsapat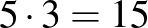 
pontot szerzett. Az általa legyőzött csapatok 1 vereség és 11 döntetlen után 11 pontot gyűjtöttek. Azok a csapatok, akiktől kikapott a Csodacsapat, 
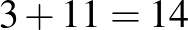pontot szereztek. A jelenlegi pontozás alapján a bajnokság győztese a Csodacsapat.
A régi rendszerben a Csodacsapatnak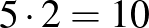 
pontja lenne, míg a többi csapatnak 11, vagy 
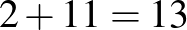. Így számolva a pontokat a bajnokságban a Csodacsapat az utolsó lenne.
Megjegyzés: Változatos indoklások érkeztek, hosszabb elemzések, szép indoklások. Jó lenne, ha ezekről a megoldók írnának a Fórumba.
32. Egy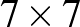 
-es tábla egyik mezőjére leteszünk egy bábut. Újabb bábut akkor tehetünk valamelyik üres mezőre, ha ez a mező legfeljebb egy foglalt mezővel szomszédos. (Két mező akkor szomszédos, ha van közös oldaluk.) Legfeljebb hány bábut tehetünk a táblára?
A válasz: 36.
Megoldás. Figyeljük a mezők oldalait, nevezzük őket falaknak. A 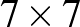-es tábla minden rácsvonala 7 ilyen oldalfalból áll. A 8 függőleges és a 8 vízszintes rácsvonalon összesen 
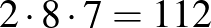oldalfal van.
Számoljuk össze azoknak a falaknak a darabszámát, amelyek legalább egy foglalt mező falát alkotják. Kezdetben egy mező foglalt, ennek 4 fala van. Amikor elfoglalunk egy üres mezőt, akkor az elfoglalt mezők falainak száma legalább 3-mal nő. Ha n bábu áll a táblán, akkor azoknak legalább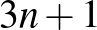 
fala lesz. Az oldalfalak száma legfeljebb 112, azaz 
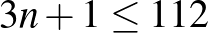, így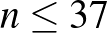 
.
Ha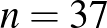 
, akkor 
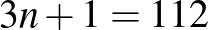, azaz foglalt mind a 112 fal, így a 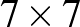-es tábla határán lévő oldalfalak is. Amikor elfoglaljuk az utolsó még szabad faldarabot a tábla határán, akkor az új bábu legalább két másik bábuval lesz szomszédos. Ezt a bábut a feltétel miatt nem tehetjük a táblára. Tehát 
.
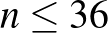Az ábrán látjuk, hogy a táblán állhat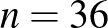 
bábu. A számok a bábuk elhelyezésének sorrendjét mutatják.
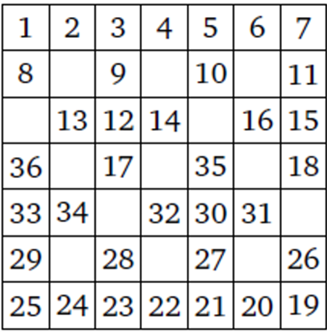
Makay Géza, illetve Udvari Tibor a következő sorrendben helyezte el a bábukat:
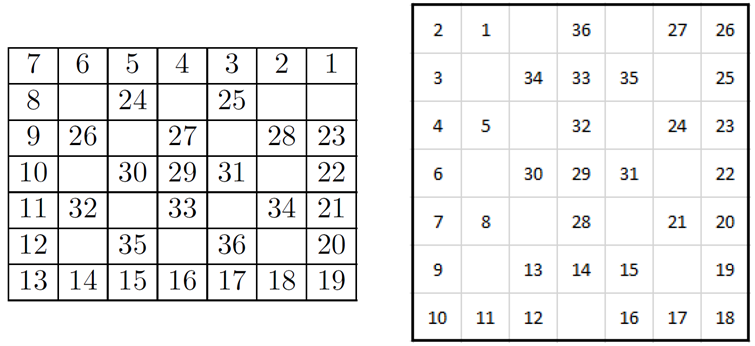
33. Egy 12-oldalú szabályos sokszögnek legfeljebb hány átlóját tudjuk megrajzolni úgy, hogy bármelyik legfeljebb egy másikat metszhet a sokszög belsejében?
A válasz: 14.
Megoldás. Válasszuk ki a sokszög két párhuzamos oldalát, és rajzoljuk meg a velük párhuzamos átlókat. Így a sokszöget trapézokra daraboltuk. Rajzoljuk meg a trapézok átlóit is. Így összesen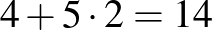 
átlót rajzoltunk, és egyik sem metsz két másik átlót.
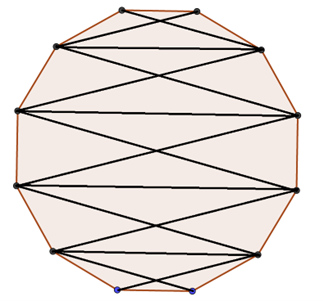
Belátjuk, hogy több átló nem rajzolható meg. Rajzoljunk átlókat a feltételek szerint. Minden metszésponthoz tartozik egy négyszög, amelyben az átlók metszéspontja éppen ez a pont. A metszéspontokhoz tartozó négyszögek között nem lehet átfedés, különben valamelyik átló két másikat is metszene.
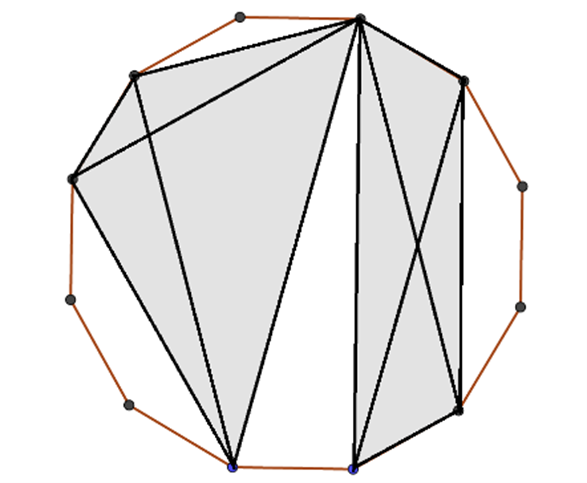
Ezekben a négyszögekben egy-egy átlót elhagyva nem metsző átlókat kapunk, miközben egy-egy négyszögből két háromszög lesz. Egyszerű belátni (pl. teljes indukcióval), hogy egy 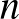-szögben legfeljebb 
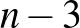nem metsző átlót lehet behúzni, amelyek 
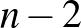háromszögre bontják a sokszöget.
A 12-szög esetén ez 9 átló és 10 háromszög.
Tehát a (legfeljebb) 10 háromszög (legfeljebb) 5 négyszögből keletkezhetett, és mivel négyszögenként egy-egy átlót hagytunk el, ezért a legfeljebb 9 átlóhoz hozzávéve az elhagyott legfeljebb 5 átlót azt kapjuk, hogy az eredetileg behúzott átlók maximális száma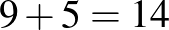 
.
Makay Géza megoldása:
2 átló, amikor metszi egymást, a sokszög belsejét 4 részre bontja. Mivel minden átló legfeljebb egy másikat metszhet a sokszögön belül, ezért bármelyik másik behúzott átló csak valamelyik részen belül mehet (a csúcsokat megengedve). Az első ilyen metszésponthoz négy csúcsot használunk, a részeken belül az újabb metszéspontokhoz mindig legalább két új csúcsot kell használnunk, így maximum 5 metszéspont lehet a sokszög belsejében. Nyilván minél több metszéspontot tudunk létrehozni a sokszög belsejében, annál több átló húzható be, hiszen ha egy átló nem metsz egy másikat, akkor az két részre bontja a sokszöget, és már csak azokon belül lehet átlókat húzni. Az 5 metszéspontot 10 átló produkálja, és ezen kívül csak ezeket nem metsző és (mivel minden csúcs használatban van) ezek határán futó átlók húzhatóak be. Az 5 metszésponthoz tartozó 5 db négyszögnek a 12-szögön belüli (tehát átlós) határa 4 darab lehet, és így maximum 14 átló lehet, arra pedig itt van két példa:
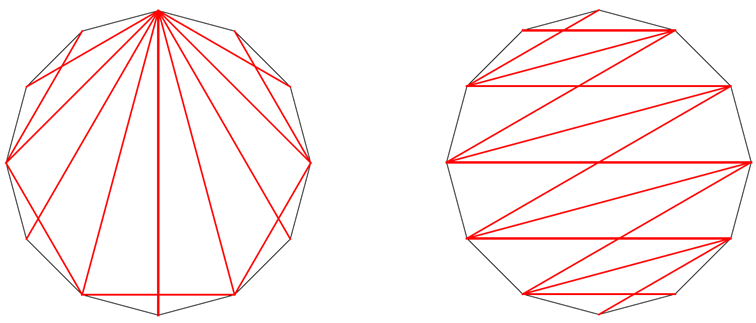
Turchányi Gyula írta: Számítógépes programot írtam a feladatra, szerencsére, mert kézzel csak 13 átlót húztam be, pedig 25 forgatási szimmetriától eltekintő megoldás van, ha a bal és jobbsodrású megoldásokat azonosnak vesszük, még akkor is 16 különböző megoldás van. A program és a rajzok elérhetők a https://github.com/tugyu/erinto33 helyen.
34. Pongrác, a kockafestő művész, egy kocka mindegyik lapját 49 darab egybevágó kis négyzetre osztotta, majd a kis négyzetek mindegyikét befestette pirosra, kékre vagy zöldre úgy, hogy ne legyenek azonos színű szomszédos négyzetek. (Két négyzet szomszédos, ha van közös oldala; és ez a két négyzet lehet a kocka két különböző oldallapján is.) Legkevesebb hány olyan négyzet van, amelyeket Pongrác pirosra festett?
A válasz: 26.
Udvari Tibor megoldása: A kocka minden csúcsánál van három körút (az ábrán szürke, narancs és sárga színnel), amelyek rendre 3, 9 és 15, egymással oldalszomszédos négyzeten mennek át. A páratlan sok négyzet miatt ezeknek az utaknak a mezőit nem lehet két színnel kiszínezni, minden ilyen körútnak tartalmaznia kell mindhárom színt. Tehát mindegyik körút tartalmaz legalább egy piros mezőt. A nyolc csúcshoz összesen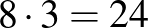 
ilyen körút tartozik, ez legalább 24 piros négyzetet jelent.
A lilával rajzolt körút 21 négyzetes. Ilyenből az egyik testátló két végén levő két csúcshoz tartozóknak nincs közös mezője. Ez alapján még két körút van, amelynek tartalmaznia kell piros mezőt. Összesen ez legalább 26 piros mező.
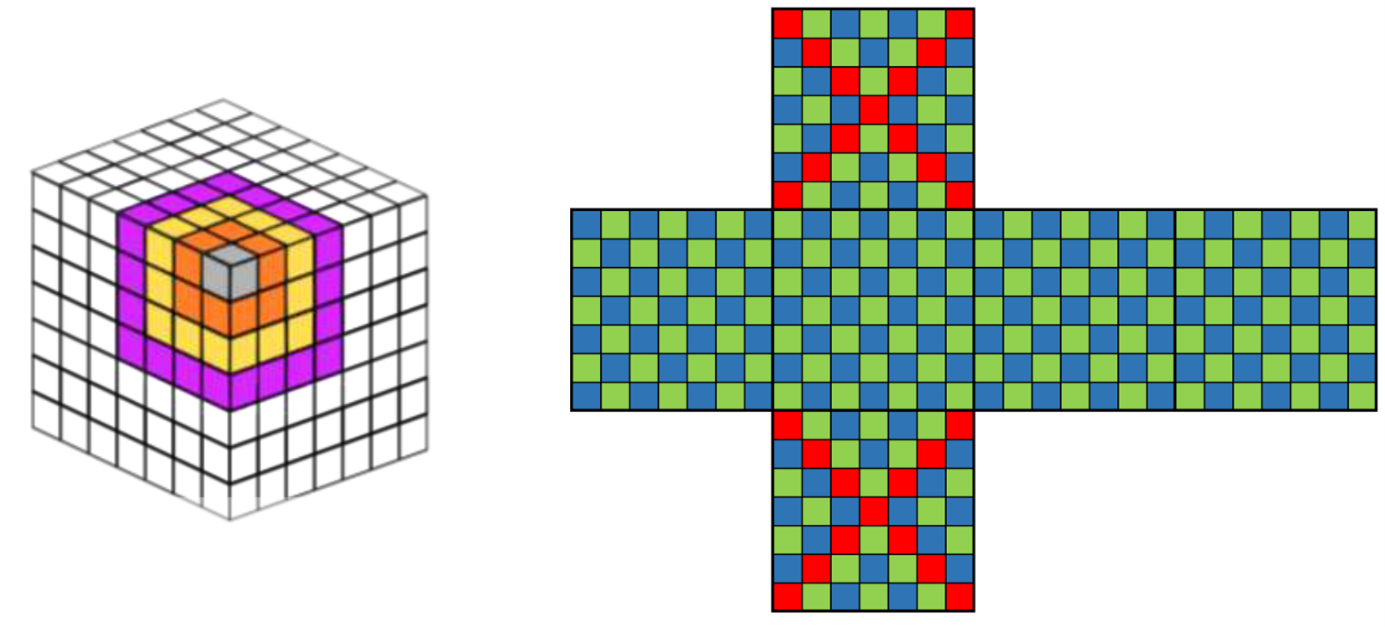
Van is olyan színezés, amely 26 piros négyzetet használ fel. A második ábrán a kiszínezett kocka kiterített hálója látható.
35. Egy távoli szigeten 100 különböző korú bennszülött él. A lakosok egy része igazmondó, a többiek hazugok. Az igazmondók mindig igazat mondanak, a hazugok minden állítása hamis. Egyik nap a száz lakos körbeállt, és mindenki azt mondta, hogy mindkét szomszédja idősebb nála. Következő nap néhányan otthon maradtak, a többiek ismét körbeálltak, és mindegyikük azt mondta, hogy mindkét szomszédja fiatalabb nála. Legkevesebb hány bennszülött maradt otthon ezen a napon?
A válasz: 3.
D&2d megoldása: Legkevesebb három bennszülött maradt otthon.
Az egyszerűség kedvéért legyenek 1, 2, 3, ..., 98, 99, 100 évesek.
Az 1 éves biztosan igazmondó, a 99 éves és a 100 éves biztosan hazudós az első állítások miatt. Ennek a háromnak biztosan otthon kell maradni, különben a második állítással ellentmondásba keverednének. Megmutatom, hogy van olyan ülésrend, amikor elég, ha csak ők hárman maradnak otthon. Üljenek le először 1, 2, 3, ..., 99, 100 sorrendben az asztal köré. Legyen 1 igazmondó, a többi hazudós. Másnap emeljük ki 1, 99, 100-at a körből, a többi ugyanoda üljön, ahová előző nap. Minden rendben az állításokkal.
A megoldásokat átnézte és válogatta: Róka Sándor