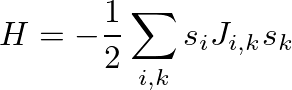Giorgio Parisi 1948-ban született Rómában, kedvező anyagi körülmények között élő polgári családban. Egyetemi tanulmányait 1967–70 között a római La Sapienza Egyetemen végezte, ahol a matematikus és a fizikus szak között ingadozott, végül a fizika mellett döntött, de megtartotta érdeklődését a matematika iránt is.
Az első egyetemi év után felfedezte a Landau–Lifsic elméleti fizikai tankönyvsorozatot, a második év elejére megtanulta az első három kötet anyagát, Dirac kvantummechanikájával együtt. Schrödingert, Fermit és Paulit olvasott, megelőzte az évfolyamot, így nem is igen követte az előadásokat. Minthogy a második egyetemi éve 1968-ra esett, az egyetemi forrongások egyébként is szétzilálták a tanévet.
Az 1968-as év tapasztalatai lényegesen megváltoztatták a családi hagyományoknak megfelelő polgári, liberális kereszténydemokrata beállítódását, nézetei és kapcsolatai erősen balra tolódtak. Társadalmi elköteleződését és aktivitását a mai napig megőrizte.
A harmadik egyetemi évben került kapcsolatba a kutatómunkával. Nicola Cabibbo kevéssel korábban tért vissza Rómába a CERN-ből, az általa képviselt nagyenergiás részecskefizikai témák tűntek a kor vezető tudományos kérdéseinek, és Parisi is ehhez az irányzathoz csatlakozott. Ugyanakkor érdeklődött a statisztikus fizika problémái iránt is, ez a kettőség is végigkísérte pályáját. Értekezését Cabibbo vezetésével írta meg a mértékelméletekben bekövetkező spontán szimmetriasértés és a Higgs-bozon témaköréből. A szabályok által megengedett legrövidebb idő alatt, 1970-ben jutott el a dolgozata megvédéséig.
Első munkahelye a Frascati Nemzeti Laboratórium volt, ahová 1971 elején lépett be ösztöndíjasként. Ez az időszak a Frascati aranykora volt, ekkor kezdték el a világon egyedülálló berendezésen az elektron-pozitron annihilációs kísérleteket.
1981-ben az elméleti fizika professzorává nevezték ki az Universita di Roma II Tor Vergata egyetemen, majd 1992-től az Universita di Roma I La Sapienza egyetem kvantumelméleti professzora lett.
Tudományos cikkeinek a száma meghaladja az ezret, a hivatkozások száma ez idő szerint közel 92 000.
Az idők folyamán nyolc könyvet jelentetett meg a kvantum-kromodinamikától az üvegek elméletéig terjedő témakörben, az utolsó 2022 elején jelent meg In un volo di storni – Le meraviglie dei sistemi complessi (Seregélyek repülése – A komplex rendszerek csodái) címmel.
Tagja számos tudományos akadémiának. Széleskörű szerkesztői és tudományszervezői tevékenységet folytat.
Pályája során számos kitüntetésben részesült, elnyerte egy olasz fizikus által elnyerhető valamennyi nagytekintélyű hazai és nemzetközi díjat, egészen a 2021-es fizikai Wolf-díjig és a Nobel-díjig.

Parisi kutatási területe rendkívül széles: a kvantumtérelmélettől kezdve a részecskefizikán és statisztikus fizikán át kiterjed a húrelméletre, rácstérelméletekre és spinmodellekre, a numerikus módszerek alkalmazására és továbbfejlesztésére, egészen a nagysebességű tömb-processzorokon alapuló dedikált számítógépek tervezéséig, a káosz, dinamikai rendszerek és turbulencia vizsgálatáig, különböző rendezetlen rendszerek (növekedés, véletlen geometriai sokaságok, fehérje folding), de különösen a spinüvegek1, ill. a 90-es évek közepe óta a valódi üvegek tanulmányozásáig, a különféle optimalizációs problémák és algoritmusok kutatásáig, immunológiai problémák és neuronhálók, valamint a gépi tanulás és mesterséges intelligencia kutatásáig, de állatcsoportok kollektív viselkedésének a leírásáig is.
Parisi igen barátságos, könnyen megközelíthető, mindenkit figyelmesen meghallgat. A vele folytatott beszélgetések mindenkit rendkívüli mértékben inspirálnak, mégha sokszor nehéz is az érvelését követni, mert rendkívül gyorsan, óriási ugrásokban gondolkodik. Az évek során igen sok munkatárssal és tanítvánnyal dolgozott együtt, a 70. születésnapjára társszerzőiről készült ábra 317 nevet tartalmaz. Tevékenysége más tudományokban is jelentős előrehaladást indukált, pl. a sztochasztikus folyamatok elméletében, operációkutatásban vagy az algoritmusok elméletében.
Korán felismerte, hogy a számítógépek elterjedése és hatékonyságuk hatalmas megnövekedése a numerikus fizikát a kísérleti és elméleti fizika mellé egyenjogú tudományággá fogja tenni. Ennek a gondolatnak a jegyében kezdeményezte Cabibbo a rácstérelméletek szimulációjára kifejlesztett szuperszámítógép megépítését, amiben Parisi központi tervezői szerepet játszott. Az így létrejött APE nevű 1 gigaflop sebességű tömbprocesszort utóbb 100 gigaflopig terjesztették ki, egy időben számos példány épült belőle és kereskedelmi forgalomba is került.
Ugyancsak ebből a megfontolásból szervezte meg munkatársaival a JANUS együttműködést. A döntően olasz és spanyol kutatók által felépített, fizikailag Zaragozában található dedikált számítógépet kifejezetten a spinüvegek szimulációjára tervezték, és a szimulációk területén egyedülálló módon képes megközelíteni a valódi, laboratóriumi spinüvegminták dinamikáját és karakterisztikus hosszúságskáláit.
Parisi szerteágazó kutatási témái közül kiemelkedik a rendezetlen mágnesek egyik változatának, a spinüvegeknek a vizsgálata, ezért a továbbiakban erre a kérdéskörre fogok fókuszálni. A spinüvegekben az atomi mágnesek (spinek) között versengő, nagyságukra és előjelükre nézve is véletlenszerű kölcsönhatások működnek. Minthogy az ilyen belső konfliktus, az együttműködés és versengés, a serkentés és gátlás a legkülönbözőbb tudományos, műszaki, ökológiai, társadalmi, gazdasági és pénzügyi problémák lényeges eleme, a spinüvegek mindezen komplex rendszerek számára a legegyszerűbb iskolapéldát nyújtják, amelynek jól formalizálható keretei között e komplex rendszerek alapvonásai viszonylag egyszerűen vizsgálhatók.
A spinüveg-metafora rendkívül széles körben bizonyult megtermékenyítőnek, és a spinüvegek elméletében kifejlesztett modellek és módszerek olyan tudományágakba is behatoltak, melyek képviselőinek már sejtelme sincs azokról az eredeti összefüggésekről, amelyek között ezek a módszerek kifejlődtek.
A terület alapmodelljét 1975-ben Edwards és Anderson állították fel. A modell eltekint a tényleges spinüveg atomi szerkezetének leírásától és kizárólag a spinekre fókuszál. A legegyszerűbb esetben ezeket a spineket egy kétértékű változó reprezentálja: 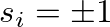 . A spinek között valamilyen adott eloszlásból húzott
. A spinek között valamilyen adott eloszlásból húzott 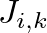 véletlen kölcsönhatások működnek. A modell adott spin-konfigurációjában az energia
véletlen kölcsönhatások működnek. A modell adott spin-konfigurációjában az energia
Ez a standard Ising-modell általánosítása véletlen csatolások esetére. Egyszerűsége dacára máig nem rendelkezünk általánosan elfogadott képpel arról, hogy a modellt pl. a 3-dimenziós rácsra helyezve milyen szerkezetet találunk alacsony hőmérsékleten. A statisztikus fizika szokásos stratégiáját követve Sherrington és Kirkpatrick még ugyanabban az évben, 1975-ben javasolták az Edwards–Anderson-modellnek megfelelő átlagtérmodell bevezetését, ahol is a spinek – feltevés szerint – egy teljes gráfon helyezkednek el, és a 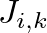 kölcsönhatások minden spinpárt ugyanolyan valószínűséggel kötnek össze pozitív vagy negatív csatolással. Egy ilyen gráf nem helyezhető el véges dimenzióban, ezért gyakran hivatkoznak az átlagtérelméletre végtelen dimenziós modellként.
kölcsönhatások minden spinpárt ugyanolyan valószínűséggel kötnek össze pozitív vagy negatív csatolással. Egy ilyen gráf nem helyezhető el véges dimenzióban, ezért gyakran hivatkoznak az átlagtérelméletre végtelen dimenziós modellként.
Sherrington és Kirkpatrick a modellt az ún. replikatrükk segítségével oldották meg. A replikatrükk színes előtörténete Hardy, Littlewood és Pólya 1934-ben megjelent Inequalities című könyvéig nyomozható vissza, később a polimerek statisztikus fizikájában alkalmazták, elsőként éppen Edwards, így természetes módon talált utat a spinüvegek elméletébe. A replikákra a következők miatt van szükség: Az (1) modellben fellépő véletlen csatolások miatt a rendszer minden makroszkópikus jellemzője (belső energia, szabadenergia, entrópia, mágnesezettség stb.) függeni fog ezektől a véletlen változóktól, így maga is véletlen változó lesz. Azt várjuk azonban (és ezt szigorú matematikai meggondolások is bizonyítják), hogy a nagy részecskeszámok limeszében ezek a makroszkópikus mennyiségek függetlené válnak a véletlen csatolások konkrét realizációjától, „önátlagolnak”. Ezért ahelyett, hogy a különböző termodinamikai mennyiségeket megpróbálnánk a véletlen csatolások függvényében kiértékelni (ami lehetetlen feladat volna), elegendő a termikus átlagolás után kapott mennyiségeket a véletlen csatolások szerint kiátlagolni. A 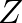 állapotösszeg logaritmusát (ami egyszerűen függ össze a szabadenergiával) kiátlagolva, abból az egész termodinamika meghatározható. Egy véletlen változó logaritmusát azonban nehéz átlagolni, ezért a
állapotösszeg logaritmusát (ami egyszerűen függ össze a szabadenergiával) kiátlagolva, abból az egész termodinamika meghatározható. Egy véletlen változó logaritmusát azonban nehéz átlagolni, ezért a 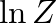 helyett elképzeljük a rendszer
helyett elképzeljük a rendszer 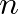 független másolatát (replikáját), ennek az állapotösszege
független másolatát (replikáját), ennek az állapotösszege 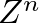 lesz, amelynek az átlagolása könnyebben végrehajtható. Ebből a logaritmus átlaga a
lesz, amelynek az átlagolása könnyebben végrehajtható. Ebből a logaritmus átlaga a
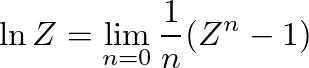
azonosság segítségével kapható meg. Ennek az eljárásnak az a sarkalatos pontja, hogy a replikák számát jelölő 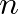 , amely eredeti értelmezése szerint természetes egész, valamiképpen kiterjesztendő a valós számokra, hogy a képletben szereplő limesz elvégezhető legyen. Diszkrét pontokon definiált függvény ilyen kiterjesztése (analitikus folytatása) azonban nem egyértelmű feladat, és további feltételek nélkül nem mindig vezet helyes eredményre.
, amely eredeti értelmezése szerint természetes egész, valamiképpen kiterjesztendő a valós számokra, hogy a képletben szereplő limesz elvégezhető legyen. Diszkrét pontokon definiált függvény ilyen kiterjesztése (analitikus folytatása) azonban nem egyértelmű feladat, és további feltételek nélkül nem mindig vezet helyes eredményre.
Sherrington és Kirkpatrick figyelmen kívül hagyták ezt a nehézséget és végrehajtották a számolást, amelynek során egy ponton a szabadenergia egy 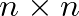 méretű rendparaméter-mátrix
méretű rendparaméter-mátrix 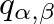 függvényében állt elő. Sherrington és Kirkpatrick ennek a mátrixnak a legtermészetesebb parametrizációját választották, amennyiben feltették, hogy a mátrix invariáns a replikák permutációira. Ezt a választást az a meggondolás motiválta, hogy a replikák segédmennyiségekként kerültek be az egész elméletbe, így semmiféle ok nincs arra, hogy megkülönböztetést tegyünk közöttük. Ezzel a feltevéssel Sherrington és Kirkpatrick olyan formulákhoz jutottak, amelyekben a replikaszámban való analitikus folytatás egyszerűen az
függvényében állt elő. Sherrington és Kirkpatrick ennek a mátrixnak a legtermészetesebb parametrizációját választották, amennyiben feltették, hogy a mátrix invariáns a replikák permutációira. Ezt a választást az a meggondolás motiválta, hogy a replikák segédmennyiségekként kerültek be az egész elméletbe, így semmiféle ok nincs arra, hogy megkülönböztetést tegyünk közöttük. Ezzel a feltevéssel Sherrington és Kirkpatrick olyan formulákhoz jutottak, amelyekben a replikaszámban való analitikus folytatás egyszerűen az 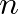 változó valós számmá történő átinterpretálásává vált, és az
változó valós számmá történő átinterpretálásává vált, és az 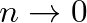 limesz elvégezhető volt.
limesz elvégezhető volt.
Ezzel a replikaszimmetria feltevése elvezetett volna a spinüvegek átlagtér-elméletének a megoldásához. Ennek az eljárásnak a hibája azonnal kiütközött, amikor kiderült, hogy a rendszer entrópiája alacsony hőmérsékleten negatívvá válik, ami egy ilyen diszkrét rendszerben lehetetlen. Pár évvel később de Almeida és Thouless megmutatták, hogy a replikaszimmetrikus megoldás sérti a termodinamikai stabilitás elvét, ezért biztosan elvetendő. Ezzel megindult a replikaszimmetriát sértő megoldások keresése, ami több csoport sikertelen próbálkozása után Parisit 1979-ben elvezette a helyes megoldásig.
Parisi megoldása példátlanul bonyolult volt, és formális, voltaképp nemlétező matematikai fogalmakkal (pl. 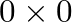 méretű mátrixokkal) operált. A permutációs szimmetria egészen elképesztő, végtelen sokszor iterált koszorúszorzatra való letörését feltételezte, ezzel együtt végtelen sok rendparamétert vezetett be. Parisi elméletét megjelenésekor még a matematikai szigorra kevéssé érzékeny fizikusi körökben is kétely és idegenkedés fogadta. Az eljárás, amely azóta számos tudományágban megjelent, replikaszimmetria-sértés (replica symmetry breaking, RSB) néven terjedt el a rendezetlen rendszerek elméletében.
méretű mátrixokkal) operált. A permutációs szimmetria egészen elképesztő, végtelen sokszor iterált koszorúszorzatra való letörését feltételezte, ezzel együtt végtelen sok rendparamétert vezetett be. Parisi elméletét megjelenésekor még a matematikai szigorra kevéssé érzékeny fizikusi körökben is kétely és idegenkedés fogadta. Az eljárás, amely azóta számos tudományágban megjelent, replikaszimmetria-sértés (replica symmetry breaking, RSB) néven terjedt el a rendezetlen rendszerek elméletében.
A fantasztikusan bonyolult, végtelen sok rendparamétert felvonultató megoldás fizikai jelentésének feltárása több évet váratott magára, míg végül 1983-ban maga Parisi állt elő az elmélet értelmezésével. Kiderült, hogy a spinüveg-átmenet során a fázistér végtelen sok, egymástól makroszkopikus falakkal elválasztott részre (ergodikus komponensre, „völgyre”) bomlik, az elméletben fellépő végtelen sok rendparaméter ezek között a völgyek közti átfedéseket írja le. Az átfedések vizsgálata feltárta a völgyek ultrametrikus geometriáját, a megoldások olyasfajta szerveződését, mint amilyen egy nagy család utolsó generációjának a tagjai között van, ahol az egyedek közti genetikai távolságot a legközelebbi közös ős definiálja. Ennek a képnek pl. az evolúció által létrehozott fajták közti viszonyokhoz való hasonlósága nyilvánvaló, ami lehetővé tette a spinüvegek elméletének a megjelenését egy sor biológiai problémában.
A statisztikus fizika már a születésénél is küzdött az ergodicitás problémájával, vagyis az időbeli átlag és a sokaságra vett átlag közti viszony kérdésével. A fázisátalakulások során a rendszer szimmetriája sérül, bekövetkezik a fázistér felhasadása ergodikus komponensekre. A múlt század hatvanas éveiben a szokásos fázisátmenetek körében sikerült ezt a kérdést rendezni, de voltaképpen bámulatos, hogy az ergodicitás sérülését egyáltalán sikerült beépíteni a statisztikus fizikába. A rendezetlen rendszerek elméletében, speciálisan a spinüvegekben kialakuló ergodicitás-sértés minden korábbinál súlyosabb kihívást jelentett a statisztikus fizika számára, amellyel Parisi heurisztikus megoldását szigorú matematikai alapokra helyezve Michel Talagrand birkózott meg, aki ehhez kidolgozta a sztochasztikus folyamatok elméletének egy egészen új fejezetét, amihez a motivációt Parisi megoldása adta.
Eddig a pontig azt látjuk, hogy ezeknek a furcsa ötvözeteknek, a spinüvegeknek a vizsgálata ugyan hatalmas elméleti fejlődést indukált, de gyakorlati alkalmazásokat nem mutatott fel. Ez a helyzet változott meg 1982-83-ban a bonyolult kombinatorikai optimalizációs problémák, ill. az asszociatív memória modellek és a spinüvegek közti kapcsolat felismerésével. Ez óriási lökést adott a mesterséges neuronhálók elméletének, hatékony optimalizációs algoritmusok bevezetését inspirálta, és széleskörű kapcsolatokat teremtett a statisztikus fizika és a számítógép-tudomány között. A statisztikus inferencia, adatbányászat, gépi tanulás és mesterséges intelligencia kutatásának területén mindenütt felbukkannak a spinüvegek elméletében kidolgozott fogalmak és módszerek. A spinüvegek elméletéből indultak ki az ökonofizika és szociofizika néven ismertté vált új tudományágak is, amelyek a társadalom és a gazdaság különböző folyamatait elemzik statisztikus fizikai módszerekkel. Egy közvetlenül semmiféle gyakorlati hasznot nem hajtó anyagcsalád vizsgálata tehát végeredményben sokezer milliárd dolláros iparágakban használt alkalmazásokhoz vezetett el. Ennek a történetnek megszívlelendő tanulságai vannak a tudományfinanszírozás számára.
Hogy valamennyire érzékeltetni tudjuk a spinüveg-gondolatok fizikán kívüli alkalmazását, adjunk az (1) képletben fellépő mennyiségeknek egészen más jelentést. Gondoljunk el egy vállalatot, amelynek 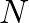 alkalmazottja van, akiket két részleg között kell a vállalatvezetésnek elosztania. Az
alkalmazottja van, akiket két részleg között kell a vállalatvezetésnek elosztania. Az 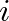 munkatársnak adjunk egy
munkatársnak adjunk egy 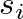 címkét, amely
címkét, amely 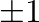 értéket vesz fel annak megfelelően, hogy
értéket vesz fel annak megfelelően, hogy 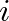 -t az egyik vagy másik részlegbe osztják be. Az alkalmazottak között azonban intenzív érzelmi kapcsolatok vannak, amelyeket a
-t az egyik vagy másik részlegbe osztják be. Az alkalmazottak között azonban intenzív érzelmi kapcsolatok vannak, amelyeket a 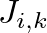 csatolások írnak le;
csatolások írnak le; 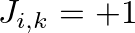 , ha
, ha 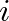 és
és 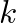 barátok, és −1, ha ellenségek. A vezetés érthető módon arra törekszik, hogy lehetőleg egymással baráti viszonyban álló munkatársak kerüljenek ugyanabba a részlegbe, és az ellenségek lehetőség szerint különböző részlegbe kerüljenek. A dolgot az teszi nehézzé, hogy előfordulhat, hogy három munkatárs kölcsönösen ellenséges viszonyban van, vagy az, hogy egy adott munkatársnak van két olyan barátja, akik egymás ellenségei. Az ilyen frusztrált helyzeteket nem lehet mindenkit kielégítő módon kezelni. A vezetés legfeljebb arra törekedhet, hogy a dolgozókat az itt társadalmi feszültségként interpretált
barátok, és −1, ha ellenségek. A vezetés érthető módon arra törekszik, hogy lehetőleg egymással baráti viszonyban álló munkatársak kerüljenek ugyanabba a részlegbe, és az ellenségek lehetőség szerint különböző részlegbe kerüljenek. A dolgot az teszi nehézzé, hogy előfordulhat, hogy három munkatárs kölcsönösen ellenséges viszonyban van, vagy az, hogy egy adott munkatársnak van két olyan barátja, akik egymás ellenségei. Az ilyen frusztrált helyzeteket nem lehet mindenkit kielégítő módon kezelni. A vezetés legfeljebb arra törekedhet, hogy a dolgozókat az itt társadalmi feszültségként interpretált  energiafüggvény minimumának megfelelő módon ossza el. Ha most feltételezzük, hogy a munkatársak között ugyanakkora valószínűséggel van baráti, mint ellenséges viszony, kiderül, hogy a
energiafüggvény minimumának megfelelő módon ossza el. Ha most feltételezzük, hogy a munkatársak között ugyanakkora valószínűséggel van baráti, mint ellenséges viszony, kiderül, hogy a  minimumának a megkeresése rendkívül nehéz feladat, amelynek a megoldásához szükséges erőforrásigény (pl. számítógépidő) a dolgozók számával exponenciálisan emelkedik. Ráadásul a feladatnak megint csak exponenciálisan sok közel egyenértékű megoldása van, amelyek közül bármelyiket is választjuk, a dolgozók jelentős része boldogtalan lesz. Ha tiltakozásuk hatására a vezetés egy másik optimumot keres, az ugyanannyi munkatárs érdekeit fogja sérteni, legfeljebb másokét, mint az előbbi megoldásban.
minimumának a megkeresése rendkívül nehéz feladat, amelynek a megoldásához szükséges erőforrásigény (pl. számítógépidő) a dolgozók számával exponenciálisan emelkedik. Ráadásul a feladatnak megint csak exponenciálisan sok közel egyenértékű megoldása van, amelyek közül bármelyiket is választjuk, a dolgozók jelentős része boldogtalan lesz. Ha tiltakozásuk hatására a vezetés egy másik optimumot keres, az ugyanannyi munkatárs érdekeit fogja sérteni, legfeljebb másokét, mint az előbbi megoldásban.
Ha a különböző megoldások közti távolságot azzal jellemezzük, hogy hány munkatárs besorolását kell megváltoztatnunk, hogy az egyik optimumból a másikba jussunk, kiderül, hogy a megoldások egy családfa geometriáját mutatják: lesznek közeli optimumok, kissé távolabbiak, még távolabbiak, stb., de soha nem fordul elő, hogy három különböző optimum között három különböző távolságot találjunk, mint ahogy az sem fordul elő, hogy ha valakinek van egy testvére és egy unokatestvére, akkor a testvérnek az unokatestvér másodunokatestvére legyen. Az ilyen metrikával bíró tereket ultrametrikus térnek hívjuk, és a fentiek szerint a  függvény optimumai ultrametrikus geometriát mutatnak.
függvény optimumai ultrametrikus geometriát mutatnak.
Vegyük észre, hogy bár a különböző élőlények közötti genetikai távolságoknak durván ugyanilyen ultrametrikus a szerkezete, ott a „családfákat” a természetes szelekció dinamikája hozza létre. Elgondolkoztató, hogy egy teljesen véletlen szerkezetű problémában ez a szerveződés mindenféle tervezés, vagy kiválasztás nélkül megjelenik: az optimális megoldásoknak ez a szerkezete a nagy számok határesetében spontán épül fel. Parisinek ezt a felismerését, és a modell egzakt megoldásának a megtalálását a Svéd Tudományos Akadémia Nobel-bizottsága a díj odaítélésének egyik döntő indokaként jelölte meg.
Amikor olyan valóságos komplex rendszereket tekintünk, mint amilyen egy élő sejt, az agy, vagy a társadalom, mindig azt látjuk, hogy ezekben a rendszerekben nagyszámú elem (fehérje, idegsejt, ill. a társadalmat alkotó szereplők) között állandó versengés és együttműködés van. Az ilyen rendszerek soha nincsenek egyensúlyban, ehelyett egy többé-kevésbé jól meghatározott munkapont körül ingadoznak, fluktuálnak. Ez az állapotuk hajlékony, a lehetséges optimális állapotok közötti átmenetek révén képesek a környezet változásaihoz alkalmazkodni anélkül, hogy elvesztenék önazonosságukat. Előfordulhat azonban, hogy az együttműködés és versengés, serkentés és gátlás, a fékek és ellensúlyok finom rendszere megsérül, az (1) képletben a csatolások eloszlása túlnyomó többségében pozitívvá válik, ami a sejt esetében rákhoz, az idegrendszerében őrülethez, a társadalom esetében diktatúrához vezet. Ezen a ponton a rendszer komplexitása lehanyatlik, működése súlyosan sérül, vagy egyenesen megszűnik. A komplexitás elvesztése veszélyes. A társadalmi és politikai folyamatok elemzésében a spinüveg-analógia megerősíti Jacob Burkhardt figyelmeztetését: A komplexitás tagadása a zsarnokság lényege.
Kondor Imre
az ELTE Fizikai Intézete nyugalmazott egyetemi tanára
 Ez az írás a Fizikai Szemle 2021/11. számának 365–368.oldalain megjelent cikk némileg rövidített változata, a szerző és a folyóirat szíves engedélyével közöljük.
Ez az írás a Fizikai Szemle 2021/11. számának 365–368.oldalain megjelent cikk némileg rövidített változata, a szerző és a folyóirat szíves engedélyével közöljük.
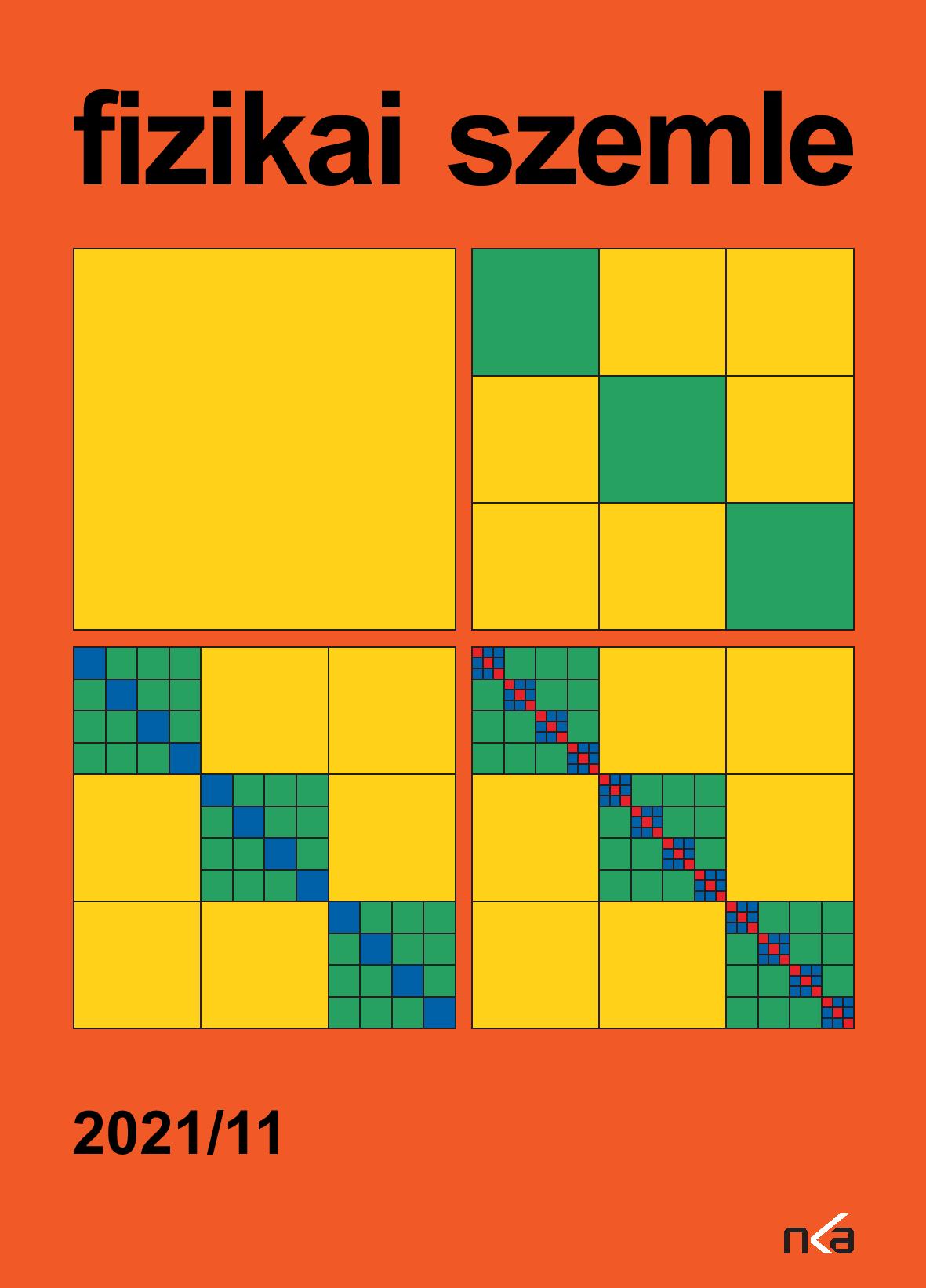
A címlapon a replikaszimmetria-sértés Parisi-féle szerkesztésének első lépései: az ábra a rendparaméter-mátrix szerkezetét kívánja érzé keltetni, azonos színű mezők azonos mátrixelemeknek felelnek meg.
Lábjegyzet
- 1 A spinüvegek olyan mágneses ötvözetek, amelyekben a mágneses atomok spinje alacsony hőmérsékleten látszólag rendezetlen irányokban áll be. Nevükben az „üveg” arra utal, hogy ez az irány szerinti rendezetlenség modellje lehet például az ablaküvegben az atomok elhelyezkedés szerinti rendezetlenségének.