Modellezés Wolfram Mathematica segítségével

Nagy sikerrel zajlott 2021. november 11–12-én a Szegedi Tudományegyetem Bolyai Intézete, a SciExperts kft. és a Wolfram Research Ltd. által szervezett bevezető online Mathematica tréning. Az oktató Dr. Karsai János (Certified Mathematica Trainer), a Bolyai Intézet docense volt.

A tréning folytatása a korábbi hazai és külföldi sikeres intenzív iskoláknak, amelyet a tervek szerint újabb hazai kurzusok, iskolák követnek. A tréningen több mint 50-en vettek részt, egyetemi oktatók, hallgatók, doktoranduszok, ipari alkalmazók, fiatalok és tapasztalt szakemberek egyaránt. Az első 10 jelentkező-résztvevő a tréning után Mathematica ajándékot kapott.

A „zöldmezős” bevezető online képzés során a teljesen kezdő résztvevők is – kiindulva az üres képernyőről, a különböző tudományterületeken felmerülő elemi modellezési problémákon keresztül – megtanulták a Mathematica és a Wolfram Language legfontosabb eszközeit, alkalmazási lehetőségeit (ábrázolások, számítások, dinamikus műveletek, egyszerű programozási technikák). Ugyanakkor a már tapasztaltabb felhasználók is megismerhettek szép új eszközöket. A tréninget követően minden résztvevő képes önállóan egyszerű alkalmazásokat készíteni, használni. A résztvevők átfogó segédanyag-gyűjteményt is kaptak.

A teljesség igénye nélkül tekintsünk meg néhány, a kurzuson elkészült alkalmazást:

Természetesen az ábrázolások, és a szabad szöveges utasítások segítségével tanultuk meg az alapvető szintaktikát:

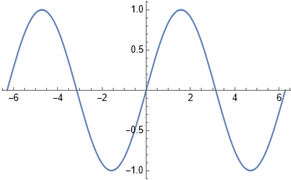
Egy változás vizsgálatában alapvető a változás sebességének a dinamikus vizsgálata:

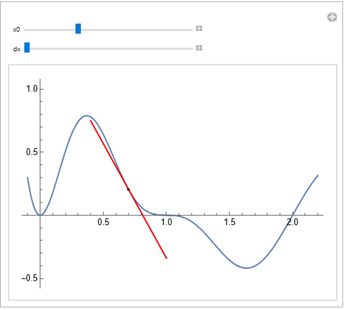
A stroboszkópikus ábra is alapvető eszköz a változások vizsgálatában:

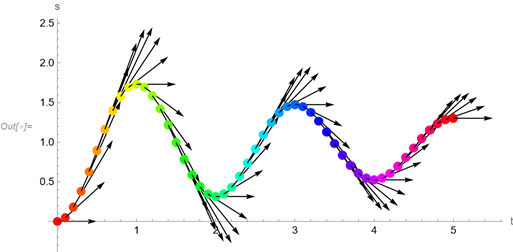
A változás–sebesség elemzése után már csak egy ugrás a véletlen bolyongás:

A többváltozós függvények vizsgálata sem maradhat ki egy bevezető kurzusból. Az ábra egy kétváltozós függvény szintvonalas ábráját, a parciális deriváltak zéró szintvonalait (metszéspontok a kritikus helyek), valamint a legmeredekebb (gradiens) irány szerinti folyamot tartalmazza. A szintvonalak mentén nem változik a függvény, A gradiens irányt követő vonalak mentén tudunk leggyorsabban eljutni a hegycsúcsokra, és ezek merőlegesek a függvény szintvonalaira.

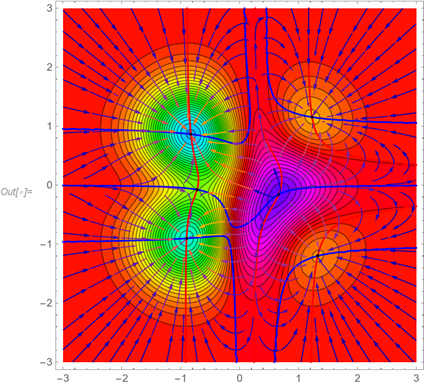
A numerikus algoritmusok, diszkrét folyamatok alapeszköze az iteráció. A mértani sorozat, a Fibonacci-számok és más egyszerű példák után eljutottunk a Newton-iterációig, sőt a kezdeti értékektől érzékeny függést jól szemléltető Newton-fraktálokig és az egyszerű fraktálalakzatok (fák, Koch-görbe, Sierpinsky-háromszög) generálásáig.

Itt a 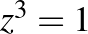egyenlet gyökeit és a hozzá tartozó Newton-fraktált láthatjuk (minden pontot aszerint színezünk, hogy a Newton-iteráció melyik gyökhöz konvergál).

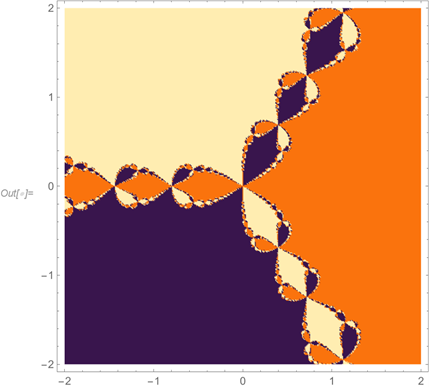
Így készül egy fenyőfa:

Ez pedig az eredmény:

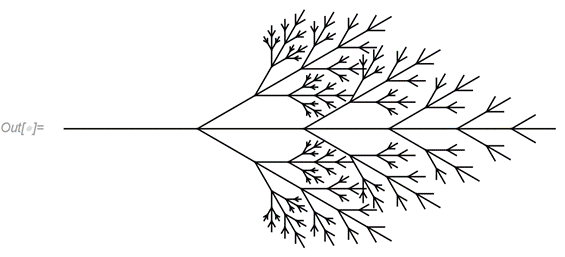
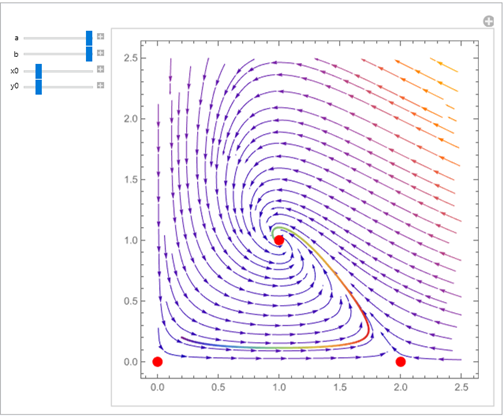
A folytonos differenciálegyenletekkel leírható modellek vizsgálatának alapeszközeit egy ragadozó–áldozat modellen mutattuk be. Az ábrán az

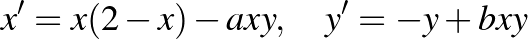
rendszer egyensúlyi helyzetei és trajektóriái láthatók.

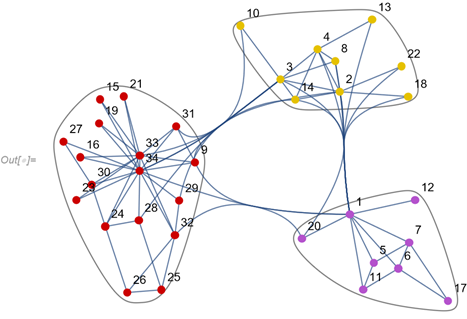
A gráfok vizsgálatának lehetőségeinek bemutatásával zártuk a két aktív napot: Az ábra az elhíresült Zachary karate klub klikkesedését szemlélteti.

Befejezésül, idézzük néhány résztvevő véleményét:

„Kifejezetten tetszett a kurzusban, hogy az előadással párhuzamosan lehetett gyakorlatot szerezni a programkód megírásában, ami nagyban segítette a programnyelv elsajátítását.”

„Nagyon tárgyilagos és hasznos továbbképzés (inkább a komolyan elmélyülni szándékozóknak...).”

„Még egyszer köszönöm a jó hangulatú tréninget, és a jól előkészített segédanyagokat.”