Bevezetés
A már több mint egy éve tartó COVID-19 járvány és különösen az ezzel kapcsolatban naponta frissülő adatsorok a hétköznapi emberek figyelmét is ráirányították a járványmodellezés jelentőségére, holott ez a tudományterület sok évtizedes hagyománnyal és jól bejáratott modellezési megközelítésekkel rendelkezik. Nem kétséges azonban, hogy az újonnan kidolgozott vagy eddig döntően más területeken alkalmazott számítási módszerek további lendületet adnak a témakör fejlődésének így hozzájárulva egy esetleges jövőbeli veszélyhelyzet hatékonyabb kezeléséhez.
Populációs szintű kompartmentális járványmodellek
A tágabban értelmezett kompartmentális modellek fő jellemzője, hogy objektumok (pl. részecskék, anyagok, járművek) vagy élőlények különböző tárolóhelyek (kompartmentek) közti eloszlásának időbeli változását írják le [5]. A kompartmentek lehetnek fizikailag elkülönülő helyszínek (pl. egymással összekapcsolt berendezések, szervek, élőhelyek), de jelölhetnek különböző diszjunkt állapotokat is, mint a járványmodellek esetén látni fogjuk. Mivel a kompartmentális modellek természetes állapotváltozói az egyes kompartmentekhez tartozó anyagmennyiségek, egyedszámok (vagy arányok, koncentrációk), ezért ezek a modellek rendszerint az ún. nemnegatív rendszerek osztályához tartoznak, amelynek fő jellemzője, hogy az állapottér nemnegatív térszeglete invariáns a dinamikára nézve. A nemnegatív modellek egy rendkívül érdekes és hasznos részhalmaza az eredetileg fizikai kémiából származó, de ahhoz képest már lényegesen általánosított kinetikus rendszerosztály, ahol a nemlineáris dinamika formálisan kémiai reakciókkal (azaz reakciógráffal és a hozzá tartozó megfelelő paraméterekkel) realizálható [3].
Tekintsünk egy „kémiai reakciók” formájában megadott egyszerű fertőzési és gyógyulási mechanizmust:



ahol 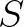 jelöli a fertőzésre fogékony személyeket (susceptible),
jelöli a fertőzésre fogékony személyeket (susceptible), 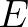 a nemrég megfertőzött, de még nem fertőzőképeseket (exposed),
a nemrég megfertőzött, de még nem fertőzőképeseket (exposed), 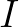 a fertőzőképes fertőzőket (infected) és
a fertőzőképes fertőzőket (infected) és 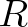 a gyógyultakat (recovered). Az első reakció írja le a fertőzés folyamatát (egy fogékony és egy fertőzött kontaktusa során a fogékony átkerülhet a frissen fertőzött
a gyógyultakat (recovered). Az első reakció írja le a fertőzés folyamatát (egy fogékony és egy fertőzött kontaktusa során a fogékony átkerülhet a frissen fertőzött 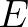 kompartmentbe), a második reakció a fertőzőképesség kialakulását, a harmadik pedig a gyógyulást. Az ún. tömeghatás kinetikát feltételezve a fenti reakciókból könnyen adódnak a jól ismert SEIR járványmodell differenciálegyenletei [2]:
kompartmentbe), a második reakció a fertőzőképesség kialakulását, a harmadik pedig a gyógyulást. Az ún. tömeghatás kinetikát feltételezve a fenti reakciókból könnyen adódnak a jól ismert SEIR járványmodell differenciálegyenletei [2]:
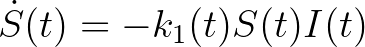
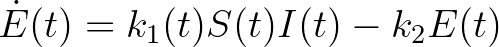
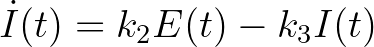
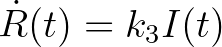
ahol 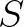 ,
, 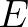 ,
, 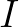 és
és 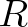 időfüggvények a megfelelő kompartmentek létszámának teljes népességen belüli arányát jelölik,
időfüggvények a megfelelő kompartmentek létszámának teljes népességen belüli arányát jelölik, 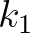 ,
, 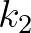 és
és 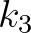 pedig a három reakció reakciósebességi együtthatói:
pedig a három reakció reakciósebességi együtthatói: 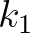 a kontaktusokhoz tartozó fertőzési valószínűséggel arányos (és emiatt a körülmények függvényében időben változó),
a kontaktusokhoz tartozó fertőzési valószínűséggel arányos (és emiatt a körülmények függvényében időben változó), 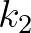 és
és 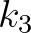 pedig időállandók. Fontos megjegyezni, hogy a modell kinetikus interpretációja a reakcióhálózatok elméletéhez tartozó eredmények [4] alkalmazása mellett jó alapot teremt arra is, hogy a determinisztikus és sztochasztikus (pl. ágens alapú) szimulációkat elméletileg jól megalapozottan összevethessük egymással [6,10].
pedig időállandók. Fontos megjegyezni, hogy a modell kinetikus interpretációja a reakcióhálózatok elméletéhez tartozó eredmények [4] alkalmazása mellett jó alapot teremt arra is, hogy a determinisztikus és sztochasztikus (pl. ágens alapú) szimulációkat elméletileg jól megalapozottan összevethessük egymással [6,10].
Járványmodellek rendszerelméleti keretben
A rendszerelméletben a dinamikus modelleket input-output operátorként fogjuk fel, amelyek manipulálható vagy éppen zavaró bemenetek és megfigyelhető kimenetek kapcsolatát írják le [11]. Ezt a keretet az 1. ábra szemlélteti.
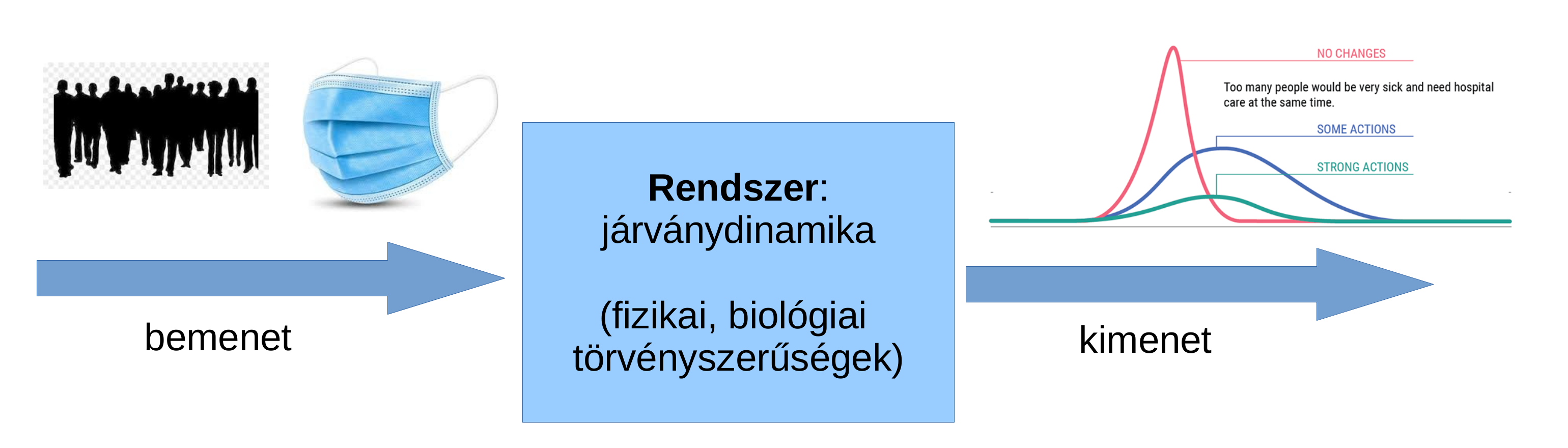
1. ábra: Járványdinamikához tartozó input-output modell
A beavatkozás szempontjából legfontosabb paraméter az egyszerű járványmodellünkben 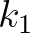 , amelyre lényeges hatást tudunk gyakorolni járványügyi intézkedések (pl. maszkviselés, távolságtartás, fokozott higiéniai előírások, népeség mobilitásának korlátozása) bevezetésével. A manipulálható nemnegatív és korlátos bemenet (
, amelyre lényeges hatást tudunk gyakorolni járványügyi intézkedések (pl. maszkviselés, távolságtartás, fokozott higiéniai előírások, népeség mobilitásának korlátozása) bevezetésével. A manipulálható nemnegatív és korlátos bemenet (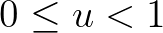 ) hatását érdemes
) hatását érdemes 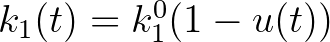 formában felírni, ahol
formában felírni, ahol 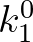 a szabad terjedéshez tartozó,
a szabad terjedéshez tartozó, 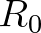 -lal arányos paraméter. Látni kell, hogy
-lal arányos paraméter. Látni kell, hogy 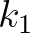 -et az emberi beavatkozástól független események is befolyásolhatják, pl. egy fertőzőképesebb mutáns megjelenése, ami gyakorlatilag önmagában oka volt a minden korábbinál nagyobb 3. hullámnak 2021 tavaszán. A befolyásolandó kimenet tipikusan az aktív fertőzöttek számától függő mennyiség, pl. az adott időpillanatban kórházban ápoltak száma. Rendszerelméleti szempontból talán nem kellőképpen sikerült tudatosítani a társadalommal a dinamika azon nemlinearitáson alapuló tulajdonságát, hogy az elkésett intézkedéseket a járvány szigorúan bünteti. Azaz egy megfelelően választott időponthoz képest akár néhány héttel később bevezetett korlátozás, lezárás azonos költséggel és társadalmi-gazdasági kárral szinte hatástalan lehet, mert a járvány előrehaladottabb állapotában a fékhatás már nagyon csekély. Ennek oka nemcsak a folyamat saját tehetetlensége, hanem főleg az, hogy a korlátos nagyságú bemenet (intézkedések) hatását a fertőzöttek növekvő száma közvetlenül befolyásolja, mégpedig számunkra kedvezőtlen irányban.
-et az emberi beavatkozástól független események is befolyásolhatják, pl. egy fertőzőképesebb mutáns megjelenése, ami gyakorlatilag önmagában oka volt a minden korábbinál nagyobb 3. hullámnak 2021 tavaszán. A befolyásolandó kimenet tipikusan az aktív fertőzöttek számától függő mennyiség, pl. az adott időpillanatban kórházban ápoltak száma. Rendszerelméleti szempontból talán nem kellőképpen sikerült tudatosítani a társadalommal a dinamika azon nemlinearitáson alapuló tulajdonságát, hogy az elkésett intézkedéseket a járvány szigorúan bünteti. Azaz egy megfelelően választott időponthoz képest akár néhány héttel később bevezetett korlátozás, lezárás azonos költséggel és társadalmi-gazdasági kárral szinte hatástalan lehet, mert a járvány előrehaladottabb állapotában a fékhatás már nagyon csekély. Ennek oka nemcsak a folyamat saját tehetetlensége, hanem főleg az, hogy a korlátos nagyságú bemenet (intézkedések) hatását a fertőzöttek növekvő száma közvetlenül befolyásolja, mégpedig számunkra kedvezőtlen irányban.
Beavatkozástervezés modell-prediktív szabályozással
Szabályozási célra egy SEIR modellnél kissé részletesebb, összesen 8 kompartmentből álló modellt használtunk [9], amelynek állapotátmeneti diagramja a 2. ábrán látható. Természetesen ez a modell is felírható kémiai reakcióhálózatként. A teljes populációnak ez a szintű felbontása már elegendő a legfontosabb szabályozási célok megfogalmazásához, és még hatékonyan kezelhető az elérhető számítási módszerekkel.
2. ábra: Szabályozási célra alkalmazott részletesebb kompartmentális model állapotátmenetei. A: fertőzésre fogékony, L: látens (még nem fertőz), P: preszimptomatikus (még tünetmentes, de már fertőz), A: tünetmentes fertőzött, I: tünetes fertőzött, H: kórházban ápolt fertőzött, R: gyógyult, D: elhunyt
Az irányítási célban minden esetben szerepelt a bevezetett intézkedések közvetlen káros hatásainak (azaz a bemenet valamely normájának) minimalizálása. Emellett fontos korlátozó feltételt jelentett az egy időben kórházban ápoltak számára előírt felső korlát, amelynek célja az egészségügyi rendszer túlterhelésének megakadályozása. Ezen túlmenően a vizsgált esettanulmányok alapvetően két részre oszthatók: mitigáció esetén a célok és korlátozások teljesítése mellett próbálunk együtt élni a járvánnyal, ahogy az a 2. és 3. hullámok esetén is történt, míg a szuppressziós (elnyomási) forgatókönyvnél a kórházban ápoltak számához és a halálozásokhoz tartozó norma is megjelenik a minimalizálandó célfüggvényben, ezáltal olyan szigorú korlátozások adódnak eredményként, mint a 2020-as tavaszi hullám során. Ezek a célok és korlátozások legcélszerűbben a modell-prediktív irányítási módszertan (MPC) keretében kezelhetők [7]. A tervezéshez segítségül hívtuk még az időfüggő temporális logikát, amely lehetővé teszi, hogy összetett (akár időfüggő logikai) specifikációkat is tömör formában meg tudjunk fogalmazni [1]. Ezekkel az eszközökkel a felírt szabályozási feladat automatikusan áttranszformálható egy vegyes egészértékű programozási problémává, amelyhez rendelkezésre állnak a nemlineáris dinamika kezelésére is alkalmas numerikus megoldók. Egy fontos gyakorlati problémát kellett még megoldanunk: a visszacsatolás tervezéséhez szükség van az egyes kompartmentekhez tartozó állapotokra (létszámokra), azonban ezek többsége a valóságban nem mérhető. Terveztünk tehát egy ún. állapotbecslőt, amely egyedül a kórházban ápoltak számát felhasználva képes aszimptotikusan megbecsülni a többi állapotváltozót. A 3. ábra egy olyan mitigációs szcenárió eredményét mutatja, ahol azt feltételeztük, hogy korlátozott ideig (3 hétig) 10.000 helyett 15.000 kórházi ágy áll rendelkezésre. A kezdőnap a 10. kórházban ápolt beteg regisztrációjának napja. A felső ábrán látható kb. 160 napos időtávon az állapotváltozók alakulása, a középső ábrán lévő nagyításban jobban látszik a kórházi ápoltak száma. Az alsó ábrán látható kék vonal mutatja a tervezett bemenetet (u), ahol a nagyobb érték szigorúbb korlátozó intézkedéseket jelent. A bemenet 0 értéke jelenti a korlátozások teljes feloldását, a 0.8 körüli érték pedig a pl. Kínában alkalmazott legszigorúbb lezárást. A piros vonal jelöli az időfüggő reprodukciós rátát, amely figyelembe veszi a fertőzésre fogékonyak létszámának csökkenését a járvány során. Látható, hogy a korlátozások feloldása után újabb járványhullám kezdődik, ahogy az a gyakorlatban sok országban be is következett 2020 őszén. Ennek kezelése újabb beavatkozás-tervezést igényel. Lényeges, hogy ezek a számítások még 2020 nyarán, jóval a 2. hullám előtt készültek.
3. ábra: Tervezett beavatkozás és hatása időben változó kórházi kapacitás esetén
Járványügyi adatok bányászata modell-inverzióval
Köztudott, hogy a hivatalos napi fertőzési számok csak a valós esetek töredékét tartalmazzák, és a gyógyultak nyilvántartása sem naprakész. Emiatt az ezekből az adatokból számolt járványgörbe nem tükrözi hitelesen a valódi helyzetet. A rendszer- és irányításelmélet egyik alapvető feladatosztálya a rendszerinverzió, ahol a megfigyelt kimenetből próbáljuk kiszámítani a bemenetet, és ebből gyakran még további állapotváltozókat is (amennyiben a rendszeroperátor invertálható és megfigyelhető). Esetünkben ez azt jelenti, hogy a leghitelesebb adatsornak tartott kórházi ápoltak számából mint kimenetből a modell dinamikájának figyelembevételével először becslést adtunk a látens fertőzöttek számának időbeli alakulására, és ebből állapotbecslővel számítottuk a többi kompartmenthez tartozó létszámokat. A főbb eredményeket a 4–7. ábrák mutatják. A kapott adatsorok természetesen érzékenyek a modell paramétereinek bizonytalanságára. Ezt a 7. ábrán illusztráljuk, ahol 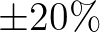 bizonytalanságot feltételeztünk az egyes modellparaméterekre.
bizonytalanságot feltételeztünk az egyes modellparaméterekre.
Összefoglalásként megállapítható, hogy a megfelelően paraméterezett klasszikus járványmodellek és az ismert rendszerelméleti módszerek alkalmasak a járványterjedési folyamatok analízisére, valamint az ezekkel kapcsolatos döntéstámogatásra. A modellek megbízhatóságának fenntartásához és növeléséhez viszont szükség van rendszeres és jól megtervezett járványügyi adatgyűjtésre (pl. [8]), amelynek összesített nyeresége biztosan sokszorosan meghaladja a költségeket.
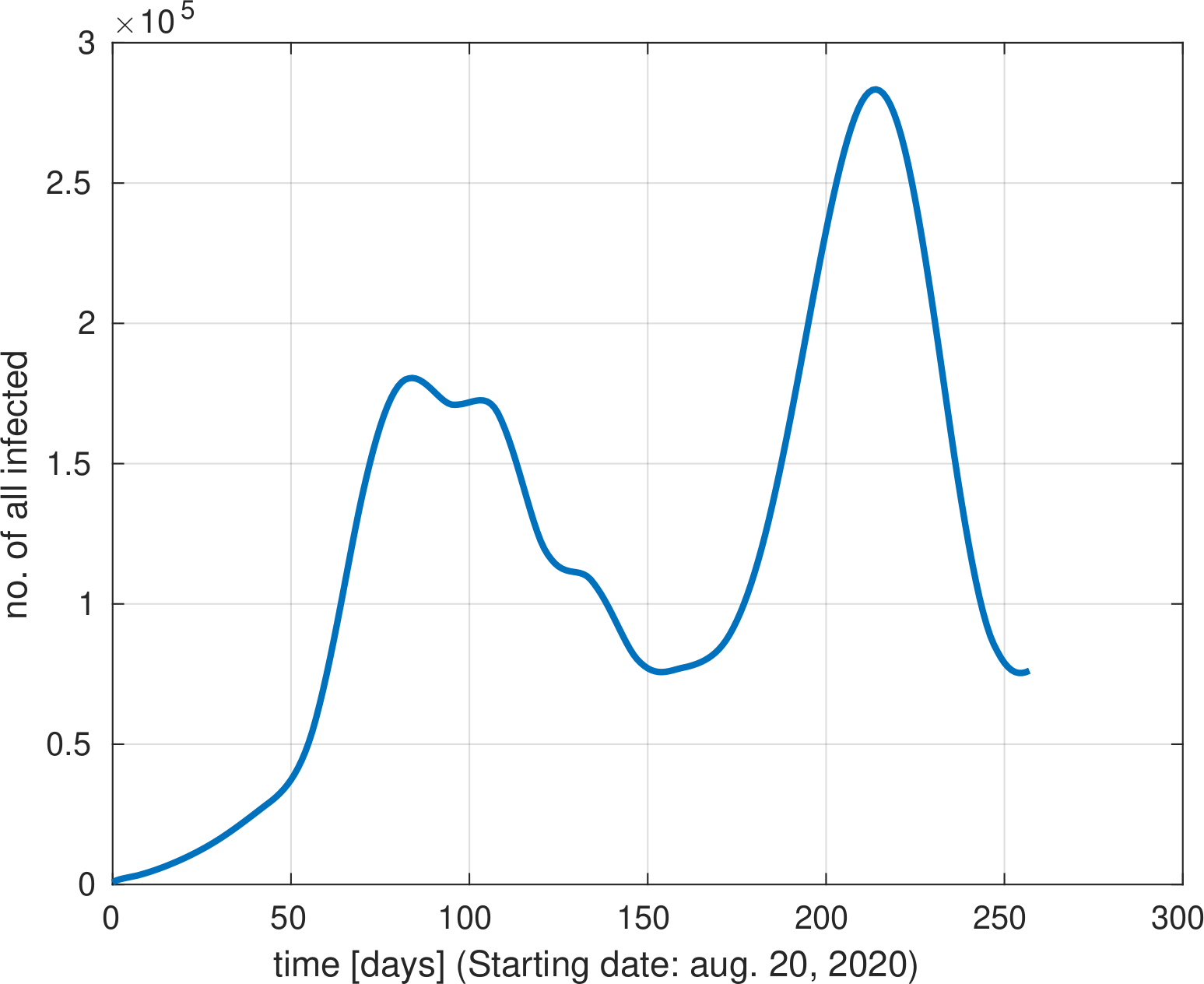
4. ábra: Az összes fertőzött (L, P, A, I, H) inverzióval becsült létszáma 2020. aug. 20-tól
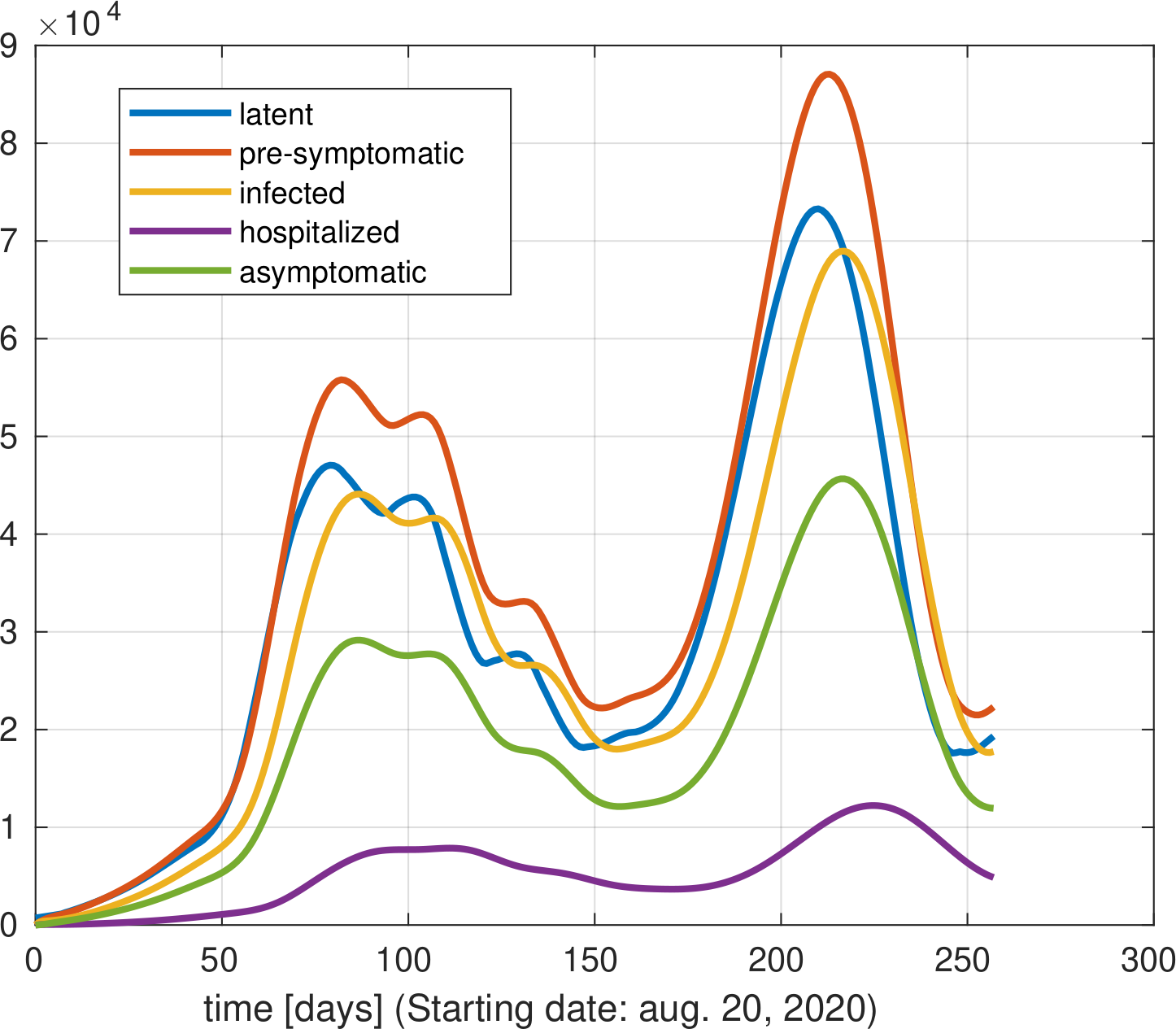
5. ábra: Az egyes kompartmentekhez tartozó inverzióval becsült létszámok 2020. aug. 20-tól
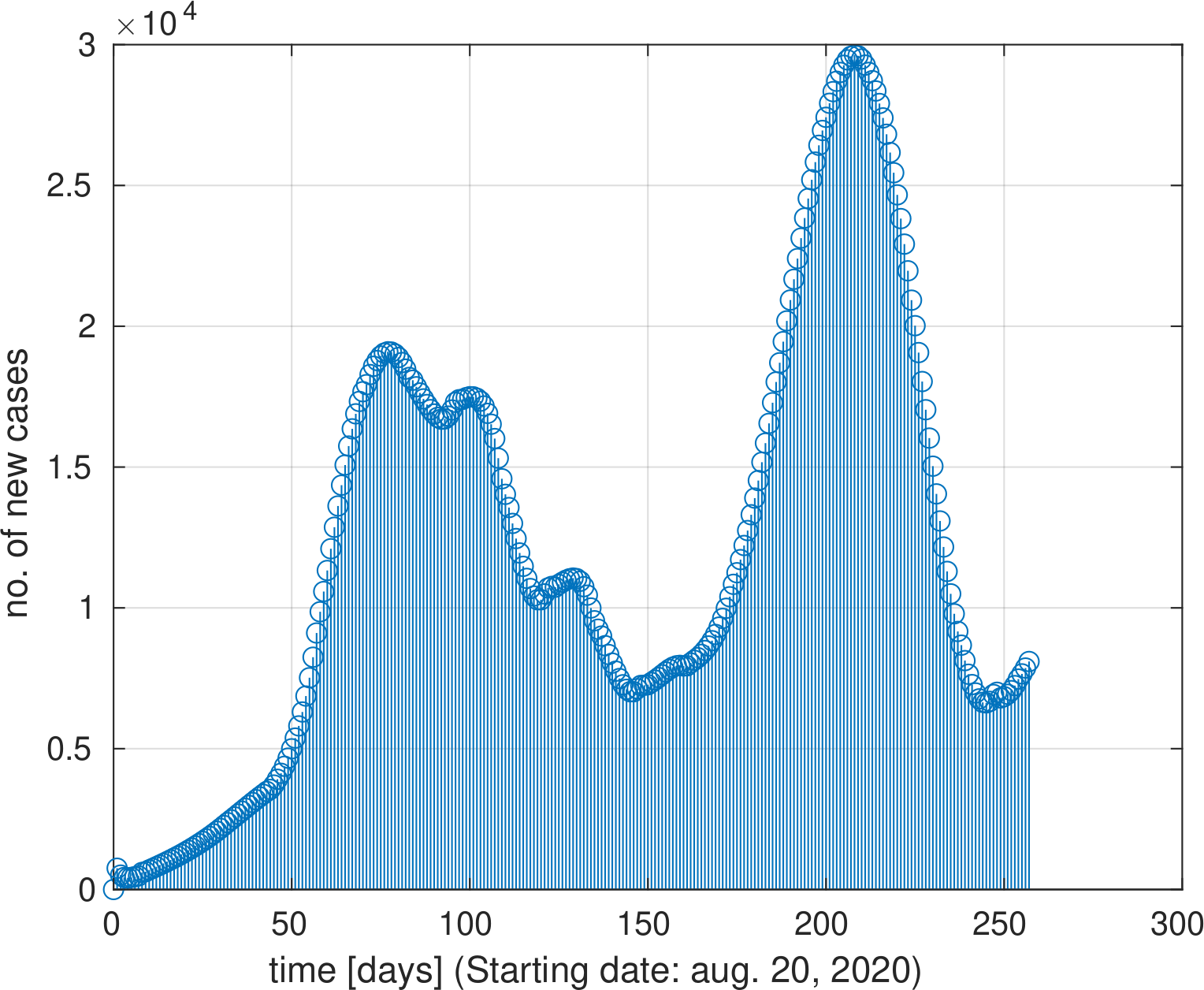
6. ábra: Inverzióval becsült napi új fertőzések száma 2020. aug. 20-tól
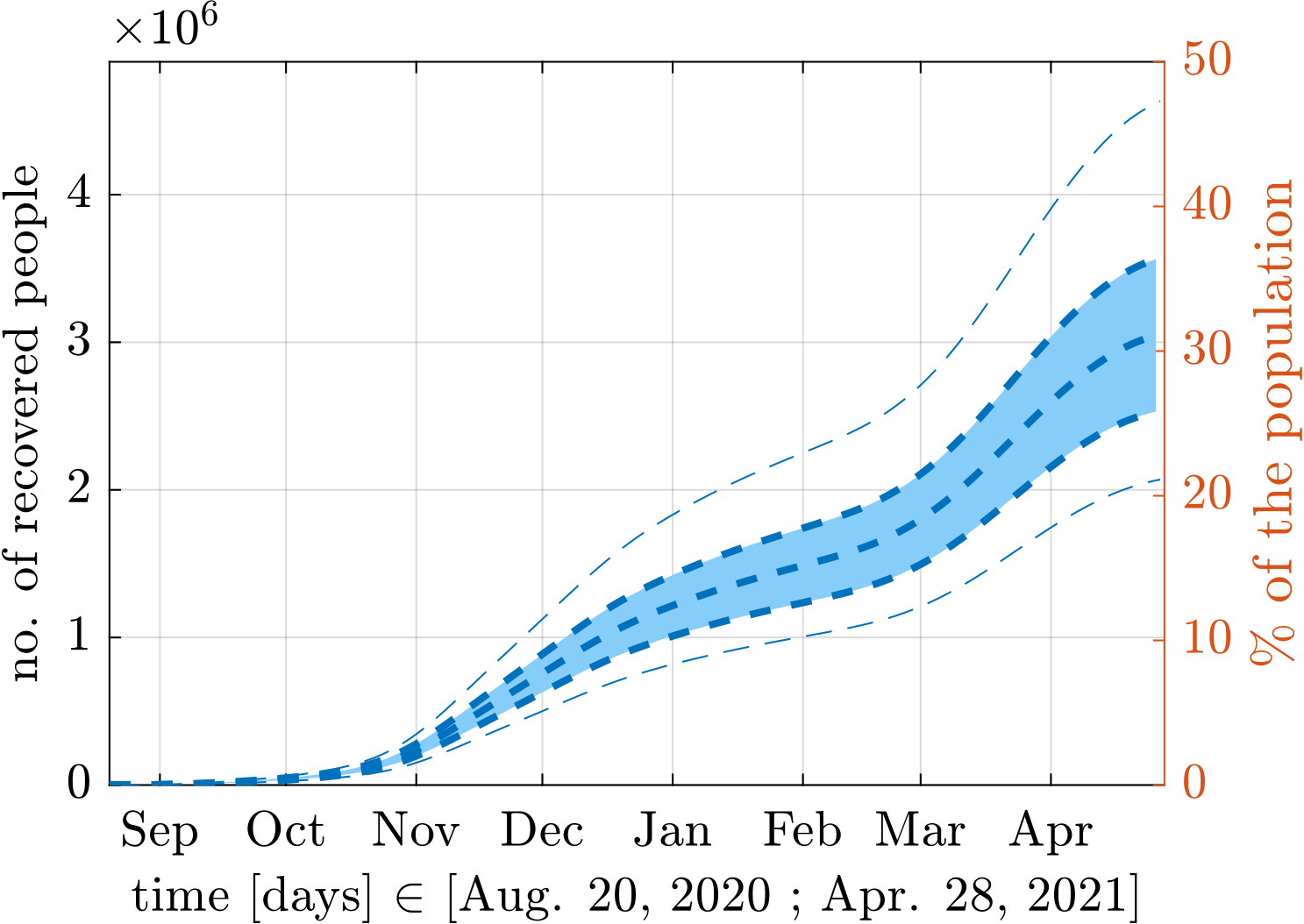
7. ábra: Fertőzésen átesettek inverzióval becsült száma bizonytalansági analízissel 2020. aug. 20-tól. A világoskék sáv a kapott szórást, a vékony kék szaggatott vonalak a kapott legkisebb és legnagyobb értékeket jelölik.
Köszönetnyilvánítás
A témakörben folytatott közös munkáért köszönetet szeretnék mondani társszerzőimnek és tanítványaimnak, Dr. Péni Tamásnak (ELKH SZTAKI), Dr. Röst Gergelynek (SZTE), Dr. Polcz Péternek (PPKE-ITK), Csutak Balázsnak (PPKE-ITK) és Horváth Gergelynek (PPKE-ITK).
Hivatkozások
[1] Calin Belta, Boyan Yordanov, and Ebru Aydin Gol. Formal methods for discrete-time dynamical systems, volume 15. Springer, 2017.
[2] Daryl J Daley and Joe Gani. Epidemic modelling: an introduction. Number 15. Cambridge University Press, 2001.
[3] Péter Érdi and János Tóth. Mathematical models of chemical reactions: theory and applications of deterministic and stochastic models. Manchester University Press, 1989.
[4] Martin Feinberg. Foundations of chemical reaction network theory. Springer, 2019.
[5] Wassim M Haddad, VijaySekhar Chellaboina, and Qing Hui. Nonnegative and compartmental dynamical systems. Princeton University Press, 2010.
[6] Thomas G Kurtz. The relationship between stochastic and deterministic models for chemical reactions. The Journal of Chemical Physics, 57(7):2976–2978, 1972.
[7] Jan Marian Maciejowski. Predictive control: with constraints. Pearson Education, 2002.
[8] Béla Merkely, Attila J Szabó, Annamária Kosztin, Ervin Berényi, Andor Sebestyén, Csaba Lengyel, Gergő Merkely, Júlia Karády, István Várkonyi, Csaba Papp, et al. Novel coronavirus epidemic in the Hungarian population, a cross-sectional nationwide survey to support the exit policy in Hungary. GeroScience, 42(4):1063–1074, 2020.
[9] Tamás Péni, Balázs Csutak, Gábor Szederkényi, and Gergely Röst. Nonlinear model predictive control with logic constraints for COVID-19 management. Nonlinear Dynamics, 102(4):1965–1986, 2020.
[10] Portfolio.hu. Ezrek életét menthetik meg a lezárások – a koronavírus modellezése egy virtuális városban, Jan 2021.
[11] Eduardo D Sontag. Mathematical control theory: deterministic finite dimensional systems, volume 6. Springer Science & Business Media, 2013.
Szederkényi Gábor
egyetemi tanár
PPKE-ITK









