Nullaíró verseny

Első nap (alfa-nap)

Akhilleusz és a Teknős újra találkoztak, és most sétálgatva beszélgetnek.

Akhilleusz: Kedves T. úr, emlékszik még a versenyfutásunkra?

Teknős: Már hogyne emlékeznék, kedves A. úr, azóta mi vagyunk a világ leghíresebb sportolói. Bár ön egyébként is híres. Mellékfoglalkozása: rövidtávfutó, főfoglakozása: hős.

Akhilleusz: Nem tagadom...

Teknős: Zénón jól kitalálta a versenyfutásunkat – csak nem úgy lett, ahogy elképzelte.

Akhilleusz: Rögtön utolértem magát – sőt meg is előztem.

Teknős: De azért érdekes volt az az elképzelése, hogy egyre csökken a távolságunk, és sosem fogy el.

Mostanában azon gondolkozom, hogy mekkora lehet a legkisebb távolság.

Akhilleusz: Nulla! Éppen akkor, amikor utolértem.

Teknős: A nulla távolság nem távolság. Úgy gondolom, hogy azért legyen valami kicsi.

Vajon a legkisebbek közül melyik a legkisebb?

Akhilleusz: Segítek magának: legyen ez a távolság mondjuk 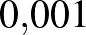$0{,}001$ m. Ez elég kicsi távolság.

Teknős: Milyen számrendszerben van ez a szám?

Akhilleusz: Tízes. Elvégre európaiak vagyunk.

Teknős: Miért a métert választotta?

Akhilleusz: Európaiak vagyunk.

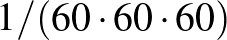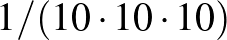Teknős: Azt azért megjegyezném, hogy kisebb a távolság, ha a méter helyett kisebb a mértékegység, és ha a számrendszer a 10-es helyett például a 60-as – mint a babiloniaké –, hiszen $1/(60\cdot 60\cdot 60)$ kisebb, mint $1/(10\cdot 10\cdot 10)$ .

De jó, egye fene, maradjon így – valóban európaiak vagyunk. Tehát legyen 1 milliméter.

Mármost tudok kisebb számot mondani: egyszerűen egy 0-t betoldok, és máris kisebb lesz a távolság.

Akhilleusz: Én meg kettőt toldok be: így 1 mikrométer lesz. De a továbbiakban ne említsük a mértékegységet, hiszen abban megegyeztünk. Maradjon csak maga a szám. Tehát a kis számunk legyen:

(Leírja.)

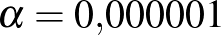
$\alpha=0{,}000001$

Teknős: Legyen... De kedves A. úr, miért választott görög betűt?

Akhilleusz: Miért? Miért?... Elvégre görögök vagyunk.

Teknős: Elvégre...

Akhilleusz: Úgy látom, újra versenyezhetünk: minél kisebb számot találunk ki, annál kisebb lesz a távolság.

Teknős: Valóban. Ez a verseny azonban soha nem érne véget. Mintha a kisiskolások vetélkednének, melyikük tud nagyobb számot mondani, és a következő egyszerűen hozzáadna 1-et.

Az első gyerek azt mondja: ezer, a második azt mondja rá: ezeregy. Az első azt mondja: végtelen, a második rávágja: végtelen 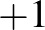$+1$ . Mire az első azt mondja: nem ér, ez butaság, a végtelen ugyanakkora, mint a végtelen 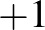$+1$ . Ebben megegyeznek. Unalmas ez a játék, inkább focizni mennek.

Mi is licitálhatnánk: melyikünk tud több 0-t írni az 1-es elé. Versenyfutás helyett verseny 0-írás lenne... Ez méltatlan hozzánk.

Akhilleusz: Igen, és csak csupa ilyen 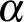$\alpha$ -szerű számokat kapnánk sok 0-val és a végén egy 1-essel.

Akkor hát egyezzünk meg döntetlenben.

Teknős: Egyelőre mást nemigen tehetünk. Hacsak nem... Még gondolkozom holnapig.

Remélem, holnap is találkozunk, kedves A. úr.

Akhilleusz: Én is remélem. Kellemesen elbeszélgettünk, kedves T. úr.

Második nap (béta-nap)

Akhilleusz és a Teknős újra találkoznak, és az üdvözlő szavak után folytatják az előző napi diskurzust.

Ahol a gyerekek abba szokták hagyni: a végtelennél, ők ott kezdik: Indul a Nullaíró verseny.

Teknős:

(Elővesz papírt és ceruzát a teknője alól, és ír egy számot. Felágaskodva Akhilleusz orra alá dugja.)

Kedves A. úr – mit szól ehhez?

Akhilleusz:

(Elgondolkodva nézi, aztán hitetlenkedve felkiált.)

Viccel velem?! Ilyen szám nincs!

Teknős: Már hogyne volna! Hiszen látja: leírtam, ott van az orra előtt. És amit egyszer a matematikában kitaláltak, és van benne rendszer, az van! Ahogy Hamlet beszédjéről mondja Polonius: „Őrült beszéd, őrült beszéd: de van benne rendszer.”

Nem csigázom tovább a kedves Olvasót. A cédulán ez a szám áll:

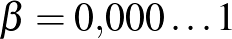
$\beta=0{,}000\ldots{} 1$

Akhilleusz: Ravasz: egyszerre beírt végtelen számú 0-t. A három pont ugye azt jelenti, hogy ott végtelen sok 0 van?

Teknős: Igen, azt.

Akhilleusz: De ha az emlékezetem nem csal: eddig úgy volt, hogy ezek a három pontok, amelyek a végtelen ismétlődést jelentik, mindig csak a számok végén voltak.

Teknős: Bizony, úgy volt... Eddig. Ez újdonság.

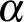De nézze csak: ez a $\beta$ szám sokkal kisebb a tegnapi $\alpha$ -nknál, még ha abba több ezer 0-t beleírtunk volna is.

Akhilleusz: Valóban: ez a tegnapi összes 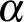$\alpha$ -féle számunknál is kisebb.

De árulja el nekem, miféle szám ez?

Teknős: Ez nem valós szám. Végtelenül kicsi szám, de nagyobb a 0-nál. Olyan kicsi, hogy az összes valós számnál kisebb. Van egy csúnyább neve is: infinitezimális szám – ez ugyanazt jelenti, mint a végtelenül kicsi. Ezt a szót még egyszer ki nem mondom: az előbb majdnem összegubancolódott a nyelvem. Bizony vannak végtelenül kicsi és végtelenül nagy számok is, de ezek nem valós számok.

Akhilleusz: És ezt maga találta ki, T. úr? Megemelem a kalapomat ön előtt – miket is beszélek –, a sisakomat.

Teknős: Túlbecsül engem... Természetesen nem én. Az amerikai Abraham Robinson és mások találtak ki hasonló újfajta számokat az 1950-es és 60-as években.

Akhilleusz: Nagyon érdekes... És mondja csak, ha most megnéznénk a 0-tól $\beta$ távolságra lévő pontot, hová rajzolná azt a számegyenesen?

Teknős: Ugyanoda, ahová a nullát – hiszen végtelenül közel van hozzá.

Akhilleusz: De ha volna egy nagyon erős nagyítónk – mondjuk ezerszeres nagyítással?... Vagy egy mikroszkópunk – milliószoros nagyítással?

Teknős: Mit sem érne: egy pontot látnánk.

De ha elővennénk egy végtelenszeres nagyítót, azzal már látnánk külön a $\beta$ pontot.

Akhilleusz: Végtelenszeres nagyítót?! Miket nem mond – T. úr?! Olyan nincs.

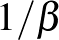Teknős: Ma már mondta azt a szót, hogy nincs. Az előbb már említettem, hogy végtelenül nagy nem valós számok is vannak. Például: ha $\beta$ végtelenül kicsi, akkor $1/\beta$ végtelenül nagy. Miért is ne lehetne ilyen nagyítónk? Vele láthatnánk a 0 végtelenül kicsi környezetét, és külön a 0-tól a $\beta$ -t.

Akhilleusz: És ha így nézzük, hol vannak a tegnapi 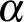$\alpha$ -szerű számaink – tehát a valós számok?

Teknős: Azok bizony végtelen távolságra kerültek jobbra.

Akhilleusz:

(A lábát nézve gondolkodva lépeget.)

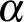Akkor én 0-ból indulva és $\beta$ -kat szökkenve hogyan érném utol magát, aki az $\alpha$ -ban van – vagyis nem éppen karnyújtásnyira? Végtelenszer kellene szökkennem?!

Teknős: Bizony, bármilyen gyorslábú is, sose érne utol.

(Magában morfondírozik: Hacsak nem... hacsak nem... növelné meg a sebességét végtelenre. De bolond lennék, ha ezt ma megmondanám neki. Ma végre én szeretnék futóbajnok lenni. Hangosan folytatja:)

Látom, ahogy a $\beta$ szám tetején ugrál a 0-kon az 1-estől a tizedesvessző felé...

Hiába. Futásban én győznék.

Akhilleusz: Elhiszem...

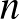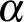Eszembe jutott valami: Honfi- és ókortársunk, Arkhimédész – az, aki kiugrott a fürdőkádból – axiómájában azt mondta: ha van egy kisebb távolságunk és egy nagyobb, akkor mindig találhatunk egy olyan $n$ természetes számot, amivel a kisebb távolságot megszorozva, túlhaladjuk a nagyobb távolságot. Ha $\beta$ a kisebb távolság, és $\alpha$ a nagyobb, akkor ez nem igaz.

Arkhimédész tévedett?

Teknős: Nem tévedett. Kijelentése igaz – a valós számokat tekintve. De ne feledje – a $\beta$ nem valós szám.

Arkhimédész korában nemigen foglalkoztak a végtelennel – lehet, hogy féltek tőle.

Akhilleusz: Én $\beta$ -ban, maga 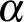$\alpha$ -ban... Mintha két különböző világban lennénk.

Teknős: Igen, úgy képzelje el: közöttünk lenne egy határvonal – egy limesz. Azon nem juthatna át.

Akhilleusz: Ezen még gondolkozom... Mindenesetre gratulálok, kedves T. úr. A legkisebb számért küzdő versenyünket megnyerte... Sőt még a futóversenyünket is!

De talán holnapra kitalálok egy még ennél is kisebb számot. Szöget ütött a fejembe, amit erről a két világról mondott... Ezzel a kis számával nagy követ dobott az állóvízbe... Már sejtem, hogy messzire érnek a hullámai.

Teknős: Alig várom a holnapot... és az ötletét.

Udvariasan elbúcsúznak egymástól.

Harmadik nap (gamma-nap)

Akhilleusz és a Teknős gyorsan köszönnek egymásnak; a Teknős a kíváncsiságtól mohón rögtön a tárgyra tér.

Teknős: Végiggondolta a tegnapi ötletét, kedves A. úr?

Akhilleusz: Bizony, és találtam egy 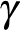$\gamma$ számot. Sokkal kisebb, mint a tegnapi $\beta$ .

Teknős: Mutassa gyorsan!

Akhilleusz:

(Elővesz egy cédulát a mellvértje alól, lehajolva megmutatja a Teknősnek. A cédulán a szám: 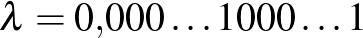$\lambda=0{,}000\ldots{} 1000\ldots{} 1$ )

Teknős: Érdekes szám, de úgy látom, hogy ez nem gamma, hanem lambda, és nem kisebb, mint a tegnapi béta... Visszafejlődünk, kedves A. úr?

Akhilleusz: Igaza van, hiszen a vak is látja, hogy ez nagyobb, hiszen a végét megtoldottam valamivel. De ez a toldalék nagyon kicsi lesz – ez lesz a 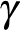$\gamma$ számom. Türelem, mindjárt megmutatom.

Teknős: Rendben – bár majd megesz a kíváncsiság.

Akhilleusz: Nos, rakjuk egymás mellé a két számot, és nézzük meg, hogy mennyivel nagyobb a 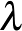$\lambda$ a $\beta$ -nál:

(Közben írja.)

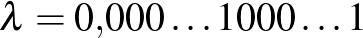
$\lambda=0{,}000\ldots{} 1000\ldots{} 1$

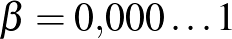
$\beta=0{,}000\ldots{} 1$

Végezzük el a kivonást, és megkapjuk a mai napra várt gammánkat:

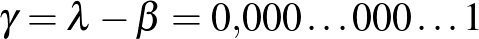
$\gamma=\lambda-\beta=0{,}000\ldots{} 000\ldots{} 1$

Mintha a 0-k közül kiszedtük volna az 1-est.

Teknős: A két végtelen 0-s sorozat egymás mellé került, tehát egyesíthetjük őket:

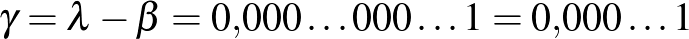
$\gamma=\lambda-\beta=0{,}000\ldots{} 000\ldots{}1=0{,}000\ldots{} 1$

De hiszen ez a mi $\beta$ számunk!

Vagyis azt kaptuk, hogy 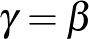$\gamma=\beta$ . Tehát, kedves A. úr, megállapíthatjuk, hogy tévedett: az ön mai 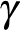$\gamma$ -ja nem kisebb az én tegnapi $\beta$ -mnál – hanem ugyanakkora.

Akhilleusz: Nem tévedtem. Hibát követett el, T. úr!

Teknős: Hogyhogy?!

Akhilleusz: Ahonnan kiszedtük az 1-est, ott maradt valami.

Teknős: Mi a csuda?!

Akhilleusz: Ott maradt a 0-k között egy láthatatlan választóvonal, és az megakadályozza, hogy a 0-kat csak úgy összevonjuk. Az ettől a határtól balra lévő 0-k nem ugyanolyanok, mint a jobbra lévők. Közöttük van a limesz... A két világ határa.

Mintha a végtelen számú 0-t megdupláztuk volna.

A végtelent szétbontva többnek látszik. Például a természetes számokat így is sorba állíthatjuk: 0, 1, 2, 3, 4, 5, 6, ..., de így is: 0, 2, 4, 6, 8, ..., 1, 3, 5, 7, .... Egy világból két világ lett: egy páros világ és egy páratlan világ.

Hogy a 0-k rendezettségét jól lássuk, sorszámozzuk, indexeljük őket:

(Írja.)

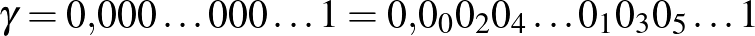
$\gamma=0{,}000\ldots{} 000\ldots{}1=0{,}0_00_20_4\ldots0_{1}0_30_{5}\ldots1$

Mit gondol, T. úr, miből van több: a páros számokból vagy a páratlan számokból?

Teknős: Nyilván ugyanannyian vannak.

Akhilleusz: És miből van több: természetes számokból vagy páros számokból?

Teknős: Ugyanannyi, hiszen a páros számokat megszámlálhatjuk a természetes számokkal...

Másféle szétbontások is lehetnek, például: 0, 3, 6, 9,12, ..., 1, 2, 4, 5, 7, 8, 10, ..., vagyis a 3-mal oszthatók, majd a nem oszthatók.

Akhilleusz: Vagy így: 0, 1, 4, 9, 16, ..., 2, 3, 5, 6, 7, 8, 10, 11, ....

Teknős: Látom: először a négyzetszámok, aztán a többi...

Itt jut eszembe: Galileo Galilei, a nagytekintélyű itáliai tudós a 17. század elején észrevette, hogy ugyanannyi négyzetszám van, mint ahány természetes szám, holott ritkábban vannak – de nem firtatta tovább ezt a problémát.

Akhilleusz: Mi firtassuk!

Teknős: Úgy látom, hogy a végtelent végtelenféleképpen bonthatjuk szét.

Akhilleusz: Lehet... Egyelőre maradjunk csak a két részre bontásoknál.

Ha csak kétfelé bontjuk – mint az előbbi esetekben –, akkor először elszámlálunk a végtelenig, majd a második számlálást 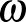$\omega$ -val kezdve még egyszer a végtelenig.

Vagyis a 0-inkat így is indexelhetjük, sorszámozhatjuk:

(Írja.)

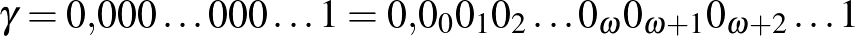
$\gamma=0{,}000\ldots{} 000\ldots{}1=0{,}0_00_10_2\ldots0_{\omega}0_{\omega+1}0_{\omega+2}\ldots 1$

Teknős: Azt hiszem, értem: a jobbra lévő rész egy újabb, még kisebb világ. A 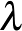$\lambda$ ezzel a toldalékkal végtelenül közel volt a $\beta$ -hoz, és a $\beta$ -t kivonva végtelenül közel kerültünk a 0-hoz. Sokkal közelebb, mint a $\beta$ .

Akhilleusz: Úgy van. Egy szinttel közelebb. Az én 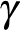$\gamma$ számom végtelenszer közelebb van a 0-hoz, mint a maga tegnapi $\beta$ -ja – tehát jóval kisebb.

Az előző bonyolult indexelés helyett – a rendezettséget és a határt azért mégis szemléltetve – a limeszt egy hullámos vonallal jelölöm; így a számom:

(Leírja a számot.)

$\gamma=0{,}000\ldots\wr 000\ldots{} 1$

Teknős: De már az én tegnapi $\beta$ számomnál is volt egy limesz. Az hol van?

Akhilleusz: Igaza van, azt is jelölöm. Tehát a mai szépen leírt 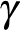$\gamma$ számom:

(Kijavítja a számot.)

$\gamma=0{,}000\ldots{} \wr 000\ldots{}\wr 1$

Teknős: Elfogadom. Ma én vesztettem...

De hogy vagyunk a távolságokkal? Vegyük csak elő a csodanagyítónkat és a számegyenest!

Akhilleusz: Nagyító nélkül nézve, vagy közönséges nagyítóval: 0, 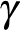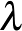$\gamma$ , $\beta$ , $\lambda$ egy pontban van, csak 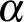$\alpha$ van jobbra.

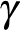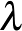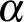A mágikus nagyítónkkal nézve: 0, $\gamma$ egy pontban van, jobbra egy másik pontban van $\beta$ , $\lambda$ , jobbra a végtelenben $\alpha$ .

Az így nagyított képünket nézzük meg másodszor is a nagyítónkkal, hogy végül végtelenszer kettő nagyítást kapjunk.

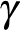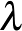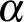Így nézve 0 környékét: a 0-tól jobbra látjuk $\gamma$ -t, jobbra a végtelenben $\beta$ , $\lambda$ van, még jobbra a második végtelenben $\alpha$ .

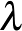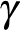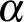Így nézve $\beta$ környékét: a $\beta$ -tól jobbra látjuk $\lambda$ -t, balra a végtelenben 0, $\gamma$ van, jobbra a második végtelenben $\alpha$ .

Teknős: Igen, magam is ugyanígy látom.

Akhilleusz: De akár a két nagyítót egyszerre egymás fölé téve is úgy látnánk, hiszen a nagyítások szorzódnak.

Teknős: Nem biztos.

Akhilleusz: Hogyhogy?

Teknős: Tőlünk függ – a képzeletünktől –, hogy milyen lencserendszert konstruálunk.

Lehet olyan, hogy a második lencse az első lencse által alkotott képet nagyítja: akkor a 0-tól a 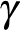$\gamma$ -t külön látjuk.

De olyan is lehet a lencserendszer, hogy csak egyszeres végtelen nagyítást kapunk.

Számolhatunk úgy, hogy: végtelenszer végtelen az végtelen a négyzeten.

De úgy is, ahogy a gyerekek számolnának: végtelenszer végtelen az végtelen.

Akhilleusz: Nem értem. Melyik a helyes?

Teknős: Mindkettő. Az utóbbi eset olyan, mint mikor én az imént a limeszt nem tekintve összevontam a 0-kat. Az első eset pedig, ahogy ön megtartotta a limeszt... De erre még később visszatérünk.

Akhilleusz: Állok elébe...

Teknős: Most pedig gratulálok: ma nyert, kedves Akhilleusz úr.

Holnap azonban folytathatjuk a még kisebb számok megtalálásának reményében. Már sejtem is, hogyan találhatok még kisebbet.

Akhilleusz: Nekem is vannak elképzeléseim róla, kedves Teknős úr.

Holnap akkor a delta következik... Vajon melyikünk 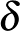$\delta$ száma lesz kisebb?

Búcsút vesznek egymástól.

Negyedik nap (delta-nap)

Akhilleusz és a Teknős kölcsönös üdvözlések után folytatják az eszmecseréjüket.

Akhilleusz: Találtam egy 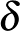$\delta$ számot, és sokkal kisebb a tegnapi 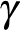$\gamma$ -nál. Leírtam.

Teknős: Én is.

Akhilleusz: Akkor nézzük!

(Előveszik a papírdarabjukat, és megmutatják egymásnak.

Mindkettőn pontosan ugyanaz a szám áll:)

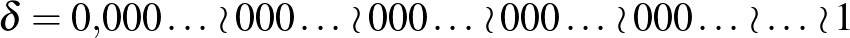
$\delta=0{,}000\ldots{} \wr 000\ldots{}\wr 000\ldots{} \wr 000\ldots{} \wr 000\ldots{} \wr \ldots{} \wr 1$

Teknős: A nagy szellemek találkozása.

Akhilleusz: Azért ne bízzuk el magunkat! Nem is volt olyan nehéz kitalálni.

Teknős: Egy kicsit beszéljük meg ezt a számot! A végső három pont azt jelenti, hogy a végtelen 0-s sorozatok végtelenszer ismétlődnek, tehát 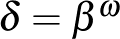$\delta=\beta^{\omega}$ .

Akhilleusz: Igen. És tegnap óta tudjuk, hogy a 0-s sorozatokat nem vonhatjuk össze.

Teknős: Úgy van. Azért írtuk be az ön tegnap kitalált limesz jeleit.

Akhilleusz: És hogyan látjuk a számegyenesen ezt a 0-tól különböző a 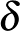$\delta$ számot?

Teknős: Egyszerű: egymás után végtelenszer nagyítunk a végtelenszeres nagyítónkkal...

Akhilleusz: Érdekes ez a területünk a tizedesvessző és a végén lévő 1-es között. Mintha egyre csak újabb és újabb 0-k jönnének bele, és el kell helyeznünk benne mindegyiket. Egy hotelra emlékeztet, ahová egyre csak jönnek a vendégek, és mindegyiket fogadni kell. Hallottam, hogy van ilyen hotel – és nincs is messze.

Teknős: Nagyszerű ötlet! Valóban ugyanolyan a struktúrája, a rendezettsége, mint a miénknek, vagyis a mi görög szavunkkal élve: izomorfizmust talált, kedves A. úr. A hotelt Hilbert német matematikus találta ki a 20. század elején. Ez is gondolatkísérlet, mint a mi versenyfutásunk. Itt van a hotelja a közelben.

Egy pincér ismerősöm ott dolgozik. Odasétálhatnánk.

Akhilleusz: Rajta, menjünk!...

Egy nagy hotel előtt megállnak. A nagyméretű buszok sora a horizontig ér.

A bejáratnál tábla:

HILBERT GRAND HOTEL

IGAZGATÓ: DAVID HILBERT

MINDIG VAN SZABAD SZOBÁNK.

MINDEN VENDÉGET SZÍVESEN VÁRUNK!

Teknős: Az ismerősöm igen szószátyár: mindig mindent tudok a szálló belső ügyeiről.

Akhilleusz: Mikor jöttek a vendégek?

Teknős: Ma délelőtt.

Akhilleusz: Hány szobája van a szállodának?

Teknős: Végtelen sok.

Akhilleusz: Hány busz érkezett ide?

Teknős: Végtelen sok.

Akhilleusz: És egy buszban hányan voltak?

Teknős: Végtelen sokan.

Akhilleusz: Úgy tűnik, mindenki bement, és kapott szobát. Az igazgató ötletesen elrendezte. Mint ahogy mi is befogadtuk az újabb és újabb 0-kat.

Teknős: Úgy van. És ahogy a mi 0-ink szépen, katonásan sorban vannak, itt is az igazgató szigorúan betartatta a rendet.

Akhilleusz: Mi volt a rend?

Teknős: Sorban jöttek a buszokról az emberek. A vendéget fogadták a recepción, mindegyikük kapott egy cédulára írva két számot: az egyik volt a sorszáma – hogy hányadikként érkezett –, ez lett az azonosítója, valamint megkapta a szobaszámát is, amelyet a sorszámából számoltak ki; a londinerek fogták a vendégek csomagjait, és elkísérték őket a szobájukig.

Akhilleusz: Hogyan kapták a sorszámokat?

Teknős: Az első busszal kezdték. Így kapták a sorszámokat: 0, 1, 2, 3, 4 stb.

Akhilleusz: És a második busz utasaival hogyan folytatták?

Teknős: 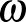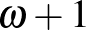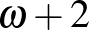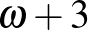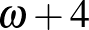$\omega$ , $\omega+1$ , $\omega+2$ , $\omega+3$ , $\omega+4$ és így tovább.

Akhilleusz: Értem... Átléptek egy limeszen.

És az a gyerek, aki azt mondta, hogy a végtelen 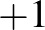$+1$ nagyobb, mint a végtelen, nem is mondott butaságot.

Teknős: Nem – legalábbis, ha a sorszámokat nézzük.

De ha azt nézzük, hogy hányan lettek a szállodában, akkor a végtelen 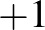$+1$ ugyanakkora, mint a végtelen. Mindkét gyereknek igaza lehet. Attól függ, hogy mi a szám funkciója. Erről még majd fogunk beszélni.

Akhilleusz: A második busz első utasa tehát az 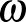$\omega$ számot kapta. Előtte volt a sorban az első busz utolsó utasa. Ugye az ő sorszáma 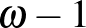$\omega-1$ lett?

Teknős: Értelmetlen a kérdése! Már ne haragudjon, kedves A. úr, de ön badarságokat beszél.

Visszakérdezek: Van-e az első busznak utolsó utasa?

Akhilleusz: Nincs.

Teknős: Akkor utolsó sorszám sem lehet. A sorban nincs senki a második busz első utasa előtt – bár ő megelőzi az első busz összes utasát... Különleges személy. Az 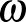$\omega$ sorszámnak nincs előzménye, ahogy a 0-nak sem.

Akhilleusz: Belátom: tévedtem.

(Kajánkodik.)

És mi lett a sorszáma az utolsó busz első utasának?

Teknős: Értem a tréfát! Utolsó busz sincs. Az utolsó busz utasainak sorszámairól nem beszélhetünk.

Akhilleusz: Jól van, komolyabb leszek...

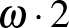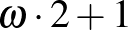Megmondom, mi a sorszáma a 3. busz első utasának: $\omega\cdot 2$ , a második utasának: $\omega\cdot 2+1$ .

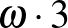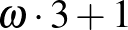Továbbá: a 4. busz első utasának: $\omega\cdot 3$ , a második utasának: $\omega\cdot 3+1$ .

És így tovább...

Teknős: Úgy van.

Akhilleusz: És mi van a szobaszámokkal? Hogy számolták ki?

Teknős: Nagyon egyszerűen: Összefésülték a sorszámokban lévő számok számjegyeit.

Akhilleusz: Láthatnék egy példát?

Teknős: Jó. Vegyük a 2073. busz 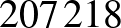$207\,218$ . üléséről jött utast.

Sorszáma: 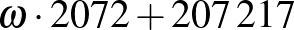$\omega\cdot 2072+207\,217$ .

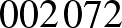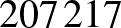A számokat kezdő 0-k betoldásával azonos hosszúságúra hozzuk: $002\,072$ és $207\,217$ .

A számjegyeket összefésüljük: 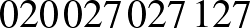$020\,027\,027\,127$ .

A kezdő 0-t elhagyhatjuk, így a szobaszáma 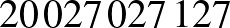$20\,027\,027\,127$ lesz.

Akhilleusz: Egyszerű. És úgy látom, hogy minden szobába jutott valaki, vagyis a hotel megtelt.

Az igazgató megnyugodhatott: mindenkit szépen fogadni tudott.

Ebben a szállodában valóban nagy a rend.

Teknős: Köznapi szóval: jól rendezett... Matematikai szakszóval: jólrendezett.

Akhilleusz: Mi is megnyugodhatunk: jól elrendeztük a 0-inkat...

Akkor azt hiszem, mára be is fejezhetjük. Nem tudok kisebb számot kitalálni.

Teknős: Én sem.

Akhilleusz: Akkor befejeztük a versenyt.

Teknős: Be... Az eredmény: döntetlen.

Akhilleusz: Magam is úgy vélem. Megegyeztünk.

Teknős: Holnap azért még összefutunk.

Akhilleusz: Én szó szerint futva jövök.

Búcsút intenek egymásnak.

Ötödik nap (epszilon-nap)

A Teknős már a találkozóhelyen, Akhilleusz futva érkezik.

Akhilleusz: Üdv!

Teknős: Üdv!

Akhilleusz:

(Helyben fut.)

Edzhetek tovább, kedves T. úr? Ugye nincs kisebb szám?

Teknős: Van.

Akhilleusz:

(Földbe gyökerezik a lába.)

Ne vicceljen!

Teknős: Képzelje, a pincér ismerősöm mesélte, hogy az éjszaka jött egy újabb vendég a szállodába.

Akhilleusz: És?... Mi történt?...

Teknős: A recepción rázni kezdte csengőt, mire előjött a személyzet. Közölték vele, hogy megtelt a szálló, nem tudnak mit tenni. Az újonnan érkezett hivatkozott a bejárati táblára, szó szót követett; követelte, hogy ébresszék fel az igazgatót.

Akhilleusz: De honnan jött ez az ember – hiszen a buszokból már mindenki kiszállt?

Teknős: Azt mondta, hogy egy másik buszkonvojjal érkezett, amelyik éppen akkora, mint a hotel előtt parkoló konvoj – és annyian jönnek még a buszokból, mint ahányan már a szállodában alszanak.

Akhilleusz: És?... Jött az igazgató?...

Teknős: Jött, és rögvest intézkedett: A felháborodott utas megkapta az 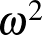$\omega^2$ sorszámot, a többiek az 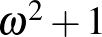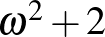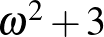$\omega^2+1$ , $\omega^2+2$ , $\omega^2+3$ , ... sorszámokat, és mindenkit el tudtak szállásolni.

Akhilleusz: Értem. És ha jött volna egy harmadik konvoj, akkor a konvoj első buszának az első utasa az 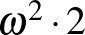$\omega^2\cdot 2$ sorszámot kapta volna.

Teknős: Úgy van.

Akhilleusz: És a szobaszámok?... Hiszen tele van a szálló.

Teknős: A szobaszámaikat most a 3 szám számjegyeinek összefésülésével generálták.

Például a második konvoj 2223. buszának 778. utasának sorszáma:

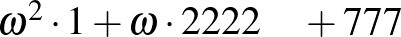
$\omega^2\cdot 1+\omega\cdot 2222 \quad +777$

A három számot kezdő 0-k betoldásával azonos hosszúságúra hozzuk: 0001 és 2222 és 0777

A számjegyeket összefésüljük: 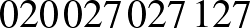$020\,027\,027\,127$

A kezdő 0-t elhagyhatjuk, így a szobaszáma 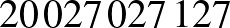$20\,027\,027\,127$ lesz.

Akhilleusz: Viszont ott már aludt valaki! Nézzük meg a sorszámát! Ott van a céduláján, de a szobaszámából is vissza tudom fejteni: a 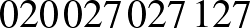$020\,027\,027\,127$ szobaszámot szétfésülve: az 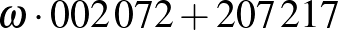$\omega\cdot 002\,072+207\,217$ sorszámú. Már emlékszem: ő szerepelt a tegnapi példánkban.

Teknős: Sajnos mindenkit fel kellett ébreszteni az éjszaka kellős közepén, és megkérni őket, hogy fáradjanak át egy másik szobába, hogy az újonnan jöttek is beköltözhessenek.

Akhilleusz: Kiszámolom, hová költöztették át a példánkban szereplő vendéget:

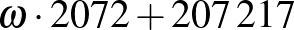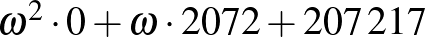Sorszáma $\omega\cdot 2072+207\,217$ , vagyis most kiegészítve: $\omega^2\cdot 0+\omega\cdot 2072+207\,217$ .

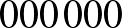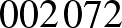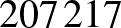Kezdő 0-k betoldásával az azonos hosszúságú számok: $000\,000$ és $002\,072$ és $207\,217$ .

A számjegyeket összefésüljük: 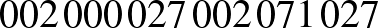$002\,000\,027\,002\,071\,027$ .

Vagyis az új szobaszáma 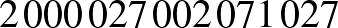$2\,000\,027\,002\,071\,027$ lett, a céduláján átírták a régi 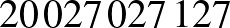$20\,027\,027\,127$ szobaszámát erre, majd átköltöztették. A sorszáma természetesen maradt, hiszen az a vendég személyi azonosító száma.

Jól számoltam?

Teknős: Jónak látom.

Akhilleusz: Mi hogyan csináljuk, ha még egyszer annyi 0-t akarunk berakni?

Teknős: Egyszerű: A tegnapi 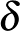$\delta$ számunknál a tizedesvessző és az 1-es közötti részt betoldjuk még egyszer mögéje – keletkezik egy újabb fajta limesz a közepénél, amit lyuggatott vonallal (három egymás fölötti ponttal) jelölök.

(Írja.)

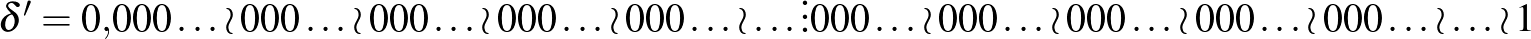
$\delta'=0{,}000\ldots\wr 000\ldots\wr 000\ldots\wr 000\ldots\wr 000\ldots\wr \l... ...ts 000\ldots\wr 000\ldots\wr 000\ldots\wr 000\ldots\wr 000\ldots\wr \ldots\wr 1$

Akhilleusz: Értem... Csak kezd áttekinthetetlenné válni. Találjunk ki valamilyen egyszerűbb írásmódot!

Mi lesz, ha jön még egy buszkonvoj?... És mi lesz, ha végtelen számú buszkonvoj jön?...

Teknős: Igaza van, A. úr. A végtelenül ismétlődő számsorozatokat felülhúzással is szokták jelölni: a végtelenül ismétlődő szakaszt felül egy vonallal összekötjük, például:

(Írja.)

$1/3=0{,}333\ldots{}=0{,}\overline{3}$

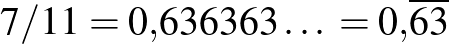
$7/11=0{,}636363\ldots{}=0{,}\overline{63}$

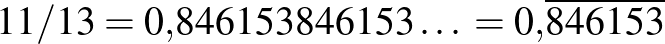
$11/13=0{,}846153846153\ldots{}=0{,}\overline{846153}$

Akhilleusz: Nézzük meg, hogyan írhatjuk így az eddigi számainkat!

(Írja.)

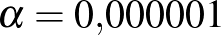
$\alpha=0{,}000001$

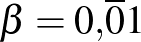
$\beta=0{,}\overline{0}1$

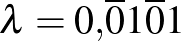
$\lambda=0{,}\overline{0}1\overline{0}1$

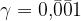
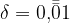
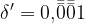
Teknős: Nagyon jó... És már a limesz jeleinkre sincs szükség.

Akhilleusz: Pörgessük föl a képzeletünket: Ha végtelen sok buszkonvojunk jött volna, akkor azoknak az elszállásolása után a következő különleges vendég az 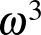$\omega^3$ sorszámot kapta volna, hiszen az előtte kiadott sorszámok: a végtelen konvoj szorozva a végtelen busszal szorozva a végtelen utassal.

A mi ennek megfelelő nagyon kicsi számunk pedig:

(Írja.)

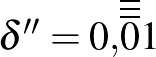
$\delta''=0{,}\overline{\overline{\overline{0}}}1$

Teknős: Pontosan. Nagyon jól számol, kedves A. úr... És nagyon jól látszik az azonosság – az izomorfizmus... Végtelen buszkonvoj kitesz egy buszármádiát stb... Elfogy rájuk a szó.

Akhilleusz: Tehát fokozhatjuk: Ezeket a felülhúzásokat megismételhetjük végtelenszer is.

Teknős: Miért ne!

Akhilleusz: Írom is... Micsoda pech! Annyit írtam, hogy betelt a papírom.

(A pajzsa belső zsebéből elővesz egy kütyüt. Hosszasan bíbelődik vele, aztán fel-, vagyis inkább lemutatja a számot a Teknősnek:)

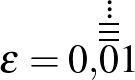
$\varepsilon=0{,}\dot{\dot{\dot{\overline{\overline{\overline{0}}}}}}{1}$

Teknős: Nagyszerű!... Legkisebbszerű!

Legyen ez a legkisebb szám, amit le tudunk írni... Talán egyéb trükkökkel lehetne még kisebb számokat találni, de mi itt most álljunk meg.

Akhilleusz: Jó, legyen ez a legkisebb számunk... De hogyan képzeljük el?

Teknős: A 0-k végtelen sorozatainak végtelenszer egymásba ágyazott rendszere... Végtelen sok egymásba végtelenszer bepakolt matrjoska baba...

Talán így... Valami ilyesmi... Nehéz elképzelni...

Akhilleusz:

(Hahotázik.)

Hahaha... határtalanul halmozódó hatalmas hierarchia.

Teknős: Vicces, de pontos.

Akhilleusz:

(Komolyra fordítja a szót.)

Akkor végleg fejezzük be a versenyünket.

Hirdessünk végső eredményt:

Ön nyert, Teknős úr!

Teknős: Nem tekinthetem magam győztesnek, hiszen az ön gamma számánál elkövettem azt a hibát, hogy a 0-kat összevontam. A gamma számhoz ön jutott el azzal, hogy észrevette a limeszt. A felismerése nélkül végképp elakadtunk volna. Onnan már könnyebben folytathattuk.

Akhilleusz: Igaz... a gamma az én érdemem.

Teknős: Azon kívül rájött a Hilbert hotellal való izomorfizmusra.

Akhilleusz: Ez is igaz.

Teknős: Végül a végső számot, az epszilont is ön írta le.

Akhilleusz: Igaz. Kitalálni könnyű volt... De leírni a szövegszerkesztővel?! Macerás.

Teknős: Akkor maga nyert megint, kedves Akhilleusz úr.

Akhilleusz: Dehogyis. Hálás vagyok, hogy sok mindenre rávezetett.

Egyezzünk meg döntetlenben, kedves Teknős úr.

Teknős: Rendben. Megegyeztünk...

Akhilleusz: Úgy érzem, hogy még mindig csak az első lépéseket tettük meg a legkisebbek felé.

Teknős: Én is... Bár átléptünk a valós számok adta korlátokon, maguknak a számoknak a használata akadályt okozhat.

Akhilleusz: Igen... Hogyan írhatnánk le a számoknál is kisebb kisebbeket?

Teknős: Nem tudom... De biztos, hogy a számokon túl is lehet még kicsinyíteni.

Magukba merülve elindulnak a hotel felé...

Epilógus (még az epszilon-nap)

Akhilleusznak eszébe jut valami.

Akhilleusz: Álljunk meg egy szóra! Hogyan növekedhetnek tovább a vendégek sorszámai?

Teknős: Mindjárt leírom. Az egészet Georg Cantor német matematikus találta ki a 19. század végén. Sok mást is kitalált... A halmazelmélet megalapozója. Megnyitotta az utat a végtelenekkel való számoláshoz – emiatt sok kritika is érte. Sajnos az élete utolsó kb. 20 évében egyre gyakrabban kellett szanatóriumba vonulnia.

Akhilleusz: Olyan veszélyes a végtelenekkel foglalkozni? Akkor jobb, ha abbahagyjuk.

Teknős: Lehet, hogy egy kicsit veszélyes.

Mi, ókori görögök – talán Zénónt kivéve – óvakodtunk is a matematikai végtelentől. Szinte tiltott terület volt. Például Eukleidész, miután elegánsan bebizonyította, hogy végtelen sok prímszám van, ezt így soha le nem írta volna – helyette óvatosan így fogalmazott: „A prímszámok darabszáma nagyobb bármely adott számnál.”

Viszont éppen ez a terület a matematika legszebb része. Lám, mi is milyen jól elszórakozunk vele.

Akhilleusz: A tudás élvezete... Az alma a fáról.

Teknős: Úgy van! Hilbert mondta: „Senki sem űzhet ki minket abból a paradicsomból, melyet Cantor teremtett nekünk.”

No, de térjünk vissza akkor a kérdésére, kedves A. úr: nézzük meg a sorszámokat.

Cantor ezeket ordinális számoknak nevezte el, magyarul rendszámnak nevezzük.

Észrevette, hogy a természetes számoknak (1, 2, 3, 4, ... vagy 0, 1, 2, 3, 4, ...) kétféle szerepük lehet - két számsort képezhetünk:

Kardinális számok – hány elem van egy halmazban: egy, kettő, három...
Rendszámok – hányadik egy jólrendezett halmazban: első, második, harmadik...

Ha tudjuk, hogy rendszámról van szó, akkor az -ik végződéseket el is hagyhatjuk, mint például a vendégek céduláján.

Akhilleusz: Hisz ezeket a számsorokat minden gyerek ismeri. Mi ebben az új?

Teknős: Ha végesek a számok, akkor valóban pofonegyszerű. De ha végtelenek, akkor a kétféle számok egészen eltérő módon viselkednek.

Akhilleusz: Akkor mutassa kérem, hogyan növekednek a rendszámok.

Teknős: Néhányat leírok:

(Írja.)

0, 1, 2...

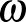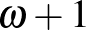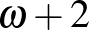$\omega$ , $\omega+1$ , $\omega+2$ , ...

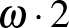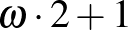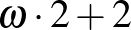$\omega\cdot 2$ , $\omega\cdot 2+1$ , $\omega\cdot 2+2$ , ...

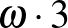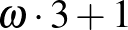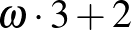$\omega\cdot 3$ , $\omega\cdot 3+1$ , $\omega\cdot 3+2$ , ...

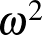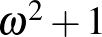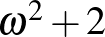$\omega^2$ , $\omega^2+1$ , $\omega^2+2$ , ...

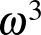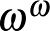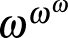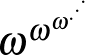
$\omega^3$ , ... $\omega^{\omega}$ , ... $\omega^{\omega^{\omega}}$ , ... $\omega^{\omega^{\omega^{.^{.^{.}}}}}$

Akhilleusz: A végén az a három pont azt jelenti, hogy a hatványozást a végtelenig folytatjuk?

Teknős: Igen... Ez hasonlít a mi végtelen felülhúzásainkra. Látszik az izomorfizmus.

Ezt az 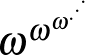$\omega^{\omega^{\omega^{.^{.^{.}}}}}$ számot Cantor elnevezte 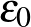$\varepsilon_0$ -nak. Ez a nagy szám még megszámlálható végtelen.

Még folytatta, de mi most ne folytassuk. (Lehetne még például 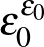$\varepsilon_0^{\varepsilon_0}$ és hasonlók, majd egy nagy ugrás után 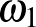$\omega_{1}$ , de az már megszámlálhatatlan végtelen.)

Ha a ma kitalált legkisebb számunkat, az 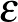$\varepsilon$ -t meg akarnánk látni a számegyenesen 0-tól különálló pontként, akkor egymás után 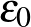$\varepsilon_0$ -szor kellene nagyítanunk a végtelenszeresen nagyítónkkal...

És ha jól számolok, a számunk: 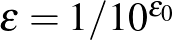$\varepsilon=1/10^{\varepsilon_0}$ .

Akhilleusz: Megszámlálható és megszámlálhatatlan végtelen... Azt hiszem, mi eddig csak a megszámlálható végtelenekkel foglalkoztunk. Van olyan végtelen is, amelyik megszámlálhatatlan?

Teknős: Van, és annak még sokkal több eleme van. Például egy szakasz pontjainak száma...

A halmazoknak a számosságai a kardinális számok, azaz hány elemük van.

Az összes megszámlálható végtelen azonos számosságú: éppen annyi eleme van, mint ahány természetes szám van. Ez a legkisebb számosságú végtelen, kardinális számként ezt is 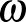$\omega$ -val jelölhetjük, de Cantor erre bevezette a héber ábécé első betűjét használva az 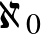$\aleph_0$ - kimondva alef null - jelölést. Mondhatjuk, hogy az 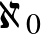$\aleph_0$ lánykori neve az 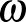$\omega$ . 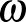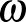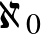Használjuk az $\omega$ -t inkább csak rendszámként, és $\omega$ számossága $\aleph_0$ .

Tovább mennek a szálló felé...

Akhilleusz: Hogyan számolhatunk a végtelenekkel?

Teknős: Csak az összeadásra mutatok néhány egyszerű példát:

(Írja.)

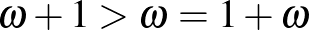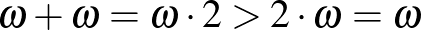Rendszámok:	$\omega+1>\omega=1+\omega$	$\omega+\omega=\omega\cdot 2>2\cdot \omega=\omega$
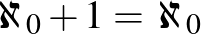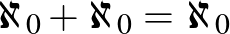Kardinális számok:	$\aleph_0+1=\aleph_0$	$\aleph_0+\aleph_0=\aleph_0$

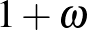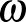Akhilleusz: $1+\omega$ miért $\omega$ ?

Teknős: Képzelje el, hogy a szállóba érkezik először egy vendég: a 0 sorszámot kapja, majd a busszal érkező végtelen sok új vendég rendre megkapja a sorszámát: 1, 2, 3, 4, ..., vagyis ugyanolyan, mintha mindenki egyszerre érkezett volna.

Akhilleusz: Értem... Egy kicsit nézzük meg a megszámlálhatatlan végteleneket is.

Teknős: Az elemeik olyannyira folytonosan egymás mellett vannak, mint például egy szakasz pontjai, vagy a valós számok, hogy nem tudjuk számlálni őket. Ezeket a végteleneket a folytonosságuk miatt – megint görög szót használva – kontinuum végtelennek nevezzük, számosságukat a gótikus 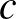$c$ betűvel jelöljük.

Megszámlálható: a por. Megszámlálhatatlan, kontinuum: a méz.

A legkisebb megszámlálhatatlan végtelen számossága 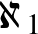$\aleph_1$ (alef 1).

A megszámlálhatatlan végtelenekből végtelen sok van, számosságukat Cantor így jelölte: 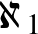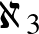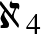$\aleph_1$ , $\aleph_2$ , $\aleph_3$ , $\aleph_4$ , ...(nagyság szerint növekvő sorrendben).

A végtelenek közötti különbségeket Cantor találta ki vagy fedezte fel... Hogy melyik szót használjuk, az is megérne egy misét.

Ismerve az ön rendkívüli képességeit - kedves A. úr - feltételezem, hogy magyarul is megtanult, ezért elmondom Erdős Pál, magyar matematikus bohókás költeményét:

Alef egy, alef kettő, alef három,

Georg Cantor a legnagyobb a világon.

Akhilleusz: Értem... Még ezt a kis csacska verset is. De őrizzük meg a komolyságunkat!

Teknős: Megpróbálom...

Közben a kihaltnak tűnő szálloda elé érnek. Még ott az irdatlan mennyiségű üres busz.

Akhilleusz: Szabad legyen egy egyszerű kérdést feltennem magának, kedves T. úr:

Hányan voltak éjszaka a szállodában?

Teknős: 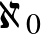$\aleph_0$ volt a létszám.

Akhilleusz: De mindenkinél ott volt a sorszám 1-től szinte 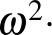$\omega^2\cdot$ 2-ig?!

Teknős: Igen. A pincér mesélte, hogy az 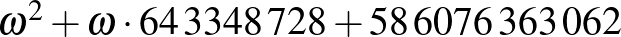$\omega^2+\omega\cdot 64\,3348\,728+58\,6076\,363\,062$ számú vendég, vagyis aki a második konvoj 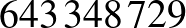$643\,348\,729$ -ik buszának 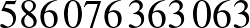$586\,076\,363\,063$ -ik ülésén utazva jött, a reggeli után panaszkodott: langyos volt neki a kakaó, ő forrón szereti.

Akhilleusz: Értem... Szerencse: kis cédulán rövid szám...

Teknős: Nem volt ilyen szerencsés egy másik vendéggel, aki lassúnak találta a felszolgálást - méltatlankodva még a panaszkönyvet is kérte. A végén a rendszámát is beleírta, de az sajnos olyan hosszú volt, hogy pár ezer lapot kitett.

Megkímélem a kedves Olvasót: nem írom ide a panaszkönyvből ezt a passzust.

Akhilleusz: Olyan nagy a panaszkönyv?

Teknős: Az igazgató – a korábbi tapasztalatokon okulva – egy végtelen számú lappal rendelkező panaszkönyvet rendszeresített.

A vendégeknek a recepción kiosztott cédulák is tetszőlegesen nagyok voltak, hogy bármekkora számokat írhassanak rájuk.

Akhilleusz: Aha...

Hoppá, eszembe jutott: Akár kisebb cédulákat, kisebb panaszkönyvet használhatnának, ha a betűk és a számjegyek végtelenül kicsik lennének, hiszen a végtelenül nagyító szemüveget már a béta-napon kitaláltuk.

Teknős: Ajánlhatnánk az igazgatónak. - Kevesebb papír: több élő fa. Éljen az erdő!...

Akhilleusz: Most hány vendég van a szállodában?

Teknős: Egy se. Reggeli után mindenki elutazott egy busszal.

A pincér ismerősöm így látta az étterem ablakából:

Mentek ki a szállodából az emberek. Sorban felszálltak az elsőként érkezett buszra.

A buszvezető is éppen olyan szigorú volt, mint a szálloda igazgatója: nagyon ügyelt az ültetési rendre. Mindenki a hotelban kapott szobaszáma szerinti ülésen foglalhatott helyet. Még üres helyek is maradtak. Ezután a busz elment. A többi buszra nem volt szükség.

Akhilleusz: Azért maradt itt ez a rengeteg busz? Megáll az ész!

Teknős: Furcsa, de így történt. Mondtam, hogy a létszámuk 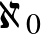$\aleph_0$ volt, tehát egy busznyian voltak.

Akhilleusz: Üres ülések is maradtak?

Teknős: Persze. Például az első szabad ülés a 200-as számú volt, mivel 3. buszkonvoj már nem jött, így az 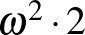$\omega^2\cdot 2$ sorszámot már nem osztották ki. A foglalt helyek ritkábban voltak.

Akhilleusz: Volt valaki, aki ugyanazon az ülésen utazott el, amelyiken jött?

Teknős: Jó kérdés. Hadd gondolkozzak... A 0 rendszámú biztosan. Az 1-től 9-ig rendszámúak is.

Azonban a 10-es rendszámú már nem, mivel a rendszáma: 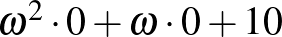$\omega^2\cdot 0+\omega\cdot 0+10$ , a három azonos hosszúságú szám: 00 és 00 és 10, összefésülve: 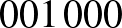$001\,000$ , vagyis a szobaszáma, és így az elmenő buszon az ülésszáma 1000 lett. (Az éjszaka első felében még a 100-as szobában volt.)

Akhilleusz: Vagyis tíz ilyen személy volt.

Teknős: Igen. Ők egyébként is nagyon szerencsések voltak: nyugodtan alhattak, az éjszaka nem kellett átköltözniük másik szobába.

Akhilleusz: Vajon megoldható, hogy senki se költözzék, ha új vendégek jönnek?

Teknős: Meg. Bár az igazgató most nem olyan módszert választott.

Akhilleusz: Az a módszer hogyan működne?

Teknős: Egyszerű. Példákat mutatok a szobaszámok kiutalására:

Ha a rendszám 0, akkor a szobaszám 1.

Ha 1, akkor a szobaszám 10.

Ha 5, akkor a szobaszám 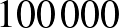$100\,000$ .

Ha 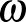$\omega$ , akkor a szobaszám 101.

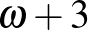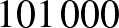Ha $\omega+3$ , akkor a szobaszám $101\,000$ .

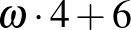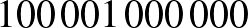Ha $\omega\cdot 4+6$ , akkor a szobaszám $100\,001\,000\,000$ .

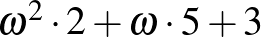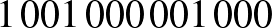Ha $\omega^2\cdot 2+\omega\cdot 5+3$ , akkor a szobaszám $1\,001\,000\,001\,000$ .

Akhilleusz: Látszik, hogy az 1-esek alkotják a hierarchia szintjei közötti határvonalakat, a limeszeket. a 0-k száma pedig megfelel a rendszám adott szintjében elfoglalt helyének...

De így nagyon ritkák lennének az elfoglalt szobák.

Teknős: Esetleg sűríthetnék őket, ha ezeket a szobaszámokat 2-es (bináris) számrendszerbeli számoknak tekintenék... De mindegy, a 10-es (decimális) számrendszerben is maradhatnak: tehát pl. a 101-es szobaszám öt helyett maradhat százegy... Nem számít, ha nagyon sok az üres szoba... Szobákban nem szűkölködnek...

Akhilleusz: Nagyon hosszúak lennének a szobaszámok. A példánkban szereplő 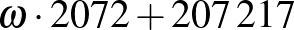$\omega\cdot 2072+207\,217$ sorszámú vendég szobaszámában 2 db 1-es és 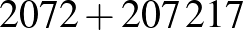$2072+207\,217$ db 0-s lenne.

Teknős: Az se számít, amúgy is hosszúak lennének... A 0-írásban különben is mi ketten nagyon jók vagyunk.

Akhilleusz: Viszont ebben a rendszerben nem zavarnak senkit az átköltöztetéssel, bármennyi új vendég jön is.

Teknős: Igaz, de az igazgató inkább a számjegy-összefésüléses módszert választotta... Talán, ha sokan panaszkodnak, áttér erre a módszerre...

És eddig még csak a megszámlálható végtelenekkel foglalkoztunk. A megszámlálhatatlan végtelenek még bizarrabbul viselkedhetnek.

Például, ha a Hilbert hotel fogadná a végtelen tér összes pontját:

Ahogy a mesében a szellem visszament a palackba, befolynának jól rendezetten – mivel Cantor tétele szerint minden halmazt jólrendezetté lehet tenni – egy vonalban a hotelba. A recepciósok csak néznének, és mivel nem tudják számlálni őket, nem adhatnak sorszámokat. Másnap eltávoznának egy rövid szakasz pontjaiként, és kiürülne a szálló, mivel ugyanannyi pont jött ki, mint ahány bement. Hát nem döbbenetes?!

Mit gondol, A. úr, ki bizonyította be, hogy a végtelen térnek – akár a több dimenziósnak is – ugyanannyi pontja van, mint egy rövid szakasznak?

Akhilleusz: Cantor.

Teknős: Ördöge van, A. úr!...

Akhilleusz: Maradjunk csak a megszámlálható végteleneknél! Térjünk vissza a rendszámokhoz!

Lépteimet számlálva futás közben elszámlálhatnék 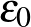$\varepsilon_0$ -ig?

Teknős: El...

De igencsak gyorsan kellene futnia, ha véges idő alatt akarná teljesíteni.

Akhilleusz: Úgy látom, eleinte csak kocognék, aztán egyre gyorsabban kellene futnom, limeszeken is áthaladva, hogy elérjem.

Teknős: Bizony. Gyorsulva kellene számlálnia a lépteit. És mivel az újabb fajta limeszek lépésszámban sokkal messzebb lennének, mint az előző fajtájúak voltak, még csak nem is egyenletesen gyorsulva kellene futnia, hanem hatványozottan. A sebessége már az első limeszszámnál (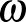 $\omega$ -nál) végtelen lenne. Ahogy Hilbert szállodájában is a személyzetnek egyre gyorsabb ütemben kellene dolgoznia, a vendégeknek is egyre gyorsabban kellene beköltözködniük.

Akhilleusz: Ha így elfutnék, mekkora lenne a távolságom magától?

Teknős: 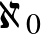$\aleph_0$ lépésnyi.

Akhilleusz: Végtelen sebesen futnék?... Ez nekem való!

De nem a fénysebesség a legnagyobb sebesség?

Teknős: Az a fizika világa.

Nehogy már a fizika gúzsba kössön minket! Mi most a matematika világában vagyunk. A kitalált legkisebb távolságunknál sem néztük, hogy hogyan mérhetnénk meg.

Henri Poincaré francia matematikus mondta: „A matematika a szellem szabad szárnyalása.”

Akhilleusz: Akkor nem csak rohanni, hanem szárnyalni is tudok... tudunk.

Teknős: Semmi és senki nem akadályozhat meg minket.

Akhilleusz: Csak papír és ceruza kell hozzá.

Teknős: (Magában: Még kütyü se. Hangosan:)

Meg ész... és kész.

Akhilleusz: Most búcsúzzunk el egymástól, kedves Teknős úr. Nagyon sokat tanultam magától.

Teknős: Viszont... Mindketten igyekeztünk, hogy – a matematika szigorát és szabatos kifejezéseit olykor talán áthágva – megértsük az érthetetlent. Azt hihetné rólam, hogy megértettem. Pedig...

Akhilleusz: Én is belekábultam... Valóság? ... Fikció? ...

Futni, kaszabolni egyszerűbb.

Teknős: Lehet... Csak vigyázzon a sarkára!

Viszontlátásra. kedves Akhilleusz úr.

Akhilleusz: Viszontlátásra, kedves Teknős úr.

Cammogva, száguldva el...

Keresztvölgyi József

Pécs, 2021. május