Az elmúlt néhány évtized technológiai fejlődése az „omic” (pl. genomic, azaz genomikus, stb.) adatok exponenciális növekedéséhez vezetett. Azonban arra, hogy ezekből az adathalmazokból megértsük az élet meghatározó törvényeit — ami matematikusok számára sosem látott lehetőségeket kínál — még várnunk kell. A biomolekuláris szerkezet és funkció közötti kapcsolat az élet egyik fő törvényszerűsége. E kapcsolatok leírása a kísértleti biológiában központi jelentőségű, a biofizikának pedig egyenesen a Szent Grálja.
A biomolekuláris szerkezet-funkció kapcsolatok megértéséhez elengedhetetlen a geometriai modellalkotás, amely hidat képez a biológiai adatok és az elméleti modellek, mint például kvantummechanika, molekuláris mechanika, statisztikus mechanika, termodinamika, illetve a többfázisú modellek között. A geometriaalapú modellek azonban legtöbbször túlságosan sok részletet vesznek figyelembe, emiatt nehezen használhatók konkrét számításokban.
A topológia juttat el a geometriai bonyolultság absztrakciójának legmagasabb szintjére, amikor a vizsgált terek komponenseinek csak az összefüggőségét vesszük figyelembe, és a tér független tartományait, gyűrűit és magasabb dimenziós lapjait topologikus invariánsaikkal (pl. Betti-számaikkal) írjuk le. Pontfelhőszerű adathalmazok (pl. atomok egy biomolekulában) topológiai invariánsainak tanulmányozásához az algebrai topológia különféle szimpliciális komplexusokat, például Vietoris—Rips-, Čech-, vagy alfa-komplexusokat hív segítségül. A 0-szimplexek pontok, az 1-szimplexek élek, a 2-szimplexek háromszögek, a 3-szimplexek tetraéderek, ahogy azt az 1. ábra is bemutatja. Az ezen szimpliciális komplexusokhoz hozzárendelt szimpliciális homológia segítségével adott adathalmazok Betti-számai szisztematikusan kiszámíthatók [7].
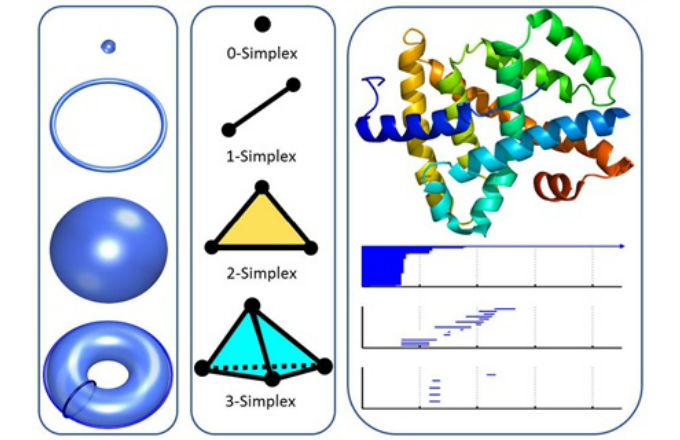
1. ábra: Topologikus invaránsok illusztrálása (balra), az alapvető szimplexek (középen), és egy fehérje perzisztencia-vonalkódja (jobbra). Balra: Fentről lefelé: egy pont, egy kör, egy üres gömb és egy tórusz. A nulladik, első és második Betti számok sorban: 1,0,0 a pontra, 1,1,0 a körre, 1,0,1 a gömbre és 1,2,1 a tóruszra. A tóruszra rajzolt két körvonal illusztrálja, hogy a második Betti szám 2. Középen: Négy tipikus szimplex. Jobbra: Egy fehérje (felül) és topologikus ujjlenyomata (alul). Képek: Zixuan Cang.
Mindazonáltal a hagyományos topológia és homológia teljesen mentes mindenféle távolságfogalomtól vagy koordinátáktól, így túl kevés információt hordoz ahhoz, hogy biomolekuláris vizsgálatokban hasznos legyen. A perzisztens homológia (más néven perzisztencia) — az algebrai topológia egy új ága — azonban többléptékű geometriai információt kódol a topologikus invariánsokba, létrehozva a geometria és a topológia szimbiózisát [14]. Egy paraméter — például golyók sugarának, vagy egy valós függvény szinthalmazainak — változtatásával ez az elmélet topologikus terek egy egész sorát (egy ún. filtrációt — a ford.) rendel hozzá egy adott objektumhoz. Következésképp a perzisztens homológia képes arra, hogy széles térbeli skálán ragadjon meg topológiai tulajdonságokat, amelyek rendszerint perzisztencia-vonalkódok [6], vagy perzisztencia-diagramok [5] segítségével ábrázolhatók. A skála változtatásával fellépő topologikus változásokat a vonalkód egyes vonalainak „születése”, „halála”, illetve „perzisztenciája” (azaz továbbélése, megmaradása) rögzíti. A perzisztens homológiát ezidáig számos tudományterületen alkalmazták, mint például a kép- és jelfeldolgozásban, a kaotikus dinamikában, szenzor-hálózatok és komplex rendszerek vizsgálatában, az alakfelismerésben, valamint a számítógépes biológiában is [13].
A nano- és biomolekulák esetében a perzisztens homológia kvantitatív topológiai analízist tesz lehetővé. Ily módon bizonyos biomolekuláris topologikus-funkcionális összefüggések felderíthetők pusztán az ún. „topologikus ujjlenyomat” (topological fingerprint) alapján [9,11]. Ez esetben — a közhiedelemmel ellentétben — a rövid életű topológiai jelenségek nem zajok, hanem a topologikus ujjlenyomat esszenciális részét képezik, ugyanis fontos szerepet játszanak fehérjék térszerkezeti stabilitásának és a fullerének görbületi energiájának kvantitatív topológiai analízisében [8,9]. Differenciálgeometria segítségével olyan parciális differenciálegyenleteken alapuló perzisztencia definiálható, amellyel biomolekulák vizsgálhatók [8]. A többdimenziós perzisztencia (multidimensional persistence) pedig különösen hasznosnak bizonyult a krio-elektronmikroszkópia általi szerkezet-meghatározás során felmerülő rosszul felállított inverz problémák megoldásában [10].
A topologikus ujjlenyomat biomolekuláknak olyan szisztematikus és egyedi reprezantációját adja, amelynek nincs hagyományos fizikai megfelelője. Szerencsére ez a reprezentáció könnyen elemezhető a gépi tanulás (machine learning), különösen a mély tanulás (deep learning) eszközkészletével, amely nemlineáris és magasabb rendű kölcsönhatásokat képes felismerni kellőképpen nagy és komplex adathalmazokban is. Az egyik első ilyen alkalmazás igencsak biztató: sikerült több tízezer olyan fehérjét osztályozni, amelyek együttesen több száz feladatot látnak el [4]. Hozzá kell tegyük, hogy a perzisztens homológia — miközben topológiailag egyszerűsíti a helyzetet — elhanyagol jónéhány kémiai és biológiai információt, így kvantitatív jóslatok esetében kevésbé versenyképes mint a geometriai vagy fizikaalapú reprezentációk. Ahhoz, hogy visszanyerjék a topologikus absztrakció során elveszett kémiai és biológiai információt, kutatók színezett biomolekula-hálózatokon alapuló elemspecifikus, vagy többkomponensű perzisztens homológiát vezettek be [2]. Ez a megközelítés biológiai tulajdonságokat — mint például hidrogénkötéseket, van der Waals-féle kölcsönhatásokat, hidrofilicitást és hidrofobicitást — topologikus invariánsokká konvertál, biomolekulák egy potenciálisan forradalmi reprezentációját adva [1,3].
A racionális gyógyszertervezés rendkívül fontos probléma az élettudományok terén, és egyúttal annak is tesztje, hogy mennyire értjük a biológiai rendszerek működését. Betegségeket gyógyító, valóban hatásos gyógyszerek fejlesztése a biológiai tudományok egyik legnagyobb kihívása. A többkomponensű perzisztens homológia kulcsfontosságú szerepet játszik a kötési „forrópontok” (binding hot-spots) előrejelzésében, a gyógyszerkötések pozíciójának analízisében, diszlokációs állandók megjóslásában, struktúraoptimalizálásban, a toxicitás elemzésében, valamint farmakokinetikus szimulációkban. Például a „D3R Grand Challenge” elnevezésű számítógéppel támogatott nemzetközi gyógyszertervezési versenyen egy gépi tanulást többskálajú súlyozott színezett gráfokkal és többkomponensű perzisztens homológiával összekapcsoló megoldás érte el a legjobb eredményt a Set 1 (Stage 2) adatsoron.
Irodalomjegyzék
- [1] Cang, Z.X., Wei, G.W. (2017): Analysis and prediction of protein folding energy changes upon mutation by element specific persistent homology. Bioinform., doi: 10.1093/bioinformatics/btx460.
- [2] Cang, Z.X., Wei, G.W. (2017): Integration of element specific persistent homology and machine learning for protein-ligand binding affinity prediction. Inter. J. Numer. Meth. Biomed. Eng., doi:10.1002/cnm.2914.
- [3] Cang, Z.X., Wei, G.W. (2017): TopologyNet: Topology based deep convolutional and multi-task neural networks for biomolecular property predictions. Plos Comp. Bio., 13(7), e1005690.
- [4] Cang, Z.X., Mu, L., Wu, K., Opron, K., Xia, K., Wei, G.W. (2015): A topological approach to protein classification. Mol. Based Math. Bio., 3, 140—162.
- [5] Edelsbrunner, H., Harer, J. (2008): Persistent homology — a survey. Cont. Math., 453, 257—282.
- [6] Ghrist, R. (2008): Barcodes: The persistent topology of data. Bull. Am. Math. Soc., 45, 61—75.
- [7] Kaczynski, T., Mischaikow, K., Mrozek, M. (2004): Computational Homology. In Applied Mathematical Sciences (Vol. 157). New York, NY: Springer-Verlag.
- [8] Wang, B., Wei, G.W. (2016): Object-oriented persistent homology. J. Comp. Phys. 305, 276—299.
- [9] Xia, K.L., Wei, G.W. (2014): Persistent homology analysis of protein structure, flexibility and folding. Inter. J. Num. Meth. Biomed. Eng., 30, 814—844.
- [10] Xia, K.L., Wei, G.W. (2015): Persistent topology for cryo-EM data analysis. Inter. J. Num. Meth. Biomed. Eng., 31, e02719.
- [11] Xia, K.L., Feng, X., Tong, Y.Y., Wei, G.W. (2015): Persistent homology for the quantitative prediction of fullerene stability. J. Comp. Chem., 36, 408—422.
- [12] Xia, K.L., Zhao, Z.X., Wei, G.W. (2015): Multiresolution topological simplification. J. Comp. Bio., 22, 1—5.
- [13] Yao, Y., Sun, J., Huang, X.H., Bowman, G.R., Singh, G., Lesnick, M., Carlsson, G. (2009): Topological methods for exploring low-density states in biomolecular folding pathways. J. Chem. Phys., 130, 144115.
- [14] Zomorodian, A., Carlsson, G. (2005): Computing persistent homology. Dis. Comp. Geo., 33, 249—274.
A cikk eredetileg a SIAM News 2017 decemberi számában jelent meg Persistent Homology Analysis of Biomolecular Data címmel; a fordítás Huszár Kristóf és Stipsicz András munkája.
Guo-Wei Wei
Michigan State University









