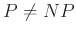Mozdonyhozzárendelés a vasúti teherszállításban

Bevezetés

Egy jól működő cég számára a rendelkezésre álló erőforrások optimális felhasználása kulcsfontosságú. A MÁV-TRAKCIÓ Zrt. (2014 óta a MÁV-START része) is ezért kereste meg a BME Matematika Intézetének Illés Tibor vezette Optimalizálási Csoportját. A vállalat vasúti vontatási feladatok ellátásával foglalkozik, vagyis megállapodik egy ügyféllel, hogy az ügyfél vasúti kocsikra pakolt szállítmányát egy adott helyen és időben felveszi, majd a saját mozdonyai segíségével elszállítja egy másik adott helyre és időre.

A cég erőforrásai tehát a mozdonyok, illetve az általuk felhasznált üzemanyag. Ideális esetben egy vontatás elvégzéséhez nem az ország másik oldaláról szeretnének mozdonyt küldeni, hanem a közelből; tökéletes esetben egy mozdony pont azon az állomáson fejezett be egy korábbi vontatást, ahol egy újabb feladat várja. Az elvállalt megbízások ismeretében tehát egy olyan tehervonat menetrendet szeretnénk készíteni, ami minimalizálja a mozdonyok által megtett távolságot.¹

A projekt előtt a vállalat ezt úgy oldotta meg, hogy az országot három régióra osztotta, és mindegyiket egy tapasztalt diszpécser irányította, gyakorlatilag kézzel készítve a mozdonyfordulókat — az időnként — változó tehervonat menetrendre. Ez a működési forma a megbízások számának növekedésével egyre inkább tarthatatlanná vált. Természetesen a projekt után is szükség van emberi felügyeletre, de a mozdonyfordulók automatizált tervezése teher menetrend esetén is lehetségessé vált, megkönnyítve a diszpécserek munkáját. Az optimalizált mozdonyfordulók a mozdonyok hatékonyabb kihasználásával csökkentik a tehervonat vontatási költségeit, a késéseket, és nem utolsósorban a károsanyag-kibocsátást.

A fénykép forrása: http://iho.hu/hir/halasi-hatos (Kovács Kitti fotója)

A matematikai modell

Legyen a teljesítendő megbízások (tehervonatok) halmaza $V$ . Minden $v \in V$ megbízáshoz rendelkezésünkre állnak a következő adatok: indulási hely, indulási idő, érkezési hely, érkezési idő, útvonal, használható mozdonytípusok. A felépített matematikai modell egy hálózati folyam, melyben minden $v$ megbízásnak megfelel egy $v'$ és $v''$ csúcs, illetve egy $(v',v'')$ él. Ha egy mozdony a $v$ megbízás teljesítése után képes elvégezni a $w$ megbízást, akkor felveszünk egy $(v'', w')$ élt. Ez akkor teljesül, ha a $v$ elvégzése után van elég idő az esetleges gépmenetre $v$ érkezési helyéről $w$ indulási helyére, illetve a szerelvények összerakására, ellenőrzésre („technikai idő”):

érkezési idő $\displaystyle _{v}+$ gépmenet $\displaystyle ($ érkezési hely $\displaystyle _{v},$ indulási hely $\displaystyle _{w})+$ technikai idő $\displaystyle \leq$ indulási idő $\displaystyle _{w}$

Bevezetünk továbbá egy $s$ forrást és $t$ nyelőt, és felveszünk minden $v$ -re egy $(s,v')$ és $(v'',t)$ élt. Végül bevezetünk egy $(t,s)$ élt. Az így kapott hálózati folyamot szemlélteti az 1. ábra.

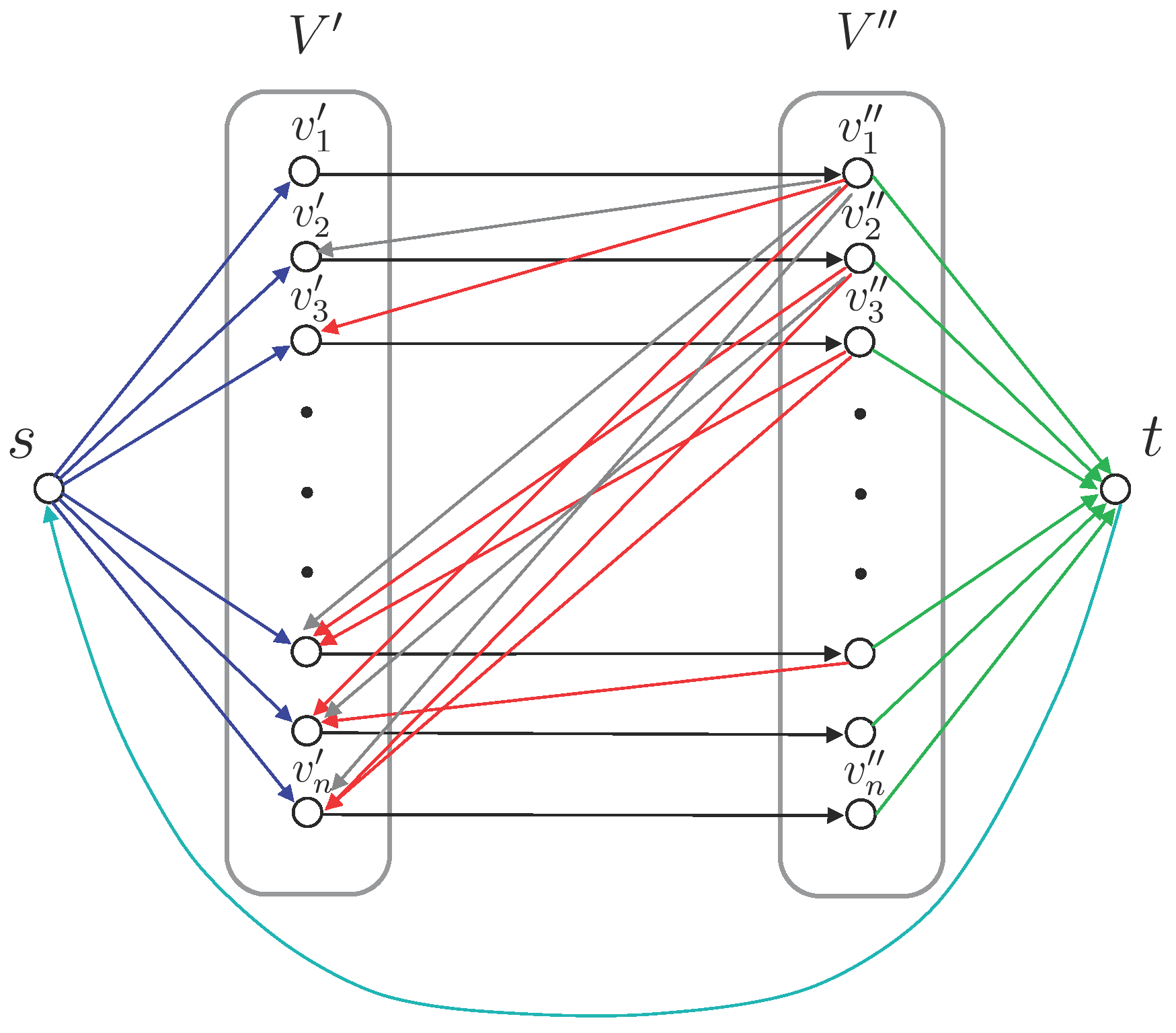
1. ábra. Minimális költségű hálózati folyammodell

Látható, hogy egy $1$ értékű $s$ -ből $t$ -be menő folyam megfeleltethető egy úgynevezett mozdonyfordulónak (egy mozdony által elvégzett feladatsorozat). Megkövetelve, hogy mindegyik $(v',v'')$ típusú élen legalább $1$ legyen a folyamérték, a modell megengedett megoldásai leírják a valós feladat megoldásait.

Mi legyen a feladat célfüggvénye? Ez gyakorlati feladatoknál nem mindig egyértelmű. A $(t,s)$ élen levő folyamérték megegyezik az elvégzendő megbízások elvégzéséhez felhasznált mozdonyok számával, így tudjuk ezt is minimalizálni. Illetve a gépmeneteknek² megfelelő élek célfüggvény-együtthatóját a megtett távolságra állítva tudjuk az összes gépmenetet is minimalizálni. A két célfüggvény megfelelő súlyozásával (lineáris kombinációjával), a gyakorlatban is jól használható — optimális — megoldások állíthatók elő.³

Implementáció és eredmények

Egy jellemző méretű feladat a havi terv. Mivel a személyzetnek 15 nappal a hónap kezdete előtt meg kell adni egy munkabeosztástervet, így a következő hónap tervét a jelenlegi hónap közepén rendelkezésre álló adatok alapján kell optimalizálni. Ez persze szükségessé tesz későbbi változtatásokat, de a módszer hatékonyságát jól méri.

Egyik implementációnk egy C++ kód volt, melyben csak a felhasznált mozdonyok számát minimalizáltuk. Mivel itt nemnulla célfüggvény-együtthatója csak a $(t,s)$ élnek van, így lényegében egy maximális folyamfeladatról van szó. A havi terv mozdonytípusok szerint három feladattá lett szétbontva, ezeken a futási eredmények a következők voltak (Intel Core i7-3630QM processzoron):

Mozdonytípus	0431	0628	0630
Tehervonatok száma	3068	1458	2020
Gráf mérete	825 099 él	185 221 él	366 513 él
Optimum	34 mozdony	19 mozdony	25 mozdony
Futásidő	9 p 11 mp	45 mp	2 p 17 mp

Az így kapott megoldásokról elmondható, hogy viszonylag egyenletesen terhelik a mozdonyokat. Például a 0431-es típusú mozdonyok mindegyike 138 és 180 közötti megbízást végez el az adott hónapban, a 34 mozdony⁴ közül 23 pedig 151 és 164 közöttit.

Másfelől a gépmenetek hossza nincs figyelembevéve a modellben, így nem meglepő, hogy a mozdonyfordulók elég pazarlók. Ismét a 0421-es típusú mozdonyokat tekintve, összességében a mozdonyok az összesen megtett távolság $35{,}3\%$ -át gépmenetként végzik.

A feleslegesen megtett távolság csökkentése érdekében a maximális folyamfeladat helyett minimál költséges folyamfeladatot fogalmaztunk meg. Ennek a modellnek a megoldására — a feladat mérete miatt — már optimalizálási feladatok megoldására specializált szoftvert használtunk: a matematikai modelleket Mosel modellezési nyelven fogalmaztuk meg, és az XPRESS-MP programcsomaggal oldottuk meg. Sikerült olyan megoldást találnunk, amelynél azonos mozdonyszám mellett a felesleges gépmenetek össztávolsága lényegesen leszoríthatóak (például a 0431-esek gépmenetaránya $11{,}2\%$ -ra csökkent), míg a számítás futásideje nagyságrendileg megegyező maradt.⁵

Összefoglalás, további kutatási irányok

A felhasznált módszerek, számítási eredményeink meggyőzték a MÁV-TRAKCIÓ Zrt. munkatársait a (klasszikus) operációkutatási modellek és megoldási módszerek hasznosságáról, alkalmazhatóságáról középtávú tervezési feladatok megoldására.

A gyakorlatban a tehervonat-megrendelések eléggé kaotikus képet mutatnak, azaz a tervek elkészítésének időpontjában (15 nappal a modellezett hónap előtt) a valóságban közlekedő vonatok mindösszesen 65%-a ismert. Sőt a tervezett tehervonatok és a leközlekedett tehervonatok az indulást megelőző 3. napon is több, mint 20%-os eltérést mutatnak. Ez szükségessé tette a mozdonyfordulók újraütemezését. A bevezetett modellek már közel sem voltak klasszikus operációkutatási feladatnak tekinthetők, sőt a szakirodalom áttekintése után bebizonyosodott, hogy ezen a területen az újraütemezési modelljeink az operációkutatási szakirodalomban újak. Az újraütemezési feladatoknál az alapelvárás az volt, hogy a tervekhez képest minimális legyen a módosítás, vagy másképpen megfogalmazva, azok a tehervonatok, amelyek egy mozdonyfordulóba kerültek, lehetőleg maradjanak egy mozdonyfordulóban. Ennek az az értelme, hogy a mozdonyfordulók kialakítása után tervezik meg a személyzet hozzárendelését a tehervonatokhoz, vagyis ha a mozdonyfordulók jelentősen változnak, akkor a személyzet-hozzárendelést is módosítani kell.

A fénykép forrása: https://www.flickr.com/photos/gadam91/4457712466/in/gallery-41517609@N05-72157656244807942/ (Garamvölgyi Ádám fotója)

Az újraütemezési feladat már egy bonyolultabb operációkutatási problémára, a többtermékes hálózati folyamfeladatra vezetett, amelynek megoldására valószínűleg nem létezik polinomiális algoritmus.⁶ Természetes következménye a többtermékes hálózati folyamfeladatra ismertetett bonyolultságelméleti eredménynek az, hogy az újraütemezési feladatok futási ideje még akkor is jelentősen megnövekedett, ha az újraütemezés időhorizontját egy hónap helyett egy hétre csökkentettük le. Találtunk olyan tesztfeladatot, amelynek a megoldása több órát vett igénybe. Ha azonban az újraütemezést csak három napra kívánjuk elvégezni, akkor az általunk vizsgált esetekben az XPRESS-MP futási ideje nem haladta meg az egy órát.

Az újraütemezési feladat jobb megismerése, politópjának vizsgálata, hatékony vágások előállítása még sok kutatási feladatot ad az operációkutatóknak. A gyakorlati feladatok gyorsabb megoldása érdekében hatékony approximációs algoritmusok, vagy a feladat tulajdonságait kihasználó heurisztikus módszerek kidolgozása szükséges.

Irodalomjegyzék

[1] Barta Zs.: Vasút optimalizálási problémák: matematikai módszerek és modellek. MSc diplomamunka, Budapesti Műszaki és Gazdaságtudományi Egyetem, 2011.

[2] Illés T, Makai M, Vaik Zs.: Combinatorial Optimization Model for Railway Engine Assignment Problem. In: Kroon L G, Möhring R H (editors) Proceedings of the 5th Workshop on Algorithmic Methods and Models for Optimization of Railways.Dagstuhl: Internationales Begegnungs- und Forschungszentrum für Informatik (IBFI), 2006. ISBN: 978-3-939897-00-2.

[3] Illés T.: Optimization models for railway freight transportation. 26th European Conference on Operational Research, 2013, Róma.

[4] Illés T, Molnár-Szipai R.: Strongly polynomial primal monotonic build-up simplex algorithm for maximal flow problems. Discrete Applied Mathematics 214, 2016.

[5] Molnár-Szipai R.: Hatékony pivot algoritmusok hálózati folyamfeladatokra. MSc diplomamunka, Budapesti Műszaki és Gazdaságtudományi Egyetem, 2012.

Illés Tibor, Molnár-Szipai Richárd,

BME Matematika Intézet

Lábjegyzetek

¹: Természetesen más ésszerű célt is megfogalmazhatnánk, például a vontatás összköltségének a minimalizálását, amelyben a szükséges mozdonyok által befutott távolság csak az egyik összetevője az összköltségnek.
²: Gépmenetnek nevezzük a mozdonyok vontatás nélküli közlekedtetését, abból a célból, hogy egyik állomásról átkerüljön egy másikra, ahol elvégzendő megbízás várja.
³: Itt kell megjegyeznünk, hogy a feladat — matematikai — természetéből adódóan, létezhetnek un. alternatív optimális megoldások, amelyek azonos célfüggvényérték mellett, strukturálisan különböző megoldást eredményeznek, azaz a gyakorlati felhasználás szempontjából különbözhetnek.
⁴: A feladatok megoldásában jelentkező szükséges mozdonyszám egyben a mozdonyfordulók számát is jelenti.
⁵: A maximális folyam, illetve a minimál költséges folyam feladatok megoldására ismertek polinomiális algoritmusok, amelyek a gyakorlatban is hatékonyak.
⁶: Az algoritmusok hatékonyságával, illetve a matematikai/számítástudományi/optimalizálási problémák bonyolultságával, komplexitásával foglalkozó területe a matematikának a bonyolultságelmélet, amelyiknek egyik eredménye az említett állítás, azaz a többtermékes hálózati folyamfeladat megoldására nem létezhet polinomiális algoritmus, ha $P \neq NP$