A nagyméretű gráfok mindenütt jelen vannak a matematikában, és a szerkezetük leírása a modern kombinatorika egyik fontos célja. A leghíresebb leírást a Szemerédi-féle regularitási lemma (1978) adja meg, amely azt állítja, hogy bármely kellően nagyméretű gráf csúcsai feloszthatók nagyjából azonos méretű halmazokra úgy, hogy az élek a halmazok többsége között jó közelítéssel véletlenszerűnek tűnnek.
A nagy véges objektumok tanulmányozásának egyik módja az, hogy az egyre nagyobb és nagyobb objektumok sorozatai helyett áttérünk ideális limeszobjektumokra. Ha megfelelően járunk el, a limeszobjektumok tulajdonságai tükrözik az őket közelítő véges objektumok tulajdonságait, és fordítva.
A grafonok a nagy véges gráfok sorozataihoz tartozó limeszobjektumok az úgynevezett vágásmetrikára nézve. Angol nevét (graphon) a gráf (graph) és függvény (function) szavak összevonásával alkották.
A fogalmat Borgs, Chayes, Lovász, T. Sós, Szegedy és Vesztergombi vezette be és dolgozta ki [1,3]. A grafonok természetes módon bukkannak fel olyan területeken, ahol nagy gráfok sorozatai fordulnak elő: extremális gráfelmélet, nagy gráfok tulajdonságtesztelése, kvázi-véletlen gráfok, véletlen hálózatok, statisztikus fizikai rendszerek termodinamikai limeszei, és így tovább.
Kezdjük néhány definícióval és motivációként egy példával. Egy 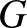 gráf alatt csúcsoknak egy
gráf alatt csúcsoknak egy 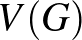 halmazát és éleknek egy
halmazát és éleknek egy 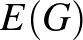 halmazát értjük, utóbbinak az elemei különböző csúcsokból alkotott párok. Egy gráfhomomorfizmus
halmazát értjük, utóbbinak az elemei különböző csúcsokból alkotott párok. Egy gráfhomomorfizmus 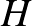 -ból
-ból 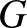 -be egy olyan
-be egy olyan 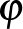 leképezés
leképezés  -ból
-ból 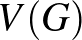 -be, amely megőrzi az élek menti szomszédságot. Azaz minden
-be, amely megőrzi az élek menti szomszédságot. Azaz minden 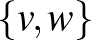 élre
élre 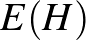 -ból a
-ból a 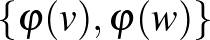 egy él
egy él 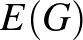 -ben. Jelöljük
-ben. Jelöljük 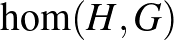 -vel a homomorfizmusok számát
-vel a homomorfizmusok számát 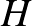 -ból
-ból 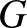 -be. Például
-be. Például 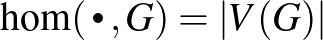 ,
, 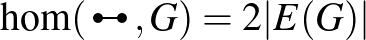 és
és 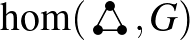 a
a 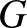 -ben lévő háromszögek számának 6-szorosa.
-ben lévő háromszögek számának 6-szorosa.
A lehetséges leképezések számával normalizálva kapjuk a  homomorfizmus-sűrűségét
homomorfizmus-sűrűségét 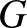 -ben,
-ben,
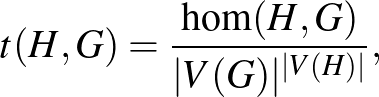
ami annak a valószínűsége, hogy egy véletlenszerűen választott leképezés  -ból
-ból 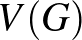 -be megőrzi az élek menti szomszédságot. Ez a szám egyben a
-be megőrzi az élek menti szomszédságot. Ez a szám egyben a 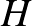 mint részgráf sűrűségét is méri
mint részgráf sűrűségét is méri 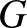 -ben, aszimptotikusan, ahogy
-ben, aszimptotikusan, ahogy  . Például
. Például 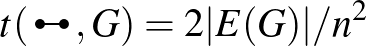 , míg a
, míg a  -ben lévő élek sűrűsége
-ben lévő élek sűrűsége 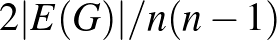 . Ez a a két kifejezés nagy
. Ez a a két kifejezés nagy 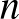 -re közel azonos.
-re közel azonos.
Tekintsük a következő extremális gráfelméleti problémát: Hány 4 hosszú körnek kell lennie egy olyan gráfban, amelynek élsűrűsége legalább 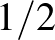 ? Könnyű belátni, hogy bármely
? Könnyű belátni, hogy bármely 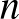 csúcsú gráfban a 4 hosszú körök száma nagyságrendileg legfeljebb
csúcsú gráfban a 4 hosszú körök száma nagyságrendileg legfeljebb 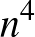 . Erdős egyik tétele szerint a lehetséges élek legalább felét tartalmazó gráfokban a 4 hosszú körök száma nagyságrendileg legalább
. Erdős egyik tétele szerint a lehetséges élek legalább felét tartalmazó gráfokban a 4 hosszú körök száma nagyságrendileg legalább 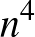 . Pontosabban, bármely
. Pontosabban, bármely 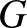 gráfra
gráfra
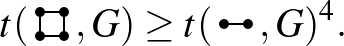
Speciálisan, ha 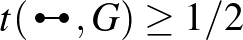 , akkor
, akkor 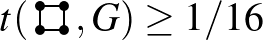 . Ennek fényében a probléma újrafogalmazható minimalizálási problémaként: minimalizáljuk
. Ennek fényében a probléma újrafogalmazható minimalizálási problémaként: minimalizáljuk 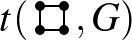 -t olyan véges
-t olyan véges  gráfokon, amelyek kielégítik
gráfokon, amelyek kielégítik 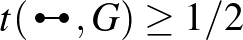 -et. Némi munkával megmutatható, hogy nincs olyan véges
-et. Némi munkával megmutatható, hogy nincs olyan véges 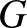 gráf, amelyre
gráf, amelyre 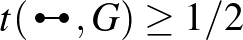 , és melyre
, és melyre  eléri az
eléri az 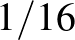 -ot.
-ot.
Ezen a ponton érdemes párhuzamot vonnunk egy elemi analízis problémával: minimalizáljuk 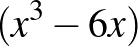 -et az
-et az 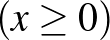 -t kielégítő racionális számok között. Ennek a polinomnak
-t kielégítő racionális számok között. Ennek a polinomnak 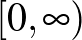 -en globális minimuma van
-en globális minimuma van 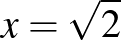 -nél, így a legjobb, amit a racionális számok körében tehetünk az, hogy megmutatjuk, hogy a polinom a minimumhoz közelítő értékeket vesz fel racionális számok egy
-nél, így a legjobb, amit a racionális számok körében tehetünk az, hogy megmutatjuk, hogy a polinom a minimumhoz közelítő értékeket vesz fel racionális számok egy  -höz tartó sorozata mentén. Jól tudjuk, hogy ezt a bonyodalmat úgy kell elkerülni, hogy a racionális számokat (mint metrikus teret) teljessé tesszük, kiegészítjük a valós számokkal, és egy ilyen sorozat határértékét
-höz tartó sorozata mentén. Jól tudjuk, hogy ezt a bonyodalmat úgy kell elkerülni, hogy a racionális számokat (mint metrikus teret) teljessé tesszük, kiegészítjük a valós számokkal, és egy ilyen sorozat határértékét  -vel realizáljuk.
-vel realizáljuk.
Van olyan véges gráfokból álló sorozat, amelyben az élsűrűség legalább 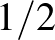 és a 4 hosszú körök sűrűsége megközelíti az
és a 4 hosszú körök sűrűsége megközelíti az 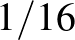 -ot. Legyen
-ot. Legyen 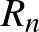 egy
egy 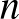 csúcsú véletlen gráf, ahol minden él beválasztása függetlenül,
csúcsú véletlen gráf, ahol minden él beválasztása függetlenül, 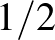 valószínűséggel dől el. Elhagyva azokat az
valószínűséggel dől el. Elhagyva azokat az 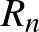 -eket amelyekben
-eket amelyekben 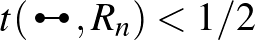 , egy olyan gráfsorozatot kapunk, amiben a 4 hosszú körök sűrűsége 1 valószínűséggel konvergál
, egy olyan gráfsorozatot kapunk, amiben a 4 hosszú körök sűrűsége 1 valószínűséggel konvergál 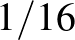 -hoz. Követve a
-hoz. Követve a  analógiáját, érdemes megpróbálnunk realizálni ennek a véges gráfsorozatnak a limeszét, és megérteni, hogyan oldja meg az adott minimalizálási problémát.
analógiáját, érdemes megpróbálnunk realizálni ennek a véges gráfsorozatnak a limeszét, és megérteni, hogyan oldja meg az adott minimalizálási problémát.
Mi lehet ennek az  véletlen gráfsorozatnak a limesze? Egy címkézett gráf szomszédsági mátrixából konstruáljuk meg a gráf pixelképét úgy, hogy az 1-eseket fekete négyzetekké alakítjuk, a 0-ákat pedig fehérekké, és a
véletlen gráfsorozatnak a limesze? Egy címkézett gráf szomszédsági mátrixából konstruáljuk meg a gráf pixelképét úgy, hogy az 1-eseket fekete négyzetekké alakítjuk, a 0-ákat pedig fehérekké, és a ![$[0,1]^2$](/images/stories/latexuj/2024-11/2024-11-miisazagrafon/img34.png) egységnégyzetre skálázunk:
egységnégyzetre skálázunk:
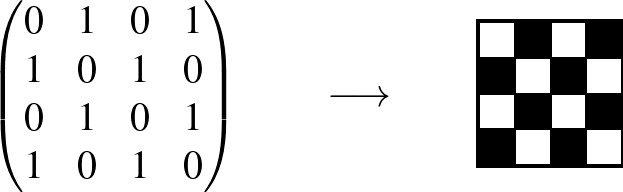
A pixelképeken látható, hogy grafikusan „konvergálnak”: az egyre nagyobb és nagyobb  élvalószínűségű véletlen gráfok (bármilyen címkézéssel) egy szürke négyzethez konvergálnak, a konstans
élvalószínűségű véletlen gráfok (bármilyen címkézéssel) egy szürke négyzethez konvergálnak, a konstans  függvényhez
függvényhez ![$[0,1]^2$](/images/stories/latexuj/2024-11/2024-11-miisazagrafon/img34.png) -en.
-en.

A konstans 1/2 függvény a ![$[0,1]^2$](/images/stories/latexuj/2024-11/2024-11-miisazagrafon/img34.png) -en egy példa címkézett grafonra. A címkézett grafon egy szimmetrikus, Lebesgue-mérhető függvény
-en egy példa címkézett grafonra. A címkézett grafon egy szimmetrikus, Lebesgue-mérhető függvény ![$[0,1]^2$](/images/stories/latexuj/2024-11/2024-11-miisazagrafon/img34.png) -ből
-ből ![$[0,1]$](/images/stories/latexuj/2024-11/2024-11-miisazagrafon/img36.png) -be (a szokásos, nullmértékű eltérés esetén azonosítással). Az ilyen függvényekre tekinthetünk a
-be (a szokásos, nullmértékű eltérés esetén azonosítással). Az ilyen függvényekre tekinthetünk a ![$[0,1]$](/images/stories/latexuj/2024-11/2024-11-miisazagrafon/img36.png) csúcshalmazon vett élsúlyozott gráfokként. A címkézetlen grafon egy átcímkézés erejéig megadott grafon, ahol átcímkézés alatt a
csúcshalmazon vett élsúlyozott gráfokként. A címkézetlen grafon egy átcímkézés erejéig megadott grafon, ahol átcímkézés alatt a ![$[0,1]$](/images/stories/latexuj/2024-11/2024-11-miisazagrafon/img36.png) intervallum egy invertálható és mértéktartó transzformációjának végrehajtását értjük. Vegyük észre, hogy bármely pixelkép egy címkézett grafon, vagyis a (címkézett) gráfok egyben (címkézett) grafonok.
intervallum egy invertálható és mértéktartó transzformációjának végrehajtását értjük. Vegyük észre, hogy bármely pixelkép egy címkézett grafon, vagyis a (címkézett) gráfok egyben (címkézett) grafonok.
Ennek a konvergenciának egy másik példájaként tekintsük a növekvő egyenletes kapcsolódási gráfok  sorozatát, amelyet induktív módon a következőképpen definiálunk. Legyen
sorozatát, amelyet induktív módon a következőképpen definiálunk. Legyen 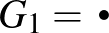 , és
, és 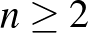 esetén konstruáljuk
esetén konstruáljuk 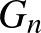 -t a
-t a 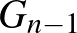 -ből úgy, hogy hozzáadunk egy új csúcsot, majd minden egyes élt, amely még nem szerepel
-ből úgy, hogy hozzáadunk egy új csúcsot, majd minden egyes élt, amely még nem szerepel 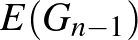 -ben, egymástól függetlenül
-ben, egymástól függetlenül 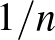 valószínűséggel beveszünk. Kiderül, hogy ez a gráfsorozat 1 valószínűséggel konvergál az
valószínűséggel beveszünk. Kiderül, hogy ez a gráfsorozat 1 valószínűséggel konvergál az 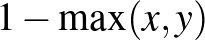 grafonhoz. (Mivel a mátrixok indexelésénél a
grafonhoz. (Mivel a mátrixok indexelésénél a  a bal felső sarok, így a grafonoknál is).
a bal felső sarok, így a grafonoknál is).

A teljes páros gráfok címkézésének két természetes módja is van, és ezek a teljes páros gráfok sorozatának különböző limeszgrafonjaira utalnak. Valójában mindkét címkézett grafonsorozatnak ugyanaz a limesze, amint az ábra is mutatja. Arra biztatjuk az olvasót, hogy térjen vissza ehhez a példához, miután a konvergenciát pontosabban definiáltuk.

A homomorfizmus-sűrűségek természetes módon kiterjednek grafonokra is. Egy véges 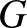 gráf esetén a
gráf esetén a 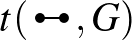 sűrűség kiszámítható úgy, hogy a
sűrűség kiszámítható úgy, hogy a 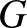 minden egyes csúcsának adunk
minden egyes csúcsának adunk 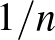 tömeget, és a csúcspárokon integráljuk az élek indikátorfüggvényét. Pontosan ugyanígy, egy
tömeget, és a csúcspárokon integráljuk az élek indikátorfüggvényét. Pontosan ugyanígy, egy 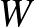 címkézett grafon
címkézett grafon 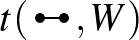 élsűrűsége
élsűrűsége
![$\displaystyle \int_{[0,1]^2} W(x,y)\,dxdy,
$](/images/stories/latexuj/2024-11/2024-11-miisazagrafon/img48.png)
és a 4 hosszú körök 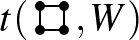 sűrűsége
sűrűsége
![$\displaystyle \int_{[0,1]^4} W(x_1,x_2)W(x_2,x_3)W(x_3,x_4)W(x_4,x_1)\, dx_1 dx_2 dx_3 dx_4.
$](/images/stories/latexuj/2024-11/2024-11-miisazagrafon/img50.png)
Innen már egyszerű egy 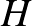 véges gráfnak a
véges gráfnak a 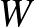 grafonban vett
grafonban vett  homomorfizmus-sűrűségére felírni a megfelelő kifejezést. A felírt formulák alapján látjuk, hogy a
homomorfizmus-sűrűségére felírni a megfelelő kifejezést. A felírt formulák alapján látjuk, hogy a 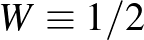 konstans grafon megoldja a minimalizálási problémát:
konstans grafon megoldja a minimalizálási problémát: 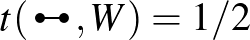 , míg
, míg  .
.
Azért, hogy a véges gráfok terének teljessé tételével megkapjuk a grafonok terét, és hogy a grafonok konvergenciáját precízen definiálhassuk, bevezetjük a 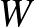 és
és 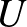 címkézett grafonok
címkézett grafonok  vágástávolságát:
vágástávolságát:
ahol az infimumot a  és
és  összes
összes 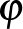 és
és 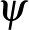 átcímkézése felett vesszük, a szuprémumot pedig a
átcímkézése felett vesszük, a szuprémumot pedig a ![$[0,1]$](/images/stories/latexuj/2024-11/2024-11-miisazagrafon/img36.png) összes mérhető
összes mérhető  és
és 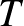 részhalmazán. A vágástávolság először a maximális eltérést méri két felcímkézett grafon integráljai között
részhalmazán. A vágástávolság először a maximális eltérést méri két felcímkézett grafon integráljai között ![$[0,1]^2$](/images/stories/latexuj/2024-11/2024-11-miisazagrafon/img34.png) mérhető szorzathalmazain (innen a
mérhető szorzathalmazain (innen a  jelölés), majd minimalizálja ezt a maximális eltérést az összes lehetséges átcímkézés felett. (Két véges gráf vágástávolságát kombinatorikusan is definiálhatjuk, bárminemű analízis nélkül, de a definíció meglehetősen komplikált.)
jelölés), majd minimalizálja ezt a maximális eltérést az összes lehetséges átcímkézés felett. (Két véges gráf vágástávolságát kombinatorikusan is definiálhatjuk, bárminemű analízis nélkül, de a definíció meglehetősen komplikált.)
A vágástávolságot a definícióban szereplő infimum jól definiálttá teszi a címkézetlen grafonok terén, de még nem válik metrikává. Az olyan 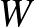 és
és 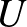 grafonokat, amelyekre
grafonokat, amelyekre 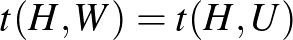 minden véges
minden véges 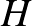 gráfra, gyengén izomorfnak nevezzük. Kiderül, hogy
gráfra, gyengén izomorfnak nevezzük. Kiderül, hogy 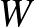 és
és 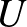 akkor és csak akkor gyengén izomorf, ha
akkor és csak akkor gyengén izomorf, ha  . A vágástávolság ténylegesen metrikává válik a címkézetlen grafonok
. A vágástávolság ténylegesen metrikává válik a címkézetlen grafonok 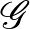 terén, ha azokat gyenge izomorfizmus erejéig tekintjük. A pixelképek konvergenciájának imént bemutatott példáit tekinthetjük konvergens sorozatoknak és azok határértékeinek
terén, ha azokat gyenge izomorfizmus erejéig tekintjük. A pixelképek konvergenciájának imént bemutatott példáit tekinthetjük konvergens sorozatoknak és azok határértékeinek 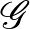 -ben (gyenge izomorfizmus erejéig).
-ben (gyenge izomorfizmus erejéig).
Végezetül kiemelünk néhány alapvető eredményt a grafonokkal kapcsolatban. Az oldalhivatkozások Lovász könyvéből [2] származnak, amit bátran ajánlunk a további részletek után érdeklődő olvasó figyelmébe.
1. tétel. (Prop. 11.32, 185. oldal) Minden grafon véges gráfok egy sorozatának 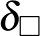 -limesze.
-limesze.
Egy 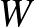 címkézett grafon egy véges címkézett gráffal való közelítéséhez legyen
címkézett grafon egy véges címkézett gráffal való közelítéséhez legyen  egy
egy ![$[0,1]$](/images/stories/latexuj/2024-11/2024-11-miisazagrafon/img36.png) -ből véletlenszerűen kiválasztott,
-ből véletlenszerűen kiválasztott, 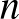 pontból álló halmaz, majd konstruáljunk egy olyan gráfot
pontból álló halmaz, majd konstruáljunk egy olyan gráfot  -en, amelyben a
-en, amelyben a 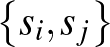 él
él 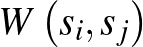 valószínűséggel szerepel. Ez a címkézett gráf vágástávolságban nagy valószínűséggel jól közelíti
valószínűséggel szerepel. Ez a címkézett gráf vágástávolságban nagy valószínűséggel jól közelíti 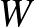 -t (ahogy
-t (ahogy  ).
).
2. tétel. (Thm. 9.23, 149. o.) A 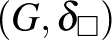 tér kompakt.
tér kompakt.
Ebből következik, hogy 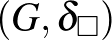 egy teljes metrikus tér. Ezt a tényt az 1. tétellel kombinálva azt látjuk, hogy a grafonok tere a véges gráfok terének a teljessé tétele a vágásmetrikára! Ez a tétel azt is mutatja, hogy a grafonok hogyan képeznek hidat Szemerédi regularitási lemmájának különböző alakjai között: a 2. tétel levezethető a lemma egy gyenge formájából, míg egy erősebb regularitási lemma a
egy teljes metrikus tér. Ezt a tényt az 1. tétellel kombinálva azt látjuk, hogy a grafonok tere a véges gráfok terének a teljessé tétele a vágásmetrikára! Ez a tétel azt is mutatja, hogy a grafonok hogyan képeznek hidat Szemerédi regularitási lemmájának különböző alakjai között: a 2. tétel levezethető a lemma egy gyenge formájából, míg egy erősebb regularitási lemma a 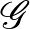 kompaktságából következik.
kompaktságából következik.
3. tétel. (Lem. 10.23, 167. o.) Minden 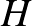 véges gráfra a
véges gráfra a ![$t(H, \cdot)\colon \mathcal{G} \rightarrow [0,1]$](/images/stories/latexuj/2024-11/2024-11-miisazagrafon/img71.png) Lipschitz-folytonos.
Lipschitz-folytonos.
A 2. és 3. tételek és némi elemi analízis segítségével megmutatható, hogy az extremális gráfelmélet minimalizálási problémái (mint a fentiekben tárgyalt példa) garantáltan megoldhatók a grafonok terében. Ezek a grafonmegoldások az 1. tételen keresztül „sablont” adnak közelítő megoldások konstruálásához a véges gráfok terében.
Daniel Glasscock
Fordította: Tóth László Márton, Rényi Alfréd Matematikai Intézet
Irodalom
- [1] C. Borgs, J. T. Chayes, L. Lovász, V. T. Sós, and K. Vesztergombi, Convergent sequences of dense graphs. I. Subgraph frequencies, metric properties and testing, Adv. Math. 219 (2008), no. 6, 1801-1851. MR 2455626 (2009m:05161)
[2] L. Lovász, Large Networks and Graph Limits, American Mathematical Society Colloquium Publications, vol. 60, American Mathematical Society, Providence, RI, 2012. MR 3012035
[3] L. Lovász and B. Szegedy, Limits of dense graph sequences, J. Combin. Theory Ser. B 96 (2006), no. 6, 933-957. MR 2274085 (2007m:05132)
-
Daniel Glasscock az Ohio Állami Egyetem doktorandusz hallgatója volt 2015-ben, amikor a cikk megjelent az AMS-ben. Most Assitant Professor a University of Massachusetts Lowell-en. A fordítást a szerző engedélyével közöljük. (A szerk.)











