Pontokról és alakzatokról — A topológia és a (perzisztens) homológia alapfogalmai

A közelmúltban két cikkfordítás is megjelent az Érintő elektronikus hasábjain, amelyek a perzisztens homológia különböző aspektusait és néhány alkalmazását mutatják be a molekuláris biológiában [13], illetve az elméleti matematikában [14]. Jelen dolgozat célja, hogy – az említett írásokat kiegészítendő – minél szélesebb közönségnek szemléletes (de a matematikai formalizmust sem teljesen nélkülöző) bevezetést nyújtson a témakör, vagyis az alkalmazott algebrai topológia alapjaiba.

Miért éppen a topológia?

Amióta ember az ember, él benne az őt körülvevő világ megismerésének vágya. Így a Föld, illetve a Világegyetem alakjának kérdése is évezredek óta érdeklődés és vita tárgyát képezi. Az a tény, hogy bolygónk felszíne nem lapos korong (ahogy azt sok ősi mitológia hirdette), hanem (megközelítőleg) gömbfelület, az ókor óta ismeretes [1]. Bár a 19. század geometriai forradalma (amelyről az Érintőben is olvashattunk [5]) elvezetett a kozmikus léptékű fizikai törvényszerűségek alaposabb megértéséhez, az univerzum formájának rejtélye azonban napjainkban is izgalmas kutatási terepet biztosít csillagászok, elméleti fizikusok és matematikusok számára egyaránt [12, 19. fejezet].

Leonhard Euler, akinek a nevével később még találkozunk, 1736-ban megoldotta a königsbergi hidak híres problémáját [15], amit sokan a gráfelmélet és a topológia kiindulópontjának tekintenek. Euler ugyanis felismerte, hogy a kérdésre¹ adható válasz nem függ a hidak pontos elhelyezkedésétől, hanem csupán az egyes városrészek között általuk létesített összefüggőségi viszonytól. Ez a fajta absztrakciós szemléletmód az elmúlt évszázadok során rendkívül gyümölcsözőnek bizonyult nemcsak a matematikában, hanem a fizikában és az informatikában, sőt az utóbbi években – a perzisztens homológia révén – az adatfeldolgozásban is.

A topológia a matematikának az az ága, amely bizonyos tág értelemben vett alakzatok (ún. topologikus terek) olyan tulajdonságait vizsgálja, amelyek megmaradnak az alakzat folytonos deformációja során. Egy-egy ilyen tulajdonságot (topologikus) invariánsnak nevezünk, „folytonos deformáció” alatt pedig homeomorfizmust értünk, vagyis olyan $f\colon X \rightarrow Y$ folytonos és kölcsönösen egyértelmű leképezést, amelynek inverze, $f^{-1}\colon Y \rightarrow X$ is folytonos. Ekkor azt mondjuk, hogy $X$ és $Y$ egymással homeomorf topologikus terek és ezt a kapcsolatot $X \cong Y$ relációval jelöljük.

A topologikus tér egy nagyon általános fogalom, azonban a továbbiakban mi csak olyan tereket vizsgálunk, amelyek az euklideszi sík vagy tér bizonyos „szép” részhalmazai. Tekintsük például a félkövér A és O betűket (1. ábra). A 2. ábrán egy folytonos deformációt láthatunk A és O között, amely szemlélteti, hogy A $\cong$ O, vagyis e két betű egymással homeomorf. Talán érezzük, ez azon múlik, hogy mindkét betű „ugyanannyiszor lyukas”, és az is hihetően hangzik, hogy az A, B és C betűk emiatt páronként nem homeomorfak. A következőkben ezt precízzé tesszük, de előtte az olvasót egy kis fejtörésre hívjuk.

1. feladat. Homeomorf-e egymással az A és O betű, amennyiben vastagság nélküli, ideális vonalakkal rajzoljuk meg őket, valahogy úgy, ahogy az a 3. ábrán is látható?

2. feladat. Osztályozzuk a magyar ábécé (vastagság nélküli vonalakkal megrajzolt) betűit aszerint, hogy melyek homeomorfak és melyek nem.

1. ábra

2. ábra

3. ábra

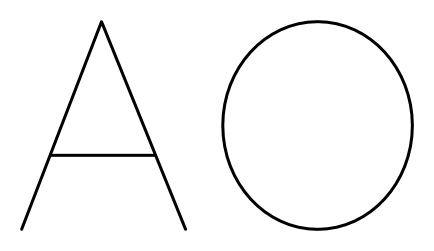
Az 1. feladat megoldása

4. ábra

Megmaradó mennyiségek

Miként tudunk tehát matematikai szigorúsággal megkülönböztetni egymástól olyan topologikus tereket, amelyek nem homeomorfak? A válasz az, hogy alkalmas megmaradó mennyiségek, vagyis invariánsok segítségével!

Szemléletes geometriai példa, amikor síkidomokat szeretnénk osztályozni egybevágóság szerint. Ekkor a terület egy kézenfekvő invariáns: ha ugyanis két síkidom területe különböző, akkor nem lehetnek egybevágók. Fordított esetben azonban semmit sem mondhatunk, hiszen számtalan olyan síkidom létezik, amelyek területe azonos, mégsem egybevágók. A homeomorfizmus erejéig történő klasszifikációban azonban a terület kiszámítása még ennyit sem segít, hiszen ebben a vonatkozásban nem is invariáns. Valami másra van szükségünk.

Bizonyára sok olvasó számára ismerős Euler poliédertétele, amely szerint bármely $P$ konvex poliéderre

$\displaystyle c + l = e + 2,$

(1)

ahol $c$ , $e$ és $l$ rendre $P$ csúcsainak, éleinek és lapjainak számát jelöli. A kockának például 8 csúcsa, 12 éle és 6 lapja van. És valóban: $8 + 6 = 12 + 2$ .

3. feladat. Ellenőrizzük Euler tételét a szabályos testekre (5. ábra).

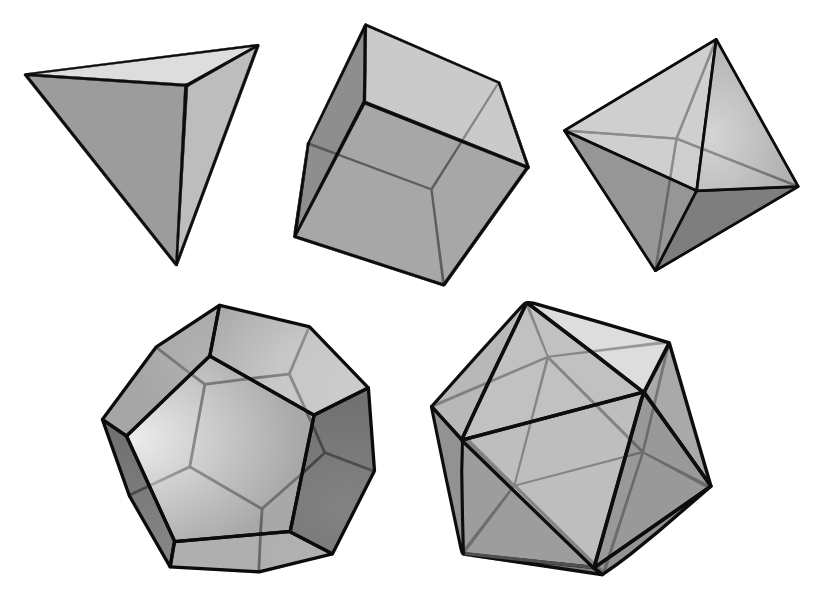
5. ábra. Az öt szabályos test (Wikimedia Commons Contribution)

Mármost egy konvex poliéderre gondolhatunk úgy, mint a gömbfelület egy kombinatorikus modelljére, hiszen azzal homeomorf. Ebben az olvasatban a tétel nem kevesebbet állít, mint azt, hogy a $\chi(P) = c-e+l$ kifejezés értéke független a modell-poliéder megválasztásától.

Valójában azonban ennél sokkal több is igaz. Az Euler-féle poliédertétel ugyanis tetszőleges, nem-konvex poliéderre is érvényes marad abban az értelemben, hogy $\chi(P)$ értéke csupán az adott $P$ poliéder topologikus típusától függ. Például az úszógumi (matematikai nevén: tórusz) felületével homeomorf poliéderekre ez az érték mindig 0, a kétszemélyes úszógumi esetében pedig $-2$ (lásd a 6. és 7. ábrákat).

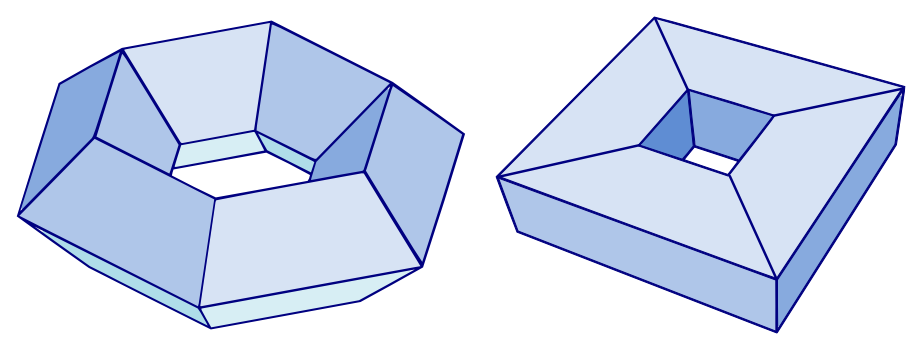
6. ábra. A tórusz két poliédermodellje

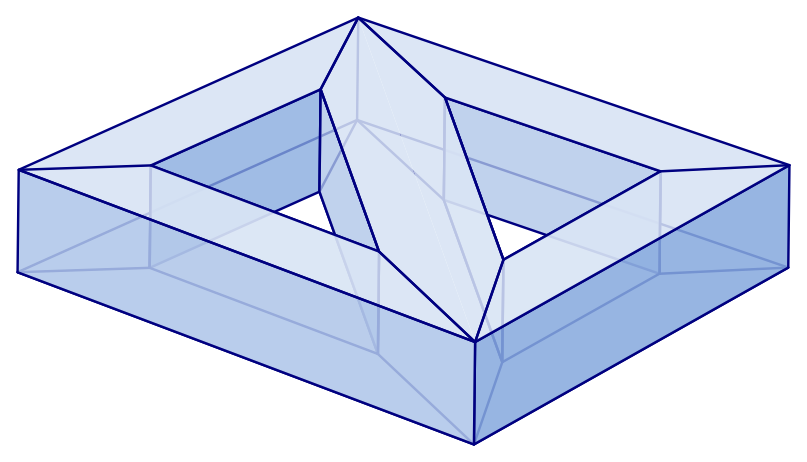
7. ábra. Egy kétszemélyes úszógumi. Öt konvex poliéderből ragasztottuk össze, majd „kiütöttük” a belső falakat. Meglehetősen kényelmetlennek tűnik.

A szóban forgó $\chi(P)$ számot a $P$ poliéder Euler-karakterisztikájának nevezzük. Fenti megfigyeléseinket a következőképp foglalhatjuk össze.

1. tétel (Euler-féle általános poliédertétel). Legyen $P$ tetszőleges poliéder.³ Jelölje $c, e$ és $l$ rendre $P$ csúcsainak, éleinek és lapjainak számát. A

$\displaystyle \chi(P) = c - e + l$

(2)

képlettel definiált Euler-karakterisztika topologikus invariáns, vagyis egymással homeomorf $P$ , $P'$ poliéderek esetén $\chi(P) = \chi(P')$ .

Az 1. tétel bizonyítása meghaladná dolgozatunk (terjedelmi) kereteit. Az érdeklődő olvasót azonban arra biztatjuk, gondolja át, hogyan (nem) változik az Euler-karakterisztika, ha egy adott poliéder valamely lapját kisebbekre bontjuk (akár új csúcsok felvételével), vagy fordítva: ha két élszomszédos lapot egybenyitunk közös élük kitörlésével. Ezekkel és hasonló megfontolásokkal a bizonyításhoz is eljuthatunk [11, 13. fejezet].

Következmény. Jelölje $\mathbb{S}^2$ , $\mathbb{T}^2$ és $\mathbb{T}^2\char93 \mathbb{T}^2$ rendre a gömbfelületet, a tóruszt és a kétszemélyes úszógumi felületét. Ekkor $\chi(\mathbb{S}^2) = 2$ , $\chi(\mathbb{T}^2) = 0$ , valamint $\chi(\mathbb{T}^2\char93 \mathbb{T}^2) = -2$ . Az 1. tétel értelmében tehát $\mathbb{S}^2$ , $\mathbb{T}^2$ és $\mathbb{T}^2\char93 \mathbb{T}^2$ páronként nem-homeomorf topologikus terek.

4. feladat. A kétszemélyes úszógumi felületét az imént $\mathbb{T}^2\char93 \mathbb{T}^2$ -vel jelöltük. Vajon milyen műveletet kódol a $\char93$ szimbólum? Számítsuk ki továbbá a $10$ személyes úszógumi Euler-karakterisztikáját.

5. feladat. Gondoljuk meg, hogy az 1. tétel állítása érvényes peremes felületekre is (olyan felületekre, amelyeket egy poliéderből kaphatunk néhány lapjának elhagyásával). Ezt követően bizonyítsuk be, hogy a félkövér A, B és C betűk egymással páronként nem-homeomorfak.

Homológiaelmélet nagyon röviden

Ebben a szakaszban megismerkedünk a homológia fogalmával, amit Henri Poincaré vezetett be Analysis situs című 1895-ben megjelent közleményében [8]. A cikk és 1899–1904 között publikált függelékei paradigmaváltást hoztak a topológiában azáltal, hogy a „terek tanulmányozását” összekapcsolták a matematika egy látszólag távoli ágával, az algebrával [9]; kérdésfelvetései pedig meghatározták a 20. század geometriai és topológiai kutatásait [7].

Első megközelítésben a homológia egy olyan matematikai formalizmus, amelynek segítségével számszerűsíthetjük egy topologikus tér komponenseit, lyukait, üregeit és további összefüggőségi viszonyait, mindezt oly módon, hogy a térhez algebrai objektumokat, ún. homológiacsoportokat rendelünk, amelyeket együttesen a tér homológiájának nevezünk. Az Euler-karakterisztikához hasonlóan a homológia is topologikus invariáns, azonban több információt hordoz annál. Például a homológia ismeretében kiszámítható az Euler-karakterisztika (10. feladat), de fordítva ez általában nem igaz.

Az alábbiakban háromszöglapokból felépíthető felületek (más néven háromszögelések) homológiáját definiáljuk. Ilyen alakzatok láthatók 8. ábrán.

8. ábra. Az „ő” betű és a tórusz egy-egy háromszögelése

Legyen $X = (V,E,T)$ egy háromszögelés, ahol $V$ , $E$ és $T$ rendre a csúcsok (0-dimenziós lapok, röviden 0-lapok), élek ( $1$ -lapok) és háromszöglapok ( $2$ -lapok) halmazát jelöli.⁴ A fő kihívás, hogy miként határozzuk meg $X$ lyukait, illetve üregeit, hiszen ezek a térnek nem is részei. Poincaré azt a közvetett utat javasolja, hogy próbáljuk leírni $X$ azon részhalmazait, amelyek a lyukakat és üregeket körülveszik.⁵ Ennek első lépéseként tekintsük a

$\displaystyle C_0 = \mathcal{P}(V), \quad C_1 = \mathcal{P}(E)$ és $\displaystyle \quad C_2 = \mathcal{P}(T)$

hatványhalmazokat.⁶ A $C_i$ halmaz elemeit $i$ -dimenziós láncoknak (röviden $i$ -láncoknak) nevezzük ( $i = 0,1,2$ ). Vegyük észre, hogy a $C_i$ halmazon értelmezhető egy „összeadás”: $\alpha,\beta \in C_i$ esetén jelölje $\alpha + \beta$ a két halmaz szimmetrikus differenciáját. Ezzel a művelettel ellátva $C_i$ kommutatív csoportot alkot, amelynek neutrális eleme az üres halmaz ( $\emptyset$ ) és bármely elem ellentettje önmaga. (A 9. ábra a $C_2$ -beli összeadást szemlélteti.)

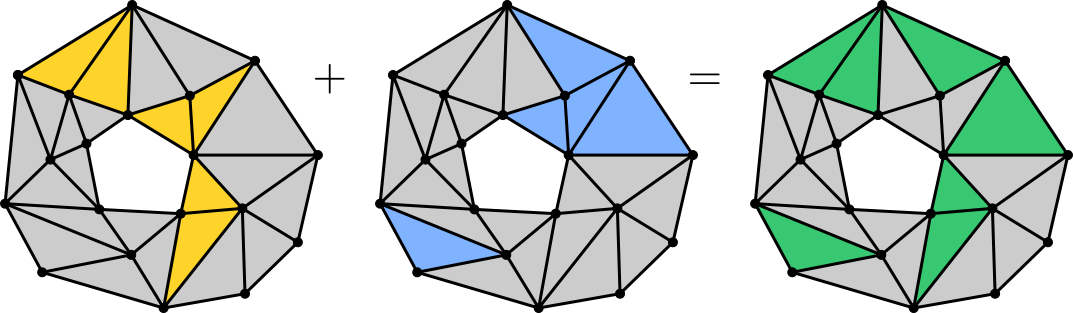
9. ábra. Összeadás $C_2$ -ben

A második lépésben azt szeretnénk megérteni, hogy a szomszédos dimenziójú láncok milyen viszonyban állnak egymással. Ezt a kapcsolatot az ún. határleképezés (jelölésben $\partial$ ) segítségével tárhatjuk fel, amely egy $\alpha$ $i$ -lánchoz hozzárendeli annak $(i-1)$ -dimenziós $\partial\alpha$ határát, ami pontosan azokból az $(i-1)$ -lapokból áll, amelyeket páratlan sok $\alpha$ -beli $i$ -lap tartalmaz. Egy 0-lánc határa definíció szerint $\emptyset$ . Régi bölcsesség, hogy egy kép többet mond ezer szónál: a 10. ábra a határleképezést mutatja be működés közben egy-egy $2$ -lánc (kék) és $1$ -lánc (piros) példáján keresztül.

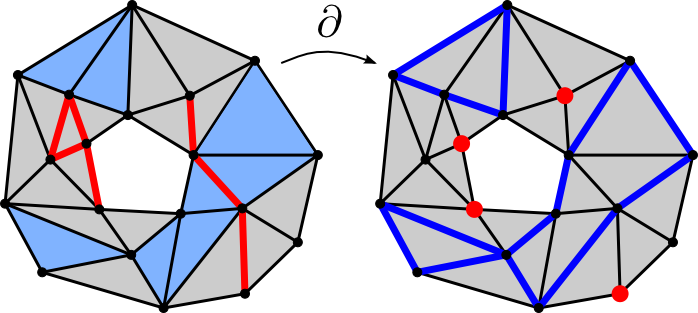
10. ábra. A homológia „lelke” a határleképezés

Már nem járunk messze a homológiacsoportok definíciójától. A határleképezés következő tulajdonságai kulcsfontosságúak.

6. feladat. Bizonyítsuk be, hogy

két lánc összegének határa megegyezik a tagok határainak összegével, azaz 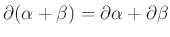$\partial(\alpha+\beta) = \partial\alpha + \partial\beta$ , valamint azt, hogy
„határ határa üres”, vagyis 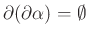$\partial(\partial\alpha) = \emptyset$ teljesül bármely $\alpha$ esetén.

A láncok között vannak olyanok, amelyek kitüntetett figyelmet érdemelnek. Ciklusnak nevezünk egy olyan láncot, amelynek határa üres. A határ pedig értelemszerűen olyan lánc, amely előáll $\partial$ képeként. Az $i$ -ciklusok halmazát $Z_i$ , míg az $i$ -határokét $B_i$ jelöli. (Esetünkben $B_2 = \emptyset$ .) Formálisan,

$\displaystyle Z_i$	$\displaystyle = \{\alpha \in C_i \mid \partial \alpha = \emptyset\},~$ és
$\displaystyle B_i$	$\displaystyle = \{\beta \in C_i \mid \exists\gamma\in C_{i+1} : \partial \gamma = \beta\}.$

Két lánc $\gamma,\gamma' \in C_i$ homológ, ha az összegük határ, vagyis $\gamma + \gamma' \in B_i$ . A homológia szempontjából az ilyen láncokat nem szeretnénk megkülönböztetni. Jelölje $[\gamma]$ a $\gamma$ -val homológ $i$ -láncok halmazát, azaz $\gamma$ homológiaosztályát.

7. feladat. Mutassuk meg, hogy a homológiaosztályok $C_i$ partícióját adják, azaz $\gamma, \delta \in C_i$ esetén vagy $[\gamma] \cap [\delta] = \emptyset$ , vagy pedig $[\gamma]=[\delta]$ .

A 6/2. feladatból azonnal következik, hogy $B_i \subseteq Z_i$ , azaz minden határ egyúttal ( triviális) ciklus is. Az általunk vizsgált összefüggőségi viszonyok (pl. lyukak) vonatkozásában azonban pont azok a ciklusok relevánsak, amelyek nem-triviálisak, vagyis nem állnak elő határként (vö. 11. és 12. ábrák). Ezzel pedig el is érkeztünk a homológia fogalmához.

Az $X$ háromszögelés $H_i = H_i(X)$ $i$ -edik homológiacsoportját az $i$ -ciklusok homológiaosztályai alkotják, amelyek között az összeadást a

$\displaystyle [z]+[z']=[z+z']$

(3)

képlettel definiáljuk. Belátható, hogy egy topologikus invariánst kapunk [4].

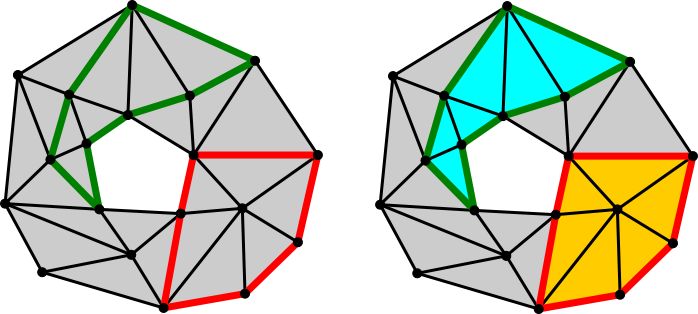
11. ábra. Két triviális $1$ -ciklus

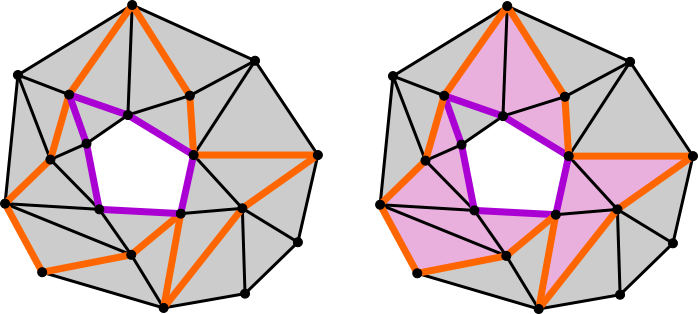
12. ábra. Két nem-triviális $1$ -ciklus amelyek homológak

8. feladat. Igazoljuk, hogy a 12. ábra ciklusai – a 11. ábrán láthatókkal ellentétben – nem-triviálisak, azaz nem kaphatók meg néhány háromszöglap uniójának határaként.

9. feladat. Tekintsük az „ő” betű háromszögelését a 8. ábrán. Hány eleme van a $H_0($ ő $)$ homológiacsoportnak? És $H_1($ ő $)$ -nek?

Homológia és lineáris algebra

A lineáris algebrában jártas olvasó az $i$ -láncok $C_i$ csoportjára gondolhat úgy, mint egy, az $\mathbb{F}_2$ test feletti vektortérre, amelyet az $i$ -lapok – mint báziselemek – generálnak. Például $C_0$ az $\mathbb{F}_2^{\vert V\vert}$ vektortérrel izomorf. Ha pedig $\partial_i$ jelöli a $\partial$ leképezés $C_i$ -re történő megszorítását, akkor a 6. feladat értelmében $\partial_i\colon C_i \rightarrow C_{i-1}$ egy lineáris leképezés, valamint $\operatorname{im}\partial_{i+1} \subseteq \ker \partial_i$ . Végül $H_i = \ker \partial_i / \operatorname{im}\partial_{i+1}$ , ahol a jobb oldalon két vektortér hányadostere áll. Fontos invariáns mennyiségek továbbá az egyes homológiacsoportok (mint vektorterek) dimenziói, vagyis a mögöttes topologikus tér ún. Betti-számai:

$\displaystyle b_i = \dim_{\mathbb{F}_2}H_i.$

(4)

Segítségükkel immár matematikai precizitással számlálhatjuk le egy háromszögelés komponenseit ( $b_0$ ), lyukait ( $b_1$ ) és üregeit ( $b_2$ ). Valóban, az „ő” betű esetén $(b_0,b_1,b_2) = (3,1,0)$ , míg a tóruszra ugyanez $(1,2,1)$ , vö. 8. ábra.

Ennek a személetmódnak az alkalmazások szempontjából is kitüntetett jelentősége van, hiszen a lineáris algebra számítási módszerei tipikusan jól automatizálhatók és az algoritmusok (gyors) futási ideje „nagyméretű” háromszögelések esetében is lehetővé teszi a homológia kiszámítását [3].

10. feladat. Igazoljuk, hogy bármely $X = (V,E,T)$ háromszögelésre

$\displaystyle b_0 - b_1 + b_2 = \vert V\vert - \vert E\vert + \vert T\vert = \chi(X).$

(Segítség: Alkalmazzuk a lineáris algebrából ismert dimenziótételt.)

Egy ponthalmaz alakja

Napjainkban számos területen merül fel az igény, hogy egy adott ponthalmaz „alakját”, illetve topologikus jellemzőit meghatározzuk, ezáltal mélyebb strukturális ismereteket szerezve a vizsgált adatokra vonatkozóan [13]. A topologikus adatelemzés (angolul: topological data analysis, röviden TDA) – az alkalmazott matematika egy fiatal, dinamikusan fejlődő ága – ezt az igényt próbálja kielégíteni. Sarokköve a perzisztens homológia, amelynek alapötletét az alábbiakban néhány konkrét példán keresztül szemléltetjük.

A témakörben való elmélyüléshez a [3] könyv III. részét, valamint a [2], [6] és [14] áttekintő cikkeket ajánljuk.

13. ábra. Az „A”, illetve „O” betűkből véletlenszerűen mintavételezett 40-40, valamint 200-200 pont

Legyen $Q$ síkbeli (általános helyzetű⁷) pontok véges halmaza (13. ábra). A kövekezőkben értelmezni szeretnénk $Q$ „alakját”, mégpedig úgy, hogy felépítjük rá háromszögeléseknek egy egymásba ágyazott sorozatát, vagyis filtrációját. A konstrukció nulladik lépésében tekintsük a $Q$ által meghatározott Voronoj-diagramot, ami a sík egy

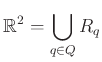
$\displaystyle \mathbb{R}^2 = \bigcup_{q \in Q}R_q$

felbontása, ahol $R_q = \{x \in \mathbb{R}^2 \mid \forall q' \in Q : \Vert x-q\Vert \leq \Vert x-q'\Vert\}$ . Az $R_q$ halmazt a $q$ ponthoz tartozó Voronoj-cellának nevezzük és a sík azon pontjaiból áll, amelyek $q$ -tól legfeljebb olyan távol vannak, mint $Q$ összes többi pontjától. Magyarán $R_q$ a $q$ pont vonzáskörzete (lásd a 14. és 16/(i). ábrákat).

14. ábra. Egy síkbeli ponthalmaz Voronoj-diagramja (Szerző: Balu Etrl [CC-BY-SA 3.0], Wikimedia Commons)

Rögzítsünk most egy $r \in \mathbb{R}_{\geq 0}$ nemnegatív valós paramétert. A $Q$ halmaz $\operatorname{Alfa}_r(Q) = (V,E,T)$ $r$ -sugarú alfa-komplexusa az a háromszögelés, amelyre

$V = Q$ ;
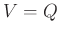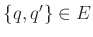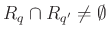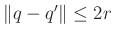$\{q,q'\} \in E$ , amennyiben $R_q \cap R_{q'} \neq \emptyset$ és $\Vert q-q'\Vert \leq 2r$ ; valamint
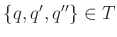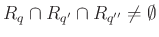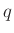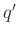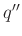$\{q,q',q''\} \in T$ pontosan akkor, ha $R_q \cap R_{q'} \cap R_{q''} \neq \emptyset$ továbbá a $q$ , $q'$ és $q''$ pontok köré írt 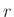$r$ sugarú zárt körlapok metszete nem üres.

Szavakkal kifejezve, az $\operatorname{Alfa}_{r}(Q)$ alfa-komplexus a $Q$ -beli pontok köré írt $r$ sugarú körlapok átfedési viszonyait „tárolja” azzal a megkötéssel, hogy csak olyan körlapok kapcsolatát veszi figyelembe, amelyek középpontjai egymással szomszédos Voronoj-cellákban találhatók.

Vegyük észre, hogy $r_1 < r_2 < r_3 < \cdots$ esetén

$\displaystyle \operatorname{Alfa}_{r_1}(Q) \subseteq \operatorname{Alfa}_{r_2}(... ...\operatorname{Alfa}_{r_3}(Q) \subseteq \cdots \subseteq \operatorname{Del}(Q),$

ahol $\operatorname{Del}(Q)$ a $Q$ ponthalmaz ún. Delaunay-háromszögelése. Az $\{\operatorname{Alfa}_{r}(Q) \mid r \in \mathbb{R}_{\geq 0}\}$ háromszögelések egymásba ágyazott (véges!) családját ezért $Q$ Delaunay-filtrációjának nevezzük (16. ábra).

11. feladat. Gondoljuk meg, hogy az $\{\operatorname{Alfa}_{r}(Q) \mid r \in \mathbb{R}_{\geq 0}\}$ családban csak véges sok különböző alfa-komplexus szerepel.

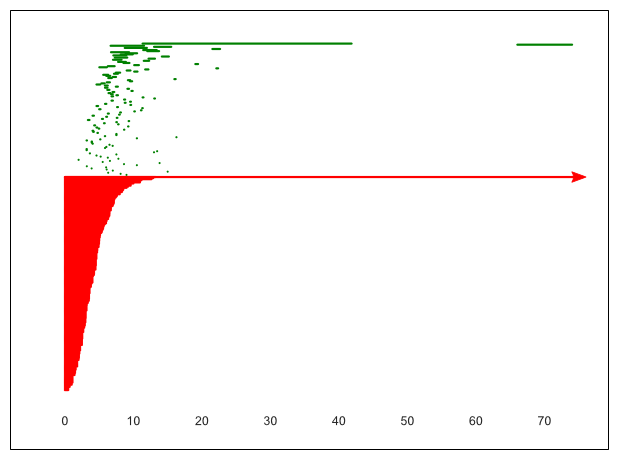
Zárásképp definiáljuk egy adott filtráció perzisztencia-vonalkódját, amely egyetlen grafikonba sűríti a filtráció során fellépő alfa-komplexusok homológiáját, pontosabban Betti-számait. Lényegében ezt nevezzük a filtráció perzisztens homológiájának. A vonalkód segítségével ugyanis pontosan végigkövethetjük, hogyan „születnek” és „halnak meg” $\operatorname{Alfa}_{r}(Q)$ homológiáosztályai az $r$ paraméter értékének megváltoztatása során (15. ábra).

Formális definíció helyett tekintsük a 16. ábrán látható példát. Kezdetben $\operatorname{Alfa}_{0}(Q)$ négy diszkrét pontból áll, vagyis ekkor $b_0 = 4$ , $b_1=0$ . Az $r$ sugár értéket növelve, egy ideig „semmi sem történik”, azonban $\operatorname{Alfa}_{32}(Q)$ -ban megjelenik az első él, amelynek következtében a komponensek száma eggyel csökken, így $b_0 = 3$ , $b_1=0$ . Amikor $r = 37$ , „megszületik” az első nem-triviális 1-ciklus; a háromszögelés ekkor már egy ideje egyetlen komponensből áll: $b_0 = 1$ , $b_1=1$ . Azonban $\operatorname{Alfa}_{39}(Q)$ -ben megjelenik az a háromszög, amely „megöli” az előbbi 1-ciklust: $b_0 = 1$ , $b_1=0$ . Végül $\operatorname{Alfa}_{52}(Q)$ -ben egyszerre jelenik meg az utolsó él és a rá illeszkedő (utolsó) háromszög, vagyis ekkor (és ezután már) semmi sem változik a homológia szempontjából.

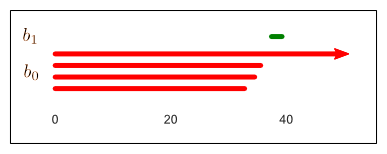
15. ábra. A 16. ábrán bemutatott filtráció perzisztencia-vonalkódja16. ábra. Egy ponthalmaz Delaunay-filtrációjának néhány állomása

Köszönetnyilvánítás.

A Függelékben szereplő, az „A” és „O” betűk filtrációit bemutató animációkat alkotó ábrákat és vonalkódokat kollégáim, Katharina Ölsböck, illetve Hubert Wagner készítették (pontosabban varázsolták) elegáns, pársoros Python szkriptjeikkel. Segítségüket hálásan köszönöm.

Köszönöm továbbá Stipsicz Andrásnak a dolgozat vázlatával kapcsolatban tett értékes megjegyzéseit.

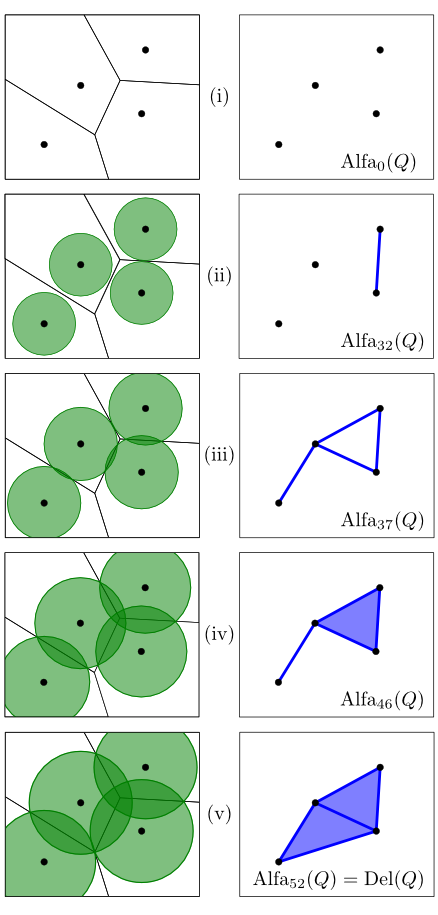
16. ábra. Egy ponthalmaz Delaunay-filtrációjának néhány állomása

Irodalomjegyzék

[1] Csaba György Gábor: Évezredek óta tudjuk, hogy nem lapos – a Föld gömb alakjának ókori bizonyítékaiból. http://mta.hu/tudomany_hirei/evezredek-ota-tudjuk-hogy-nem-lapos-a-fold-gomb-alakjanak-okori-bizonyitekaibol-107936. Hozzáférés: 2018. 09. 02.

[2] Herbert Edelsbrunner–John Harer: Persistent homology – a survey. In Surveys on discrete and computational geometry. Contemp. Math. sorozat, 453. köt. 2008, American Mathematical Society, Providence, RI, 257–282. p. https://doi.org/10.1090/conm/453/08802.

[3] Herbert Edelsbrunner–John L. Harer: Computational topology: an introduction. 2010, American Mathematical Society, Providence, RI, xii+241. p.

[4] Fehér Lászó: Homológia-elmélet (egyetemi jegyzet), 2012. http://web.cs.elte.hu/~lfeher/honlap/algtop2012t/homologia.pdf. Hozzáférés: 2018. 09. 01.

[5] G. Horváth Ákos: Nem-euklideszi geometriák, avagy milyen a világ? Konstans görbületű terek. Érintő – Elektronikus Matematikai Lapok, 2017. június. http://www.ematlap.hu/index.php/tudomany-tortenet-2017-06/510-nem-euklideszi-jav.

[6] Robert Ghrist: Barcodes: the persistent topology of data. Bull. Amer. Math. Soc. (N.S.), 45. évf. (2008) 1. sz., 61–75. p. https://doi.org/10.1090/S0273-0979-07-01191-3.

[7] Moussong Gábor: A Poincaré-sejtés (Tudományos népszerűsítő előadások a Fővárosi Fazekas Gimnáziumban). A 2006. szeptember 19-én elhangzott előadás alapján az összefoglalót készítette Balambér Dávid, Bohus Péter, Hraskó András és Moussong Gábor. http://matekold.fazekas.hu/portal/eloadas/2006/eloadas_2006_09_19_moussong.html. Hozzáférés: 2018. 09. 01.

[8] Henri Poincaré: Analysis situs. Journal de l'Ecole Polytechnique, 1. évf. (1895), 1–121. p.

[9] Henri Poincaré: Papers on topology: Analysis situs and its five supplements. History of Mathematics sorozat, 37. köt. 2010, American Mathematical Society, Providence, RI; London Mathematical Society, London, xx+228. p. Fordította és a bevezetőt írta: John Stillwell.

[10] Stipsicz András: Négydimenziós sokaságok topológiája – áttekintés. Matematikai Lapok. Új sorozat, 6. évf. (1996) 3–4. sz., 1–27. p.

[11] Szűcs András: Topológia (egyetemi jegyzet), 2018. http://web.cs.elte.hu/~szucs/Top1-2.pdf. Hozzáférés: 2018. 09. 01.

[12] Jeffrey R. Weeks: A tér alakja: felületek és háromdimenziós alakzatok ábrázolása. 2009, Typotex Kiadó, Budapest, 213. p. Fordította: Stipsicz András és Szilárd Ágnes.

[13] Guo-Wei Wei: Biomolekuláris adatok elemzése perzisztens homológia segítségével. Érintő – Elektronikus Matematikai Lapok, 2018. június. http://ematlap.hu/index.php/gazda-g-sag-2018-06/689-biomolekularos-adatok-elemzese-perzisztens-homologia-segitsegevel. Fordította: Huszár Kristóf és Stipsicz András.

[14] Shmuel Weinberger: Mi is ... az a perzisztens homológia? Érintő – Elektronikus Matematikai Lapok, 2018. szeptember. http://ematlap.hu/index.php/tudomany-tortenet-2018-09/766-mi-is-az-a-perzisztens-homologia. Fordította: Stipsicz András.

[15] Wikipédia: Königsbergi hidak problémája – Wikipédia, 2018.

https://hu.wikipedia.org/w/index.php?title=K%C3%B6nigsbergi_hidak_probl%C3%A9m%C3%A1ja Hozzáférés: 2018. 09. 02.

Függelék: Filtrációk és vonalkódok

17. ábra. Az „A”-ból mintavételezett 40 pont egyre növekvő $r$ surgarú környezetei, $r \in \{20,50,80,120\}$ , valamint a megfelelő alfa-komplexusok

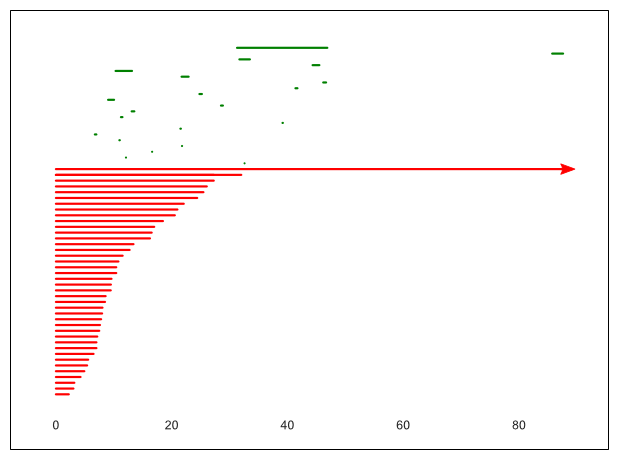
18. ábra. A 17. ábrán bemutatott filtráció perzisztencia-vonalkódja

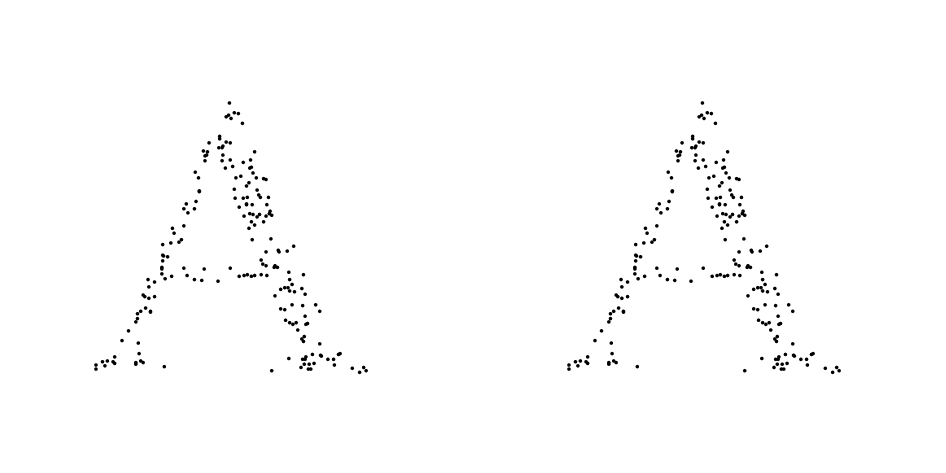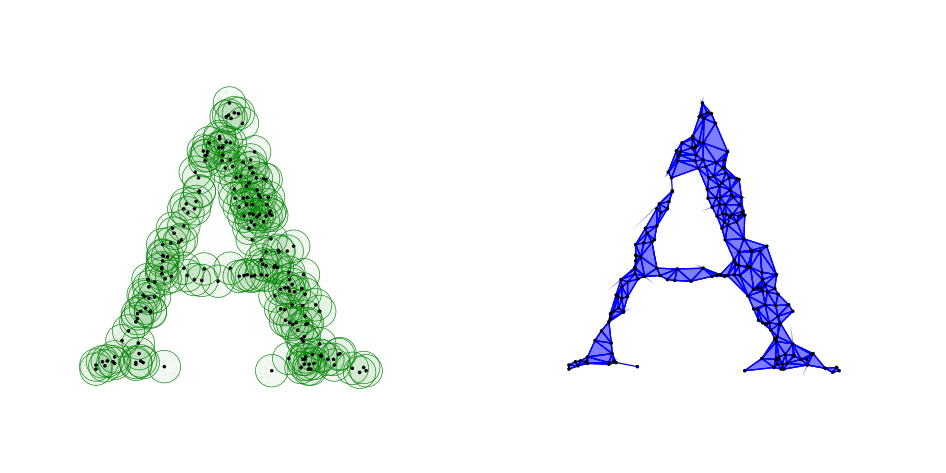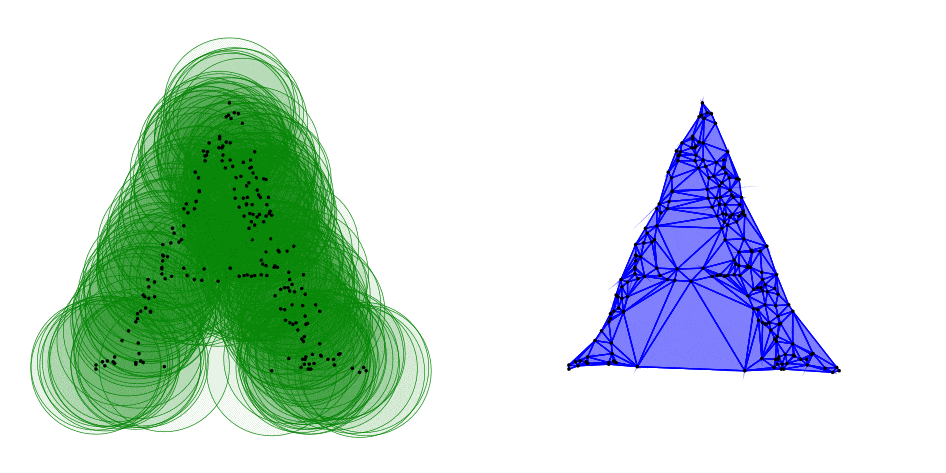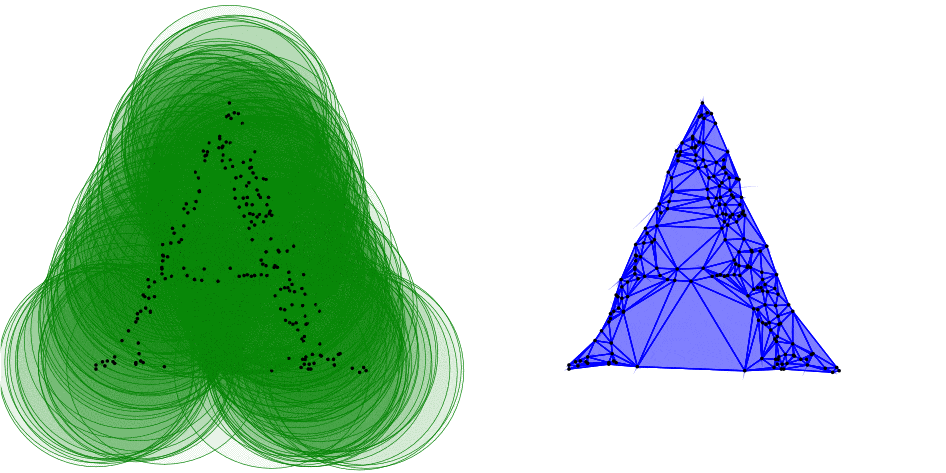
19. ábra. Az „A”-ból mintavételezett 200 pont egyre növekvő $r$ surgarú környezetei, $r \in \{20,50,80,120\}$ , valamint a megfelelő alfa-komplexusok

20. ábra. A 19. ábrán bemutatott filtráció perzisztencia-vonalkódja

21. ábra. Az „O”-ból mintavételezett 40 pont egyre növekvő $r$ surgarú környezetei, $r \in \{20,50,80,120\}$ , valamint a megfelelő alfa-komplexusok

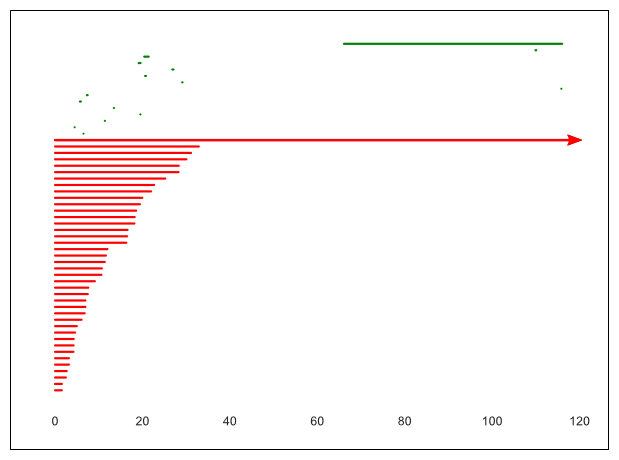
22. ábra. A 21. ábrán bemutatott filtráció perzisztencia-vonalkódja

23. ábra. Az „O”-ból mintavételezett 200 pont egyre növekvő $r$ surgarú környezetei, $r \in \{20,50,80,120\}$ , valamint a megfelelő alfa-komplexusok

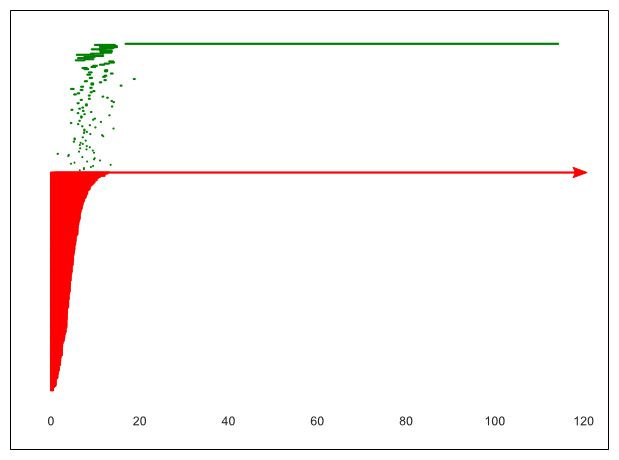
24. ábra. A 23. ábrán bemutatott filtráció perzisztencia-vonalkódja

Lábjegyzetek

¹ Lehetséges-e olyan körsétát tenni az akkori Königsberg (ma Kalinyingrád) belvárosában, amely a Prégel folyón átívelő összes hídon pontosan egyszer halad végig?

² Nevezetes fogalom az ún. homotopikus ekvivalencia, amely a homeomorfizmusnál gyengébb kapcsolatot létesít topologikus terek között. A dolgozatunk középpontjában álló homológiacsoportok például homotopikus invariánsok. Mindez azonban túlmutat vizsgálódásaink keretein. Az érdeklődő olvasónak a [11] és [4] egyetemi jegyzeteket ajánljuk.

³ A tétel még tovább általánosítható ún. cella-komplexusokra [11, 11. és 13. fejezetek].

⁴ Az 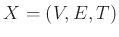$X = (V,E,T)$ jelölés a gráfelméletből jól ismert „ 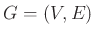$G = (V,E)$ ” jelölés analógja.

⁵ Ebben a dolgozatban kizárólag ún. 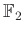$\mathbb{F}_2$ -együtthatós szimpliciális homológiával foglalkozunk. Ez egyrészt lehetővé teszi, hogy számos technikai részlettől (pl. a lapok irányításától) eltekintsünk, másrészt ilyenkor egy láncra gondolhatunk úgy, mint lapok egy részhalmazára, ami egyszerűsíti a tárgyalást. Továbbá a számítógépes topológiában az 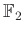$\mathbb{F}_2$ -együtthatós homológia a leginkább elterjedt [3, IV. fejezet]. A homológia azonban messzemenőkig általánosítható mind az együtthatók, mind a vizsgált terek tekintetében [4].

⁶ Egy 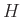$H$ halmaz 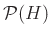$\mathcal{P}(H)$ hatványhalmaza a 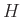$H$ összes részhalmazainak halmaza.

⁷ Ebben a cikkben egy síkbeli ponthalmazt akkor tekintünk általános helyzetűnek, ha semelyik három pont nincs egy egyenesen és semelyik négy nincs egy körön.

Huszár Kristóf

Huszár Kristóf 2013-ban végzett az ELTE Matematika BSc szakán, matematikus szakirányon. Jelenleg az Institute of Science and Technology Austria PhD hallgatója Uli Wagner kutatócsoportjában. Főbb érdeklődési területe a kombinatorikus topológia.