A 2020-21-es tanév Országos Középiskolai Tanulmányi versenye is hasonlóan alakult a pandémia miatt, mint az előtte levő évben. Mindkét esetben a matematika OKTV gimnáziumi (II-es) kategória első és második fordulóját meg lehetett rendezni, de a tavaszi terminusra eső döntőre már nem került sor. Az alábbiakban az említett kategória második fordulójának negyedik feladatát vesszük alaposabban szemügyre.
A versenyt kevésbé ismerők kedvéért nézzük meg, hogy is épül fel az OKTV verseny a II-es kategóriában. Általában az őszi szünet és a Mikulás között zajlik az első, iskolai forduló, január második felében a második forduló, majd márciusban a döntő. Az első fordulóban résztvettek 10 százaléka, de legfeljebb 300 diák juthat a másodikba, majd a döntőbe a legjobb 50 kerülhet. Minden fordulóban öt óra áll a versenyzők rendelkezésére, hogy megírják dolgozatukat. Az érettségihez hasonlóan zsebszámológép használható. Az egyes fordulókban szereplő feladatokat igyekeznek úgy összeállítani az Oktatási Hivatal által felkért bizottság tagjai, hogy minden fordulóban legyen nehezebb és könnyebb feladat is, lehetőleg változatos témák szerepeljenek. Hagyományosan az elsőben öt, a másodikban négy, a harmadikban három feladat kerül kitűzésre.
A bevezetőben említett feladat kapcsán a dolgozatok javításánál már kiderült, hogy a javítási útmutatóban szereplő viszonylag rövid megoldást nagyon kevesen találták meg és jóval hosszadalmasabb úton jutottak el a válaszhoz. Dr. Horváth Eszter tanárnő is felhívta erre a figyelmemet és ő javasolta, hogy érdemes lenne a feladatot egy Érintő-cikk keretében kicsit körbejárni. Erre invitálom most az Olvasót. A feladat szövege a következő:
Legyen 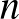 pozitív egész. Vegyünk
pozitív egész. Vegyünk 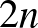 darab különböző prímszámot, jelölje szorzatukat
darab különböző prímszámot, jelölje szorzatukat 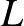 . Tekintsük azon pozitív egész
. Tekintsük azon pozitív egész 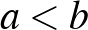 számokat, amelyekre
számokat, amelyekre 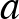 osztója
osztója 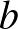 -nek és
-nek és 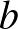 osztója
osztója 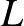 -nek. Igazoljuk, hogy ezen
-nek. Igazoljuk, hogy ezen 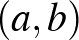 párok száma 5-tel osztható.
párok száma 5-tel osztható.
A feladat a számelmélet témakörébe vezet, oszthatóság szerepel benne. A továbbiakban nem hangsúlyozzuk minden alkalommal, hogy csak a pozitív egészek körében fogunk dolgozni. Mielőtt teljes megoldást adnánk, először ismerkedjünk, barátkozzunk a feladat szövegével. Nézzük meg egy kicsi, konkrét számon, miket kell megszámolni. Az 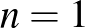 a lehető legkisebb eset, válasszük a két legkisebb prímet, a 2-őt és a 3-at. Ekkor
a lehető legkisebb eset, válasszük a két legkisebb prímet, a 2-őt és a 3-at. Ekkor 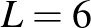 , ennek osztói az 1, 2, 3, 6 számok, ezek lehetnek az
, ennek osztói az 1, 2, 3, 6 számok, ezek lehetnek az 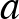 és
és 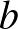 értékek. Ezek után egyszerű felsorolással megkereshetjük a megfelelő
értékek. Ezek után egyszerű felsorolással megkereshetjük a megfelelő 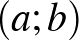 párokat: (1;2), (1;3), (1;6), (2;6), (3;6). A megfelelő párok száma öt, ami osztható 5-tel, így ekkor valóban teljesülnek a feladat feltételei. Miközben ezt kiszámoltuk, azonnal tehetünk két észrevételt:
párokat: (1;2), (1;3), (1;6), (2;6), (3;6). A megfelelő párok száma öt, ami osztható 5-tel, így ekkor valóban teljesülnek a feladat feltételei. Miközben ezt kiszámoltuk, azonnal tehetünk két észrevételt:
(i) Egy 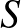 szám osztóinak számát a prímtényezős felbontás ismeretében meghatározhatjuk. Legyen
szám osztóinak számát a prímtényezős felbontás ismeretében meghatározhatjuk. Legyen
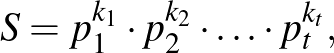
jelölje 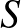 osztóinak számát
osztóinak számát 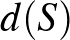 . Ekkor
. Ekkor
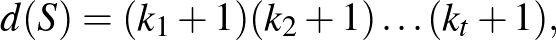
ezt a versenyzőknek nem kellett külön bebizonyítani, nyugodtan hivatkozhattak rá a tananyag részeként.
(ii) A feladat szövegében szerepel az oszthatósági feltételen kívül az 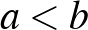 feltétel. Kényelmesebb először az összes oszthatósági feltételnek megfelelő
feltétel. Kényelmesebb először az összes oszthatósági feltételnek megfelelő 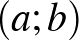 számpárt megkeresni, majd ezek számából levonni az
számpárt megkeresni, majd ezek számából levonni az 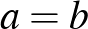 eseteket. Ez az
eseteket. Ez az 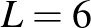 -nál azt jelenti, hogy összesen 9 számpár van, de ezek közül négyet nem kell számolni, amikor
-nál azt jelenti, hogy összesen 9 számpár van, de ezek közül négyet nem kell számolni, amikor 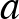 és
és 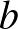 egyaránt egyenlő az 1, 2, 3, 6 számok valamelyikével.
egyaránt egyenlő az 1, 2, 3, 6 számok valamelyikével.
Első (kicsit hosszabb) megoldás:
Az (ii) megjegyzés alapján a megfelelő 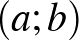 számpárok leszámolását úgy végezzük, hogy először megengedjük az
számpárok leszámolását úgy végezzük, hogy először megengedjük az 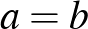 esetet, majd az így kapott számból levonjuk a végén ezeket. Mivel
esetet, majd az így kapott számból levonjuk a végén ezeket. Mivel 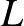 prímtényezős felbontásában
prímtényezős felbontásában 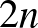 darab különböző prím szerepel, továbbá mindegyik az első hatványon van, ezért a lehetséges
darab különböző prím szerepel, továbbá mindegyik az első hatványon van, ezért a lehetséges 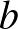 osztókat úgy kapjuk, hogy a
osztókat úgy kapjuk, hogy a 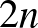 prím közül néhányat beleteszünk
prím közül néhányat beleteszünk 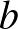 -be. Ha
-be. Ha 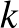 darabot választunk, akkor az ilyen
darabot választunk, akkor az ilyen 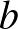 -k száma
-k száma 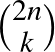 . Amennyiben
. Amennyiben 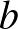 -ben
-ben 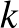 darab különböző prím van, mindegyik a feladat szövege szerint nyilván első hatványon, akkor a
darab különböző prím van, mindegyik a feladat szövege szerint nyilván első hatványon, akkor a 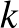 darab prím mindegyikéről egymástól függetlenül eldönthatjük, hogy beletesszük
darab prím mindegyikéről egymástól függetlenül eldönthatjük, hogy beletesszük 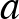 prímtényezős felbontásába vagy sem. Ezért
prímtényezős felbontásába vagy sem. Ezért 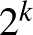 féleképpen válaszhatjuk ki az
féleképpen válaszhatjuk ki az 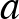 értékét. Most már ki is számolhatjuk az
értékét. Most már ki is számolhatjuk az 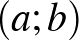 számpárok számát:
számpárok számát:
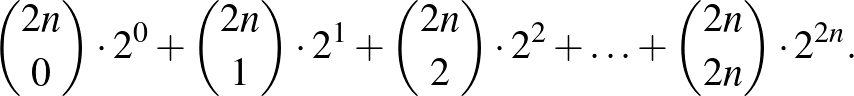
Ez az összeg kissé ijesztő lehet (pláne, ha az ember életében először egy ötórás verseny közepén találkozik vele). Alaposabban megnézve azonban azt láthatjuk, hogy a binomiális tétel segítségével a hosszú összeg megszelidíthető, hiszen értéke éppen 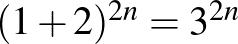 .
.
Most nézzük meg, mit kell ebből kivonni. Ha 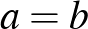 , akkor az ilyen számpárok száma éppen az összes lehetséges
, akkor az ilyen számpárok száma éppen az összes lehetséges 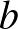 érték száma, tehát
érték száma, tehát 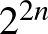 . Most felírhatjuk a feladat szövegében keresett számpárok számát, ez
. Most felírhatjuk a feladat szövegében keresett számpárok számát, ez 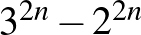 . Azt kell bebizonyítani, hogy ez minden
. Azt kell bebizonyítani, hogy ez minden 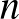 esetén osztható 5-tel. A középiskolai tananyagban szerepel, hogyan lehet szorzattá alakítani az
esetén osztható 5-tel. A középiskolai tananyagban szerepel, hogyan lehet szorzattá alakítani az 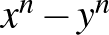 alakú kifejezéseket. Ennek segítségével
alakú kifejezéseket. Ennek segítségével
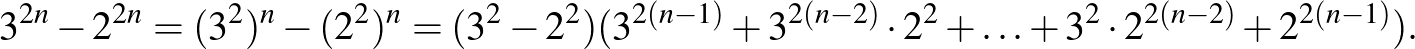
A szorzat első tényezője 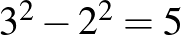 , ezzel az állítást beláttuk.
, ezzel az állítást beláttuk.
Azok a versenyzők, akik a binomiális tétel alkalmazhatóságát nem vették észre, bizony gyakran jóval hosszadalmasabb érvelésre kényszerültek. Most, hogy egy megoldást már végignéztünk, érdemes kicsit visszatekinteni. Ezt ajánlom mind tanároknak, mind diákoknak! Ne hagyjuk ott a feladatot, amint kész a megoldás! Járjuk végig újra az utat, elemezzük, mit is csináltunk! A feladat szövegének megértése, a feltételek szerinti számpár keresése oszthatósági probléma. A megfelelő számpárok leszámolása kombinatorikus lépést igényel. Végül következik a számpárok számának öttel való oszthatósági vizsgálata, melyet így is elvégezhetünk: 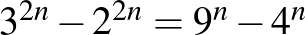 . Mivel 9 és 4 ötös maradéka megegyezik, ezért azonos hatványaiknak az ötös maradéka is megegyezik, tehát különbségük osztható öttel. A kongruenciák nyelvén:
. Mivel 9 és 4 ötös maradéka megegyezik, ezért azonos hatványaiknak az ötös maradéka is megegyezik, tehát különbségük osztható öttel. A kongruenciák nyelvén: 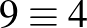 (mod 5), tehát
(mod 5), tehát 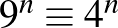 (mod5), azaz
(mod5), azaz 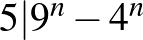 . Az alábbi, második megoldás a kombinatorikus lépést másként kezeli.
. Az alábbi, második megoldás a kombinatorikus lépést másként kezeli.
Második megoldás (ez szerepelt a javítási útmutatóban):
Legyen 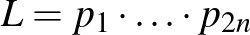 , a
, a 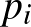 prím kitevője legyen
prím kitevője legyen 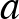 -ban
-ban 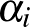 ,
, 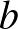 -ben
-ben 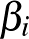 . Amennyiben az
. Amennyiben az 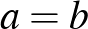 eseteket is megszámoljuk, akkor minden prím esetén a feladat feltétele miatt a lehetséges
eseteket is megszámoljuk, akkor minden prím esetén a feladat feltétele miatt a lehetséges 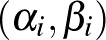 párok: (0,0), (0,1) és (1,1). Tehát három lehetőség van. Mivel
párok: (0,0), (0,1) és (1,1). Tehát három lehetőség van. Mivel 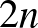 prím van és a kitevőket egymástól függetlenül választhatjuk, ekkor az
prím van és a kitevőket egymástól függetlenül választhatjuk, ekkor az 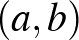 párok száma
párok száma 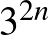 . Ebből ki kell vonni azon párok számát, ahol
. Ebből ki kell vonni azon párok számát, ahol 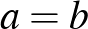 . Minden
. Minden 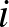 -re
-re 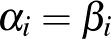 és értéke 0, vagy 1. Tehát két lehetőség van. Most is a kitevőket egymástól függetlenül választhatjuk, így az
és értéke 0, vagy 1. Tehát két lehetőség van. Most is a kitevőket egymástól függetlenül választhatjuk, így az 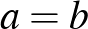 párok száma
párok száma 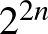 . Már meg is kaptuk a keresett számpárok számát:
. Már meg is kaptuk a keresett számpárok számát: 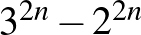 . Innen a befejezés az első megoldás végén található szorzattá alakítással adódik.
. Innen a befejezés az első megoldás végén található szorzattá alakítással adódik.
Az egyik versenyző ezt a gondolatmenetet a következő módon szemléltette. Tekintsük 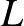 összes prímosztójának
összes prímosztójának 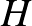 halmazát. Ennek egy
halmazát. Ennek egy 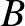 részhalmaza lesz a
részhalmaza lesz a 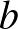 -ben szereplő prímek, majd ezen
-ben szereplő prímek, majd ezen 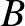 halmazon belül,
halmazon belül, 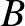 -nek részhalmazaként kapjuk az
-nek részhalmazaként kapjuk az 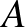 halmazt. Ez utóbbiban legyenek az
halmazt. Ez utóbbiban legyenek az 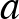 -ban szereplő prímek. Ábránk így néz ki:
-ban szereplő prímek. Ábránk így néz ki:
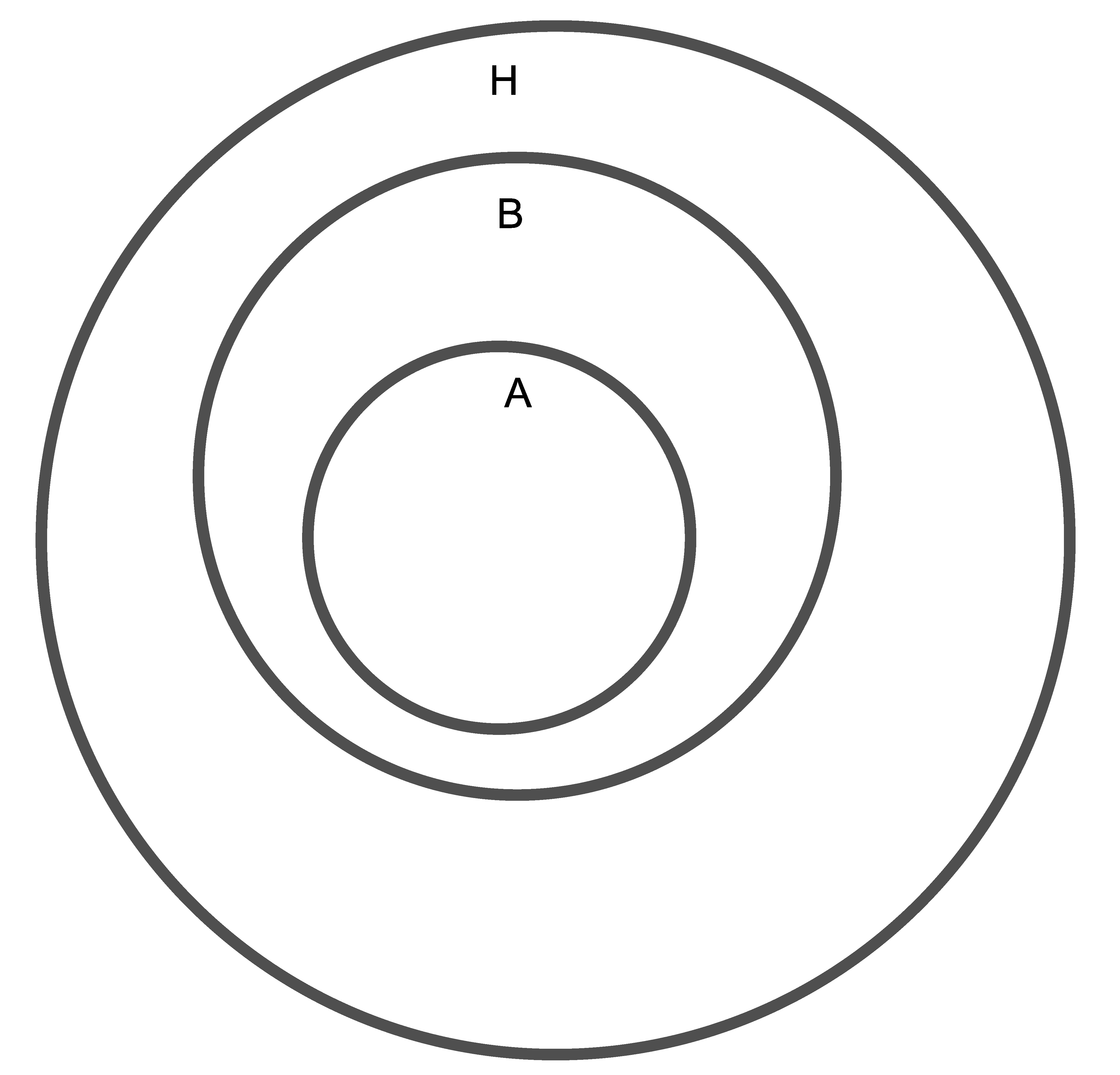
Ha 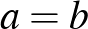 is lehet, akkor minden egyes prímről eldönthetjük, hogy az ábrán szereplő három rész melyikébe kerül, a legbelső körbe, a középső gyűrűbe vagy a szélső gyűrűbe. Ebből adódik a
is lehet, akkor minden egyes prímről eldönthetjük, hogy az ábrán szereplő három rész melyikébe kerül, a legbelső körbe, a középső gyűrűbe vagy a szélső gyűrűbe. Ebből adódik a 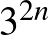 . Azon számpárok esetében, ahol
. Azon számpárok esetében, ahol 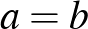 , a prím a középsőbe nem kerülhet, így ezek száma
, a prím a középsőbe nem kerülhet, így ezek száma 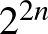 .
.
Harmadik megoldás:
A gyakorlott problémamegoldó számára a feladat szövegének első mondata egy meghívást jelenthet arra, oldjuk meg indukcióval a feladatot. A kezdő lépést már korábban elvégeztük, 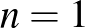 esetén igazoltuk az állítást. Most következhet az indukciós lépés. Feltesszük, hogy az állítás igaz
esetén igazoltuk az állítást. Most következhet az indukciós lépés. Feltesszük, hogy az állítás igaz 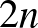 -re és ennek segítségével bebizonyítjuk
-re és ennek segítségével bebizonyítjuk 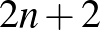 -re. Tekintsünk egy olyan
-re. Tekintsünk egy olyan 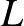 számot, aminek
számot, aminek 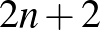 különböző prímosztója van, ezek küzöl legyen a két legnagyobb
különböző prímosztója van, ezek küzöl legyen a két legnagyobb 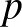 és
és 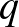 . Tekintsük az
. Tekintsük az 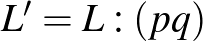 számot, ennek
számot, ennek 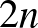 prímosztója van, alkalmazható rá az indukciós feltétel. Soroljuk fel
prímosztója van, alkalmazható rá az indukciós feltétel. Soroljuk fel 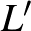 összes megfelelő
összes megfelelő 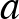 és
és 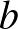 számpárját, legyen ezek száma
számpárját, legyen ezek száma 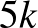 . Az
. Az 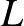 megfelelő számpárjait úgy vizsgáljuk, hogy az
megfelelő számpárjait úgy vizsgáljuk, hogy az 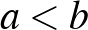 feltétel már az
feltétel már az 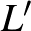 -ben szereplő prímeket tekintve teljesül vagy nem. Az első esetben megnézzük, hogy
-ben szereplő prímeket tekintve teljesül vagy nem. Az első esetben megnézzük, hogy 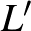 számpárjait megszorozzuk-e a két legnagyobb prímmel. Jó párok lesznek
számpárjait megszorozzuk-e a két legnagyobb prímmel. Jó párok lesznek 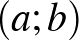 ,
, 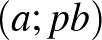 ,
, 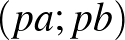 ;
; 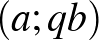 ,
, 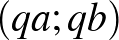 ,
, 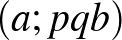 ,
, 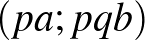 ,
, 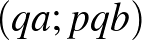 ,
, 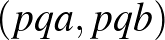 számpárok, ezek száma
számpárok, ezek száma 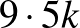 , ami osztható öttel. A második esetben meg kell számolnunk azokat a párokat, ahol
, ami osztható öttel. A második esetben meg kell számolnunk azokat a párokat, ahol 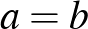 .
. 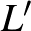 -nek egy tetszőleges osztóját választjuk, legyen ez
-nek egy tetszőleges osztóját választjuk, legyen ez 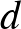 . Ebből
. Ebből 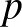 és
és 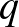 segítségével a következő számpárok készíthetők:
segítségével a következő számpárok készíthetők: 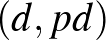 ,
, 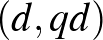 ,
, 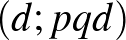 ,
, 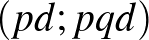 ,
, 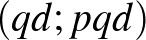 . Mivel minden
. Mivel minden 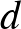 esetén ötféle új számpár készíthető, ezért itt is öttel osztható lesz a megfelelő számpárok száma. Megszámoltuk
esetén ötféle új számpár készíthető, ezért itt is öttel osztható lesz a megfelelő számpárok száma. Megszámoltuk 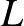 összes megfelelő számpárját és ez két öttel osztható szám összegeként adódótt, tehát az idukciós állítást bizonyítottuk.
összes megfelelő számpárját és ez két öttel osztható szám összegeként adódótt, tehát az idukciós állítást bizonyítottuk.
Megjegyzésként hozzáfűzném, hogy a feladat megoldására „rímel” egy korábbi OKTV példa. Az 1995-ös év II. kategóriás döntőjének első feladata a következő volt:
Adott a 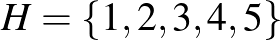 halmaz. Készítsük el ennek összes részhalmazát. Vegyük egyenként az így kapott halmazokat, és mindegyiknek minden részhalmazát írjuk fel külön-külön egy-egy piros cédulára. Így a piros cédulák között lehetnek olyanok, amelyekre ugyanaz a részhalmaz van felírva, de mindet megtartjuk. Vegyük most sorra egyesével a piros cédulákat, és a rajtuk levő halmaz minden részhalmazát külön-külön felírjuk egy-egy fehér cédulára. Vegyük végül sorra a fehér cédulákat, és a rajtuk levő halmaz minden részhalmazát külön-külön felírjuk egy-egy zöld cédulára. Hány zöld cédulát kell így felhasználnunk?
halmaz. Készítsük el ennek összes részhalmazát. Vegyük egyenként az így kapott halmazokat, és mindegyiknek minden részhalmazát írjuk fel külön-külön egy-egy piros cédulára. Így a piros cédulák között lehetnek olyanok, amelyekre ugyanaz a részhalmaz van felírva, de mindet megtartjuk. Vegyük most sorra egyesével a piros cédulákat, és a rajtuk levő halmaz minden részhalmazát külön-külön felírjuk egy-egy fehér cédulára. Vegyük végül sorra a fehér cédulákat, és a rajtuk levő halmaz minden részhalmazát külön-külön felírjuk egy-egy zöld cédulára. Hány zöld cédulát kell így felhasználnunk?
A két feladat hasonló vonása az, hogyan számoljuk meg egy 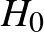 halmaz olyan
halmaz olyan 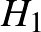 ,
, 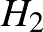 , ...,
, ..., 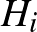 részhalmazláncainak számát, amelyekre
részhalmazláncainak számát, amelyekre 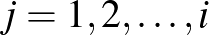 esetén a
esetén a 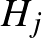 halmaz részhalmaza
halmaz részhalmaza 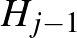 -nek. Az idei feladatban
-nek. Az idei feladatban 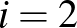 , a 95-ös példában
, a 95-ös példában 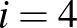 szerepelt. A részhalmazláncok száma
szerepelt. A részhalmazláncok száma 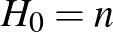 esetén
esetén 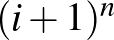 , hiszen
, hiszen 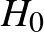 mind az
mind az 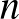 darab eleménél egymástól függetlenül eldönthetjük, melyik a legnagyobb
darab eleménél egymástól függetlenül eldönthetjük, melyik a legnagyobb 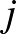 index, amely
index, amely 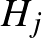 -ben az elem még szerepel. Itt most
-ben az elem még szerepel. Itt most 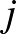 értéke 0 és
értéke 0 és 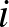 közt bármi lehet, azaz
közt bármi lehet, azaz 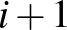 lehetőség van.
lehetőség van.
Remélem a tehetséggondozásban munkálkodó kollégáknak és az érdeklődő diákoknak egyaránt hasznos dolgokra sikerült rávilágítani ezzel a kis összeállítással.









