Előzmények
A 9. osztályos matematika tanórán egy érdekes problémakört érintettünk. Geometriából éppen a síkbeli alapszerkesztéseket tekintettük át, az ezekhez kötődő kérdések két (alap)feladat tárgyalásakor vetődtek fel. A továbbiakban először ismertetjük a két (nagyon egyszerű) alapfeladat (az 1. és a 2. feladat) egy lehetséges megoldását és a kapcsolódó tanulói kérdést, majd megadjuk a felvetett problémakör néhány eredményét.
Az eszközkorlátozott szerkesztések témaköre önállóan is érdekes. Általában nem igényel mélyebb előismereteket, ezért a tanulók kedvelni szokták, a dinamikus geometriai szoftverekkel pedig maga a szerkesztés technikai végrehajtása sem túl fáradságos.
1. feladat: Adott egy ![]() egyenes és rajta kívül egy
egyenes és rajta kívül egy ![]() pont. Szerkesszünk a
pont. Szerkesszünk a ![]() pontból merőlegest az
pontból merőlegest az ![]() egyenesre!
egyenesre!
Megoldás:
![]() :
: ![]() középpontú
középpontú ![]() kört rajzolunk úgy, hogy a kör sugara,
kört rajzolunk úgy, hogy a kör sugara, ![]() nagyobb legyen a
nagyobb legyen a ![]() és
és ![]() távolságánál.
távolságánál. ![]() és
és ![]() metszéspontjait jelölje
metszéspontjait jelölje ![]() és
és ![]() .
.
![]() :
: ![]() középpontú
középpontú ![]() kört rajzolunk „elég nagy”
kört rajzolunk „elég nagy” ![]() sugárral (azaz a kör sugarára
sugárral (azaz a kör sugarára ![]() teljesüljön).
teljesüljön).
![]() :
: ![]() középpontú
középpontú ![]() kört szerkesztünk ugyanakkora
kört szerkesztünk ugyanakkora ![]() sugárral.
sugárral.
![]() :
: ![]() és
és ![]() egyik metszéspontját
egyik metszéspontját ![]() -vel összekötve megkapjuk a kért
-vel összekötve megkapjuk a kért ![]() egyenest (
egyenest (![]() az
az ![]() szakasz felező merőlegese).
szakasz felező merőlegese).

2. feladat: Adott egy ![]() egyenes és rajta kívül egy
egyenes és rajta kívül egy ![]() pont. Tükrözzük a
pont. Tükrözzük a ![]() pontot az
pontot az ![]() egyenesre!
egyenesre!
Megoldás:
![]() . Felhasználjuk az 1. feladat megoldását, megszerkesztjük az
. Felhasználjuk az 1. feladat megoldását, megszerkesztjük az ![]() -re merőleges,
-re merőleges, ![]() -n átmenő
-n átmenő ![]() egyenest.
egyenest.
![]() . Jelölje
. Jelölje ![]() az
az ![]() és
és ![]() egyenesek metszéspontját. Felvesszük a
egyenesek metszéspontját. Felvesszük a ![]() középpontú,
középpontú, ![]() sugarú
sugarú ![]() kört.
kört.
![]() .
. ![]() és
és ![]() egymást
egymást ![]() -ben és
-ben és ![]() -ben metszik, a
-ben metszik, a ![]() pont keresett tükörképe
pont keresett tükörképe ![]() .
.
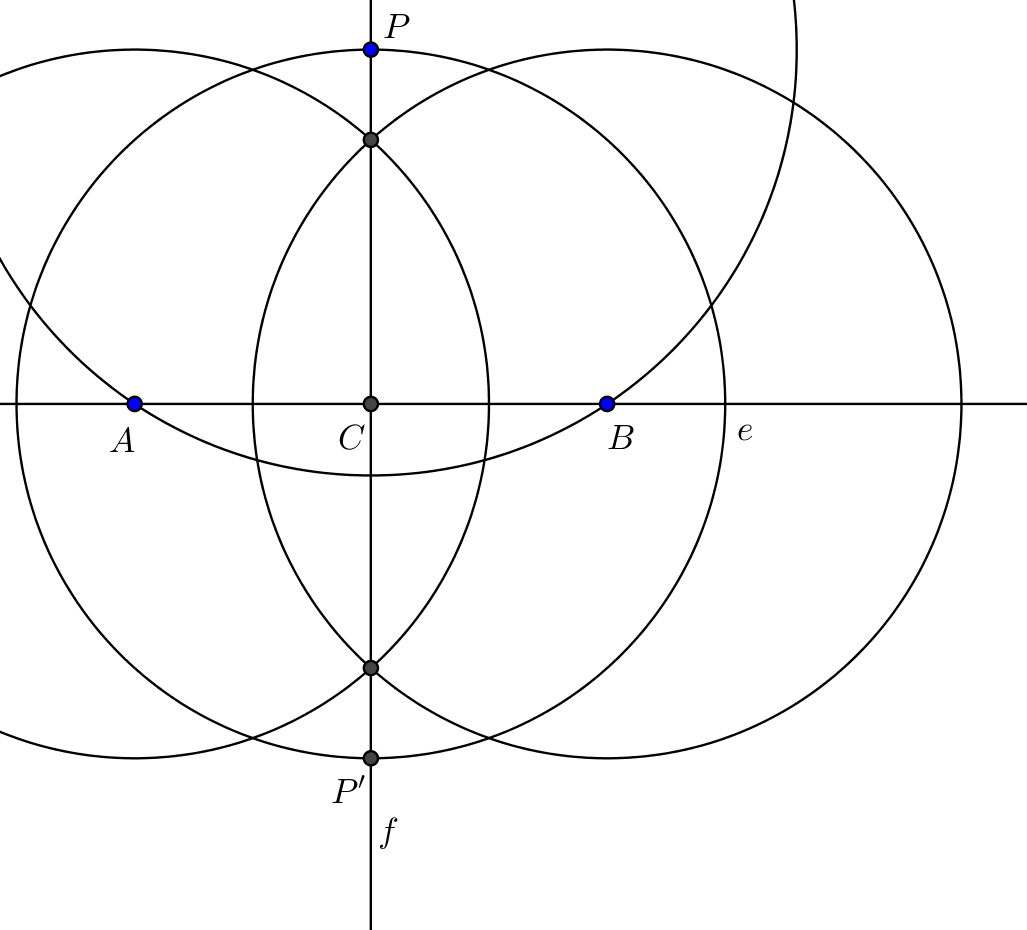
Ebben a megoldásban a ![]() pont tengelyes tükörképének megszerkesztéséhez 4 kört vettünk fel.
pont tengelyes tükörképének megszerkesztéséhez 4 kört vettünk fel.
Természetes módon adódik a kérdés: el lehet-e végezni a szerkesztést ügyesebben, kevesebb kör segítségével?
Három körrel szinte minden tanuló tudta a megoldást, két körrel már némi kreativitásra is szükség volt.
Ez a két feladat vezetett a további kérdésfeltevésekre:
3. feladat: Adott egy ![]() egyenes és rajta kívül egy
egyenes és rajta kívül egy ![]() pont. Tükrözzük a
pont. Tükrözzük a ![]() pontot az
pontot az ![]() egyenesre úgy, hogy a szerkesztéshez csak három kört rajzolhatunk!
egyenesre úgy, hogy a szerkesztéshez csak három kört rajzolhatunk!
Megoldás:
Az 1. feladat megoldásának szerkesztését annyiban módosítjuk, hogy a ![]() ,
, ![]() és
és ![]() körök sugara egyenlő legyen. Ekkor
körök sugara egyenlő legyen. Ekkor ![]() és
és ![]() egyik metszéspontja
egyik metszéspontja ![]() , míg a másik metszéspontja
, míg a másik metszéspontja ![]() , ami
, ami ![]() tükörképe
tükörképe ![]() -re. (
-re. (![]() rombusz.)
rombusz.)

4. feladat: Adott egy ![]() egyenes és rajta kívül egy
egyenes és rajta kívül egy ![]() pont. Tükrözzük a
pont. Tükrözzük a ![]() pontot az
pontot az ![]() egyenesre úgy, hogy csak két kört szerkeszthetünk!
egyenesre úgy, hogy csak két kört szerkeszthetünk!
Megoldás:
![]() . Legyen
. Legyen ![]() az
az ![]() egyenes tetszőleges pontja. Felvesszük az
egyenes tetszőleges pontja. Felvesszük az ![]() középpontú,
középpontú, ![]() sugarú
sugarú ![]() kört.
kört.
![]() . Hasonlóan, ha
. Hasonlóan, ha ![]() az
az ![]() egyenes egy (
egyenes egy (![]() -tól különböző) tetszőleges pontja, akkor megrajzoljuk a
-tól különböző) tetszőleges pontja, akkor megrajzoljuk a ![]() középpontú,
középpontú, ![]() sugarú
sugarú ![]() kört.
kört.
![]() . Ekkor
. Ekkor ![]() és
és ![]()
![]() -től különböző metszéspontja
-től különböző metszéspontja ![]() , ami
, ami ![]() tükörképe
tükörképe ![]() -re.
-re.
Indoklásul arra hivatkozhatunk, hogy ![]() deltoid, és ennek
deltoid, és ennek ![]() átlóját az
átlóját az ![]() átló merőlegesen felezi.
átló merőlegesen felezi.

Ezután következett a nehéz kérdés: vajon a szerkesztés (![]() tükrözése
tükrözése ![]() -re) elvégezhető-e egyetlen kör felvételével?
-re) elvégezhető-e egyetlen kör felvételével?
Hasonló, korlátozott szerkesztésekkel kapcsolatos kérdések a 11. osztályos tanórán és szakkörön is felvetődtek. A továbbiakban ezekből a kérdésekből és a rájuk adott válaszokból gyűjtöttünk össze néhányat.
Pont tükrözése egyenesre egyetlen kör felhasználásával
Először segédfeladatként ![]() -ből merőlegest szerkesztünk.
-ből merőlegest szerkesztünk.
5. feladat: Adott egy ![]() egyenes és rajta kívül egy
egyenes és rajta kívül egy ![]() pont. Szerkesszünk a
pont. Szerkesszünk a ![]() pontból merőlegest az
pontból merőlegest az ![]() egyenesre úgy, hogy a szerkesztéshez csak egyetlen kört rajzolhatunk!
egyenesre úgy, hogy a szerkesztéshez csak egyetlen kört rajzolhatunk!
Megoldás:
![]() . Kijelölünk egy
. Kijelölünk egy ![]() pontot ez
pontot ez ![]() egyenesen, és az ábra szerint felveszünk egy
egyenesen, és az ábra szerint felveszünk egy ![]() kört. A kör
kört. A kör ![]() és
és ![]() pontokban metszi az egyenest. (A kör mindig felvehető úgy, hogy
pontokban metszi az egyenest. (A kör mindig felvehető úgy, hogy ![]() körön kívüli pont legyen, és
körön kívüli pont legyen, és ![]() -re vonatkozó merőleges vetülete
-re vonatkozó merőleges vetülete ![]() és
és ![]() közé essen.) Ezek után már csak vonalzót használunk.
közé essen.) Ezek után már csak vonalzót használunk.
![]() . Meghúzzuk a
. Meghúzzuk a ![]() egyenest, ez
egyenest, ez ![]() -t
-t ![]() -ben metszi.
-ben metszi.
![]() . Hasonlóan a
. Hasonlóan a ![]() egyenes
egyenes ![]() -t
-t ![]() -ben metszi.
-ben metszi.
![]() . Felvesszük a
. Felvesszük a ![]() egyenest. Thalész tétele miatt ez merőleges
egyenest. Thalész tétele miatt ez merőleges ![]() -re.
-re.
![]() . Felvesszük az
. Felvesszük az ![]() egyenest. Thalész tétele miatt ez
egyenest. Thalész tétele miatt ez ![]() -re merőleges;
-re merőleges; ![]() és
és ![]() metszéspontját jelölje
metszéspontját jelölje ![]() .
.
![]() . A
. A ![]() egyenes lesz a feladat megoldása. Ugyanis
egyenes lesz a feladat megoldása. Ugyanis ![]() az
az ![]() háromszög
háromszög ![]() és
és ![]() magasságainak metszéspontja, azaz magasságpont; akkor pedig
magasságainak metszéspontja, azaz magasságpont; akkor pedig ![]() is magasságvonal a háromszögben.
is magasságvonal a háromszögben.

Megjegyzések: A szerkesztés akkor is végrehajtható, ha ![]() a körön belüli pont (ekkor
a körön belüli pont (ekkor ![]() és
és ![]() szerepet cserél).
szerepet cserél).
Sőt a szerkesztés akkor is „működik”, ha ![]() tompaszögű háromszög (például
tompaszögű háromszög (például ![]() merőleges vetülete az
merőleges vetülete az ![]() szakasz
szakasz ![]() -n túli meghosszabbítására esik), a szerkesztési lépések ugyanazok maradnak.
-n túli meghosszabbítására esik), a szerkesztési lépések ugyanazok maradnak.

6. feladat: Adott egy ![]() egyenes és rajta kívül egy
egyenes és rajta kívül egy ![]() pont. Tükrözzük a
pont. Tükrözzük a ![]() pontot az
pontot az ![]() egyenesre úgy, hogy a szerkesztéshez csak egyetlen kört rajzolhatunk!
egyenesre úgy, hogy a szerkesztéshez csak egyetlen kört rajzolhatunk!
Első megoldás (Korinek Ádám 11.a):

![]() . Az 5. feladat alapján
. Az 5. feladat alapján ![]() -ből az
-ből az ![]() (
(![]() ) egyenesre megszerkesztjük az
) egyenesre megszerkesztjük az ![]() merőlegest. Ez a
merőlegest. Ez a ![]() kört
kört ![]() -ben és
-ben és ![]() -ben metszi.
-ben metszi.
![]() . Felvesszük a
. Felvesszük a ![]() és
és ![]() egyeneseket, ezek
egyeneseket, ezek ![]() -t
-t ![]() -ben, illetve
-ben, illetve ![]() -ben metszik.
-ben metszik.
![]() . Felvesszük a
. Felvesszük a ![]() és
és ![]() egyeneseket, ezek
egyeneseket, ezek ![]() -t
-t ![]() -ben,
-ben, ![]() -t
-t ![]() -ban metszik.
-ban metszik.
![]() . Felvesszük a
. Felvesszük a ![]() egyenest, ez az
egyenest, ez az ![]() pontban metszi
pontban metszi ![]() -t.
-t.
![]() . Végül
. Végül ![]() és
és ![]() metszéspontja legyen
metszéspontja legyen ![]() , ez a keresett
, ez a keresett ![]() pont,
pont, ![]() tükörképe.
tükörképe.
Indoklás: ![]() és
és ![]() szimmetrikus helyzetű
szimmetrikus helyzetű ![]() -re, így
-re, így ![]() is szimmetrikus háromszög.
is szimmetrikus háromszög.
Megjegyzések: Általános módszert kaptunk: ![]() tengelyes tükrözéséhez elegendő egy
tengelyes tükrözéséhez elegendő egy ![]() és
és ![]() tükörkép-pontpár megszerkesztése (a tengelyes szimmetria közvetítő szerepe).
tükörkép-pontpár megszerkesztése (a tengelyes szimmetria közvetítő szerepe).
Problémát jelenthet, ha ![]() párhuzamos
párhuzamos ![]() -vel (
-vel (![]() nem áll elő). Azonban a módszerünk alapján már
nem áll elő). Azonban a módszerünk alapján már ![]() és
és ![]() tükrös helyzetűek, a szerkesztés velük is befejezhető (a 3. és 4. szerkesztési lépés felesleges). Gyorsabban célt érünk tehát, ha a
tükrös helyzetűek, a szerkesztés velük is befejezhető (a 3. és 4. szerkesztési lépés felesleges). Gyorsabban célt érünk tehát, ha a ![]() és
és ![]() metszéspontját vesszük fel (
metszéspontját vesszük fel (![]() ), ekkor
), ekkor ![]() és
és ![]() metszéspontja jelöli ki
metszéspontja jelöli ki ![]() -t.
-t.
A két lehetőség közül az egyik biztosan végrehajtható, ![]() vagy
vagy ![]() valamelyike mindig létezik.
valamelyike mindig létezik.
Második megoldás (Szepessy Hajnalka 11.a):

![]() .
. ![]() középpontú,
középpontú, ![]() -n átmenő
-n átmenő ![]() kört rajzolunk. A kör
kört rajzolunk. A kör ![]() és
és ![]() pontokban metszi
pontokban metszi ![]() -t (
-t (![]() ).
).
![]() . Az 5. feladat alapján az
. Az 5. feladat alapján az ![]() egyenesre tetszőleges pontból
egyenesre tetszőleges pontból ![]() merőlegest szerkesztünk evvel a
merőlegest szerkesztünk evvel a ![]() körrel. A kört
körrel. A kört ![]() metszi
metszi ![]() -ben és
-ben és ![]() -ben.
-ben.
![]() .
. ![]() metszi
metszi ![]() -t
-t ![]() -ben.
-ben.
![]() .
. ![]() metszi
metszi ![]() -t
-t ![]() -ban. Készen vagyunk:
-ban. Készen vagyunk: ![]() .
.
Megjegyzések: Ebben a megoldásban is a pontpárok tengelyes szimmetriáját használtuk fel (és a kör közvetítő szerepét).
Harmadik megoldás (Kotán Tamás 11.a):

![]() .
. ![]() középpontú,
középpontú, ![]() -n átmenő
-n átmenő ![]() kört rajzolunk. A kör
kört rajzolunk. A kör ![]() és
és ![]() pontokban metszi
pontokban metszi ![]() -t (
-t (![]() ).
).
![]() . Az 5. feladat alapján az
. Az 5. feladat alapján az ![]() egyenesre tetszőleges pontból
egyenesre tetszőleges pontból ![]() merőlegest szerkesztünk a
merőlegest szerkesztünk a ![]() körrel. A kört
körrel. A kört ![]() metszi
metszi ![]() -ben és
-ben és ![]() -ben, az
-ben, az ![]() egyenest
egyenest ![]() -ben.
-ben.
![]() .
. ![]() metszi
metszi ![]() -t
-t ![]() -ben.
-ben.
![]() .
. ![]() metszi
metszi ![]() -et
-et ![]() -ben.
-ben.
![]() .
. ![]() metszi
metszi ![]() -t
-t ![]() -ban.
-ban.
Állítás: ![]() .
.
Bizonyítás (Dobos Sándor): ![]() húrnégyszög, mert
húrnégyszög, mert ![]() . (
. (![]() .) Ezért
.) Ezért ![]() (kerületi szögek). Ekkor a
(kerületi szögek). Ekkor a ![]() körben a szögekhez tartozó ívek és a húrok is egyenlők:
körben a szögekhez tartozó ívek és a húrok is egyenlők: ![]() . Vagyis
. Vagyis ![]() valóban
valóban ![]() tükörképe
tükörképe ![]() -re.
-re.
Negyedik megoldás (Kotán Tamás 11.a):

![]() .
. ![]() középpontú,
középpontú, ![]() -n átmenő
-n átmenő ![]() kört rajzolunk. A kör
kört rajzolunk. A kör ![]() és
és ![]() pontokban metszi
pontokban metszi ![]() -t (
-t (![]() ).
).
![]() . Az 5. feladat alapján az
. Az 5. feladat alapján az ![]() egyenesre tetszőleges pontból
egyenesre tetszőleges pontból ![]() merőlegest szerkesztünk a
merőlegest szerkesztünk a ![]() körrel. A kört
körrel. A kört ![]() metszi
metszi ![]() -ben és
-ben és ![]() -ben.
-ben.
![]() .
. ![]() metszi
metszi ![]() -t
-t ![]() -ben.
-ben.
![]() .
. ![]() metszi
metszi ![]() -t
-t ![]() -ban.
-ban.
Állítás: ![]() .
.
Bizonyításként arra hivatkozhatunk, hogy ![]() az
az ![]() -re tengelyesen szimmetrikus alakzat, azaz húrtrapéz.
-re tengelyesen szimmetrikus alakzat, azaz húrtrapéz.
Pont tükrözése egyenesre egyetlen kör felhasználásával – de a kört más rajzolja meg
Az eddigi szerkesztésekben megszorító feltétel volt, hogy csak egyetlen kör rajzolható. Igaz, ezt úgy vehettük fel, ahogy szükségünk volt rá. Érdekes kérdés vetődött fel az órákon, további szigorításként: mi a helyzet akkor, ha (az egyetlen) kört más rajzolja meg? Azaz, ha a kör, a ![]() pont és az egyenes helyzete már rögzített.
pont és az egyenes helyzete már rögzített.
Ha az egyenes a kör átmérője, és a ![]() pont a körön van, akkor például a fenti második megoldás most is alkalmazható.
pont a körön van, akkor például a fenti második megoldás most is alkalmazható.
7. feladat: Adott egy ![]() egyenes és egy kör, amelynek
egyenes és egy kör, amelynek ![]() középpontja az egyenesen van. Továbbá legyen az adott
középpontja az egyenesen van. Továbbá legyen az adott ![]() pont például a körön kívül. Tükrözzük a
pont például a körön kívül. Tükrözzük a ![]() pontot az
pontot az ![]() egyenesre úgy, hogy további kört már nem rajzolhatunk!
egyenesre úgy, hogy további kört már nem rajzolhatunk!
Megoldás:

A ![]() kör és
kör és ![]() két metszéspontja legyen
két metszéspontja legyen ![]() és
és ![]() .
.
![]() . Az 5. feladat alapján az
. Az 5. feladat alapján az ![]() egyenesre tetszőleges pontból
egyenesre tetszőleges pontból ![]() merőlegest szerkesztünk, ez a kört metszi
merőlegest szerkesztünk, ez a kört metszi ![]() -ben és
-ben és ![]() -ben.
-ben.
![]() .
. ![]() metszi
metszi ![]() -t
-t ![]() -ben.
-ben.
![]() . Felvesszük az
. Felvesszük az ![]() egyenest.
egyenest.
![]() .
. ![]() -ből merőlegest húzunk
-ből merőlegest húzunk ![]() -re, ez kimetszi
-re, ez kimetszi ![]() -ből a keresett
-ből a keresett ![]() pontot.
pontot.
Megjegyzések: Ismét az ábra tengelyes szimmetriáját használtuk ki, csak most a külső ![]() pont miatt két merőlegest kellett szerkesztenünk. De a szerkesztés ugyanígy lépésenként végrehajtható akkor is, ha a
pont miatt két merőlegest kellett szerkesztenünk. De a szerkesztés ugyanígy lépésenként végrehajtható akkor is, ha a ![]() pont a körön belül van.
pont a körön belül van.
A kör középpontjának szerepe
Nehezebb a szerkesztési feladat akkor, ha az ![]() egyenes nem átmérője az adott körnek. Ekkor új ötletre van szükség (ez lesz a trapéztrükk).
egyenes nem átmérője az adott körnek. Ekkor új ötletre van szükség (ez lesz a trapéztrükk).
Először figyeljük meg, hogy az eddigi szerkesztések során egyedül a 6. feladat első megoldása használta fel az ![]() pontot, az adott kör középpontját. A többi megoldásban
pontot, az adott kör középpontját. A többi megoldásban ![]() -ra nem volt szükség, a körközéppont ismerete nélkül is végrehajthatók voltak a szerkesztések.
-ra nem volt szükség, a körközéppont ismerete nélkül is végrehajthatók voltak a szerkesztések.
A továbbiakban egy olyan módszert mutatunk, amely három ekvidisztáns helyzetű pont esetén alkalmazható. (![]() ,
, ![]() ,
, ![]() egy egyenesen lévő pontok ekvidisztáns helyzetűek, ha például
egy egyenesen lévő pontok ekvidisztáns helyzetűek, ha például ![]() .) Ha a korábbi szerkesztésekben ismerjük az
.) Ha a korábbi szerkesztésekben ismerjük az ![]() pontot, akkor ennek alapján további megoldási lehetőségekhez jutunk, mert ekkor az adott
pontot, akkor ennek alapján további megoldási lehetőségekhez jutunk, mert ekkor az adott ![]() ,
, ![]() ,
, ![]() pontok ekvidisztáns helyzetűek.
pontok ekvidisztáns helyzetűek.
8. feladat (segédfeladat – trapéztrükk): Adott az ![]() egyenesen három ekvidisztáns helyzetű
egyenesen három ekvidisztáns helyzetű ![]() ,
, ![]() ,
, ![]() pont (
pont (![]() ). Szerkesztendő csak vonalzóval külső
). Szerkesztendő csak vonalzóval külső ![]() ponton keresztül
ponton keresztül ![]() -vel párhuzamos egyenes.
-vel párhuzamos egyenes.
Megoldás:

![]() . Az
. Az ![]() egyenesen felveszünk egy tetszőleges
egyenesen felveszünk egy tetszőleges ![]() pontot.
pontot.
![]() . Felvesszük a
. Felvesszük a ![]() egyenest.
egyenest.
![]() . Felvesszük a
. Felvesszük a ![]() egyenest, ez metszi
egyenest, ez metszi ![]() -t
-t ![]() -ben.
-ben.
![]() . Meghúzzuk a
. Meghúzzuk a ![]() egyenest.
egyenest.
![]() . Az
. Az ![]() egyenes metszi
egyenes metszi ![]() -t
-t ![]() -ben.
-ben.
Állítás: ![]() párhuzamos
párhuzamos ![]() -vel.
-vel.
Bizonyítás: A trapézok egy ismert tulajdonságát használjuk fel. Bármely ![]() trapézban, ha az átlók
trapézban, ha az átlók ![]() metszéspontján át párhuzamost húzunk az alapokkal, akkor a szárakkal vett
metszéspontján át párhuzamost húzunk az alapokkal, akkor a szárakkal vett ![]() ,
, ![]() metszéspontokra
metszéspontokra ![]() . Emiatt az
. Emiatt az ![]() kiegészítő sháromszög
kiegészítő sháromszög ![]() súlyvonalán rajta van
súlyvonalán rajta van ![]() ; a szerkesztés során ennek a tételnek a megfordítását használtuk fel.
; a szerkesztés során ennek a tételnek a megfordítását használtuk fel.
Alkalmazhatjuk Ceva tételét is az ![]() háromszögben. Az
háromszögben. Az ![]() ,
, ![]() ,
, ![]() transzverzálisok egy ponton mennek át, ezért
transzverzálisok egy ponton mennek át, ezért ![]() . Innen
. Innen ![]() , és a párhuzamos szelők tételének megfordításához ennyi elég,
, és a párhuzamos szelők tételének megfordításához ennyi elég, ![]() és
és ![]() párhuzamosak.
párhuzamosak.
Bevezetünk egy új definíciót: ha egy egyenesen adott három ekvidisztáns helyzetű pont, akkor irányegyenesnek nevezzük. (A trapéztrükkel azt mutattuk meg, hogy külső pontból adott irányegyenessel tudunk párhuzamost szerkeszteni úgy, hogy csak vonalzót használunk.)
A trapéztrükk segítségével a 7. feladat szerkesztését akkor is el tudjuk végezni, ha a ![]() pont az adott körön van.
pont az adott körön van.
9. feladat: Adott egy ![]() egyenes és egy
egyenes és egy ![]() kör, amelynek
kör, amelynek ![]() középpontja az egyenesen van. Továbbá legyen az adott
középpontja az egyenesen van. Továbbá legyen az adott ![]() pont a körön. Tükrözzük a
pont a körön. Tükrözzük a ![]() pontot az
pontot az ![]() egyenesre úgy, hogy további kört már nem rajzolhatunk!
egyenesre úgy, hogy további kört már nem rajzolhatunk!
Megoldás:

A ![]() kör és
kör és ![]() két metszéspontja legyen
két metszéspontja legyen ![]() és
és ![]() . Mivel
. Mivel ![]() ,
, ![]() ,
, ![]() ekvidisztáns pontok, így
ekvidisztáns pontok, így ![]() irányegyenes.
irányegyenes.
![]() .
. ![]() -n keresztül párhuzamost szerkesztünk
-n keresztül párhuzamost szerkesztünk ![]() -vel. Az így kapott
-vel. Az így kapott ![]() egyenes másodszor
egyenes másodszor ![]() -ben metszi
-ben metszi ![]() -t.
-t.
![]() . Felvesszük a
. Felvesszük a ![]() egyenest, ami
egyenest, ami ![]() -ben metszi a kört.
-ben metszi a kört.
Készen vagyunk: Thalész tétele miatt ![]() , így
, így ![]() -nek
-nek ![]() -re vonatkozó tükörképe
-re vonatkozó tükörképe ![]() .
.
Még megoldunk két segédfeladatot.
10. feladat (segédfeladat – párhuzamos húzása): Adott az ![]() középpontú
középpontú ![]() kör. Szerkesszünk csak vonalzó felhasználásával külső
kör. Szerkesszünk csak vonalzó felhasználásával külső ![]() ponton keresztül adott
ponton keresztül adott ![]() egyenessel párhuzamos egyenest!
egyenessel párhuzamos egyenest!
Megoldás:

A feladat tulajdonképpen három ekvidisztáns pont szerkesztése ![]() -re, mert így akkor
-re, mert így akkor ![]() irányegyenes lesz. (És vele párhuzamos egyenes már szerkeszthető a trapéztrükkel.)
irányegyenes lesz. (És vele párhuzamos egyenes már szerkeszthető a trapéztrükkel.)
![]() . Az
. Az ![]() egyenes tetszőleges
egyenes tetszőleges ![]() pontját összekötjük
pontját összekötjük ![]() -val. Az így kapott
-val. Az így kapott ![]() egyenes metszéspontjai
egyenes metszéspontjai ![]() -val
-val ![]() és
és ![]() .
.
![]() .
. ![]() irányegyenes, így az
irányegyenes, így az ![]() egyenes egy
egyenes egy ![]() pontjából párhuzamost húzunk
pontjából párhuzamost húzunk ![]() -fel úgy, hogy az egyenes két pontban metssze
-fel úgy, hogy az egyenes két pontban metssze ![]() -t. A metszéspontokat jelölje
-t. A metszéspontokat jelölje ![]() és
és ![]() .
.
![]() . Az
. Az ![]() egyenes metszi
egyenes metszi ![]() -t
-t ![]() -ben, az
-ben, az ![]() egyenes pedig metszi
egyenes pedig metszi ![]() -t
-t ![]() -ban.
-ban.
![]() . A
. A ![]() egyenes metszi
egyenes metszi ![]() -t
-t ![]() -ben.
-ben.
Állítás: ![]() . Ugyanis
. Ugyanis ![]() téglalap, amelyben
téglalap, amelyben ![]() középvonal, így a három párhuzamos egyenes ekvidisztáns pontokban metszi
középvonal, így a három párhuzamos egyenes ekvidisztáns pontokban metszi ![]() -t.
-t.
Készen vagyunk: ![]() irányegyenes lett, a trapéztrükk alkalmazható.
irányegyenes lett, a trapéztrükk alkalmazható.
![]() . Az
. Az ![]() irányegyenes segítségével megszerkesztjük a
irányegyenes segítségével megszerkesztjük a ![]() -n átmenő párhuzamos egyenest.
-n átmenő párhuzamos egyenest.
Megjegyzés: A 2. lépésben fordítva is eljárhatunk: az ![]() irányegyenessel párhuzamost húzhatunk a kör egy tetszőleges pontján át. Ha például az ábra szerinti
irányegyenessel párhuzamost húzhatunk a kör egy tetszőleges pontján át. Ha például az ábra szerinti ![]() ponton keresztül húzunk párhuzamost, akkor ez kijelöli a
ponton keresztül húzunk párhuzamost, akkor ez kijelöli a ![]() pontot.
pontot.
11. feladat (segédfeladat – ![]() szakasz eltolása): Adott az
szakasz eltolása): Adott az ![]() középpontú
középpontú ![]() kör, valamint az
kör, valamint az ![]() ,
, ![]() ,
, ![]() pontok. Toljuk el az
pontok. Toljuk el az ![]() szakaszt úgy, hogy az
szakaszt úgy, hogy az ![]() pont
pont ![]() -be kerüljön!
-be kerüljön!
Megoldás:
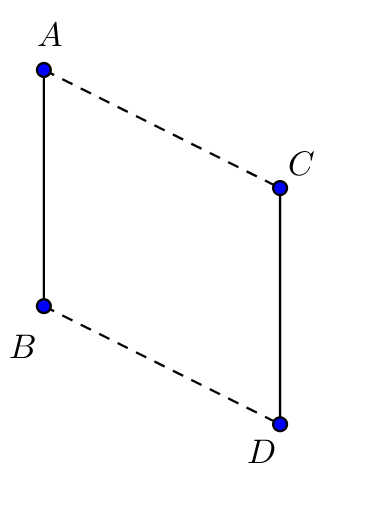
A ![]() pont képét jelölje
pont képét jelölje ![]() .
.
I. eset: Ha ![]() ,
, ![]() ,
, ![]() háromszöget alkot, akkor
háromszöget alkot, akkor ![]() paralelogramma, amelynek szemközti oldalai párhuzamosak.
paralelogramma, amelynek szemközti oldalai párhuzamosak.
Ekkor a 10. segédfeladat alapján párhuzamost húzunk ![]() -vel
-vel ![]() -n keresztül, és
-n keresztül, és ![]() -vel
-vel ![]() -n keresztül. A két egyenes metszéspontja
-n keresztül. A két egyenes metszéspontja ![]() .
.
II. eset: Ha ![]() ,
, ![]() ,
, ![]() egy egyenesbe esik.
egy egyenesbe esik.
Ekkor viszont az egyenesen kívül eső tetszőleges pontba eltolhatjuk az ![]() szakaszt (I. eset). Az így kapott
szakaszt (I. eset). Az így kapott ![]() szakasz és
szakasz és ![]() már nem esik egy egyenesre, alkalmazhatjuk az I. eset szerkesztését: az
már nem esik egy egyenesre, alkalmazhatjuk az I. eset szerkesztését: az ![]() szakaszt eltoljuk úgy, hogy
szakaszt eltoljuk úgy, hogy ![]()
![]() -be kerüljön.
-be kerüljön.
Ha tehát a kör már adott a szerkesztés kezdetekor
A 8., 10. és 11. segédfeladatokkal most már elvégezhetjük a kitűzött szerkesztésünket.
12. feladat: Adott egy egyenes, egy külső ![]() pont és egy
pont és egy ![]() középpontú kör. Tükrözzük a
középpontú kör. Tükrözzük a ![]() pontot az egyenesre úgy, hogy további kört már nem rajzolhatunk!
pontot az egyenesre úgy, hogy további kört már nem rajzolhatunk!
Megoldás:
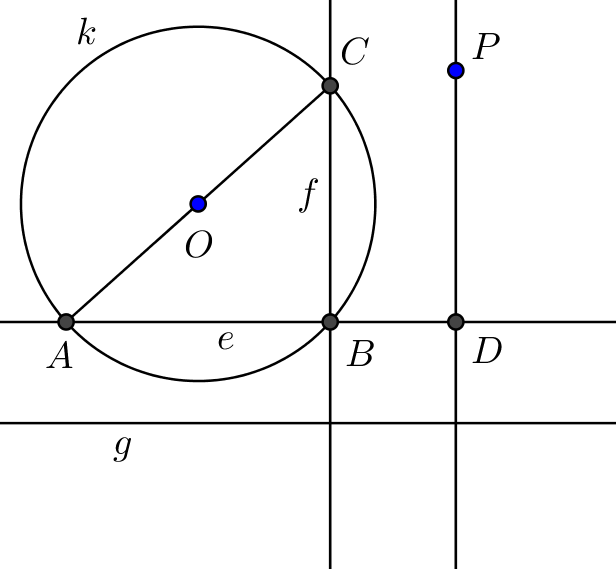
I. eset: Ha az adott ![]() egyenes metszi a
egyenes metszi a ![]() kört, akkor a metszéspontokat jelölje
kört, akkor a metszéspontokat jelölje ![]() ,
, ![]() . (Feltehetjük, hogy
. (Feltehetjük, hogy ![]() nem átmérő; ezt az esetet a fentiekben már részletesen tárgyaltuk.)
nem átmérő; ezt az esetet a fentiekben már részletesen tárgyaltuk.)
![]() . Az
. Az ![]() egyenes metszi
egyenes metszi ![]() -t
-t ![]() -ben.
-ben.
![]() . Felvesszük az
. Felvesszük az ![]() egyenest. Ez merőleges
egyenest. Ez merőleges ![]() -re Thalész tétele miatt.
-re Thalész tétele miatt.
![]() .
. ![]() -ből párhuzamost szerkesztünk
-ből párhuzamost szerkesztünk ![]() -fel (10. segédfeladat), ez az egyenes
-fel (10. segédfeladat), ez az egyenes ![]() -ben metszi
-ben metszi ![]() -t.
-t.
![]() . Végül
. Végül ![]() szakaszt két lépésben eltoljuk úgy, hogy a
szakaszt két lépésben eltoljuk úgy, hogy a ![]() pont
pont ![]() -be kerüljön (11. segédfeladat).
-be kerüljön (11. segédfeladat).
Az így kapott ![]() szakasz
szakasz ![]() pontja lesz
pontja lesz ![]() tükörképe.
tükörképe.
II. eset: Ha az adott ![]() egyenes nem metszi a
egyenes nem metszi a ![]() kört.
kört.
Ekkor a kör tetszőleges ![]() pontjából párhuzamost húzunk
pontjából párhuzamost húzunk ![]() -vel. Így megkapjuk az előző I. eset
-vel. Így megkapjuk az előző I. eset ![]() egyenesét, a feladatot visszavezettük I. megoldására. (És persze akkor is végrehajthatjuk a szerkesztést, ha
egyenesét, a feladatot visszavezettük I. megoldására. (És persze akkor is végrehajthatjuk a szerkesztést, ha ![]() éppen érinti a kört.)
éppen érinti a kört.)
Zárás
Ha már eddig eljutottunk a szakkörön, akkor talán érdemes Steiner nevezetes szerkesztési tételét is megbeszélni. A „csakvonalzós” tétel szerint az euklideszi szerkesztések (két egyenes metszéspontjának, egyenes és kör metszéspontjainak, két kör metszéspontjainak szerkesztése) elvégezhetők csak vonalzó használatával is, ha adott a síkon egy kör, amelynek a középpontját ismerjük.
Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium









