Bíró Bálint: Geometriai problémák és a GeoGebra

1. Geometriai problémák és a GeoGebra

I. Bevezető gondolatok

A geometria tanításának ma az egyik alapvető problémája, hogy a matematika oktatásán belül ez a terület érzékelhetően háttérbe szorult. A gondok természetesen nem a kiváló képességű, a geometria iránt érdeklődő és szorgalmas tanulókkal kapcsolatban jelentkeznek.

A geometria háttérbe szorulását tekintve a tananyag jelentős változásai, modernizációja, illetve csökkentése nem kedvező irányban hatnak. Ugyanakkor evidenciának gondolom, hogy a geometriát magas szinten ismerő és értő hallgatókra van szüksége például az egyetemek gépész és építész karainak, de nem hagyható figyelmen kívül az a szűkebb réteg sem, akik majd az egyetemek oktatói-kutatói karát alkotják.

Ezért is szükséges foglalkozni a geometria oktatásának kérdéseivel, azzal például, hogy a mai általános- és középiskolás korosztályok számára hogyan tehetnénk érdekesebbé a geometria különféle területeit¹. Ezzel kapcsolatban nagyon jó üzenetet hordoznak a különféle országos és nemzetközi versenyeken megjelenő geometriai témájú szép feladatok.

Más korban élünk, mint akár csak húsz évvel ezelőtt, a technikai feltételek és lehetőségek ugrásszerűen megváltoztak, mégpedig pozitív irányba. Ezért a matematika, ezen belül a geometria tanításának együtt kell haladni a kor kínálta lehetőségekkel.

Az a cél, hogy szemléletessé és érdekessé tegyük a geometriai tananyagot, elérhetőnek tűnik, és szükséges is, hogy ebbe az irányba lépéseket tegyünk. Ezek a lépések önmagukban nyilvánvalóan nem elegendők, hiszen a modern szemléltető eszközök használata nem helyettesítheti a logikus gondolkodást, megfelelő életkorban a szigorú bizonyítást, a feltételek vizsgálatát, általában a geometriai ismereteket.

II. A GeoGebra szerkesztőprogram és felhasználási lehetőségei

A szemléletesség a táblai körző és vonalzó, illetve fehér és színes kréta használatán túl jelentősen növelhető azzal, ha például a GeoGebra szerkesztőprogram alapján készített rajzokat tanulmányozunk tanórán vagy szakkörön. A GeoGebra szerkesztőprogram használatának alapkérdéseivel ebben az írásban részletesen nem foglalkozom, ezekkel kapcsolatban sokféle kitűnő szakkönyv, használati útmutató ([1]), egyetemi szakdolgozat jelent meg.

A szerkesztőprogram ingyenesen letölthető a https://www.geogebra.org/download internetes oldalról, ahol mindig több program aktuálisan legfrissebb változata található. Ezek közül legjobban használhatónak a GeoGebra Classic 5 mondható. A letöltő oldalon az „Anyagok” menüpontban kész GeoGebra-munkalapok, szemléltető animációk hosszú sora található, rendkívül sok témakörben és sokféle korosztály számára (https://www.geogebra.org/materials). A GeoGebra-oldalon található anyagok egy része angol nyelvű, de vannak magyar nyelvűek is, például dr. Szilassi Lajos tanár úr és mások nagyszerű munkái. Praktikus regisztrálni a GeoGebra letöltő oldalon, mert ezzel bármely, az oldalra föltett ábra, animáció, szemléltető, és az oktatásban is kiválóan használható anyag elérhető és letölthető. Megjegyzendő, hogy ugyanez az oldal androidos okostelefonra telepíthető GeoGebra programokat is felkínál (például Graphing Calculator, Geometry, 3D Graphing), ezeket a Google Play szolgáltatással tölthetjük le okostelefonra. Nem mellesleg ugyanezen szolgáltatással olyan nagyszerű, a tanulók szemléletét formáló és logikus gondolkodását fejlesztő geometriai játékok telepíthetők telefonra, mint a Pithagorea, Pithagorea 60, és az Euclidea.

A GeoGebra szerkesztőprogram sokoldalúan használható a tanítási gyakorlatban, különféle érdeklődésű és felkészültségű, egymástól egészen eltérő képességű csoportokban is.

Az írás további részeiben először két példát mutatok be a GeoGebra használatára egy emelt szintű érettségire előkészítő csoportban (fakultációs csoport), ezután néhány további alkalmazási lehetőséget említek meg, végül egy matematika szakkörre szánt és nehezebb feladatokat tartalmazó példasort szeretnék elemezni.

III. Két példa a GeoGebra alkalmazására a tanítási gyakorlatban

A GeoGebra nem csak elemi geometriai tételek és feladatok szemléltetésére alkalmas. Sokoldalúan használható például a függvények elemi vagy magasabb szintű tárgyalásakor, illetve a koordináta-geometria tanulása-tanítása, vagy éppen az érettségire való felkészülés során.

Egy 11. évfolyamos, emelt szintű érettségire előkészítő csoportban például a körök érintőinek tárgyalását a GeoGebra segítségével végeztük. Ehhez részben a Geometriai feladatok gyűjteménye II. kötetéből választottam gyakorló feladatokat, részben pedig saját példákat készítettem, törekedve arra, hogy ennek az alkalmanként sok számolást igénylő feladattípusnak a megoldása apró könnyítéseket is tartalmazzon (például oly módon, hogy az egyik érintő egyenlete a kör középpontjának és sugarának, illetve az érintők metszéspontjának ismeretében könnyen felírható legyen, és csak a másik érintő igényeljen hosszabb számolást). Az órára készített munkalapok ilyen szempontok alapján készültek. Egy-egy feladatban lehetőség volt arra is, hogy a rajzon kezdetben csak nagyon kevés információ jelenjen meg. A teljesen kész ábra egésze vagy bármely részlete az eszközkészletben található „Jelölőnégyzet” funkció segítségével ugyanis elrejthető mindaddig, amíg a csoport tanulói a megfelelő számításokat elvégzik (1. ábrák).

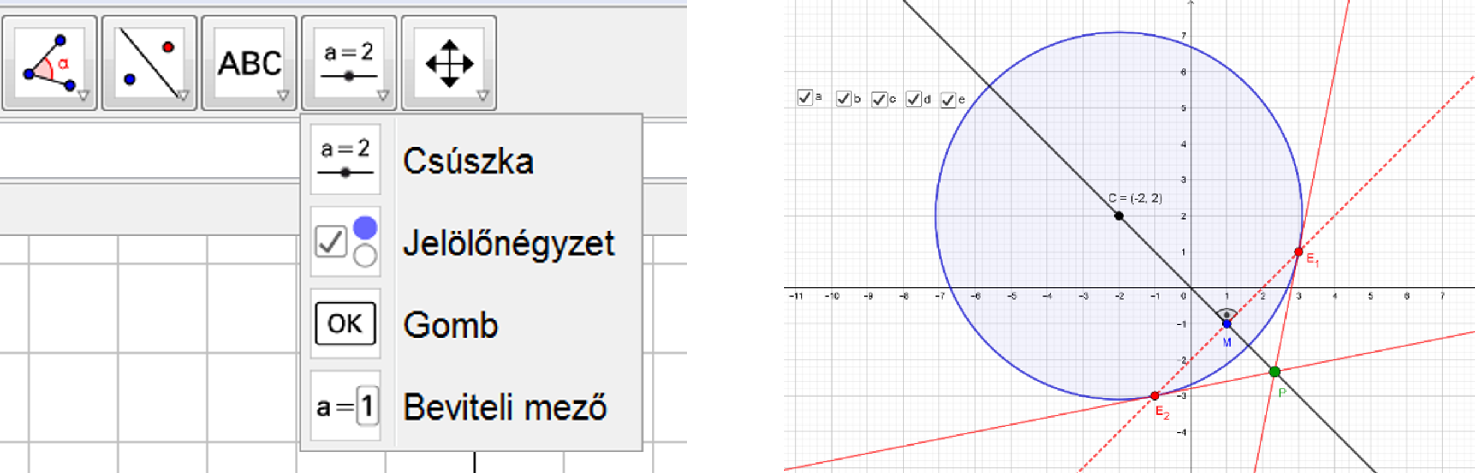
1. ábrák

Az 1. ábrák a Geometriai feladatok gyűjteménye II. kötetének 888. feladatához készültek:

Az körhöz egy kívüle fekvő pontból érintőket rajzolunk. Számítsuk ki a pont koordinátáit, ha az érintési pontokon áthaladó szelő egyenlete .

Az ábrák közül a másodikon az jelölőnégyzetek rendre a kör középpontjának, a körnek, az érintési ponton áthaladó szelőnek, az érintési pontokat összekötő szakasz felezőmerőlegesének, végül a két érintőnek az „ elrejtéséhez-megjelenítéséhez” tartoznak.

Egy másik példa ugyancsak a körök érintőivel kapcsolatos, az ehhez tartozó feladat az emelt szintű matematika érettségi vizsga 6. feladata volt a 2017/2018-as tanévben:

Adott az egyenletű kör.

a) Igazolja, hogy az pont rajta van a körön!

b) Írja fel a kör pontjában húzható érintőjének egyenletét!

c) Határozza meg az valós paraméter összes lehetséges értékét úgy, hogy az egyenletű egyenesnek és a körnek ne legyen közös pontja!

A feladat a) és b) része egyszerű algebrai, illetve koordináta-geometriai számolással megoldható. A c) rész feldolgozását a fent említett 11. évfolyamos csoportban a GeoGebra segítségével végeztük el oly módon, hogy a munkalapba egy „Csúszka” funkciót illesztettünk be. Ennek segítségével az

egyenletű kör és az origón átmenő egyenes lehetséges kölcsönös helyzeteit az paraméterre vonatkozó (az egyenes meredeksége) animációval szemléltettük (2. ábra).

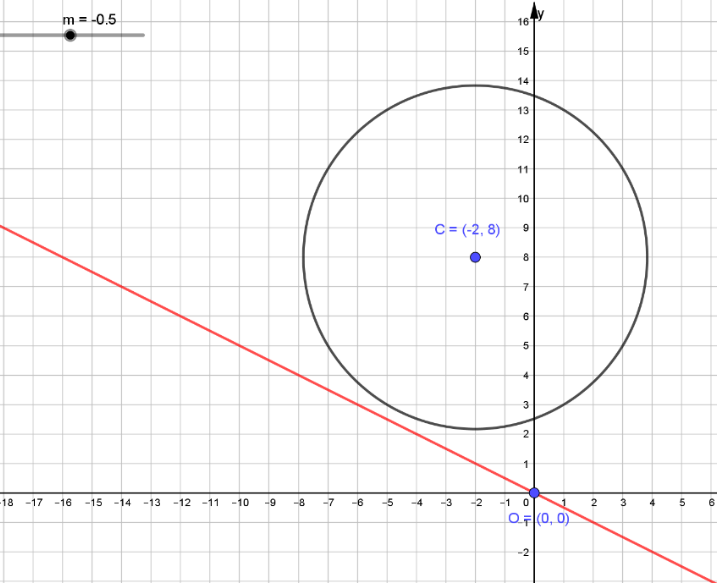
2. ábra

A szemléltetés jól sikerült, a diákok a feladatra több lehetséges megoldási módot is találtak.

A tanítási órára, versenyfeladatokkal foglalkozó szakkörre szánt rajzokat, illetve dinamikus GeoGebra-munkalapokat kezdetben célszerű, ha a tanár készíti el és mutatja be. Ugyanakkor sokféle olyan pedagógiai lehetőség van a szerkesztőprogram felhasználása során, amelyben a diákok is aktívan részt vehetnek. Jelenleg például folyik egy olyan kísérlet, amelyben a 11. évfolyamon a koordináta-geometria fejezetben a kúpszeletek bemutatását diákok csoportmunkában a GeoGebra segítségével készítik elő.

IV. A GeoGebra további felhasználási lehetőségei

A GeoGebra széleskörű lehetőségeinek köszönhetően a szerkesztőprogrammal készített munkák igen sokfélék lehetnek.

Lehetnek például teljes munkalapok, vagy munkalapok képeinek exportálásával készült és kinyomtatott rajzok. Készíthetünk Powerpoint diába illesztett képeket, vagy akár diasorozatokat is. Egy dián is megmutatható egy feladat, tétel bizonyításának összes rajzi lépése, exportált és pontosan egymásra illesztett ábrák egymásutánjával. Utóbbi olyan módszertani lehetőséget is rejt magában, hogy a diát bemutatva és a hozzá fűzött magyarázat mértékét a csoport képességeihez igazítva házi, vagy szorgalmi feladatnak is adható a teljes bizonyítás szöveges leírása.

Ha egy tételről, feladatról a bizonyítási lépések sorrendjében képeket akarunk exportálni és azt diába akarjuk illeszteni, akkor először készítsük el egy munkalapon a teljes rajzot. Ezután az „Alakzat mutatása” funkció (alakzatra kattintva jobb egér gomb) (3. ábra) kikapcsolásával tegyünk „láthatatlanná” majdnem minden rajzi részletet, ezután pedig a megoldás lépéseinek sorrendjében fokozatosan tegyük láthatóvá a bizonyítás szempontjából fontos alakzatokat.

3. ábra

Az így előálló egy-egy rajzot a megoldás aktuális fázisának megfelelően exportáljuk .png formátumban, „nem átlátszó” módon, majd mentsük el. Eközben a munkalap rajza már ne módosuljon. A képeket egy diába a megoldási lépések sorrendjében pontosan egymásra illesztve „diavetítés üzemmódban” a feladat bizonyítása szépen és látványosan, szinte animációszerűen megjelenik. Megjegyzendő, hogy ha szép és áttekinthető rajzokat szeretnénk, akkor az egyes alakzatok betűjelét a „Szöveg” funkció segítségével „LaTeX” formátumban célszerű megjeleníteni. Elfogadható minőségű jelölést maga a program is generál, de az ilyen jelölések mozgatása korlátozott a munkalapon belül. Mind az alakzatok, mind a beszúrt szöveges tartalmak, a egyenletszerkesztővel beírt képletek méretét, színét, vastagságát a program segítségével szabályozhatjuk.

Az eddig leírtak alkalmazása a diákok számára mindenképpen látványos, de előfordulhat néhány csoportnál alkalmanként passzív befogadás. Míg az aktív és érdeklődő tanulók, csoportok a rajzok, munkalapok, diák alapján kérdéseket fognak föltenni, más csoportokat az ilyen kérdések feltevésére a tanárnak célszerű ösztönöznie. Ezért javasolható, hogy a GeoGebra használatát alapszinten tanítsuk meg a diákoknak, mindenekelőtt a program letöltését és a szerkesztő funkciók alábbi gombjainak használatát (4. ábra).

4. ábra

Segítsünk nekik, hogy a program használhatóságát, érvényességi körét megértsék és aktívan alkalmazni tudják! A program használatához természetesen a diákoknak ismerni kell elemi geometriai tételeket, azok összefüggéseit, tisztában kell lenniük az euklideszi szerkesztés lépéseivel, tudniuk kell megoldani szerkesztési feladatokat körzővel és vonalzóval, illetve az érdeklődők iskolai vagy iskolán kívüli tehetséggondozó szakkörökön, pl. az Erdős Pál Matematikai Tehetséggondozó Iskola táboraiban megismerhetik a csak körzővel, vagy csak vonalzóval végzett szerkesztéseket. A tanulóknak emellett gyakorolniuk kell a szerkesztési feladatok diszkussziójának vizsgálatát, mert ezek hiányában a GeoGebra szerkesztő funkciójának nincs igazán értelme. Ismerni kell a körzővel és vonalzóval végezhető szerkesztéseket azért is, mert a versenyeken csak ilyen eszközöket használhatnak.

V. Nehéz geometriai problémák és a GeoGebra

Egy feladathoz készített GeoGebra-munkalap nem csak pontosabb, mint a körzővel, vonalzóval, ceruzával papíron vagy krétával a táblán létrehozott rajz, de nem elhanyagolható előnye, hogy a legtöbb esetben új feladatok szerkesztésére, összefüggések felismerésére is ösztönözhet diákot és tanárt egyaránt.

A továbbiakban a 2018-as győri Rátz László Vándorgyűlésen elhangzott előadáson tárgyalt geometriai feladatok közül mutatok be néhányat. A feladatok megoldásának mindenre kiterjedő részletes leírása meghaladná az írás kereteit, ezért a feladatokhoz a megoldás vagy bizonyítás néhány részletét tükröző rajzot készítek, és általában vázlatos megoldást adok. Fontosnak tartom a megoldásokhoz fűzött megjegyzéseket, azonban sem a rajzokról, vagy a megoldások vázlatairól, sem a hozzájuk fűzött megjegyzésekről nem gondolom, hogy azok az egyedül lehetséges megoldás részei lennének. Ahol az ismert, mindenütt megjelölöm a feladat forrását.

A feladatokat és a megoldásokat leginkább egy, a húrnégyszögekkel, kerületi és középponti szögek tételével és az ezekhez kapcsolódó más elemi geometriai állításokkal foglalkozó, matematikaversenyre előkészítő szakkörön célszerű felhasználni, ahol a megoldási ötleteknek, a feladatok feltételeinek, az itt le nem írt másfajta megoldásoknak, a feladatok által inspirált új ötleteknek az elemzésére is van lehetőség. Szakkörön az alábbiakban tárgyalt feladatanyag tetszőleges, és az adott szakkör igényeihez mért bővítése is ajánlott.

1. Az háromszögben és , a háromszög körülírt körének középpontja az pont. A   szögfelezője a pontban metszi az oldalt. Bizonyítsuk be, hogy a háromszög körülírt    körének középpontja az háromszög pontból induló magasságvonalára illeszkedik.

Megoldási vázlat: A megoldáshoz készített GeoGebra munkalapból két rajzot exportáltunk (5. ábrák).

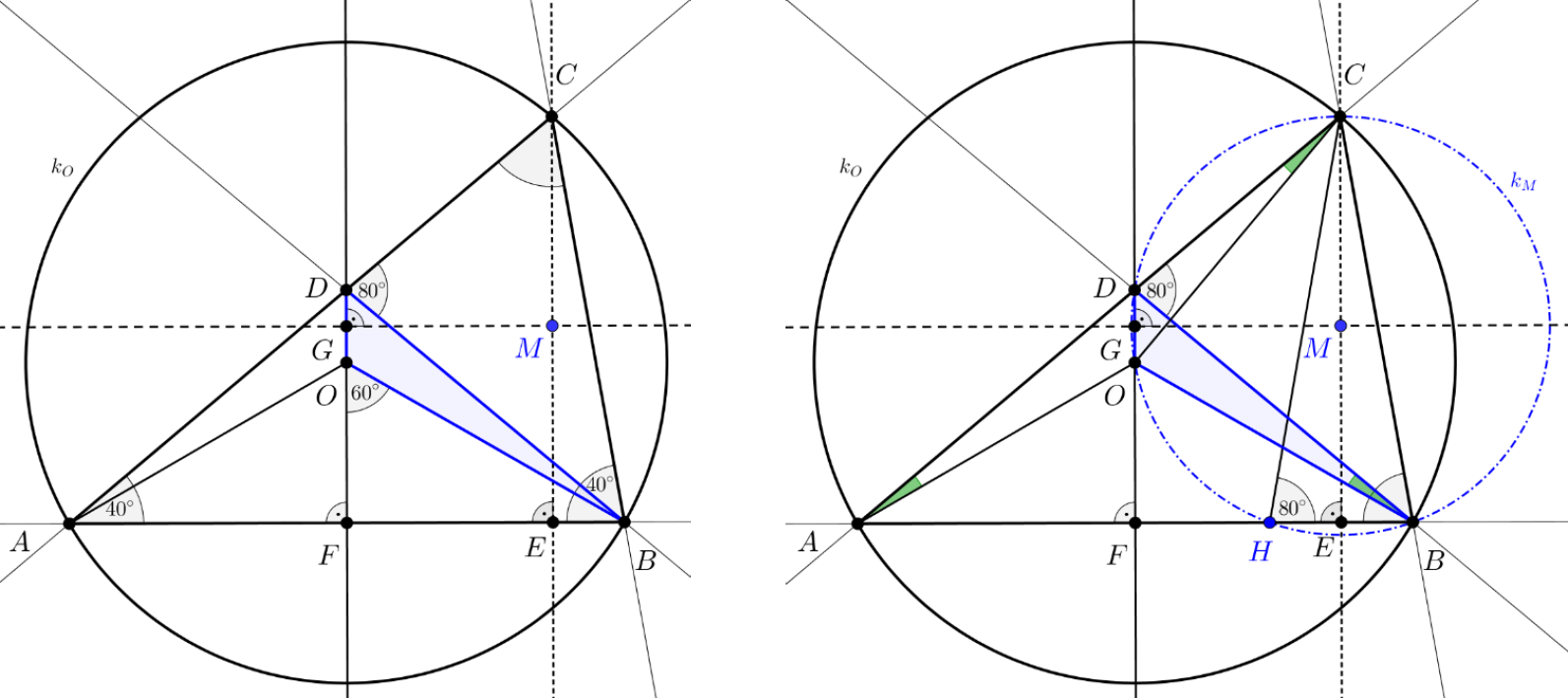
5. ábrák

Az háromszög belső szögeinek összege , ezért , vagyis az háromszög hegyesszögű, ezért az ábrákon -val jelölt körülírt körének középpontja a háromszög belső pontja, a pontból induló magasságvonal -vel jelölt talppontja pedig az szakasz belső pontja.

A egyenes felezi a -et, így , ebből következik, hogy a háromszög egyenlő szárú, tehát . Eszerint az szakasz felezőmerőlegesére illeszkedik a pont, úgy, hogy az a szakasz belső pontja, ellenkező esetben a kör középpontja az háromszög külső pontja lenne.

A szakasz felezőpontját -vel jelöltük, a háromszög körülírt körének középpontja illeszkedik a szakasz felezőmerőlegesére, ez az egyenes az háromszög pontból induló magasságvonalát az pontban metszi. A feladat megoldásához elegendő bizonyítani, hogy az pont a háromszög körülírt körének középpontja.

Először kiszámítjuk a háromszög szögeit. A középponti és kerületi szögek összefüggése szerint az egyenlőszárú háromszögben , ezért , ebből pedig adódik. A derékszögű háromszögben pedig , és így .

A háromszög két szöge tehát és , ezzel azt kapjuk, hogy  Ugyancsak a középponti és kerületi szögek összefüggése miatt az egyenlőszárú háromszögben , így .

Azt kaptuk tehát, hogy az egyenes ugyanazon oldalán fekvő és pontokból az szakasz egyaránt -os szögben látszik, hiszen , ez pedig azt jelenti, hogy a háromszög körülírt körére illeszkedik a pont.

Ezután megrajzoljuk a háromszög -mel jelölt körülírt körét, amelynek az oldallal való második metszéspontját -val jelöltük.

Az háromszög körülírt körében a középponti és kerületi szögek összefüggéséből adódik, hogy , eszerint a szakasz az pontból -os szögben látszik. A szakasz a háromszög körülírt körének húrja, ezért ez a húr a kerületi szögek tétele miatt a kör pontjából ugyancsak -os szögben látszik. Ezért a háromszög egyenlőszárú, amelynek alapját a egyenes merőlegesen felezi. Mivel pedig a háromszög körülírt körében és húrok, amelyek felezőmerőlegesei rendre a és egyenesek, ezek metszéspontja tehát a háromszög körülírt körének középpontja. Ezzel igazoltuk a feladat állítását.

Megjegyzések:

a) A feladat a verseny 10. évfolyamának 5. feladata volt és meglehetősen nehéznek bizonyult. A versenyzők általában felismerték a feladatban a kerületi szögek tételét, de azt már nem mindenki, hogy a háromszög körülírt körének középpontjához elegendő a szakasz felező merőlegesének és a magasságnak az metszéspontját vizsgálni.

b) A feladat „születése” lényegében egy olyan feladatszerkesztői szándék „majdnem véletlen” eredménye, amely adott szögekkel rendelkező háromszögek speciális tulajdonságait vizsgálta (számos ilyen feladatot ismer a szakirodalom). A feladat ötlete – a megadott szögekkel rendelkező háromszöghöz készített rajz alapján – annak felismerésén alapult, hogy a , , , pontok egy körön vannak.

2. Az húrnégyszögben megrajzoljuk az és szögfelezőit, ezek a szögfelezők az oldalt rendre az és pontokban metszik. Hasonlóképpen a és szögfelezői a oldalt rendre a és pontokban metszik. Bizonyítsuk be, hogy az , , , pontok egy körön vannak.

Megoldási vázlat: A feladat egyik lehetséges megoldása inverzió alkalmazásával történt. Az ehhez megoldáshoz készített GeoGebra munkalapból az alábbi két rajzot exportáltuk (6. ábrák).

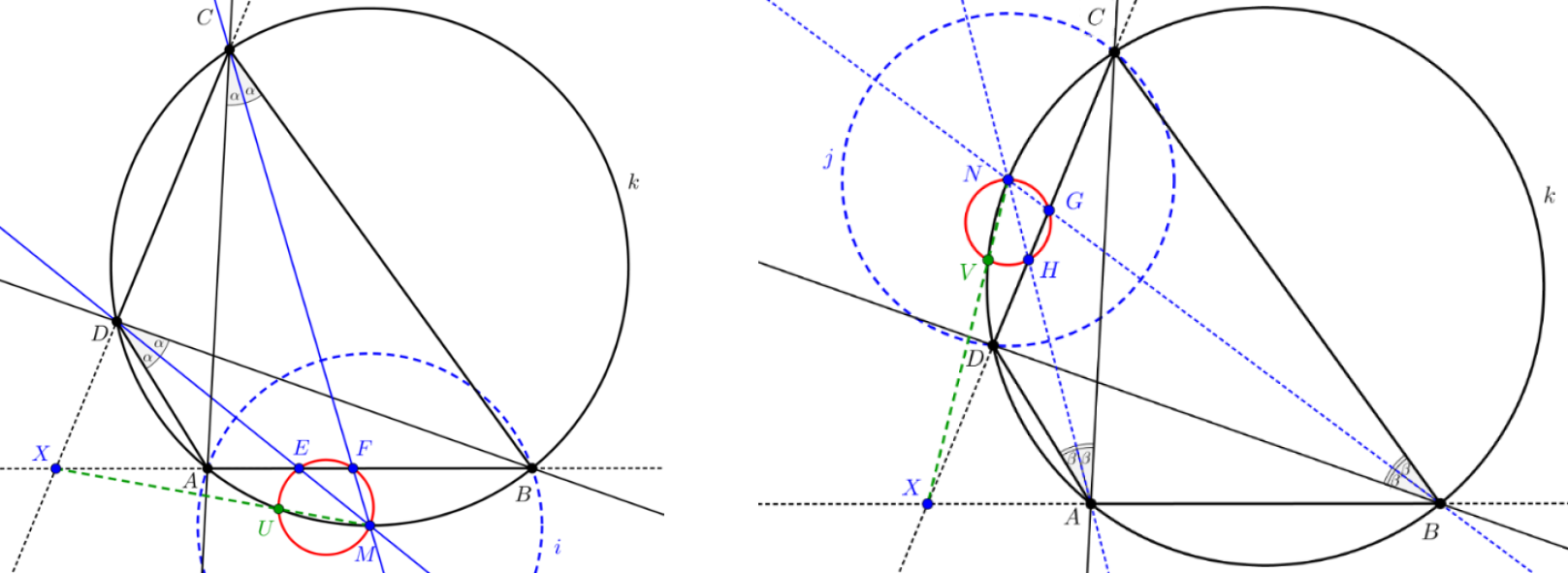
6. ábrák

A feladat megoldásához feltesszük, hogy a húrnégyszög és egyenesei nem párhuzamosak (a párhuzamos eset lényegében triviális), metszéspontjuk az pont.

A kerületi szögek tétele miatt egyenlő nagyságú és szögfelezői a húrnégyszög körülírt körének pontjában metszik egymást. Egyenlő nagyságú kerületi szögekhez egyenlő hosszúságú húrok tartoznak, ezért Hasonlóképpen adódik, hogy a és szögfelezői a körülírt kör pontjában metszik egymást és .

Tekintsük az , illetve középpontú, , , illetve , pontokon átmenő , alapkörökre vonatkozó inverziókat. Az középpontú inverzió alkalmazásakor az ponton át nem menő egyenes képe az ponton átmenő kör, a pontok képei rendre az pontok, az pont képét -val jelöltük.

Az középpontú inverzió esetén pedig az ponton át nem menő egyenes képe az ponton átmenő kör, az pontok képei rendre a pontok, az pont képe legyen .

Az és egyenesek képeként kapott körökhöz, illetve e húrnégyszög körülírt köréhez az pontból húzott szelődarabok szorzatára felírhatjuk, hogy , illetve ezekből következik az egyenlőség. A metsző húrokra vonatkozó tétel megfordítása szerint ebből az következik, hogy az pontok egy körön vannak.

Megjegyzések:

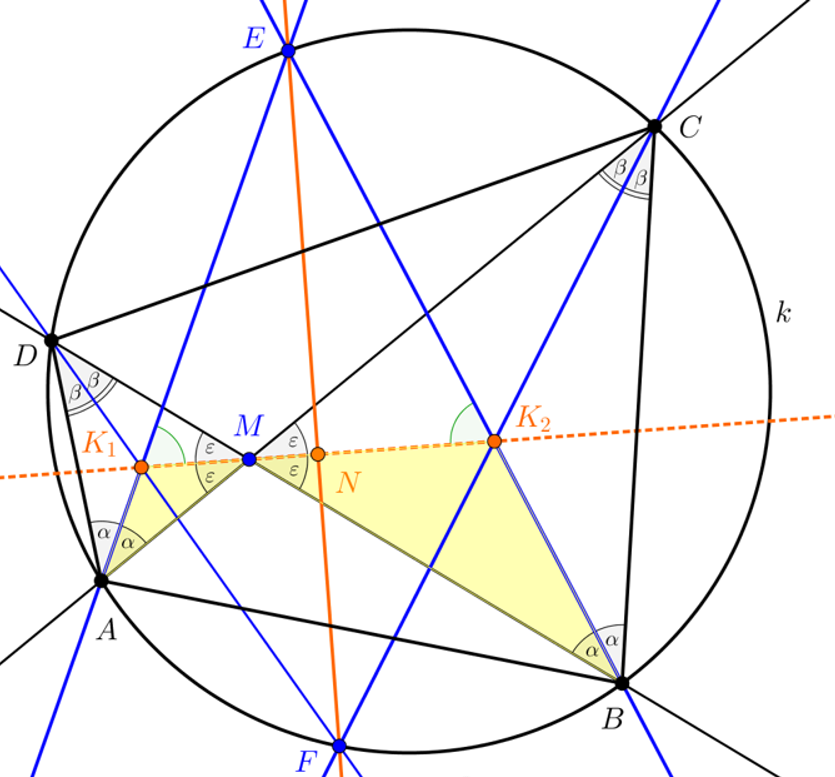
a) A feladathoz készített (esetleg diába illesztett) GeoGebra-munkalapon például az , , pontok köré írt kört megrajzolva a „Kapcsolat két alakzat között” funkció (lásd 7. ábra) segítségével ellenőrizhetjük (kifejezetten szemléltető jelleggel és nem a bizonyítás szándékával), hogy ezen a körön rajta van a pont is. Ugyanitt szemléltethetjük azt is, hogy az , , , pontok bármelyikének elmozdításával az , , , pontok mindig húrnégyszöget alkotnak. Megjegyzendő, hogy a feladat összetettsége miatt elemi geometriai ismeretek (kerületi szögek tétele, metsző húrok tétele, hasonlóság, inverzió...) nélkül a munkalap valóban csak szemléltetésre alkalmas.

7. ábra

b) A feladat hasonlóság alkalmazásával, inverzió nélkül is megoldható. A feladat eredeti ötlete abból a kézenfekvő elemi geometriai tételből (és a hozzá készült ábrából) keletkezett, hogy az és szögek szögfelezői az ív felezőpontjában metszik egymást.

3. Az húrnégyszögben az és átlók metszéspontja . Megrajzoltuk a és szögfelezőit, ezek a szögfelezők az húrnégyszög körülírt körét rendre az és pontokban metszik. Bizonyítsuk be, hogy az egyenes merőleges az felezőjére.

Megoldási vázlat: A megoldás menetének leírásához ezúttal elegendőnek látszik a GeoGebra munkalapból exportált egyetlen rajz is (8. ábra).

8. ábra

Az és szögfelezői a pontokat nem tartalmazó ív felezőpontjában, a és szögfelezői pedig az pontokat nem tartalmazó ív felezőpontjában metszik egymást. Az és , illetve és szakaszok metszéspontjait rendre -vel jelöltük. Ezek a pontok az , illetve háromszögek beírt köreinek középpontjai, ezért összekötő egyenesük felezi az és csúcsszögeket.

Az ábra jelöléseivel az háromszögben , tehát a háromszög egyenlő szárú háromszög.

Hasonlóképpen láthatjuk be, hogy háromszögben , tehát a háromszög is egyenlő szárú. Ezt azt is jelenti, hogy az négyszög deltoid, amelynek és átlói merőlegesek egymásra. Ez pedig a bizonyítandó állítással egyenértékű.

Megjegyzés:

A példa az előző feladat kiinduló ötletének (húrnégyszögben bizonyos szögek felezőinek berajzolása) nyomán született. Ez is azt mutatja, hogy ugyanabból a kiinduló ötletből, illetve az ahhoz készített rajzból akár több feladat is születhet.

4. Az hegyesszögű háromszög oldala mint átmérő fölé rajzolt kör az oldalt az pontban, az oldalt az pontban metszi. Legyen az háromszög körülírt köre . Az ponton át rajzolt tetszőleges egyenes a és köröket rendre a és pontokban metszi. Mutassuk meg, hogy a szakasz felezőpontja az háromszög Feuerbach-körére illeszkedik.

Megoldási vázlat: A GeoGebra munkalapból exportált két rajz látható a 9. ábrákon.

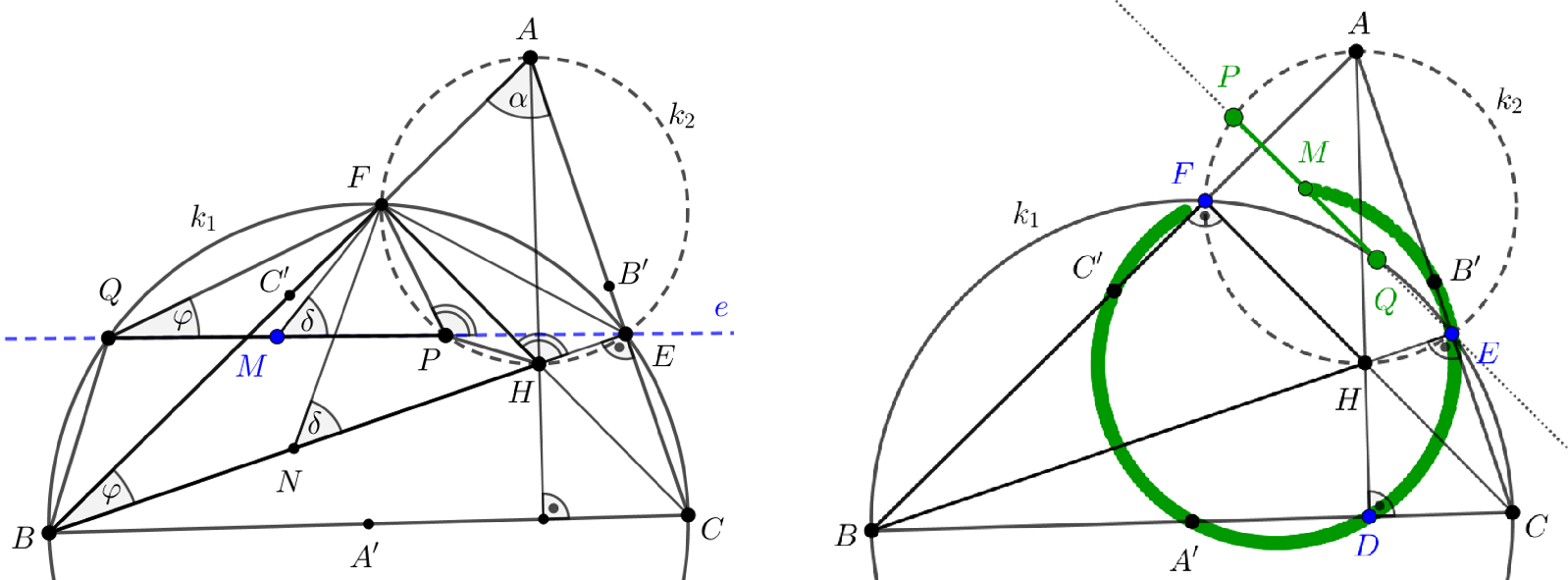
9. ábrák

A pont az háromszög magasságpontja, a magasságszakasz felezőpontja, a megfelelő háromszögoldalak felezőpontjai , , , a szakasz felezőpontja .

A kerületi szögek tétele szerint a körben , a körben pedig ezért , így .

Ez azt jelenti, hogy az és hasonló háromszögek (másképpen fogalmazva: van olyan középpontú forgatva nyújtás, amely az egyik háromszöget a másikba viszi át), amelyekben az és megfelelő oldalakhoz tartozó súlyvonalak, és így az oldalakkal azonos nagyságú szöget zárnak be, azaz , de akkor is igaz.

Az egyenes ugyanazon oldalán levő , pontokból az szakasz tehát azonos nagyságú szögben látszik, vagyis az , , , pontok egy körön vannak. Mivel mind az , , mind az pont ismert, hogy az háromszög Feuerbach-körére illeszkedik, ezért az pont is rajta van az háromszög Feuerbach-körén.

Megjegyzés:

A feladathoz az előadáson egy diát mutattam be, amelyen diavetítés üzemmódban először a teljes rajz jelent meg, kattintásra a rajz eltűnt és megjelent két GeoGebra-munkalap (ez a „megjelenés-eltűnés” a diasorozatok animációinak menüpontjában állítható be). Az első munkalap megnyitásakor a pont animálásával (jobb egér gomb) szemléltethetjük a pont lehetséges helyzeteit. Az animálás leállítása után az algebra ablak felhasználásával láthatóvá tehetjük az egyenest, a pontot, a szakaszt és az pontot (ebben a sorrendben célszerű). Ezután az pontra „aktivizáljuk” a nyomvonal funkciót (jobb egér gomb) és a pontot újra animáljuk. Ezzel szemléletesen bemutathatjuk, hogy az pont nyomvonala a pont mozgása során egy kör, amely áthalad az oldalfelező pontokon, a magasságok talppontjain, ez a kör pedig a Feuerbach kör. Ennek az animációnak egy részlete látható a 9. ábrák közül a másodikon.

5. Az hegyesszögű háromszög magasságvonalainak talppontjai a , , oldalakon rendre , , , az háromszög magasságpontja . Jelölje az mint átmérő fölé rajzolt kört , a háromszög körülírt körét . Vegyük föl a körnek a pontot nem tartalmazó ívén az , pontoktól különböző pontot. A egyenes a kört másodszor a pontban metszi és legyen a szakasz felezőpontja . Mutassuk meg, hogy az , , egyenesek egy pontban metszik egymást.

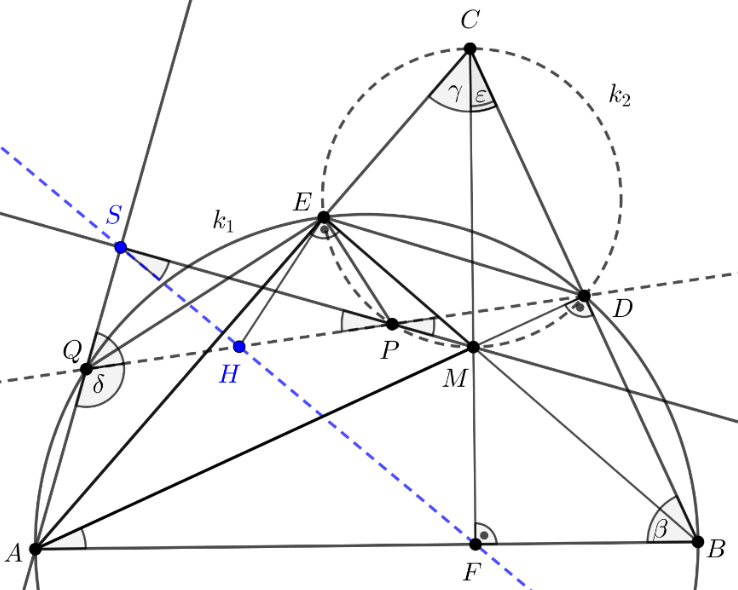
Megoldási vázlat: Jelöléseinket a 10. ábrán láthatjuk.

10. ábra

Mivel az háromszög hegyesszögű, ezért a magasságok , , talppontjai az egyes oldalak belső pontjai. A háromszög körülírt köre áthalad a ponton is, hiszen nem más, mint a szakasz, mint átmérő fölé írt Thalész-kör. Nyilvánvaló továbbá, hogy az mint átmérő fölé írt körre illeszkednek a és magasságtalppontok, tehát ezek a , körök közös pontjai.

A háromszög szögeire a szokásos jelöléseket alkalmazzuk, azaz és , ezzel a szögre teljesül, hogy .

Az ábrán az és egyenesek metszéspontját -sel jelöltük. Az egyenes a szakaszt a pontban metszi. A feltételek miatt az pont az félegyenesen, a ponton túl helyezkedik el, és emiatt a pont a szakasz belső pontja. Elegendő bizonyítani, hogy a pont és a szakasz felezőpontja azonos.

A körben , ezért a kerületi szögek tétele szerint , a csúcsszögek egyenlősége miatt viszont

(1)

A körre illeszkednek az pontok, ezért húrnégyszög, tehát az ábra szögére teljesül, hogy , ebből pedig azonnal adódik, hogy

(2)

Az (1) és (2) összefüggésekből kapjuk, hogy a háromszög derékszögű, éspedig tehát az és egyenesek az pontban merőlegesen metszik egymást. Így az négyszög húrnégyszög, mert két szemközti szögének összegére

Az húrnégyszög körülírt körében és azonos ívhez tartozó kerületi szögek, ezért ugyanakkor, mivel , ezért

(3)

(1) szerint , ez pedig (3)-mal összevetve azt jelenti, hogy a háromszög egyenlő szárú, amelyben a megfelelő szögek egyenlősége miatt

(4)

A (2)-ből az következik, hogy . A és a (3)-ból adódó együttesen azt jelentik, hogy is fennáll. Ez ekvivalens azzal, hogy a háromszög is egyenlő szárú, vagyis

(5)

A (4) és (5) eredményeink szerint , vagyis a pont valóban felezi a szakaszt, tehát a pont a feladat szövegében szereplő felezőponttal valóban azonos.

Megjegyzések:

a) A pont a derékszögű háromszög körülírt körének középpontja.

b) Az előző feladat szerint a pont az háromszög Feuerbach-körére illeszkedik.

c) A feladat ötlete az előző feladathoz készített munkalap rajza alapján született.

6. Legyenek az hegyesszögű, nem egyenlő szárú háromszög és oldalainak felezőpontjai rendre és , a háromszög körülírt körének középpontja , magasságpontja . Az háromszög körülírt köréhez az pontban húzott érintő és metszéspontja , a körülírt körhöz a pontban húzott érintő és metszéspontja . Mutassuk meg, hogy a egyenes merőleges az egyenesre.

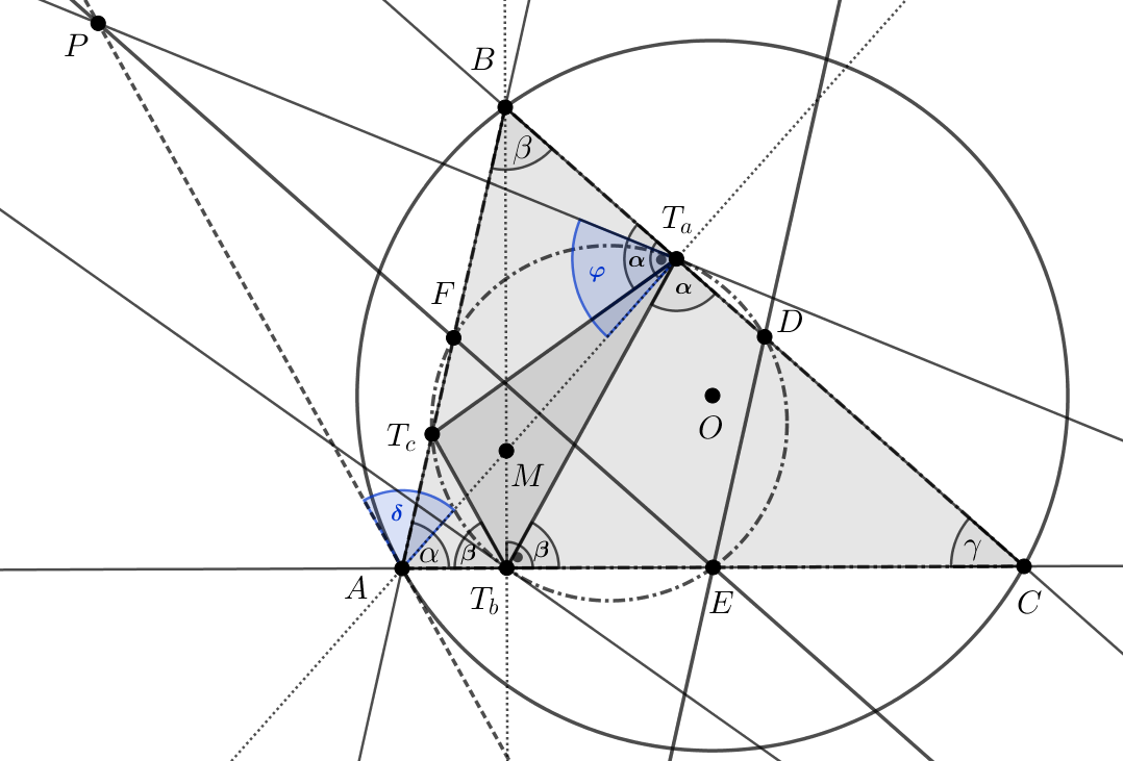
Megoldási vázlat: A megoldáshoz egy GeoGebra munkalap egy rajzát exportáltuk (11. ábra).

11. ábra

Elemi geometriai eszközök felhasználásával (kerületi szögek tétele, a magasságok talppontjai által alkotott háromszög egy oldala akkora szöget zár be a háromszög egy oldalával, mint a háromszög egyik szöge, a háromszög magasságvonalai a talpponti háromszög szögfelezői) egyszerűen bizonyíthatjuk azt a segédtételt, amely szerint a háromszög egy csúcsában a körülírt körhöz és a csúcsból induló magasság talppontjában a háromszög Feuerbach-köréhez húzott érintők a magassággal azonos nagyságú szöget zárnak be.

Ezért, ha a két érintő metszéspontját -vel jelöljük, (amely pont mindkét körre nézve külső pont) akkor a 11. ábra megjelölt szögeire , vagyis .

A segédtételből az is adódik, hogy , vagyis a pont rajta van az szakasz felezőmerőlegesén.

Megmutatjuk, hogy a , pontoknak az háromszög körülírt körére és Feuerbach-körére vonatkozó hatványa egyenlő. Nyilván elegendő ezt a feladatban szereplő egyik, például a pontra bizonyítani.

Mivel az háromszög nem egyenlő szárú, ezért az egyes csúcsokban a körülírt körhöz húzott érintők metszik a megfelelő középvonalak egyenesét. Az középvonal minden, az csúcsot a egyenes valamely pontjával összekötő szakaszt felez, tehát felezi a háromszög magasságát is, utóbbit merőlegesen, hiszen .

Az előzőek szerint , mert rajta van az szakasz felezőmerőlegesén.

A pontnak az háromszög körülírt körére vonatkozó hatványa a érintőszakasz négyzetével egyenlő, azaz .

A pontnak a Feuerbach-körre vonatkozó hatványa pedig , ebből a egyenlőség alapján következik, tehát a pontnak az háromszög körülírt körére és Feuerbach-körére vonatkozó hatványa egyenlő.

Az háromszög körülírt köre és Feuerbach-köre nem koncentrikusak, mert az nem egyenlő szárú, tehát a két körnek van hatványvonala és ez a hatványvonal egyenes.

A pont tehát illeszkedik a két kör hatványvonalára, és hasonlóan bizonyíthatjuk, hogy a pont is illeszkedik erre a hatványvonalra.

Ismeretes, hogy két kör hatványvonala a centrálisukra merőleges. A körülírt kör középpontja , magasságpontja , a Feuerbach-kör középpontja pedig az szakasz felezőpontja, így a körök centrálisa az háromszög Euler-egyenese, vagyis az egyenes. Ezzel a feladat állítását bizonyítottuk.

Megjegyzések:

a) A feladat egy, a Feuerbach-körrel kapcsolatos GeoGebra-munkalap készítése nyomán keletkezett. Pontosabban: a munkalapból exportált rajz segítségével sikerült a megoldás elején említett, és segédtételként felhasznált geometriai tulajdonságot észrevenni és azt bizonyítani.

b) A feladat következménye, hogy a pontban húzott érintő és a egyenes metszéspontjának (valamint a , pontoknak) a körülírt körre és a Feuerbach-körre vonatkozó hatványai egyenlők, azaz , ezért a , , pontok egy, az egyenesre merőleges egyenesre illeszkednek.

c) Bizonyítható, hogy a feladat megoldása során használt segédtétel minden háromszögre fennáll, így a feladat állítása minden háromszögre teljesül.

7. A hegyesszögű háromszög és csúcsából induló magasságvonal talppontja az , illetve oldalon rendre és , a oldal felezőpontja . Az és szakaszok metszéspontja , az pontnak a szakaszra eső merőleges vetülete . Bizonyítsuk be, hogy az szakasz felezi a szakaszt.

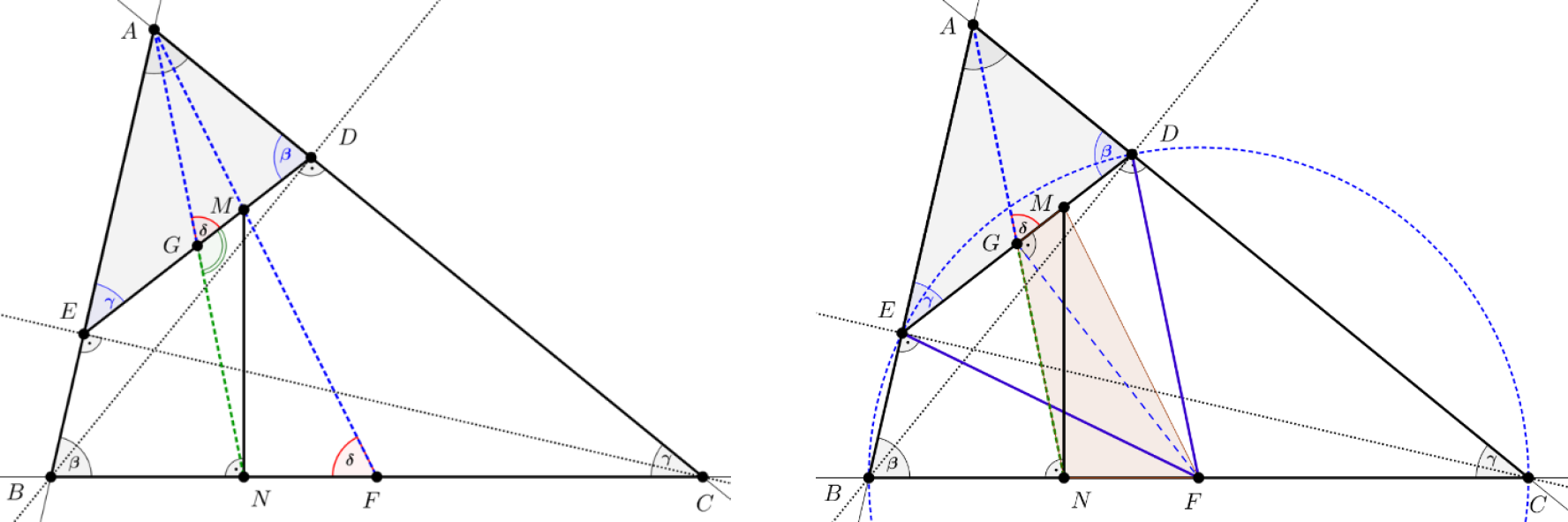
12. ábrák

Megoldási vázlat: Tekintsük a 12. ábrákat, amelyeken a szakasz felezőpontját -vel jelöltük, ezt a pontot összekötöttük az és pontokkal. Bizonyítani fogjuk, hogy .

A jelölésekben utaltunk arra a (6. feladatban is felhasznált) geometriai tételre, amely szerint az hegyesszögű háromszög talpponti háromszögének oldala az , oldalakkal rendre , szögeket zár be, ezért az , illetve háromszögek hasonlók.

Hasonló háromszögekben a megfelelő oldalakhoz tartozó súlyvonalak az oldalakkal azonos nagyságú szögeket zárnak be (ezt a 4. feladatban is alkalmaztuk), ebből azt kapjuk, hogy . Tudjuk, hogy a , pontok rajta vannak az középpontú Thalész-körön, ennek a körnek tehát egy húrja a szakasz, így pedig az merőlegesen felezi -t.

Eszerint a 12. ábrák közül a másodikon szereplő négyszög húrnégyszög, amelynek csúcsai az fölé írt Thalész-körre illeszkednek. Mivel , ezért . Ez ekvivalens azzal, hogy .

Megjegyzések:

a) A 12. ábrákon a feladat megoldásához készített GeoGebra-munkalap egy-egy rajzát látjuk. A IV. pontban leírtak szerint a bizonyítás egyes lépéseiről bemutató diát is készíthetünk, amelyen vetítési üzemmódban a bizonyítás lépései jól nyomon követhetők.

b) A 12. ábrák azt mutatják, hogy az háromszög nem egyenlő szárú, de könnyen beláthatjuk, hogy a feladat állítása egyenlő szárú háromszögre is teljesül.

c) A feladat a KöMaL B. 4749. jelű feladata volt, a KöMaL-ban a fentitől eltérő bizonyítás jelent meg.

d) A feladat rokonságot mutat egy vietnami versenyfeladattal, amelyben az pontnak az és oldalakra eső merőleges vetületét rendre , -val jelölve bizonyíthatjuk, hogy felezi a szakaszt. Bizonyítható az is, hogy az háromszög magasságpontja , valamint az, hogy a négyszög parallelogramma.

8. Az hegyesszögű háromszög körülírt körének középpontja , magasságpontja . Tükrözzük az pontot a oldal felezőmerőlegesére, a pontot a oldal felezőmerőlegesére, végül a pontot az oldal felezőmerőlegesére, a tükörképpontok rendre , , . Mutassuk meg, hogy az háromszögnek az ponthoz tartozó Simson-Wallace-egyenese merőleges a egyenesre.

Megoldási vázlat: Tekintsük a 13. ábrákat.

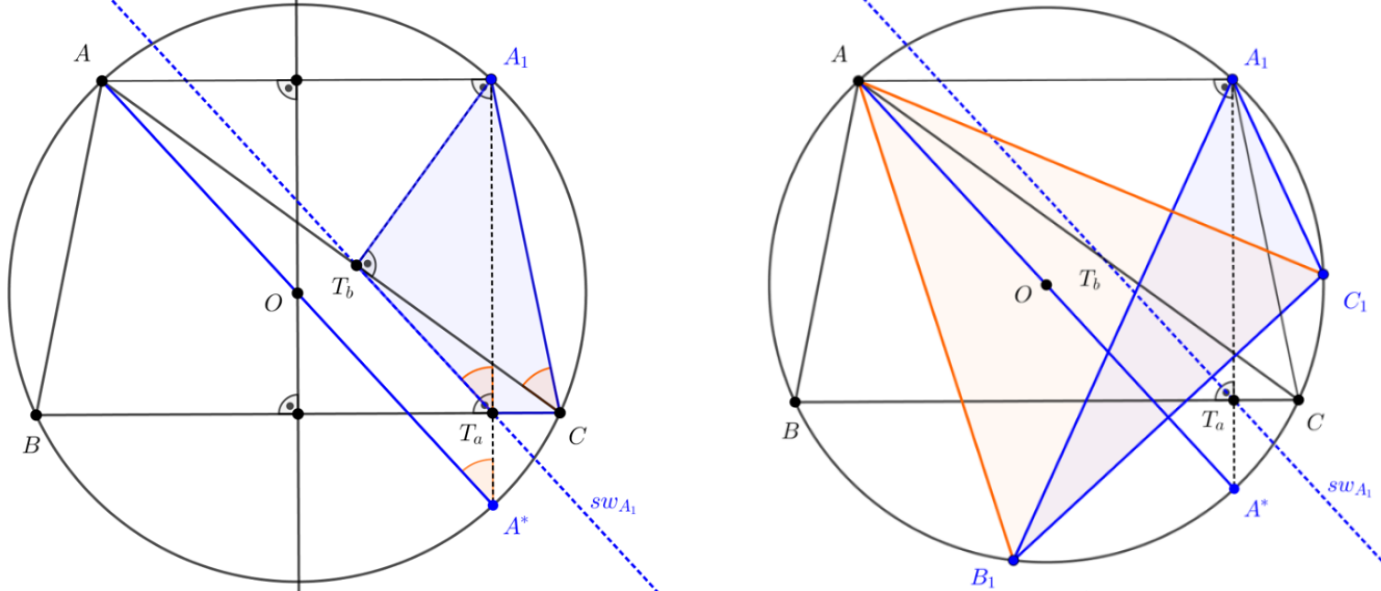
13. ábrák

A 13. ábrák közül az elsőn merőlegest bocsátottunk az pontból a és oldalakra, a talppontok rendre , , az egyenes a körülírt kört másodszor az pontban metszi.

Könnyen látható, hogy húrnégyszög, ezért a húrnégyszög köré írt körben a kerületi szögek tétele miatt . Ugyanakkor és az háromszög köré írt körben és azonos ívhez tartozó kerületi szögek, ezért egyenlő nagyságúak. Eszerint az háromszögnek az ponthoz tartozó Simson–Wallace-egyenes párhuzamos az egyenessel (ez a Simson–Wallace-egyenes általános tulajdonsága). Mivel , ezért , így az egyenes áthalad a körülírt kör középpontján. A és pontok szerkesztése miatt és egyaránt igaz, tehát az háromszög egyenlő szárú. Ezért , ez viszont azt jelenti, hogy az egyenessel párhuzamos Simson–Wallace-egyenes is merőleges a egyenesre.

Megjegyzések:

a) A feladat az egyik szép példája annak, hogy egy feladatból, illetve a hozzá készült GeoGebra-munkalap rajzaiból hányféle új feladat, tétel keletkezhet. Bizonyítható ugyanis, hogy az háromszögnek az , , pontokhoz tartozó Simson–Wallace-egyenesei egy pontban metszik egymást, valamint, hogy az háromszögnek az , , pontokhoz tartozó Simson–Wallace-egyenesei ugyancsak egy pontban metszik egymást, ráadásul ez a két pont azonos és nem más, mint annak a háromszögnek a magasságpontja, amelyet úgy kapunk, hogy az háromszöget az háromszög magasságpontjából arányban kicsinyítjük. Minden felsorolt állításnak a bizonyítása megtalálható a Matematika Tanítása 2012. /1. számában. (https://www.mozaik.info.hu/Homepage/Mozaportal/MPfolyoirat.php?op=matematika)

VI. Összegzés

Az írás nem titkolt célja volt az, hogy néhány példával rámutasson: van olyan modern eszköz (nyilván több is), amivel látványosabbá, a mai diákok számára érdekesebbé tehetik tanáraik a geometriát. Nyilvánvaló persze, hogy a GeoGebra szerkesztőprogram nem oldhat meg mindent, és nem helyettesíthetők vele az alapvető geometriai ismeretek, és az azokhoz kapcsolódó bizonyítások. Ugyanakkor az írás próbált utalni a sokoldalú alkalmazhatóságára, többféle funkciójára.

Mindenképpen szerettem volna hangsúlyozni, hogy egy-egy feladathoz készült GeoGebra-munkalap, rajz, a legtöbb esetben nem csak egy-egy feladat megoldására alkalmas, majdnem mindig új feladatok, tételek kitalálására ösztönözheti az érdeklődőt, és ilyen módon példátlan lehetőségeket rejt magában a kreativitás fejlesztéséhez. Ezért tárgyaltam részletesen 8 geometriai feladatot, amelyek közül több összefügg egymással, néhol egyik feladatból keletkezett a másik.

Nyilván még több, akár a fentieknél nehezebb feladat is bekerülhetett volna a 8 feladat közé, akár ezek helyett is. Remélem, hogy a leírtak legalább részben igazolják, hogy a GeoGebra szerkesztőprogram ilyen esetben is tud segítséget nyújtani. Márpedig, ha ez így van, akkor az írás elérte az egyik célját.

Irodalomjegyzék

[1] Markus Hohenwarter–Judith Hohenwarter: GeoGebra kézikönyv 3.2 (a kézirat utolsó módosítása 2011. 07. 1.)

 

[2] Középiskolai Matematikai és Fizikai Lapok (KöMaL)

 

[3] Vásárhelyi Éva: Térbeli feladatok megoldása GeoGebrával, Érintő Elektronikus Matematikai Lapok, 2018. június http://ematlap.hu/index.php/tanora-szakkor-2018-06/695-terbeli-feladatok-megoldasa-GeoGebraval

 

[4] Geometriai feladatok gyűjteménye I.–II., Nemzeti Tankönyvkiadó

Bíró Bálint
Egri Szilágyi Erzsébet Gimnázium és Kollégium

Lábjegyzet

¹ Ez az írás a 2018-ban a győri Rátz László Vándorgyűlésen elhangzott előadás alapján készült. Az előadásban elhangzottak azon vélemény mellett foglaltak állást, hogy a geometriát érdekessé és szemléletessé lehet és kell tenni, ehhez pedig minden olyan eszközt helyes és célszerű felhasználni, amellyel ez a cél elérhető.