A „baloldali angolok” klubjai és más extremális halmazrendszerek

Ennek a rövid írásnak az a célja, hogy bemutassa, mit takar a tudományosan és bonyolultan hangzó extremális halmazrendszerek szóösszetétel. Matematikai tételeket többféleképpen lehet csoportosítani. Az egyik lehetséges felosztás történhet az alterületek szerint. Ehhez elég megnézni egy egyetem matematikai intézetében a különböző tanszékek neveit: algebra, analízis, geometria, stb. Egy másik felosztás aszerint történhet, hogy milyen típusú kérdésre ad választ az adott tétel. Egy állítás szólhat egy általános összefüggésről, ahogy például a középiskolából jól ismert Pithagorasz tétele kimondja, hogy minden derékszögű háromszögben a befogók hosszainak négyzetösszege megegyezik az átfogó hosszának négyzetével. Egy másik állítás kimondhatja, hogy bizonyos matematikai struktúrából mennyi létezik. Kombinatorikából (ahova a mindjárt bemutatandó extremális halmazrendszerek témaköre is tartozik) középiskolában például megtanuljuk, hányféleképpen lehet a lottószelvényt kitölteni (azaz hányféleképpen lehet kiválasztani 90 számból 5-öt). És sok egyéb érdekes matematikai kérdés mellett léteznek olyanok, melyek bizonyos matematikai struktúrák közül a legnagyobbra, legkisebbre vagy valamilyen más módon legoptimálisabbra, legextremálisabbra kérdeznek rá. Megérkeztünk. (De az egyszerűség kedvéért most maradjunk a legtöbbnél.)

A bugyuta verzió (olyan mindig kell, hogy legyen mit megmosolyogni)

Képzeljük el (miért is ne, matematikáról beszélünk, képzelődjünk), hogy egy nagy angol gyár szakszervezetének 2000 tagja van. Mivel angolok (és mivel mi képzelődünk, és ilyen képzeteink vannak az angolokról régről, bár nem feltétlen a szakszervezeteikről), ezért klubokat szeretnének létrehozni. Minél többet, annál jobb. (Ez igaz az egyes emberekre is: nem sportklubokról beszélünk, ahol illik mindenkinek egyet választania és ahhoz hűségesnek lenni, hanem inkább szakkörökről: filmklub, olvasóklub, táncklub, stb. Menjen mindenki minél több klubba.) De szakszervezetekről lévén szó, erősen elitellenes érzelmeik is vannak, melyet abban próbálnak kifejezésre juttatni a klubok létrehozásakor, hogy nincs „előszobáztatás”, nem lehetnek belső körök, nincs olyan, hogy egy klub tagjainak egy része létrehoz egy szűkebb klubot. (Talán más alkalmakkor több lehetőség van megmutatni az elitellenességet, a klubalkotásnál elég lesz ennyi.) Az világos, hogy ha minden klubnak ugyanannyi tagja van, akkor a klubok megfelelnek a kívánt baloldali hevületnek, hiszen egy belső kör lényege, hogy kevesebb tagból álljon, mint a nagy klub. Aki középiskolában figyelt a lottószelvények leszámlálásánál, az tudja, hogy ilyen egyszerű módon akkor kapja a szakszervezet a legtöbb klubot, ha az összes 1000 fős csapatát a tagoknak kinevezi klubnak (és ha nem 2000-en vannak, akkor is mindig a taglétszám felét kell venni). Emmanuel Sperner 1928-ban bizonyította az extremális halmazrendszerek egyik alaptételét, miszerint az angol szakszervezet semmilyen más trükkös módon sem tud több klubot alkotni fenti ideológiájuk mentén. Nézzünk néhány más (bugyuta) példát:

az ismerkedők klubjai: az a szabály, hogy ha összeeresztik bármely két klub tagjait, akkor ne legyen mindenki idegen egymásnak, legyen valaki, aki mindkét klub tagja, és így ismer mindenkit, bárkit be tud mutatni bárkinek. (Egy kicsit okosabb gimnazista, aki át tudja fordítani ezt a szabályt matematikai nyelvezetre, vélhetően meg is tudja mondani, mi a lehető legtöbb klub, ami létrehozható.)
a rendhez mániásan ragaszkodó ismerkedők klubjai: itt annyival bonyolultabb a helyzet, mint az előbb, hogy valamiért muszáj minden klubnak 18 főből állnia. Vagy 103-ból, vagy 325-ből, a lényeg, hogy a klubokba felvehetők számának felénél kisebb számot mondjunk. (Az okos gimnazista kitalálhatja, hogy ez miért szükséges.) Az ilyen szabályok mellett lehetséges legtöbb klub számát Erdős, Ko és Rado határozták meg, s ez az extremális halmazrendszerek másik alaptétele.
a félénk tinderezők klubjai: a félénk tinderezők annak örülnek (örülnének), ha lenne valaki, aki bemutatná őket az új klubban, azaz megtartják az ismerkedők klublétrehozási szabályát. Viszont minél több emberrel szeretnének megismerkedni minél hamarabb (de azért sok-sok klubot szeretnének ők is), azaz nem szeretnék idejüket már ismert emberek nézegetésére vesztegetni. Tehát másik szabályuk, hogy bármely két ember legfeljebb egy közös klubban lehet benne. A választ (mármint, hogy mennyi a lehető legtöbb így létrehozható klub) deBruijn és Erdős egy 1948-as tétele adja meg.

A hivatalos verzió (definíciók, formulák, meg minden)

Nézzük, hogy a kissé erőltetett szabályú klubok hogyan határozhatók meg matematikai fogalmakkal. A klubokba nem akárki léphet be, csak a szakszervezet tagjai, a társkeresők, a tinderezők, azaz van egy $X$ alaphalmaz, ahonnan a tagok, azaz $X$ elemei kikerülnek. Egy klub az összes lehetséges tag egy része, azaz az $X$ alaphalmaz egy $F$ részhalmaza, amit $F\subseteq X$ módon jelölünk. Ilyen $F_1,F_2,\dots$ halmazokat gyűjtünk egy $\mathcal{F}$ halmazrendszerbe. Azt hogy minden $\mathcal{F}$ -beli halmaz $X$ részhalmaza, így szokás jelölni: $\mathcal{F} \subseteq 2^X$ . Lássuk, hogy a klublétrehozási szabályok hogyan definiálhatóak.

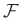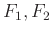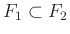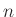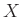A baloldali angolok szabálya szerint egyik klub sem előszobája a másiknak, azaz egyik, a kluboknak megfelelő halmaz sem lehet szigorúan kisebb része a másiknak. Tehát nincs két $\mathcal{F}$ -beli $F_1,F_2$ halmaz, amire $F_1 \subset F_2$ teljesülne. 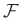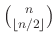Az ilyen rendszereket antiláncnak nevezik (tényleg, nemcsak a baloldaliak kedvéért) és Sperner tétele szerint egy $n$ elemű $X$ alaphalmazon vett $\mathcal{F}$ antilánc nem tartalmazhat több halmazt, mint ${n \choose \lfloor n/2\rfloor}$ .
Az ismerkedők szabálya, hogy bármely két klub esetében legyen valaki, aki itt is, ott is tag, azt jelenti, hogy bármely két klubot reprezentáló halmaznak van közös eleme, azaz a közös részük, a metszetük nem üres: 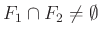$F_1\cap F_2 \neq \emptyset$ . Ezért is hívják az ilyen halmazrendszereket metszőknek és az okos gimnazisták által is belátható állítás szerint, ha az alaphalmaz 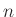$n$ elemből áll, akkor legfeljebb 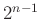$2^{n-1}$ halmazt (azaz az összes részhalmaz felét) tudunk kiválasztani ezzel a tulajdonsággal. Ha „a rendhez mániákusan ragszkodunk”, azaz minden klubnak ugyanakkorának kell lennie, az nem a tulajdonságon változtat, hanem azon, hogy melyik halmazok közül válogathatunk. Az ugyanakkora méretű halmazokból álló rendszereket uniformnak szokás nevezni. Ha a 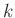$k$ méretűekre vagyunk szorítva, akkor azt úgy jelöljük, hogy 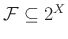$\mathcal{F} \subseteq 2^X$ helyett 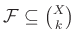$\mathcal{F} \subseteq {X \choose k}$ -t írunk. Ha 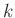$k$ nagyobb, mint az alaphalmaz fele, akkor nincs hely nem metszeni egymást (például két négyelemű, közös elemet nem tartalmazó halmazba összesen 8 elem tartozik, tehát 6 vagy 7 méretű alaphalmazon nem lehet ilyen pár). Ha viszont 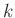$k$ legfeljebb 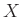$X$ méretének a fele, akkor Erdős, Ko és Rado tétele szerint legfeljebb 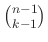${n-1\choose k-1}$ halmazt tudunk összegyűjteni egy metsző halmazrendszerbe ( 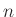$n$ megint 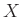$X$ méretét jelöli).
Végül a félénk tinderezők. Ők is megtartják a halmazokra vonatkozó „ne legyen üres a metszet” szabályt. Másik szabályuk szerint ugyanaz a két elem legfeljebb egy halmazhoz tartozhat. Azaz két rendszerbeli halmaz méretének kisebbnek kell lennie kettőnél. De ha a metszet nem üres, viszont kevesebb, mint két elem tartozik ide, akkor az azt jelenti, hogy a metszet mérete pontosan 1 (tehát minden 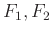$F_1,F_2$ esetén 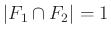$\vert F_1\cap F_2\vert=1$ ), ezért is hívhatjuk az ilyen rendszereket pontosan 1-metszőknek (bár az úgynevezett block design-ok elméletében más elnevezés használatos). DeBruijn és Erdős tétele szerint ezzel a tulajdonsággal rendelkező halmazrendszer legfeljebb annyi halmazból állhat, ahány eleme az alaphalmaz 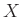$X$ -nek van.

De miért jó ez és kinek?

Az utóbbi kérdésre egy lehetséges őszinte válasz az, hogy az ilyen típusú kombinatorikai problémákon gondolkodni szerető, nem túl népes, de magyarokban némileg felülreprezentált kutatói közösségnek mindenképpen. Vannak azonban olyan halmazrendszer-tulajdonságok, amelyek megvizsgálása közvetlen alkalmazással bír. Lássunk erre két példát:

Hibajavító kódok. Tegyük fel, hogy egy kódolt üzenetet szeretnénk elküldeni. Hogy a messzi címzett biztosan el tudja olvasni az üzenetet, csak két jól megkülönböztethető karaktert (mondjuk a 0-t és az 1-et) használnánk. Első, bevezető kérdésünk, hogy milyen hosszú 0-1 sorozatokkal (kódokkal) tudjuk helyettesíteni a magyar ábécé 44 betűjét? Minden egyes karakter 2 választási lehetőség, így k hosszú 0-1 sorozatból $2^k$ darab van. Azaz a legkisebb olyan számot keressük, amire $2^k\ge 44$ . Erre vezettük be középiskolában a logaritmus függvényt: $\log_2 44$ felfele kerekítve lesz a legkisebb megoldásunk. Az igazi probléma azonban most jön: sajnos a kód néhány karaktere a nagy távolság miatt nem jut el a címzetthez, némelyik másik pedig rosszul jut el (0-ról 1-re vagy 1-ről 0-ra változik). Szerencsére azt tudjuk, hogy egy-egy kis részben, ami egy betűt kódol el, legfeljebb 3 helyen történik változás. Hogyan kódoljunk úgy, hogy az okos címzett meg tudja találni és ki tudja javítani a hibákat? Ha úgy gyűjtünk 0-1 sorozatokat, hogy bármely kettő legalább 7 karakterben eltér egymástól, akkor rendben leszünk. Ha ugyanis egy eredeti $K$ kódszó meg is változik, a torzított verzió, $T$ legfeljebb 3 változtatásnyira lesz tőle. Viszont minden $K$ -tól különböző $K’$ kódszótól legalább 4 változtatásnyira lesz $T$ , hiszen ha $K$ és $K’$ között a lehető legkevesebb, 7 különbség is volt, és ha a 3 változtatás pont ezeken a helyeken történik, akkor is marad még 4 eltérés. Azaz az üzenet megfejtőjének csak meg kell néznie, melyik eredeti kódszóhoz van az érkezett verzió a legközelebb. Azaz az lett a feladatunk, hogy megtaláljuk a legkisebb olyan $k$ számot, hogy van 44 darab $k$ hosszú 0-1 sorozat, amelyből bármely 2 legalább 7 helyen különbözik egymástól. (A 3 és 7 persze lecserélhető tetszőleges $e$ és $2e+1$ számokra. Az $e$ az angol error szóra utal.) Nagyszerű, de hol vannak itt a halmazok? Ott, hogy a $k$ hosszú 0-1 sorozatok egyszerűen megfeleltethetőek egy $k$ méretű alaphalmaz részhalmazainak. Ha a sorozat ötödik eleme 0, az azt jelenti, hogy a sorozathoz tartozó részhalmaz nem tartalmazza az alaphalmaz ötödik elemét, ha viszont 1, akkor igen. Azaz például az 1011 kód tartozik az $\{1,3,4\}$ halmazhoz, a 0011 kód a $\{3,4\}$ halmazhoz, és így tovább. Nekünk pedig halmazokra fordítva az a feladatunk, hogy meghatározzuk, hogy egy $n$ elemű alaphalmaznak legfeljebb hány olyan részhalmaza választható ki úgy, hogy bármely kettőre létezik legalább $2e+1$ elem, ami pontosan az egyikben van benne. Nem tűnik túl természetes feladatnak, de ilyen kódolást tényleg alkalmaztak különböző űrkutatási projektekben.

Kombinatorikus keresés. Ezen kutatási terület egyik legelső alkalmazása a második világháborúban született, amikor katonák vérteszteit használva kellett közülük a betegeket megtalálni. Tegyük fel, hogy hadseregünkben csak egyetlen beteg van, akit szeretnénk kiszűrni, minél kevesebb vértesztet használva. Persze csináltathatjuk a tesztet katonánként, de sokkal ügyesebben is: összeöntjük a katonák felének vérmintáját, és erre elvégezzük a tesztet. Ha a teszt nem találja a betegség jelét, máris tudjuk, hogy a hadsereg másik felében van a beteg, ha pedig jelez, akkor itt. Azaz egy teszttel megfeleztük a potenciális betegek körét, és így felezgetve pl. 1024 katona esetén elég 10 teszt is. Igen ám, de a teszt elvégzése időigényes lehet. Ha mondjuk 3 napig tart, és mindig meg kell várnunk az előző teszt eredményét, hogy tudjuk, milyen vérmintákat kell összeönteni a következőhöz, akkor a beteg kiszűrése 30 napig fog tartani. Tudjuk-e úgy tervezni tesztek egy lehetőleg minél kisebb rendszerét, hogy azokat egyszerre elvégezve, bármilyen válaszokat is kapunk, a végén meg tudjuk mondani, ki a beteg? Itt segítenek a halmazok. Egy tesztet az határoz meg, hogy mely katonák vérmintáját tesszük bele. Azaz az alaphalmaz (a hadsereg) egy részhalmaza (a vizsgált katonák). Mit kell tudnia egy halmazrendszernek ahhoz, hogy az általa meghatározott tesztek megtalálják a beteget? Azt, hogy ha X katona a beteg, akkor másak legyenek a pozitív tesztek, mint ha Y katona a beteg (bárki is X és bárki is Y). De egy teszt pozitív, ha a beteg katona vérmintája belekerül. Azaz akkor lesz jó a halmazrendszer, ha az alaphalmaz (hadsereg) bármely két eleméhez (katonák) lesz egy olyan halmaz (vérteszt), ami pontosan az egyiket tartalmazza (az ilyen rendszereket szeparáló halmazrendszereknek nevezik). Kicsit talán meglepő módon ilyen nehezített esetben is pont ugyanannyi kérdésre (tesztre/halmazra) van szükségünk, mint a felezéses módszernél. Ez egy rég megoldott probléma, melynek sok (megoldott vagy megoldatlan) verziója van: több beteg van, akik közül meg kell találnunk egyet/mindet/a felüket. A tesztek néha adhatnak hibás választ. A hiba történhet véletlenül, vagy egy gonosz manó legfeljebb 5 teszt eredményét megváltoztathatja, stb. Ha a teszteket párhuzamosan kell elvégeznünk és nem támaszkodhatunk a korábbiak eredményére, akkor a feladat általában valamilyen halmazrendszeres problémára vezethető vissza.

És az igazság?

Az igazság „odaát”, esetleg „a kettő között” van. Mindenesetre az igazságot mindenképp egy közhely írja le, így a számunkra rendelkezésre álló közhelyek közül válasszuk a kettő közöttről szólót. Talán romantikus volna azt gondolni, hogy az extremális halmazrendszerekkel foglalkozó kutatók megengedhetik és meg is engedik maguknak, hogy a saját maguk által véletlenszerűen kitalált halmazrendszer-tulajdonságokat vizsgálják, örülnek egy-egy szép bizonyításnak, és bármilyen külső megfontolástól függetlenül oldogatják egymásnak és maguknak szánt matematikai fejtörőiket. A másik véglet szerint csak a való életből származó problémák matematikai modelljeinek problémáival (mint a fent leírt hibajavító kódok vagy a kereséselméleti problémák) kellene időnket tölteni: ez a variáció különösen hasznos lehet a tudomány belső logikájára kevésbé érzékeny pályázati kiírások esetén, ha meg szeretnénk magyarázni, miért van mindenképp szükség az extremális halmazrendszerek témakörének kutatására. De az „igazi válasz” pont ezen a nehezen megfogható és emiatt nehezen elmagyarázható belső logikán alapul: a közvetlenül alkalmazható és az absztrakt nonszensz problémák helyett a legtöbb kutatott kérdés vagy egy más alterületen már megvizsgált probléma analógja, vagy két látszólag különböző téma kapcsolatát kutatja, vagy egy megoldatlan problémát vezet vissza egy másikra. Mindenesetre kutatók kézirataik bevezetőjében valami ilyesmivel motiválják az általuk éppen bevezetett kérdést: ha érdekesnek, kutatásra érdemesnek találtuk azt, meg azt, meg azt a problémát (és hát azok már megjelentek folyóiratokban!), akkor nyilvánvalóan érdekes ez is, hiszen hasonló azokhoz, vagy következik azokból, vagy valahogyan mindenképp köze van hozzájuk. (Aztán a tudományos folyóiratok szerkesztői által kijelölt független bírálók eldöntik, hogy tényleg olyan nyilvánvaló-e az a kapcsolat, és tényleg érdekes-e az új kérdés.) Zárásként nézzük meg, hogy milyen motivációval vizsgálták az ebben az írásban szereplő extremális halmazrendszeres problémákat.

Erdős Pál 1945-ben bizonyította Sperner baloldali angolok klubjairól, azaz antiláncokról szóló tételének egy általánosítását. Az általánosítás a bugyuta verzióban úgy fogalmazható meg, hogy most megengedhető, hogy egy klub egy másiknak „előszobája” legyen, ez a másik egy harmadiknak, és így tovább, de a leghosszabb ilyen „kerüljünk egyre beljebb” procedúra sem lehet hosszabb 7 állomásnál. Halmazos megfogalmazásban ez úgy hangzik, hogy a halmazrendszer nem tartalmazhat 8 egymásba ágyazott halmazt, azaz egy 8 hosszú 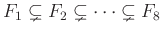$F_1 \subsetneq F_2 \subsetneq \dots \subsetneq F_8$ láncot. Mennyi a lehető legtöbb kiválasztható halmaz ezen új szabályok esetén? (Erdős persze nem csak 8, hanem tetszőleges pozitív egész szám esetén megadta a kérdésre a választ.) Azt gondolhatnánk, hogy Erdős cikkében arra hivatkozik, hogy Sperner tételét általánosítja. De Sperner eredménye meg sincs említve a cikkben, amelynek címe On a lemma of Littlewood and Offord, ugyanis a két brit matematikus (Littlewood a Royal Society tagja volt és Offorddal közös eredményük idején a London Mathematical Society elnöke) egy analízisbeli eredményét javította meg. Azaz a matematika egyik területén felmerült kérdést oldott meg a matematika egy nagyon különböző másik területén bizonyított eredménnyel.
Miért érdekelték deBruijnt és Erdőst az – általam a félénk tinderezők klubjainak nevezett – pontosan 1-metsző halmazrendszerek? Bár cikkük címe On a combinatorial problem (egész pontosan On a combinatioral problem, mert a gondos szerkesztők figyelmén néha már akkor is átcsúszott, ha a szerzők felcseréltek pár betűt), de motivációjuk geometriai volt: az euklideszi síkon is igaz, hogy két különböző egyenesnek legfeljebb egy metszéspontja van, de a párhuzamos egyeneseknek nincs egy sem, így egyenesek egy tetszőleges családja nem feltétlenül alkot pontosan 1-metsző rendszert. Az úgynevezett projektív síkon viszont bármely két egyenes metszi egymást. DeBruijn és Erdős ezen projektív síkok tulajdonságait vizsgálta, és tételük egyik következménye, hogy egy ilyen projektív síkon bárhogy is veszünk néhány pontot, az általuk meghatározott egyenesek száma legalább annyi lesz, mint ahány pontból kiindultunk – kivéve, ha egyetlen egyenes néhány pontjából indultunk eredetileg. (Ez az állítás igaz a mi euklideszi síkunkban is.) Azaz megint arra láttunk példát, hogy a kombinatorika eszköz a matematika egy másik területén felmerült probléma vizsgálatához.
Végül nézzük az uniform metsző halmazrendszerekről szóló Erdős-Ko-Rado tétel történetét. Ha csak a cikket olvassuk, meglepődve tapasztalhatjuk, hogy bár Erdős meg sem említette Sperner tételét, amikor annak egy általánosítását bizonyította, most két szerzőtársával pont ezt a tételt említik kiindulópontként. („This note contains analogues of this result.”) A valóság azonban még ennél is kicsit viccesebb: Erdős, Ko és Rado 1938-ban bizonyították eredményeiket, de úgy értékelték, hogy azok nem elég érdekesek a tudományos közösség számára, így nem publikálták őket. A végül 23 évvel később megjelent cikknek jelenleg (2019. január 26.) 1161 idézője van a Google Scholar szerint.