Szabaduló tanterem

Nagyon szeretek Rátz László Vándorgyűlésekre járni. Minden évben az a nyár egyik fénypontja. Szeretem a társaságot, a szellemi kihívásokat és a rengeteg új ötletet, másfajta megközelítést, amiktől mindig gazdagabbnak érzem a tudásomat az előadássorozat végére. Tátott szájjal hallgattam Számadó László cirkuszi ötleteit és zseniális kivitelezését, nagyon tetszett a Gamification alapú értékelésről szóló előadás és Danka Miklós algoritmikus gondolkodással kapcsolatos ötletei is lenyűgöztek. Csordás Péter Játékos matematika című előadásán is sok új ötletet hallottam, hihetetlenül pörgős, jól követhető előadás volt.

Ezekben az előadásokban volt valami közös. Mindegyik mögött ott áll az a gondolat, ami szinte mindannyiunkat foglalkoztat, hogyan motiváljuk a gyerekeket. Hogyan vegyük rá őket arra, hogy ők maguk, egy belső késztetés miatt akarjanak az órán, sőt azon kívül is dolgozni.

Elmesélem, milyen trükkökhöz szoktam én folyamodni, ha munkára szeretnék bírni egy osztályt.

Versenyző típus vagyok, mindig is az voltam. Az a típusú ember vagyok, aki nem azt mondja a saját gyerekeinek, hogy gyertek, induljunk, hanem azt: Verseny a kocsiig? Szóval az egész életemet áthatja ez a versenyszellem. Persze tanulókat versenyeztetni mindig szoktam, nagy lelkesen, teljes erőbedobással. De vajon mit kezdhetek azokkal a gyerekekkel, akik nem járnak matek versenyekre? Azon gondolkodtam, hogyan tudnám mégis becsempészni a versenyzést a hétköznapokba.

A versenyzési mániám mellett csoportmunka mániám is van. Nagyon fontosnak tartom, hogy a gyerekek gyakran dolgozzanak csoportban, mert számtalan sok előnye van. Ezeket biztosan mindenki tudja, most nem részletezem. Ezt a két mániámat gyúrtam össze.

Ekkor jött a szuper ötlet, szabaduló szobák. Nem az én ötletem persze, de remekül alkalmazható osztályteremben is. Hisz az egész lényege az, hogy meg kell oldani egy csomó feladatot ahhoz, hogy a végén nyerjünk. Bevittem az iskolába, innen az elnevezés, szabaduló tantermek. Egy ilyen óra felépítése hasonlít az eredeti szabaduló szobákhoz. Van egy kerettörténet, amit az óra elején felolvasok a gyerekeknek. A sztori kitalált, nálam általában meg kell menteni a világot, mert valami megtámadott minket. Ha 40 perc alatt sikerült, még Chuck Norris is büszke lesz ránk, ami lássuk be, menő dolog. Kiosztom a feladatokat és kezdődhet a verseny.

A versenyek önellenőrzős versenyek. Minden feladathoz tartozik egy szám, egy úgynevezett titkos kódhoz tartozó első, második… szám. Ez a szám vagy az eredménye a feladatnak, vagy annak valahányszorosa…, vagy az is lehet, hogy ha ezt kaptad, akkor ez a titkos kódhoz tartozó egyik számod, ha meg azt kaptad, akkor meg az. A lényeg, hogy egész számok legyenek. Ha a gyerekek minden feladatot megoldottak, van annyi egész számuk, ahány feladat volt. Ha ezeket a számokat összeadják és az eredménnyel elosztják a feladatsor végén található nagy számot, akkor (feltéve, hogy hibátlanul dolgoztak) egész szám lesz a hányados. Ez a titkos kód.

Ebben nyilván trükköztem, hisz a feladatsor végén álló szám két „nagy” prímszám szorzata, amit nemes egyszerűséggel nem lehet feltörni 40 perc alatt, kiküszöbölve ezzel az egyéb irányú kódfejtéseket. Az egyik az összeadás során kijött szám, a másik a titkos kód.

A versenynél nagyon fontosnak tartom, hogy a gyerekek ne csak egymás ellen versenyezzenek, ne a másikat kelljen legyőzni. Így az óráimon általában vagy az idő ellen versenyeznek, vagy valami közös cél éléréséért.

Mik a jó közös célok, hisz mindenki másnak örül?

Erre a következő megoldást adtam. Adott egy feladatsor, ha sikerül hibátlanul megoldani, tehát megmentették a világot ☺, minden gyerek 2 ajándékot választhat. Vagy kér egy plusz-t (4 darab egy ötös) vagy kér $+1$ pontot (ezek a pontok dolgozatnál felhasználhatók, ha csak ennyi hiányzik a jobb jegyhez, egy dolgozatnál max. 2 pont vehető igénybe) vagy kér egy cukrot a világ egyik legfinomabb cukrából (ezt én veszem, 1 kg 1000 Ft, sokáig elég). Ez a három ajándék természetesen tetszőlegesen kombinálható.

Hihetetlen izgalmas látni azt is, ki mit választ. A gyerekek törik a fejüket, milyen jó lett volna a múltkori dolinál az a plusz egy pont vagy már van két plusza, ha most kér kettőt, hazavihet ma egy ötöst. Vagy csak egyet kér és akkor még egy cukrot is ehet, úgyis játszunk még ilyet és a cukor tényleg világbajnok. És persze van itt még egy fontos adalék is, ilyenkor a gyerekek élhetnek a szabad választás jogával, ami szerintem szintén nagyon építő és valljuk be, jól is esik a sok kötelező feladat mellett.

Milyen a jó feladatsor?

Ez már nehéz ügy. Hiszen mindenkinek dolgozni kell, olyat nem lehet csinálni, hogy a legügyesebb mindent megold, a többiek meg „ingyen” ajándékhoz jutnak. Kell tehát egy olyan feladatsor, amit nem tud egyedül megcsinálni még a legügyesebb sem. Illetve persze meg tud, de akkor kicsúszik az időből és senki nem nyer semmit. Többféle módszert is kidolgoztam erre a dilemmára.

1. ötlet – Szabaduló szoba, csoportmunkában

Összeállítok egy 10 feladatból álló feladatsort, mindegyikben három feladat van. A feladatsorban egyre nehezednek a feladatok, az utolsó egy-kettő tényleg nehéz. Ez persze az osztálytól függ, kinek mi a nehéz. A csoportokat én állítom össze. Már előző óra végén jelzem, hogy a következő órán ilyet játszunk és ismertetem a csapatokat, így a gyerekek már összetolt padokkal, csoportokra szétbontva várnak engem a következő óra elején. Ez az ő érdekük, hiszen ha az órán csinálják meg, kevesebb idejük marad, és esetleg emiatt nem sikerül kijutni a szabaduló tanteremből.

Az óra elején mindenkinek kiosztom a feladatokat, minden gyerek minden feladatot megkap. A csoport feladata, hogy szétosszák egymás között a munkát és adott esetben segítsék vagy ellenőrizzék is egymást. És akkor elkezdődik a munka.

Mindig megígérem, hogy nem segítek. Ritkán tartom be. Nagyon egyszerű oka van, iszonyatosan izgulok. Nehéz dolog jó feladatsort összeállítani. Olyat, ami megoldható 40 perc alatt, de nem könnyen. Szóval sétálgatok a teremben és ha valaki nagy bajban van, picit segítek. Sokszor az is elég, ha csak bólintok vagy mosolyogva annyit mondok, jó lesz, csak így tovább.

Akiknek az utolsó szám osztásakor a hányados egész szám, büszkén jönnek és mutatják, hogy kijutottak. És akkor kezdődik a fent említett ajándékválasztás.

Mi értelme van egy ilyen feladatsornak, hisz a gyerekek nagy része csak pár feladattal foglalkozott az óra során?

Erre több válasz is adható. Például, hogy a legügyesebb, amúgy országos bajnok is lássa, ő kevés egyedül, szüksége van akár az osztály leggyengébb tanulójának a munkájára is. Hisz csak együtt sikerülhetett. És ezzel párhuzamosan a gyengék is megélik azt, hogy nélkülözhetetlenek voltak. Ez remek érzés, mindenkinek jól esik.

De van olyan is, hogy azt mondom, az első nyolc feladatból egy feladat benne lesz a TZ-ben, más számokkal. Akkor mindenki megoldhatja az összes feladatot, hisz a feladatsor hazavihető. Sokszor látom, hogy a következő óra elején egymásnak magyarázzák a feladatokat, ami szintén klassz dolog.

2. ötlet – Szabaduló szoba, kooperatív csoportmunkában

Összeállítok egy 25–40 feladatból álló feladatsort, témája válogatja, mikor mennyit. Ebben a feladatsorban is nehezednek a feladatok és itt is minden gyerek megkap minden feladatot. A gyerekek osztják be egymás között, ki melyik feladatot csinálja meg, illetve ki kit ellenőriz. Mindenki lázasan dolgozik. A feladatok eredményeit a táblára írják, aki ellenőrizte, kipipálja, hogy egyértelmű legyen, hogy melyik feladat hibátlan (elméletileg). Miután minden feladatot megoldottak, a megoldás a fenti esetnek megfelelően működik. Összeadják a számokat, elosztják a kapott „nagy” számot az eredménnyel és az így nyert hányados a titkos kód. Ha ez egész szám, sikerrel jártak.

Kicsiknél (5–6. osztály) néha könnyítek, én ellenőrzöm a feladatokat, így fennáll a javítás lehetősége.

Ezek nagyon pörgős órák, hangosak a gyerekek, rohangálnak, beszélgetnek, egymásnak segítenek. Aztán beáll a néma csend, mindenki lázasan dolgozik, majd újra kavalkád és fergeteges ünneplés a végén, ha sikerült.

Munkabefektetés

Persze rengeteg munka előzi meg az ilyen órákat. Nagyon kell ismerni a csoportot, osztályt, hogy jól eltaláljuk a feladatok mennyiségét és nehézségi szintjét. Ki kell találni vagy össze kell vadászni rengeteg feladatot figyelve arra, hogy az eredmények összege a végén egy nagyobb (legalább négyjegyű) prímszám legyen, beírni a gépbe, mindet hibátlanul megoldani előre, és persze ki kell találni egy fedősztorit is, hogy az óra alaphangulata meglegyen.

Egy ilyen órát előkészíteni legalább 2–3 óra, mégis azt gondolom, megéri. Nagyon élvezik a gyerekek, és rengeteg pozitívuma van a matek feladatok megoldásán felül. Minden ilyen óra végén többen is odajönnek és megkérdezik, mikor játszunk ilyet megint. Pedig ez nem játék, nagyon nem az. Klassz, hogy mégis annak élik meg.

Segítségképp összeállítottam pár feladatsort. Ezeket 16–18 fős csoportok számára ajánlom.

Szabaduló tanterem – Algebrai kifejezések 8. osztály

Egy szabaduló szobában vagy, a kerettörténet a következő:

Gonosz poliGNÓMok támadták meg a Földet és el akarják pusztítani. Csupán 40 perced maradt, hogy megoldd az alábbi feladatsort, megfejtsd a négyjegyű kódot és bejuss vele a titkos irányító központjukba, amitől ők mindahányan garantáltan szörnyethalnak. Mentsd meg a világot!

1. Húzd alá az alábbi kifejezések közül az egyenlőket!

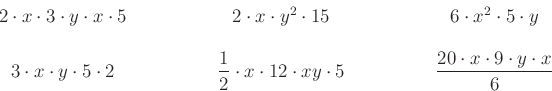
$\begin{displaymath}\begin{array}{ccc} \qquad 2\cdot x\cdot 3\cdot y\cdot x\cdot... ...d \dfrac{20\cdot x\cdot 9\cdot y\cdot x}{6}\qquad \end{array}\end{displaymath}$

Hány darabot találtál? Szorozd meg a darabszámot 15-tel, ez a kódhoz szükséges első szám!

2. Számold ki az alábbi kifejezések helyettesítési értékeit, ha 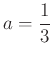$a=\dfrac{1}{3}$ és $b=-1$ !

a) $\left(12a+16b \right)-\left(6a-9b \right)=$

b) $\left(5a^{2}-3b^{2} \right)-\left[ \left(a^{2}-2ab-b^{2} \right)-\left(5a^{2}-2ab-3b^{2}\right)\right]=$

Szorozd össze a fenti két eredményt, ez lesz a kódhoz szükséges második szám!

3. Bontsd fel a zárójeleket és végezd el a lehetséges összevonásokat! Határozd meg a kifejezés helyettesítési értékét, ha 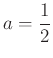$a=\dfrac{1}{2}$ !

$\displaystyle \left(4a^{3}-2a^{2}+5a-1\right)+\left(-2a^{3}+3a^{2}-11a-4\right)-\left(3a^{3}+a^{2}-6a+7\right)-5a=$

Határozd meg, melyik két egész szám között van a végeredmény! Szorozd össze ezt a két számot, ez lesz a kódhoz szükséges harmadik szám.

4. Végezd el a következő szorzásokat és vonj össze, ahol csak lehet!

a) $\left(2x+4\right)\left(3x+5\right)=$

b) $\left(x-7\right)\left(2-6x\right)=$

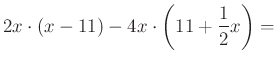
c) $2x\cdot \left(x-11\right)-4x\cdot \left(11+\dfrac{1}{2}x\right)=$

Add össze az eredményként kapott algebrai kifejezéseket, az összeget szorozd meg 37-tel, így megkapod a kódhoz szükséges negyedik számot!

5. Párosítsd össze a következő algebrai kifejezéseket!

$\begin{displaymath}\begin{array}{cc} \begin{array}{c} (a+2)^2\\ [4mm] (2a-1)^... ...+1\\ [2mm] 2a^2+2a+4\\ [2mm] a^2-4a+4 \end{array}\end{array}\end{displaymath}$

Add össze azokat a kifejezéseket, amiknek nincs párja. Az így kapott eredmény 19-szerese lesz a kódhoz szükséges ötödik szám!

6. Pótold a hiányos kifejezéseket úgy, hogy teljes négyzetet kapj!

a) $4x^{2}+\ldots\ldots\ldots\ldots+49$

b) $81x^{2}+\ldots\ldots\ldots\ldots+1$

c) $\dfrac{1}{25}x^{2}+\ldots\ldots\ldots\ldots+100$

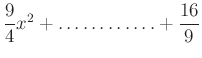
d) $\dfrac{9}{4}x^{2}+\ldots\ldots\ldots\ldots+\dfrac{16}{9}$

Add össze az általad beírt kifejezéseket és határozd meg az összeg helyettesítési értékét, ha 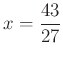$x=\dfrac{43}{27}$ ! Az így kapott szám lesz a kódhoz szükséges hatodik szám!

7. Oldd meg az alábbi egyenleteket!

a) $\left(2x+3\right)^{2}=\left(x-7\right)^{2}+3\left(x^{2}+4\right)$

b) $\left(3x+4\right)^{2}-100=9\left(x-2\right)\left(x+2\right)$

c) $\left(x+9\right)\left(2x+14\right)\left(8-x\right)=0$

Szorozd össze a fenti egyenletek minden megoldását, így megkaptad a kódhoz szükséges hetedik számnál 1-gyel kisebb számot!

8. Határozd meg, a változók mely értékeire nem értelmezhetők a következő algebrai kifejezések!

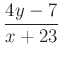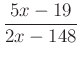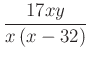
a) $\dfrac{4y-7}{x+23}$ b) $\dfrac{5x-19}{2x-148}$ c) $\dfrac{17xy}{x\left(x-32\right)}$

Add össze a feladatban szereplő „tilos” értékeket, így megkapod a kódhoz szükséges nyolcadik számot!

9. Oldd meg a következő egyenleteket a racionális számok halmazán!

a) $2\left(x+3\right)-5\left(3x-4\right)=4-2\left(7-x\right)$

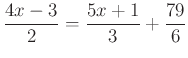
b) $\dfrac{4x-3}{2}=\dfrac{5x+1}{3}+\dfrac{79}{6}$

Szorozd össze a fenti két megoldást, így megkapod a kódhoz szükséges kilencedik számot!

10. Oldd meg a következő egyenletet!

$\displaystyle x\left(x+2\right)-3x\left(8-x\right)=2x\left(x-11\right)+50$

A kódhoz szükséges tizedik szám, ha nincs az egyenletnek megoldása 19, ha egy megoldása van, akkor az eredmény duplája és ha két megoldása van, akkor a megoldások összege.

Add össze a fenti feladatok végeredményeit és oszd el ezzel a számmal a $10\,887\,979$ számot!

Ha a fenti feladatokat hibátlanul oldottad meg, hányadosként egy egész számot kapsz.

Ez a szám a titkos kód, amellyel bejutsz a poliGNÓMok irányító központjába. Gratulálok, Te vagy a Földön az egyetlen ember, akire még Chuck Norris is felnéz!

Feladatok – a négyzetgyökvonás azonosságai, 10. osztály

Egy szabaduló szobában vagy. A kerettörténet a következő:

Egy műkincs tolvaj nyomába eredtél, és eljutottál a titkos földalatti kazamata rendszerébe, ahol az ellopott kincseket őrzi. Oldd meg az alábbi feladatokat, hogy megkapd azt a négyjegyű kódot, amivel bejutsz a páncélterembe. Vigyázz, csak 40 perced van rá!

1. Számold ki, hogy milyen számjegy áll a következő törtek tizedes tört alakjában a tizedes vessző utáni 2016. helyen!

a) $\dfrac{27}{24}$ b) $\dfrac{31}{6}$ c) $\dfrac{3}{7}$

Add össze a fenti feladatok végeredményeit és ennek a számnak a háromszorosa lesz a kódhoz szükséges első szám!

2. Döntsd el, hogy mely állítások igazak és melyek hamisak!

a) Két racionális szám különbsége mindig racionális szám.

b) Két irracionális szám szorzata mindig irracionális szám.

c) Egy racionális és egy irracionális szám összege mindig irracionális.

d) Van olyan irracionális szám, amelynek a reciproka racionális.

A fenti állítások közül minden igaz állítás 63, minden hamis állítás 27 pontot ér. Add össze a fenti négy állításért járó pontokat, így megkapod a kódhoz szükséges második számot!

3. Határozd meg, melyik két egész szám között van a következő szám: ${23-2\sqrt6}$ !

Szorozd össze ezt a két számot, ez lesz a kódhoz szükséges harmadik szám!

4. Keresd meg és karikázd be az egyenlőket az alábbi kifejezések között!

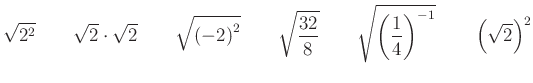
$\displaystyle \sqrt{2^{2}} \qquad \sqrt2\cdot \sqrt2 \qquad \sqrt{\left(-2\righ... ...}\qquad \sqrt{\left(\dfrac{1}{4}\right)^{-1}}\qquad \left(\sqrt{2}\right)^{2}$

Számold össze, hány számot karikáztál be! Ennek a tízszerese lesz a kódhoz szükséges negyedik szám!

5. Végezd el a következő műveleteket!

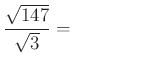a) $\sqrt{2025}=\qquad\qquad$	b) $\dfrac{\sqrt{147}} {\sqrt3}=\qquad\qquad$	c) $\left(\sqrt5\right)^{3}\cdot \sqrt5=\qquad\qquad$
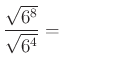d) $\dfrac{\sqrt{6^8}}{\sqrt{6^4}}=\qquad\qquad$	e) $\sqrt{8^{5}}\cdot \sqrt{8}=\qquad\qquad$	f) $\sqrt2\cdot \left(\sqrt{32}-\sqrt2\right)=\qquad\qquad$

Add össze a fenti feladatok végeredményeit és ez lesz a kódhoz szükséges ötödik szám!

6. A műveletek elvégzésével döntsd el, melyik szám a nagyobb!

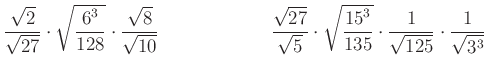
$\displaystyle \dfrac{\sqrt2} {\sqrt{27}}\cdot \sqrt{\dfrac{6^{3}}{128}}\cdot \d... ...dfrac{{15}^{3}}{135}}\cdot \dfrac{1}{\sqrt{125}}\cdot \dfrac{1}{\sqrt{3^{3}}}$

Vedd a kisebb szám ezerszeresét, ez lesz a kódhoz szükséges hatodik szám!

7. Végezd el a műveleteket!

a) $\sqrt3\cdot \left(\sqrt{12}+\sqrt{75}-\sqrt3\right)=$

b) $\left(\sqrt{80} -\sqrt{20}+\sqrt{45}\right)\cdot \sqrt5=$

c) $\left(\sqrt{23}+\sqrt7\right)\cdot \left(\sqrt{23} -\sqrt7\right)=$

d) $\left(4\cdot \sqrt2+2\sqrt7\right)\cdot \left(4\cdot \sqrt2 -2\sqrt7\right)=$

Add össze a műveletek végeredményeit, így megkapod a kódhoz szükséges hetedik számot!

8. Végezd el a következő műveleteket!

a) $\sqrt{7+\sqrt{24}} \cdot \sqrt{7-\sqrt{24}} =$

b) $\sqrt{\sqrt{19} -\sqrt3} \cdot \sqrt{\sqrt{19}+\sqrt3}=$

c) $\sqrt{\sqrt{31}-\sqrt6}\cdot \sqrt{\sqrt{31}+\sqrt6}=$

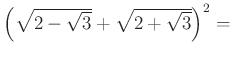
d) $\left(\sqrt{2-\sqrt3}+\sqrt{2+\sqrt3}\right)^{2}=$

Vedd az eredmények összegének négyszeresét, így megkapod a kódhoz szükséges nyolcadik számot!

9. Számítsd ki a következő kifejezések értékét!

a) 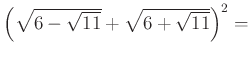$\left(\sqrt{6-\sqrt{11}}+\sqrt{6+\sqrt{11}}\right)^{2}=$

b) 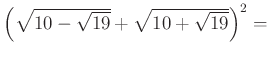$\left(\sqrt{10-\sqrt{19}}+\sqrt{10+\sqrt{19}}\right)^{2}=$

Ha a két eredmény összegét megszorzod 23-mal, megkapod a kódhoz szükséges kilencedik számot!

10. Oldd meg az alábbi egyenleteket!

a) $\sqrt{5-\sqrt{x}} \cdot \sqrt{5+\sqrt{x}} =2$

b) $\left(\sqrt{8-\sqrt{y}}+\sqrt{8+\sqrt{y}}\right)^{2}=30$

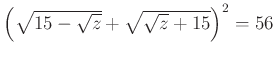
c) $\left(\sqrt{15-\sqrt{z}}+\sqrt{\sqrt{z}+15}\right)^{2}=56$

Határozd meg az $x+y+z$ értékét, ez a kódhoz szükséges tizedik szám.

Add össze a fenti feladatok végeredményeit és oszd el ezzel a számmal a $10\,540\,393$ számot!

Ha a fenti feladatokat hibátlanul oldottad meg, hányadosként egy egész számot kapsz. Ez a szám a titkos kód, amellyel bejutsz a páncélterembe. Sikerült? Gratulálunk! Gyere és nézd meg a kincseket! ☺

Mentsd meg a világot! – vegyes feladatok, 5. osztály, kooperatív csoportmunka

Gonosz geotrollok támadták meg a világot és el akarják pusztítani a Földet! Ezeket a szörnyeket csak a galaktikus zsoldoshadsereg győzheti le, akik nagyon drágán dolgoznak, 1000 aranyért pusztítják el az összes geotrollt.

A feladatotok, hogy legfeljebb 40 perc alatt az egész csoport közösen összegyűjtsön 1000 aranyat, amiről a zsoldoshadsereg a galaktikus távközlési hálózaton keresztül természetesen azonnal értesül, automatikusan dolgozni kezd, így a segítségükkel megmenthetitek a világot. A feladatsor hibátlan megoldása során 1200 aranyat gyűjthettek. A táblára felragasztott papírokra írhatjátok fel a feladatok végeredményeit, amit én pipálgatok majd, ha hibátlan.

Ha sikerül 1000 aranyat összegyűjtenetek, megmentitek a világot és mivel életben maradtunk, mindenkinek adok 2-2 jutalmat. Ha minden feladat hibátlan, 3-t választhattok.

1. Hány cm hosszú az a szalag, amelyből 11 és fél m-t és 37 dm-t levágva egy 320 cm-es darab marad? (20 arany)

2. Egy fonalgombolyagból a cica leszakított 17 cm-t, majd 270 mm-t, ezután 5 dm-t és még 56 cm-t. Így a fonálból 500 mm maradt. Add meg méterben a fonál eredeti hosszát! (20 arany)

3. A Tisza tavaszi áradásakor 125 km hosszan olyan magas volt a víz szintje, hogy a töltést ezen a szakaszon homokzsákokkal kellett megerősíteni. Hány homokzsákot raktak le, ha egy homokzsák 80 cm hosszú és 4 sort tettek egymásra? (30 arany)

4. Egy kiránduláson az első óra alatt 5 és fél km-t tettek meg a diákok, a második órában 4800 m-t, a harmadikban az első két óra alatt megtett út hosszának a felét. Hány métert gyalogoltak aznap a kirándulók? (20 arany)

5. Egy emelődaru teherbírása 4 tonna. Fel tud-e emelni egyszerre 7 db 150 kg-os és 6 db 400 kg-os betontömböt? (20 arany)

6. Egy lázcsillapító tabletta tömege fél gramm. Egy dobozban 20 tabletta van, egy kartonban 50 doboz, és egy raklapon 1500 karton fér el. Hány tonna gyógyszert szállít az a kamion, amelynek a csomagtartójába 12 raklapnyi áru fér el? (30 arany)

7. Egy üveg meggybefőtt tömege 680 gramm. Mennyi ebből a meggy tömege, ha az 20 grammal több, mint az üvegé? (30 arany)

8. Egy 1375 m hosszú alagúton halad át a 125 m hosszú vasúti szerelvény. Hány percig tart a teljes szerelvény áthaladása, ha másodpercenként 25 métert tesz meg? (30 arany)

9. Ákos, Barnus és Csaba párosával ráálltak a mérlegre. Ákos és Barnus együtt 84 kg, Barnus és Csaba együtt 92 kg, Ákos és Csaba együtt 94 kg volt. Mekkora a fiúk tömege külön-külön? (30 arany)

10. Anya farsangi fánkot süt, egy és fél perc alatt sül ki 4 darab a serpenyőben. Hány fánkot süt másfél óra alatt? (30 arany)

11. Hány percet töltöttél az iskolában, ha 7:48-kor érkeztél és 13:12-kor indultál haza? (20 arany)

12. Egy lift ajtaján a következő szöveg olvasható: 4 személy (max. 400 kg) részére. A liftre várakozó Antal 124 kg-os. Megérkezik Bendegúz és két barátja. Hármójuk közül Bendegúz a legnehezebb, ő 92 kg-os. Legfeljebb hány kg az együttes súlyuk? Beszállhatnak-e mind a négyen a liftbe? (30 arany)

13. Janka hetente egyszer elmegy úszni. A medence hossza 33 méter. Minden alkalommal legalább 15, de legfeljebb 20 medencehosszt úszik. Hány métert úszik Janka egy év (365 nap) alatt? (30 arany)

14. Az osztálykirándulásra minden tanulónak 12 850 Ft-ot kell befizetni. Mennyi pénz gyűlik össze, ha 34 tanuló jár az osztályba? (20 arany)

15. Balabárban 1 kéktúra és 1 zöldtúra annyit ér, mint 4 zöldtúra és 3 pirostúra. Továbbá 10 zöldtúra annyit ér, mint 4 zöldtúra és 1 kéktúra. Hány zöldtúra ér annyit, mint 1 kéktúra? Hány zöldtúra 1 pirostúra? (30 arany)

16. Ha 3 darab hagyma ugyanannyiba kerül, mint 2 db alma, akkor melyik a drágább: 11 darab alma és 5 darab hagyma vagy 11 darab hagyma és 5 darab alma? (30 arany)

17. Hány cm-es az a fiú, akinek a testmagassága 120 cm és még a testmagasság felének a harmada? (30 arany)

18. Összesen 13 db 10 és 20 forintos érmével fizettünk ki 210 Ft-ot. Melyik érméből hány darabot használtunk fel? (40 arany)

19. A gyümölcsösben 160 almafán 75 kg, 142 almafán 105 kg és 85 almafán pedig 160 kg volt az átlagtermés. Egy cég 50 tonna alma felvásárlására kötne szerződést. Az adatok ismeretében számold ki, rendelkezésünkre áll-e a kérdéses mennyiség? (20 arany)

20. 27 darab teljesen egyforma üvegből 9 db tele van mézzel, 9 db féli van, a többi üveg üres. Hogyan tudjuk az üvegeket 3 dobozba úgy elhelyezni, hogy mindegyik dobozban azonos mennyiségű méz legyen? (20 arany)

21. Három üvegben 6 liter folyadék van. Ha az elsőből kiöntünk 1 litert, a másodikból 8 dl-t, a harmadikból 6 dl-t, akkor mindegyik üvegben ugyanannyi marad. Hány deciliter volt az egyes üvegekben eredetileg? (30 arany)

22. Ha 5 kiskutya 3 perc alatt 1 liter tejet iszik meg, akkor 101 kiskutya 1 óra alatt hány liter tejet iszik? (40 arany)

23. Egy falióra 9 másodperc alatt üti el a tíz órát. Hány másodperc alatt üti el az öt órát? (20 arany)

24. 5 darab egyforma, 20 cm hosszúságú, azonos minőségű gyertyát 5 perc időkülönbséggel meggyújtottunk. Az első gyertya meggyújtásától számítva hány perc telik el az ötödik gyertya teljes elégéséig, ha minden gyertya 1 mm-t fogy 1 perc alatt? (30 arany)

25. Hány perc telik el hajnali 4 óra 47 perctől másnap délután 15 óra 12 percig? (20 arany)

26. Hány óra van most, ha éjféltől ötször annyi idő telt el mostanáig, mint amennyi a teljes napból még hátra van? (30 arany)

27. Nyuszifül már megfestette a tojások negyed részét. Ha még két tojást festene, akkor már készen lenne a tojások harmadrészével. Hány tojást kell összesen megfestenie? (40 arany)

28. Torkos Mókus hétfőn megette a diók felét és még 1 diót. Kedden a maradék felét és még egy diót. Így szerdára már csak 10 szem diója maradt. Hány diója volt Torkosnak hétfőn reggel? (40 arany)

29. Használjuk ebben a feladatban a t: tucat (12); d: darab (1) és a p: pár (2) rövidítéseket! Végezd el a műveleteket, az eredményt p-ban add meg! (40 arany)

a) $\left(2~\text{t}-6~\text{d}\right)-\left(2~\text{t}-6~\text{p}\right)= \qquad \qquad \qquad \qquad \qquad ~\text{p}$

b) $\left(5~\text{p}+2~\text{d}\right)\cdot 3+\left(8~\text{p}-9~\text{d}\right)\cdot 2= \qquad \qquad \qquad \qquad ~\text{p}$

30. Az n a nap rövidítése; az ó órát jelent; a h a hét rövidítése. Végezd el a műveleteket! (30 arany)

a) $5~$ n $-3\cdot \left(1~\text{n}+7~\acute{\text{o}}\right)= \qquad \qquad \qquad \qquad \acute{\text{o}}$

b) $3\cdot \left(2~\text{h}+5~\text{n}\right)+2\cdot \left(3~\text{h}-4~\text{n}\right)= \qquad \qquad \qquad \qquad~\text{n}$

31. Végezd el a műveleteket! (30 arany)

a) $137~$ dm $+6~$ m $+2~$ km $= \qquad \qquad \qquad \qquad~$ dm

b) $29~$ cm $+13~$ m $+1200~$ mm $= \qquad \qquad \qquad \qquad \qquad~$ cm

32. Végezd el a műveleteket! (30 arany)

a) $\left(51~\text{perc}+4~\acute{\text{o}}\text{ra}\right)\cdot 5= \qquad \qquad \qquad \qquad \qquad \text{perc}$

b) $\left(3~\text{nap}+34~\acute{\text{o}}\text{ra}\right):2= \qquad \qquad \qquad \qquad ~\acute{\text{o}}\text{ra}$

33. Végezd el a műveleteket! (30 arany)

a) $60~$ kg $:60~$ dkg $= \qquad \qquad \qquad \qquad~$ g

b) $\left(3~\text{kg}+20~\text{dkg}\right):800~\text{g}=\qquad \qquad \qquad \qquad \text{g}$

34. Egy szoba magassága deciméter pontossággal mérve 29 dm. Legalább hány centiméter lehet a magassága? (20 arany)

35. Terka süteményt sütött. Harmadannyi áfonyást, mint málnást, és negyedannyi szamócást, mint málnást. Így éppen 2-vel több áfonyás süteményt sütött, mint szamócást. Hány süteményt sütött összesen? (40 arany)

36. Építettünk egy nagy kockát, majd pár kis kockát elvettünk belőle. Legkevesebb hány kis kocka hiányzik egy nagy kockához az alábbi testekből? (A képen látható alakzatok tömör alakzatok.) (30 arany)

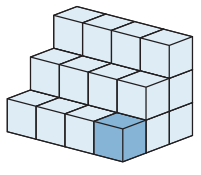
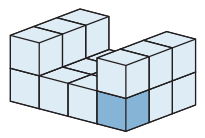
37. Egy szülinapi bálon 5 testvérpár vett részt. A tíz gyerek mind különböző életkorú (az életkorok egész számok), a legfiatalabb 5, a legidősebb 14 éves. Négy testvérpár két-két tagjának életkorát összeadva 15, 18, 19 és 26 az eredmény. Az ötödik testvérpár egyik tagja 10 éves. Hány éves a testvére? (40 arany)

38. Anna, Bori, Csilla, Dani és Elemér egy hosszú padra szeretnének leülni. Összesen hányféleképpen ülhetnek le egymás mellé, ha az azonos neműek nem ülhetnek egymás mellett? (40 arany)

39. Az éjjel Bogáncs minden ötödik, Pamacs minden hatodik, Bodri minden nyolcadik percben vakkantott egyet. A vakkantást mindhárom kutya 22 órakor kezdte. Reggel 7 óráig összesen hány alkalommal vakkantott egyszerre a három kutya ezen az éjszakán? (40 arany)

40. 1 alma, 1 körte és 1 barack közül Ági, Bori és Csilla megevett egy-egy gyümölcsöt. Arra a kérdésre, hogy ki melyiket ette meg a következőket válaszolták:

Ági: Az almát Csilla ette meg.

Bori: A körtét Csilla ette meg.

Csilla: Nem mondanak igazat, én sem az almát, sem a körtét nem ettem meg.

Tudjuk, hogy aki a barackot ette meg, nem mondott igazat. Melyik gyümölcsöt ki ehette meg? (50 arany)

Győzd le a matekorkokat! – 8. osztály, kooperatív csoportmunka

Gonosz matekorkok támadták meg a világot és el akarják pusztítani a Földet! Ezeket a szörnyeket csak a galaktikus zsoldos robothadsereg győzheti le, akiknek a beindításához egy titkos kód szükséges. A feladatotok, hogy legfeljebb 40 perc alatt az egész csoport közösen hibátlanul megoldja a következő feladatokat, megfejtsétek a kódot, amiről a zsoldos robothadsereg a galaktikus távközlési hálózaton keresztül természetesen azonnal értesül, automatikusan dolgozni kezd, így a segítségükkel megmenthetitek a világot.

1. Számold ki! Add össze az eredményeket!

a) $12^{2}=$ b) $15^{2}=$ c) $(-13)^{2}=$ d) $-14^{2}=$

2. Számold ki! Add össze az eredményeket!

a) $\sqrt{121} =$ b) $\sqrt{-64} =$ c) $-\sqrt{81} =$ d) $\sqrt{8^{2}+6^{2}} =$ e) $\sqrt{13^{2}\cdot 7^{2}}=$

3. Hány darab igaz állítás van az alábbiak között?

a) $\sqrt{256}\cdot \sqrt{144} = \sqrt{256\cdot 144}$

b) $\sqrt{25}\cdot \sqrt{25} = 5^{2}$

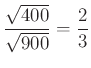
c) $\dfrac{\sqrt{400}} {\sqrt{900}} =\dfrac{2}{3}$

d) $\sqrt{625} :\sqrt{125} = \sqrt{625:125}$

e) $\sqrt{81} -\sqrt9 = \sqrt{81-9}$

f) $\sqrt{64}+\sqrt{49} = \sqrt{64+49}$

4. A téglalap egyik oldala 8 cm, a másik ennek a háromnegyede.

a) Számold ki a területét!

b) Számold ki az átlójának hosszát!

Számold ki a fenti két eredmény összegét!

5. A téglalap alakú parkon átlósan átvezet egy út, amelynek hossza 15 km. A park 9 km hosszú. Számold ki, milyen széles a park!

6. A derékszögű háromszög csúcsainak koordinátái $A(1;0)$ , $B(7;0)$ , $C(7;3)$ .

a) Számold ki a háromszög oldalainak hosszát! (Egy négyzetrács oldala 1 egység.)

b) Számold ki a háromszög területét!

Határozd meg a fenti eredmények összegét egészre kerekítve!

7. Egy derékszögű háromszög oldalainak mérőszámai pitagoraszi számhármast alkotnak. Mekkora a háromszög területe cm $^{2}$ -ben kifejezve, ha a kerülete 120 cm?

8. Egy rombusz oldala 17 cm hosszú, hosszabbik átlója 30 cm.

a) Számold ki a rombusz rövidebbik átlóját!

b) Számold ki a rombusz területét!

Határozd meg a fenti eredmények összegét!

9. Egy szimmetrikus trapéz alapjai 10 cm és 20 cm hosszúak, területe $180~$ cm $^{2}$ .

a) Számold ki a trapéz magasságát!

b) Számold ki a trapéz kerületét!

Határozd meg a fenti eredmények összegét!

10. Egy 5 cm sugarú kör középpontjától 13 cm-re lévő pontból érintőt húzunk a körhöz. Mekkora az érintőszakasz hossza?

11. Add meg a $d$ szakasz hosszának egészre kerekített értékét, ha $d$

a) a 12 cm oldalú négyzet átlója

b) a 16 cm átlójú négyzet oldala

c) a 32 cm oldalú szabályos háromszög magassága

Számold ki a fenti három eredmény összegét!

12. Egy húrtrapéz alapjainak hossza 24 cm és 16 cm, a magasságának hossza pedig 12 cm. Számítsd ki a trapéz szárainak hosszát! Vedd az eredmény százszorosát és kerekítsd egészre!

13. Egy $2{,}6$ méteres gerendát döntöttünk a falhoz. A gerenda éppen a fal tetejéhez támaszkodik, az alja pedig 132 cm-re van a faltól. Milyen magas a fal?

14. Számold össze, hogy az $a$ , $b$ , $c$ oldalakkal megadott háromszögek közül hány derékszögű háromszög van!

$a$	12	60	10	13	7	33	11	21	14
$b$	35	175	22	84	23	56	6	20	16
$c$	37	185	24	85	25	65	12	28	35

15. Az $ABCD$ húrtrapéz oldalainak hossza: $AB=5$ cm; $BC=2{,}5$ cm, $CD=2$ cm és $DA=2{,}5$ cm. Számold ki a trapéz magasságának és a trapéz kerületének a szorzatát!

16. Két fa között $1{,}5$ méter magasságban kifeszítettünk egy 10 méter hosszú ruhaszárító kötelet. A közepére ráakasztottunk egy száradó inget, amely 80 cm-re lóg le a kötél szintjétől. A kötél a ráakasztott vizes ing súlya miatt 4 cm-t megnyúlt. Milyen magasan lesz ekkor a száradó ing alja a talajtól? Kerekítsd az eredményt cm-re!

17. Kerítést szeretnénk készíteni az $924~$ m $^{2}$ területű, derékszögű háromszög alakú zöldséges kertünk köré. A kert 33 méter hosszúságú befogója mentén már elkészültünk vele. Milyen hosszú kerítést kell még készíteni, ha teljesen körbe akarjuk keríteni a kertet?

18. Egy 15 cm sugarú körbe egy 18 cm-es húrt rajzolunk. Milyen távolságra van ez a húr a kör középpontjától?

19. Géza úgy készített deltoidot, hogy egy 5 cm és 12 cm oldalú téglalapot az egyik átlója mentén kettévágott, és a két részt összeragasztotta. Milyen hosszú az így kapott deltoid rövidebb átlója? Válaszodat cm-re kerekítve add meg!

20. Egy szabályos háromszög magassága 7 cm. Számítsd ki egy középvonalának hosszát! Válaszodat cm-re kerekítve add meg!

21. A libegő szintkülönbsége 262 m, a vízszintesen mért hossza 1040 méter. Mennyi idő alatt érünk fel a pálya tetejére, ha az ülések sebessége $5{,}4~$ km $/$ h? (A menetidőt percre kerekítve add meg!)

22. Hány olyan rácspont van, amelynek az origótól való távolsága 5 egység?

23. Hány cm hosszú annak a téglatestnek a leghosszabb lapátlója, amelynek élei 8 cm, 12 cm és 16 cm hosszúak?

24. Hány cm hosszú annak a téglatestnek a testátlója, amelynek élei 5 cm, 8 cm és $\sqrt{80}$ cm hosszúak?

25. A $DEF$ derékszögű háromszög $DE$ befogója 7 cm-rel rövidebb, mint a $DF$ befogó. Az átfogó 2 cm-rel hosszabb, mint a $DF$ befogó. Számítsd ki a DEF háromszög kerületét!

Add össze a fenti végeredményeket (az aláhúzott kérdésekre adott válaszokat)! Az eredményhez adj hozzá még 2-t!

Oszd el az így kapott számmal a $30\,481\,879$ -et!

Az így megkapott négyjegyű szám a titkos kód. Sikerült? Életben maradtunk? Yuppi!!! ☺

Irodalomjegyzék

[1] Csahóczi Erzsébet–Csatár Katalin–Kovács Csongorné–Morvai Éva–Széplaki Györgyné–Szeredi Éva: Matematika tankönyv 5–8. évfolyam, Apáczai Kiadó, Celldömölk, 2009.

[2] Gedeon Veronika–Paróczai Eszter–Számadó László–Tamás Beáta–dr. Wintsche Gergely: OFI Kísérleti tankönyv, 7–8. évfolyam, Alföldi Nyomda Zrt., Debrecen

[3] Csordás Mihály–Konfár László–Kothencz Jánosné–Kozmáné Jakab Ágnes–Pintér Klára–Vinczéné Winter Andrea: Sokszínű matematika, 5-8. évfolyam, Mozaik Kiadó, Szeged, 2011.

[4] Urbán János–Reiman István: A Kalmár verseny feladatai, 2006-2012., A természettudományi Közlöny 2014. I. különszáma

[5] Zrínyi feladatok, 2005–2017., Mategye Alapítvány, Kecskemét

[6] Gerőcs László–Orosz Gyula–Paróczay József–Szászné Simon Judit: Matematika Gyakorló és érettségire felkészítő feladatgyűjtemény, Nemzeti Tankönyvkiadó, Budapest, 2005.

[7] Juhász István–Orosz Gyula–Paróczay József–Szászné Simon Judit: Matematika 10., Az érthető matematika, Nemzeti Tankönyvkiadó, Budapest, 2010.

[8] Róka Sándor: Szakköri kalauz, 5–6. évfolyam, Zalamat Alapítvány, Nagykanizsa, 2014.

Paróczay Eszter
Gödöllői Premontrei Iskolaközpont

Információk

Főmenü