Első tapasztalataim a kooperatív technikák alkalmazásairól az egyetemi matematikaoktatásban

Tapasztalataim szerint a matematika gyakorlatok többsége frontálisan folyik. Ez főleg akkor hasznos, ha rövid idő alatt sok ismeretet kell átadni. Szerencsére munkahelyemen, a Szent István Egyetemen a mostani félévtől eggyel nőtt a gyakorlatok heti óraszáma. Így most több idő áll a tanárok rendelkezésére, hogy ne csak elmondják, mit kell megtanulni, hanem lehetőségük nyílik arra is, hogy az órán új módszerek alkalmazásával jobban elmélyítsék a tanultakat.

Ebben például a kooperatív technikák alkalmazása segíthet bennünket. Milyen többlet várható, ha kooperatív módszereket alkalmazunk tanítási órán? Nem csak a kooperatív tanulást népszerűsítő irodalom támogatja ezt a módszert a hagyományos frontális óravezetéshez képest, hanem tanuláspszichológiai kísérletek is alátámasztják ([1], [2], [3], [4], [5]), hogy a kooperatív technikák alkalmazása során a hallgató

nagyobb érdeklődéssel áll a feladat megoldásához,
oldottabbnak, nyugodtabbnak érzi az óra légkörét,
ötleteit jobban szabadjára engedi,
kevésbé fél attól, hogy hibázik,
javul a társaival való kapcsolata.

A fejlesztő és gyógypedagógiában, alsó tagozaton, egyes tantárgyakban (például a nyelvoktatásban) magasabb évfolyamokon is régóta része a módszertani megoldásoknak a kooperatív tanulás. Napjainkban az olyan individuálisnak tartott tantárgy, mint a matematika tankönyveiben is megjelennek csoportmunkában, együttműködéssel megoldandó feladatok. A tanárképzés módszertani tananyagában jelen van ugyan a kooperatív módszer, de a matematika szakos tanárjelöltek az egyetemen saját ismereteiket alapvetően hagyományos módszerrel szerzik.¹

2017. őszi félévében a Szent István Egyetem Gépészkarán az elsőévesek matematika gyakorlatain kipróbáltam néhány kooperatív módszert. Az itt szerzett első tapasztalataimat szeretném megosztani négy, különböző típusú kooperatív tevékenységről, amelyek esetleg más néven, várhatóan ismerősek az olvasó számára.

1. Körforgás

CÉL:

Ismerkedés, közös érdeklődés, a hallgatók egymás közötti kapcsolódási pontjainak megtalálása, hogy mindjárt az első órán beszéljenek egymással, ne idegenekként menjenek haza.

LEBONYOLÍTÁS:

Egy körben egymással szemben álló párok azt a feladatot kapják, hogy egy adott jelre egy adott témáról kezdjenek egymással beszélni nagyjából két percig és találjanak mindkettőjüket érdeklő közös pontokat.
A következő jelzéskor a külső körben állók az óramutató járásával megegyező irányban a következő hallgatóhoz lépnek és a megadott új témáról kezdenek beszélgetni.

TECHNIKAI MEGVALÓSÍTÁS:

A Matematika I. tantárgy első órájának az utolsó 20 percében játszottuk.
A tábla előtt a belső körbe a kollégistákat állítottam, mert ők már ismerték egymást. A többiek velük szemben álltak. Mivel páratlanul voltak, én is beálltam.
Az általam megadott témák: zene; sport; film; szabadidős tevékenység; étel; mire használod a számítógépet voltak.
Az óra végén érdemes játszani. Ha előbb elfogynak a témák, nyugodtan lehet őket elölről kezdeni, hiszen újak a beszélgető partnerek.

EREDMÉNYEK:

Jó hangulatban zajlottak a beszélgetések, én is nagyon élveztem.
Az egy-egy témára szánt 2–3 perc elegendő volt ahhoz, hogy kapcsolódási pontokat találjanak a párok.
A 20 perc elég volt ahhoz, hogy a csoportban a párbeszédek elinduljanak, ugyanakkor nem vált unalmassá a játék.
Számomra meglepő információ volt, hogy a velem egy párba került hallgatók milyen nyíltan és természetesen kezdtek beszélgetni velem.

TOVÁBBI LEHETŐSÉGEK:

Más, esetleg a tárgyhoz kötődő témákat is lehet választani.

2. Egymást tanítjuk „villámrandi” módszerrel

CÉL:

A hallgató ne csak tanári magyarázat segítségével, hanem leírás, illetve a társa magyarázata alapján is megértse egy feladat megoldását. Másrészt ezt el is kell tudnia magyaráznia társának.

LEBONYOLÍTÁS:

A hallgatókat párokba osztjuk, akik egymással szembe ülnek le. A párokat sorba ültetjük, ami egy nagy kört formál.
Mindenki elolvassa a saját feladatát és annak részletezett megoldását. Ha nem érti, jelentkezik és segítek neki. (10 perc)
A párjának megmutatja a feladatát és elmagyarázza neki a megoldás menetét. (5 perc)
Szerepet cserélnek: a párja magyarázza el neki a saját feladatának megoldását. (5 perc)
Mindenki feladatot cserél (leírással együtt) a párjával.
A belső körben ülők eggyel odébb ülnek és az új partnerrel megismétlik a 3., 4. és 5. lépést. Gondolkodási idő már nincs. A hallgató nem leírás, hanem a társa magyarázata alapján érti meg a feladatmegoldását. (5 perc fejenként a magyarázat)
Ciklikusan ismétlődik a 6. lépés szerint a tanítási folyamat mindaddig, amíg mindenki elolvassa vagy meghallgatja az összes feladat megoldását.

TECHNIKAI MEGVALÓSÍTÁS:

Az exponenciális sorozatok végtelenben vett határértékének meghatározásánál próbáltam ki a módszert. Az előző órán a polinom és algebrai tört alakú sorozatok végtelenben vett határértékének meghatározására oldottunk meg feladatokat. Az óra elején a $q^{n}$ sorozat végtelenben vett határértékét ismételtük át.

A 20 hallgatót négyesével ültettem le. Minden blokkban ugyanúgy, az ülésrendnek megfelelően osztottam ki a kidolgozott példákat:

B	D
A	C

A magyarázta B-nek és C magyarázta D-nek a saját példáját. Majd cseréltek, és B magyarázott A-nak, illetve D magyarázott C-nek.
Ezután A és B, illetve C és D példát cseréltek.
A és C helyet cseréltek. Újra magyaráztak, majd példát cseréltek.
A és C újra helyet cseréltek és magyaráztak. Ekkorra mindenki mind a négy feladat megoldását elolvasta vagy meghallgatta.

EREDMÉNYEK:

Szerencsére néggyel osztható volt a létszám. Ha csak egy hiányzott volna, beültem volna negyediknek; ha pedig több, akkor a legjobbakat beosztottam volna a csoportokhoz mentornak.

A hallgatók maguktól leírták a füzetükbe a feladatokat és azok megoldását, mivel nyilvánvaló volt, hogy a kidolgozott példákat vissza fogom kérni.

A példákat csatolom mellékletként.

3. Rakjuk sorba!

CÉL:

Szabályok alkalmazási sorrendjének megállapítása. Egy többlépéses feladatmegoldás során általában nem cserélhető fel a lépések sorrendje. A sorrendet meg kell tanulni és végre kell hajtani. Ha a hallgató új megfogalmazásban találkozik a problémával, ellenőrizhető, hogy érti-e, tudja-e hogyan következnek egymás után a lépések. A sikeres feladatmegoldáshoz nem feltétlenül szükséges, hogy szabatosan megfogalmazza a lépéseket, de a megoldás logikájának megértéséhez pontos megfogalmazásban fel kell ismernie azokat.

LEBONYOLÍTÁS:

A feladattípus megoldásához szükséges lépéseket tartalmazó papírcsíkokat összekeverve kiosztottam a pároknak. Felhívtam a figyelmüket arra, hogy sorba rakáskor egymás mellé tegyék azokat a papírokat, amelyeken ugyanaz áll más szavakkal kifejezve.

TECHNIKAI MEGVALÓSÍTÁS:

A függvényvizsgálat I. (az első derivált segítségével az eredeti függvény menetének és helyi szélsőérték-helyeinek meghatározása) és a függvényvizsgálat II. (a második derivált segítségével az eredeti függvény alakjának és inflexiós pontjainak meghatározása) témakörben próbáltam ki az egyik óra elején. Az előző órákon már több feladatot végigszámoltunk. A cikk végén mellékletként csatolom a két lépéssorozatot.

EREDMÉNYEK:

Számomra meglepő volt, mennyire gyengén sikerült a feladat megoldása. A legtöbb pár feladta, belefáradtak, mielőtt megoldották volna a feladatot. Ez azt jelenti, hogy vagy nem tudják még több megoldott feladat után sem a szükséges lépések sorrendjét vagy nem értik a pontosan fogalmazott mondatokat. Ez mindenképp arra utal, hogy nem fognak tudni sikeresen megoldani ilyen típusú feladatokat, hiszen még ez után jönne a neheze, a lépéseket a szükséges sorrendben végre is kell hajtani.

A hallgatók párosával beszélgettek. Bár a papírdarabkák tologatása nem nagy fizikai aktivitás, mégis más típusú feladat, mint önállóan csöndben megoldani egy konkrét feladatot a füzetben tollal.

4. Készíts feladatot

CÉL:

A hallgatók nem a tanár által kitűzött feladatokat oldják meg, hanem önállóan készítenek egy saját feladatot, mely az előírt feladattípusnak megfelel. Megoldják a társuk által készített feladatot is és szükség esetén megbeszélik vele, ha a feladat típusa vagy megoldása szerintük hibás.

LEBONYOLÍTÁS:

A hallgatókat annyi csoportba osztjuk, ahány feladattípust gyakoroltatni akarunk.
Minden csoportnak megadunk egy témát, feladattípust.
A csoport minden tagja önállóan elkészít egy feladatot.
Azután a papír másik oldalán megoldja.
Annyiszor adják tovább a papírt, ahányan a csoportban vannak.
A végén mindenki visszakapja a saját feladatát.
Ezután a tanár még az órán ellenőrzi, hogy jók-e a megoldások.

TECHNIKAI MEGVALÓSÍTÁS:

A határozatlan integrál témakörben próbáltam ki.

A tanulókat hármasával ültettem egy-egy sorba. Az eredeti ülésrenden csak annyit kellett változtatnom, hogy a legjobb hármat, akik egymás mellett ültek, beültettem harmadiknak egy-egy sorba. Éppen 18-an voltak. Ha csak egy hiányzott volna, beültem volna harmadiknak.
Minden sorban az ablakhoz legközelebb ülő lett az A csoportos, a középső a B és az ajtó felőli a C. Egy játékkártya méretű papíron dolgoztak, a bal felső sarokba felírták a „Feladat” szót és a csoport jelét (A vagy B vagy C).
Az A csoportosoknak egy saját feladatot kellett írniuk alapintegrálra, a B csoportosaknak a „nulladik szabályra” (elvégzem a szorzás, osztás, hatványozás műveletet, ha lehet, hátha utána már tudom integrálni), a C csoportosaknak 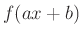$f(ax+b)$ típusú függvény határozatlan integráljára. Használhatták a füzeteiket, csak nem írhattak olyat, amit már megoldottunk.
A másik oldalra átmásolták a feladatukat és megoldották. Visszafordították a „Feladat” oldalra és a saját sorukban továbbadták. Az A csoportosok a B csoportosoknak, a B csoportosok a C csoportosoknak, a C csoportosok az A csoportosoknak.
Mindenki megoldotta a kapott feladatot a füzetében. Majd megfordította a papírt és egyeztette az ottani megoldással. Ha nem értett vele egyet, megbeszélte a feladatot annak készítőjével (és egyben megoldójával). Szükség esetén kijavították a papíron levő eredeti megoldást.
Ismét továbbadták, megismételték az előző lépést. Végül visszajutott a készítőhöz. Ráírattam a „Feladat” oldalra a nevüket és csoportonként összeszedtem. Ez eddig 25 percet vett igénybe.
Kijavítottam az összes feladatot, ők közben feladatokat oldottak meg. Visszaadtam a kijavított feladatot a készítőjének. Majd felhívtam a figyelmet minden rossz feladatra, illetve ismertettem a rosszul megoldott feladatok helyes megoldását.

EREDMÉNYEK:

Érdekes volt számomra, hogy a feladat vége után sem ültek vissza a helyükre, ott maradtak egész órán.
Kevés olyan hiba volt, hogy valaki más típusú feladatot írt, mint amit kértem az adott csoporttól. Valószínűleg azért is, mert használhatták a füzetüket. Voltak integrálási hibák is. Mindenképpen szükséges volt kijavítanom.
A feladataik nehézségi szintje tökéletesen megegyezett az órai mintapéldák szintjével. A teljes időszükséglet 40 perc volt.

Összegzés:

Szerencsére az egyetemünkre járó hallgatók fegyelmezettek, órán figyelnek, nem beszélgetnek, nem zavarják a tanítási órát. Minden tőlük telhetőt megtesznek, hogy minél többet megértsenek az ott elhangzottakból. Nemcsak a tanárral udvariasok, hanem egymással is. Nincsenek közöttük nagy szociális különbségek. Viszont igaz, hogy a felsőbb éves nem első tárgyfelvételesek kilógnak az elsőéves csoportokból. E néhány kooperatív technika első kipróbálásakor nem mértem, hogy ezáltal nőtt-e a hallgatók matematikatudása, de az órákat mindenképp színesítette, és a hallgatók közötti szociális kapcsolatokat is erősítette.

Mellékletek:

1. Melléklet. A Villámrandi négy csoportjának feladatai:

A: $\lim\limits_{n\to\infty} b_{n}=?$ , ha $b_{n}=\frac{9^{\frac{n-1}{2}}}{{(-2)}^{n+1}}$

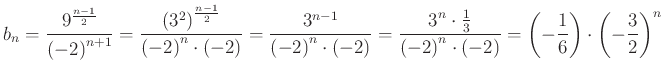
$\displaystyle b_{n}=\frac{9^{\frac{n-1}{2}}}{{(-2)}^{n+1}}=\frac{({3^{2})}^{\fr... ...{n}\cdot (-2)}=\left( -\frac{1}{6} \right)\cdot\left( -\frac{3}{2} \right)^{n}$

divergens.

A többi feladat megoldása hasonló részletezettségű volt.

B: $\lim\limits_{n\to\infty} d_{n}=?$ , ha $d_{n}=5\cdot 2^{n}-3^{n+1}$

C: $\lim\limits_{n\to\infty} c_{n}=?$ , ha $c_{n}=\frac{2^{5n+1}}{3^{3n}}$

D: $\lim\limits_{n\to\infty} a_{n}=?$ , ha $a_{n}=\frac{3^{n+1}+4^{n}}{5^{n}-2^{n+2}}$

2. Melléklet: A Rakjuk sorba! feladat lépéssorozatai

Függvényvizsgálat I. Rendezze sorba a lépéseket!

Az első derivált segítségével megállapítom az eredeti függvény menetét.

Az első derivált segítségével megkeresem az eredeti függvény helyi szélsőérték helyeit.

Deriválom a függvényt.

Megkeresem a deriváltfüggvény zérushelyeit.

Megoldom a derivált egyenlő nulla egyenletet.

Táblázatot rajzolok. A táblázat első sorába azon argumentumokat írom, ahol az eredeti függvény nincs értelmezve, illetve ahol az első derivált nulla.

A táblázat második sorába az elsőderivált-függvényt írom. Először azt, ahol nincs értelmezve, illetve ahol nulla. A többi tartományt $+$ / $-$ előjelekkel töltöm ki.

A táblázat harmadik sorában jelzem az eredeti függvény menetét. Ahol az első derivált negatív, ott az eredeti függvény csökken; ahol az első derivált pozitív, ott az eredeti függvény nő.

Ahol a derivált előjelet vált, ott az eredeti függvénynek helyi/lokális szélsőértékhelye van. A függvény menetéből látszik, hogy ez helyi minimum vagy maximum.

Ahol a derivált nem vált előjelet, ott az eredeti függvénynek nincs helyi/lokális szélsőértéke.

Függvényvizsgálat II. Rendezze sorba a lépéseket!

A második derivált segítségével megállapítom az eredeti függvény alakját.

A második derivált segítségével megkeresem az eredeti függvény inflexiós pontjait.

Kétszer deriválom a függvényt.

Megkeresem a második derivált függvény zérushelyeit.

Megoldom a második derivált egyenlő nulla egyenletet.

Táblázatot rajzolok. A táblázat első sorába azon argumentumokat írom, ahol az eredeti függvény nincs értelmezve, illetve ahol a második derivált nulla.

A táblázat második sorába a másodikderivált-függvényt írom. Először azt, ahol nincs értelmezve, illetve ahol nulla. A többi tartományt $+$ / $-$ előjelekkel töltöm ki.

A táblázat harmadik sorában jelzem az eredeti függvény alakját. Ahol a második derivált negatív, ott az eredeti függvény konkáv (szomorú); ahol a második derivált pozitív, ott az eredeti függvény konvex (mosolygós).

Ahol a második derivált előjelet vált, ott az eredeti függvénynek inflexiós pontja van.

Ahol a második derivált nem vált előjelet, ott az eredeti függvénynek nincs inflexiós pontja.

Dékány Éva

Szent István Egyetem Gépészmérnöki Kar

Irodalomjegyzék

[1] Dörner, D. (1999). Bauplan für eine Seele. Reinbek: RowohltFredrickson, B. L. (1998). What good are positive emotions? Review of General Psychology, 2, 300–319.

[2] Fredrickson, B. L. & Branigan, Ch. (2005). Positive emotions broaden the scope of attention and thought-action repertoires. Cognition and Emotion, 19 (3), 313–332.

[3] Herber, H.-J. & Vásárhelyi, É. (2005). Empirische Forschung in der Didaktik der Mathematik und ihre wissenschaftliche Dokumentation. In Parisot, K. J. & Vásárhelyi, É. (2005). Positionen – Mathematikdidaktik in Entwicklung, Salzburg: Abacus Verlag (in Druck).

[4] Kagan, S. (1985). Cooperative Learning. San Clemente, CA: Kagan Publishing.

[5] Kuhl, J. (2001). Motivation und Persönlichkeit. Interaktionen psychischer Systeme. Göttingen: Hogrefe.

Lábjegyzet

¹ Több évtizeddel ezelőtt is voltak olyan matematikatanárok, akik kooperatív módszereket alkalmaztak az óráikon, azonban az elmélet és annak gyakorlati megvalósítása Magyarországon igazán az ezredforduló után terjedt el.

Dr. Spencer Kagan: Kooperatív tanulás című alapművét az Önkonet Kft. adta ki 2001-ben, az eredetileg 1992-ben, majd 1994-ben Kaliforniában megjelent könyv szerkesztett változataként.

2004-ben indult el az akkori suliNova – Educatio kompetenciafejlesztő programcsomagok megalkotása és kísérleti bevezetése Magyarországon (itt olvasható a kooperatív tanulásszervezés módszertani segédlete), majd 2008-ban adta ki a miniszter a kompetencia alapú oktatási programok kerettanterveit. Matematikából egy egységes, 1-12. évfolyamot felölelő kerettanterv készült.

Ebből és a kapcsolódó tanártovábbképzéseken tanultakból ismerkedhettek meg az innovatív tanítók és matematikatanárok talán a legkorábban a kooperatív tanulás elméletével és gyakorlatával.

A kerettanterv a magyar matematikai nevelés jó hagyományait, értékeit megőrizve különböző területeken fogalmazott meg kiemelten hangsúlyos feladatokat, ezek egyike, ami a módszertani megújulásra vonatkozik:

„A kerettanterv új szemléletét megerősítő tevékenységi formák, módszertani ajánlások megjelenítése (pl.: páros és csoportmunka, kooperatív tanulási eljárások megismertetése).

Fontos, hogy a tanulók képessé váljanak a pontos, kitartó, fegyelmezett munkára, törekedjenek az önellenőrzésre, legyenek képesek a várható eredmények becslésére. Törekedni kell a tanulók pozitív motiváltságának biztosítására, önállóságuk fejlesztésére, ugyanakkor képesek legyenek a problémák közös megoldására is. Ennek érdekében szoktassuk a tanulókat a kooperatív munkaformához, az erre alkalmas tananyagok egyes részleteinek csoportmunkában való feldolgozásával, a feladatmegoldások megbeszélésével. A csoportmunkában elvégzett feladatok értelmezése és bemutatása közben a tanulók kommunikációs képessége is fejlődik. Differenciált munkaformákkal biztosítsuk a tehetséggondozást, és az elmaradók felzárkóztatását. Fokozatosan alakítsuk ki a matematika szaknyelvének pontos használatát és jelölésrendszerének alkalmazását.

Középiskolában is nagy hangsúlyt kell fektetni a szemléltetésre, a tanulók önálló tevékenykedtetésére annak ellenére, hogy az általános iskolai tanításhoz képest a deduktív módszerek is előtérbe kerülnek.”

Ezek az elvek ma is megfontolandók. Sajnos a kompetenciák fejlesztése az ez után következő időszakban inkább csak az alternatív iskolák programjaiban maradt meg valóban fő feladatnak. Nem kétséges, hogy az egyetemen is hasznos, ha változatos módszertannal történik a matematikaoktatás, bár nyilván másképpen kell bánni az általános iskolásokkal, mint az egyetemi hallgatókkal. Azonban megfelelő felkészülés után a kooperatív technikák közül sokat bármilyen életkorú tanulókkal érdemes kipróbálni. (A Szerk.)