Iskolánkban az évek során egyre több terembe szereltek fel interaktív táblát. Először csak a szaktantermek, később az osztálytermek táblái mellé kerültek Promethean típusú táblák. A legújabbakhoz már hangszóró is tartozik, és toll nélkül (ujjal) is vezérelhetők. Fokozatosan ismerked(t)ünk meg a tábla szoftverével, ez elég sok időt és kitartást igényel(t). Rendszeresen megosztjuk egymással az ötleteinket, hogy minél sokrétűbben tudjuk alkalmazni a matematikaórákon a táblában rejlő lehetőségeket.
A következőkben összegyűjtöttük az eddigi tapasztalataink alapján a tábla előnyeit és hátrányait:
| ELŐNYÖK | HÁTRÁNYOK |
| Precízebb óratervezést igényel, így az idővel is jobban bánunk. Az egyes órarészekhez időzítőt is beállíthatunk, amit a tanulók jobban elfogadnak („Letelt az idő, fejezd be a munkát!”). | Az órára való készülés ideje többszörösére nő még akkor is, ha már meglévő anyagot alakítunk át az adott tanulócsoportra. |
| Dolgozat feladatai, egyéb feladatsorok kivetíthetők, nem kell sokszorosítani. | Túl „pörgőssé” válhat az óra, így esetleg nem tudják a tanulók megfelelően követni a magyarázatot, lemaradnak a jegyzetelésben. |
| A feladatsorok kivetíthetősége differenciáltabb haladást tesz lehetővé. | A differenciált óravezetésben rejlő nehézségek. |
| A tankönyv ábrái, egyéb rajzok kivetíthetők, kiegészíthetők, a kiegészítések letörölhetők az eredeti ábra megváltoztatása nélkül. | Többször szükséges, hogy a tanuló lássa, hogyan is készül el a megfelelő, beszédes ábra (ekkor nem célszerű rögtön a kész ábrát kivetíteni). |
| Az ábrák, képek kellő méretben jeleníthetők meg. | |
| A különböző színek, vonalvastagságok könnyen változtathatók. A szép, színes ábra a gyerekekben is felkelti az igényt a színes, jól áttekinthető ábra készítésére. | Krétás táblára betűket szebben írunk. |
| Előre elkészített koordináta-rendszert használhatunk, esetleg függvénytranszformációk tanulásánál az alapfüggvény is előre berajzolható (közben ellenőrizhetjük, hogy ténylegesen sikerül-e a gyerekeknek az ábrázolás, segíthetünk a lemaradóknak). |
Technikai körülmények: - fel kell készülni arra, hogy valami nem működik megfelelően; - a számítógép cipelése, összeszerelése (kábelezés), szétszedése csökkenti a tanár óraközi szünetét. |
| Szerkesztés felvehető, lejátszható (közben a gyerekek közt járkálva segíthetünk nekik a megvalósításban). | |
| Házi feladat ellenőrzésénél, gyakorló órán feladatmegoldásoknál a helyes eredmények, a helyes gondolatmenet letakarható, majd megmutatható. | |
| Egyéb segédprogramok (GeoGebra) ill. animációk, internetes anyagok behívhatók. | |
| A diákok szívesebben jönnek a táblához, statikus állapotuk megszakad. | |
| Tréfás rajzok beillesztésével a monotonnak tűnő óramenetet „feldobhatjuk”. | |
| Elmenthető, visszanézhető, a hiányzóknak elküldhető. | |
| Kézkímélő (a krétától kiszárad a kéz), sőt színes krétát sem kell magunkkal vinnünk | |
| Nem elhanyagolható tény, hogy pedagógusminősítésben fontos szerepet játszik a digitális kompetencia. |
Néhány konkrét alkalmazás (táblarészletekkel) a teljesség igénye nélkül
1. Házi feladat megoldásának kivetítése (természetesen csak akkor, amikor a megoldásnak már probléma nélkül mennie „kellene”). Előnyök:
– Rövidebb időt igényel a házi feladatok ellenőrzése.
– A tanulók könnyebben felfedezhetik, javíthatják a hibáikat.
– Ki lehet hangsúlyozni a fontosabb lépéseket.
 |
2. Letakart megoldások (önálló munkánál gyors ellenőrzésre):
takarótáblácskák (ellenőrzésnél lehúzhatók)
 |
3. Szerkesztések:
a) Az interaktív táblára kerülnek az adatok, a vázlat és a szerkesztés menete (ez éppen egy oldalra kifér). A krétás táblán pedig a gyerekekkel együtt a táblai szerkesztőeszközökkel végezzük a konkrét szerkesztést. A diszkussziót is az interaktív táblára írjuk.
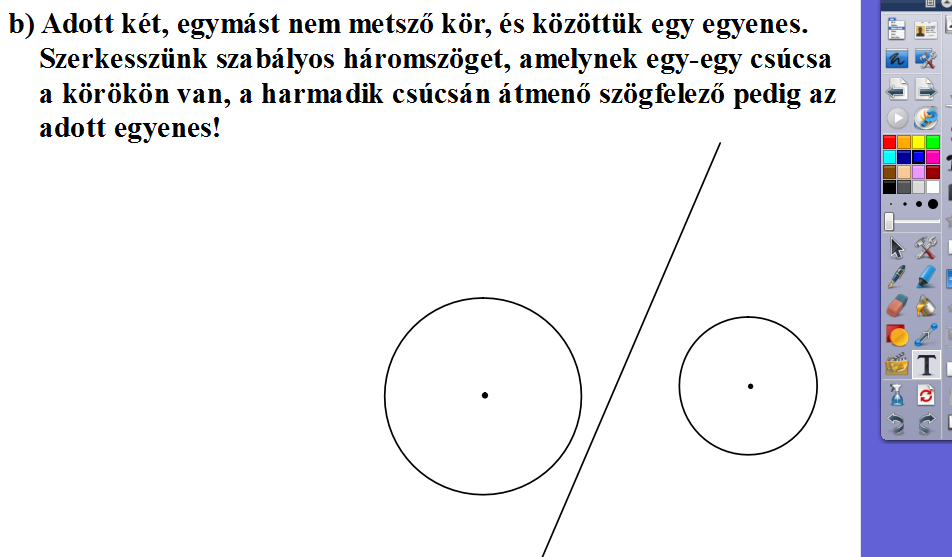 |
Megoldva elképzeljük, és megbeszéljük, lejegyezzük a szerkesztés menetét.
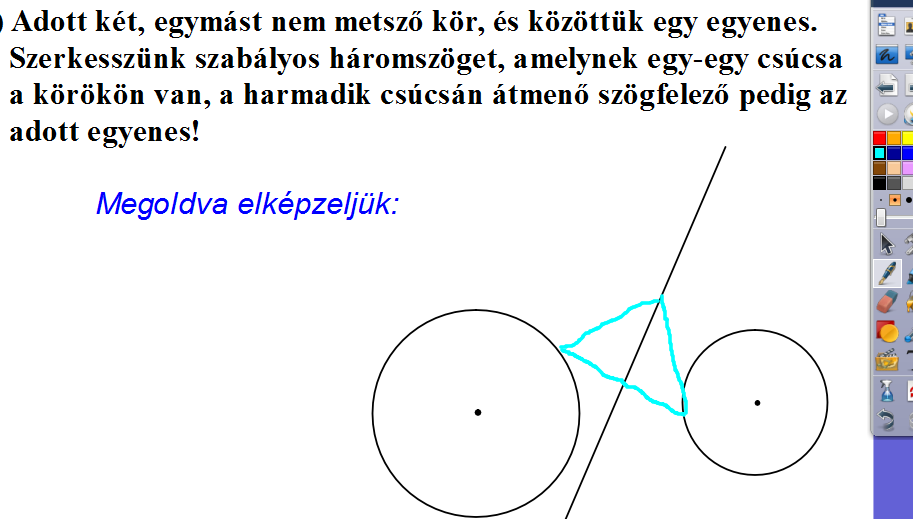 |
A következő oldalon pedig a diszkusszió következik.
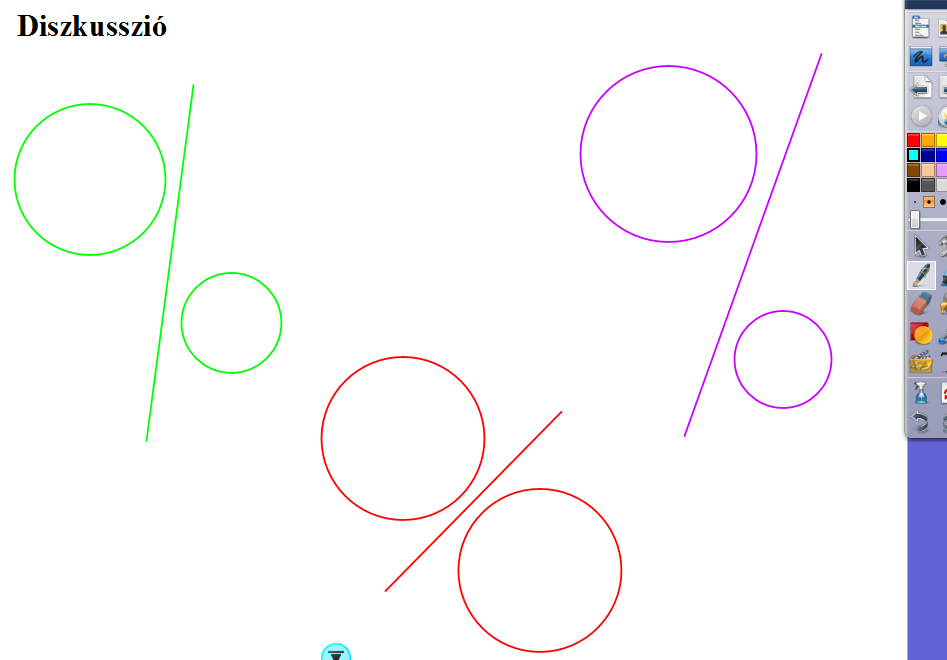 |
b) A szerkesztés rögzíthető, mint egy videó, és az órán lejátszható. Közben a gyerekeknek segíthetünk.
4. Életből vett példákhoz valódi képek beillesztése:
A gyengébb tanulók sokszor nehezen képzelik el a feladat szövegében olvasottakat. Segíthetjük őket, ha konkrét képet keresünk, amelybe színessel akár magyarázó vonalak is húzhatók. Pl:
 |
 |
 |
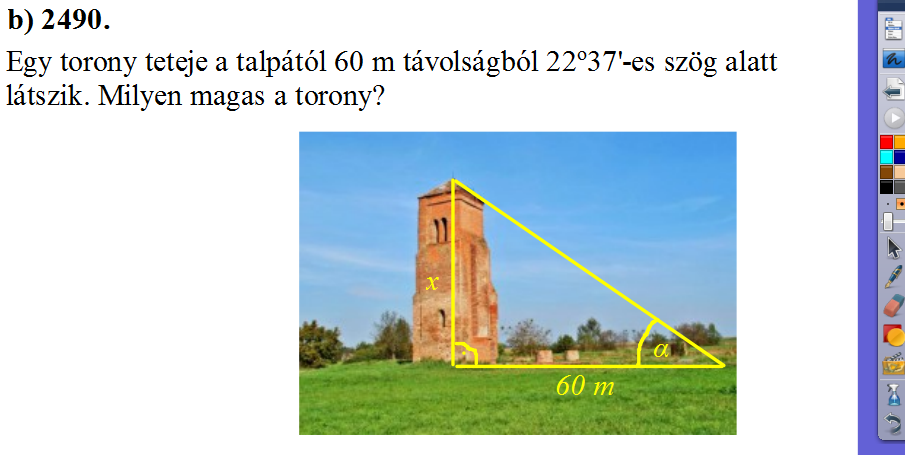 |
Pl.: ötödik osztályban a negatív számok bevezetésénél használt anyag néhány részlete:
 |
|
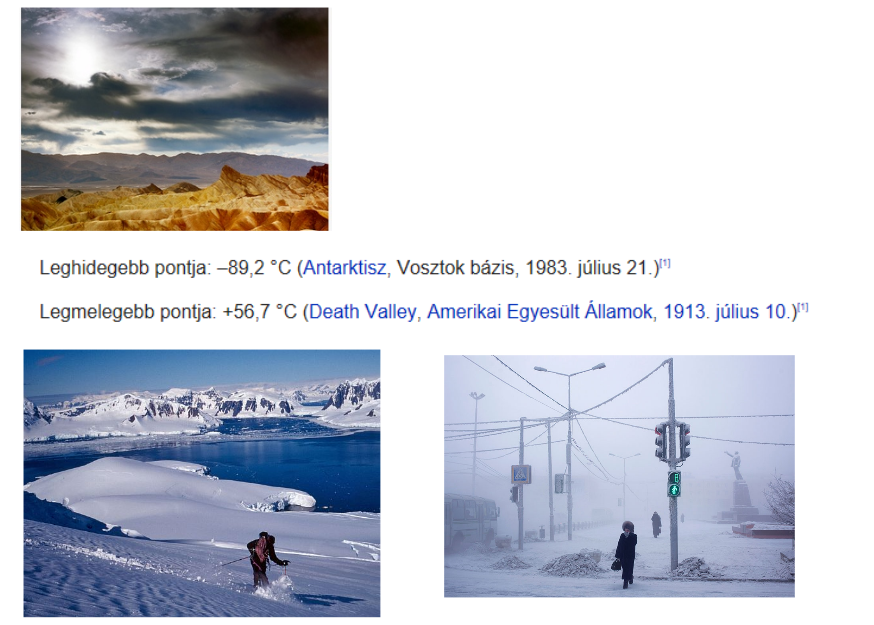 |
|
 |
Pl.: ötödik osztályban a testek szemléltetésénél használt anyag néhány részlete:
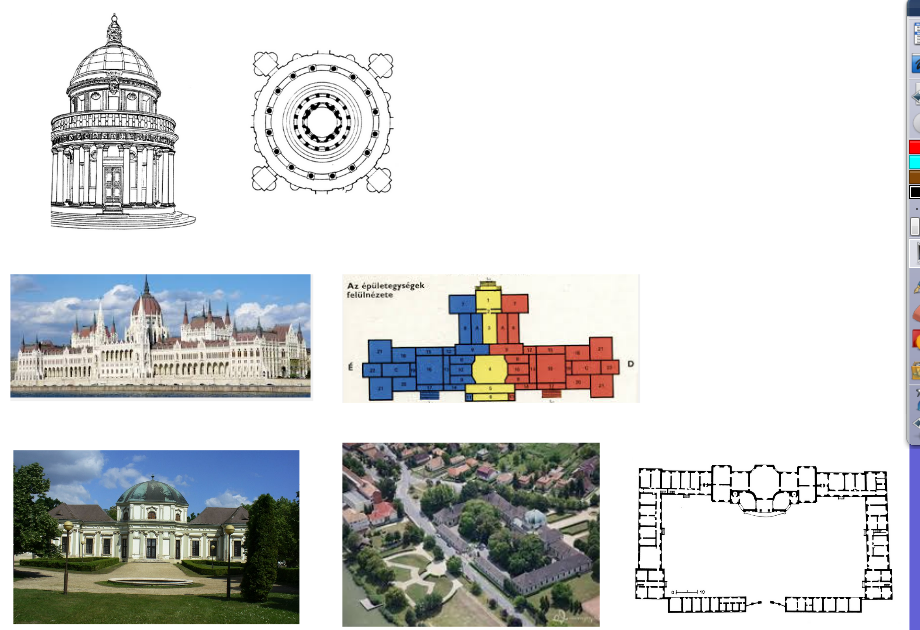 |
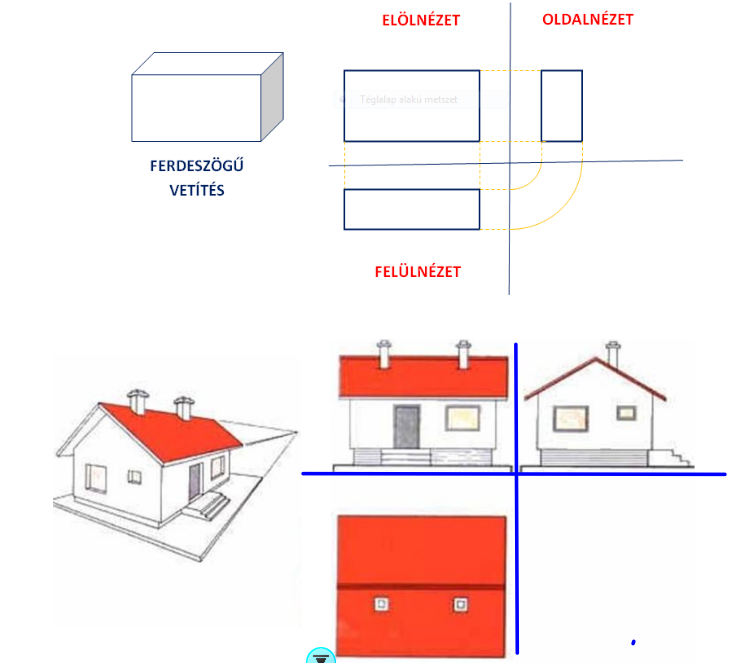 |
5. Geometriai témkörökben rendkívül hasznos a kivetíthető, módosítható, színezhető, radírozható (stb.) ábra. Pl. 8. osztályban Pitagorasz-tételhez (karácsony táján): a megoldás során a kivetített eredeti képre segédvonalakat, szögeket, kiszámolt értékeket, bármilyen adatot ráírhatunk.
Az eredeti ábra:
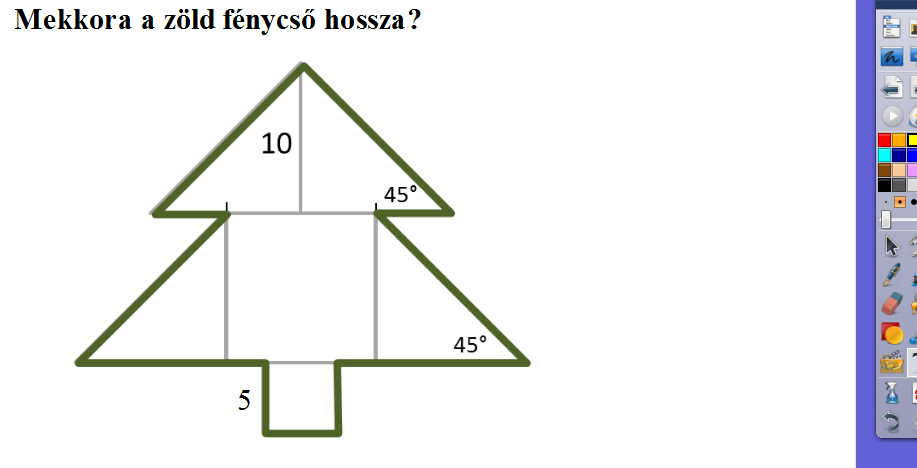 |
6. Függvények
A tanulók szívesen ábrázolnak grafikonokat az előre elkészített koordináta-rendszerben. A transzformációs lépéseket akár a grafikon mozgatásával is megmutathatjuk (merre is mozdul a görbe). A témakörbe illeszkedő házi feladatok is sokkal egyszerűbben ellenőrizhetők. Pl.: A kész ábra kivetítése után a transzformációs lépéseket a grafikonra ráírjuk, akár nyilakkal is jelölhetjük az „elmozdulásokat”, és ezzel elmélyítjük, újra átismételjük a tanultakat.
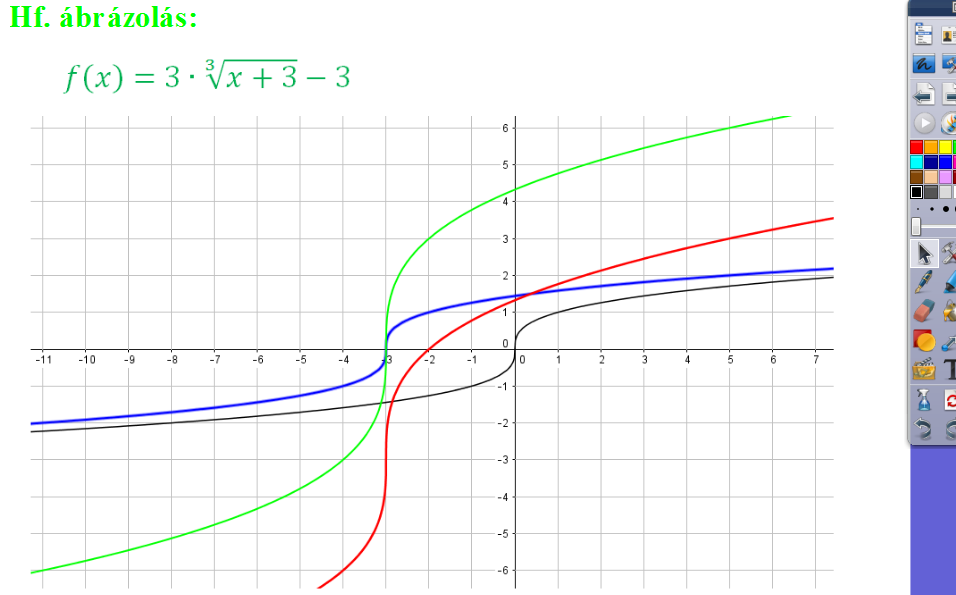 |
7. Statisztikában szinte pótolhatatlan, hogy a táblázatokat, diagramokat kivetíthetjük, amelyekbe bátran belerajzolhatunk. Ezzel rengeteg időt takarítunk meg.
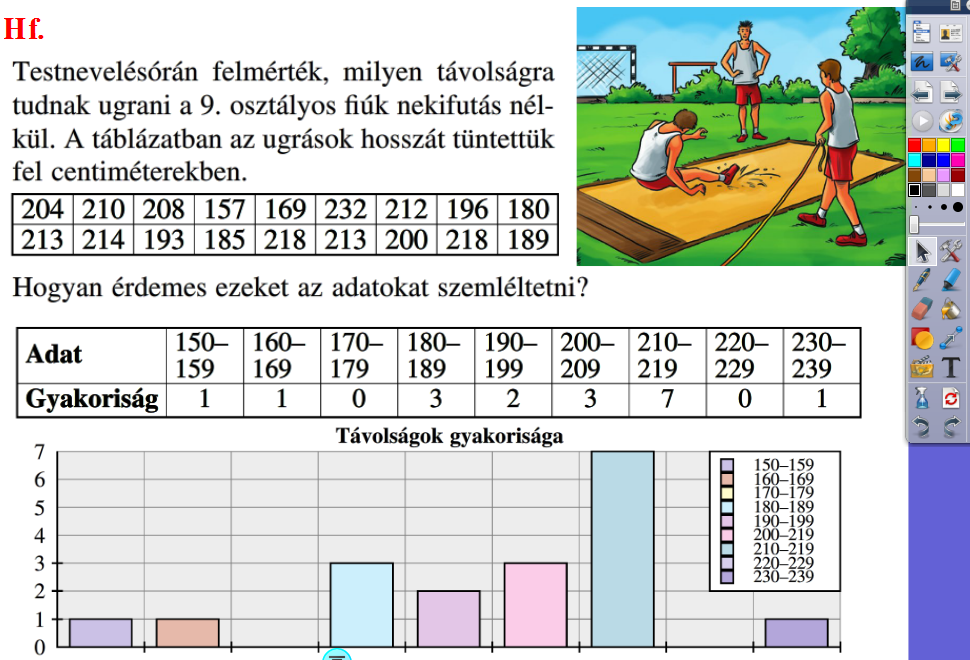 |
8. Objektumok mozgatása
a) Megfelelő sorrend felállítása „odahúzással” (bármilyen sorbarendezésnél)
 |
b) Halmazelemek elhelyezése
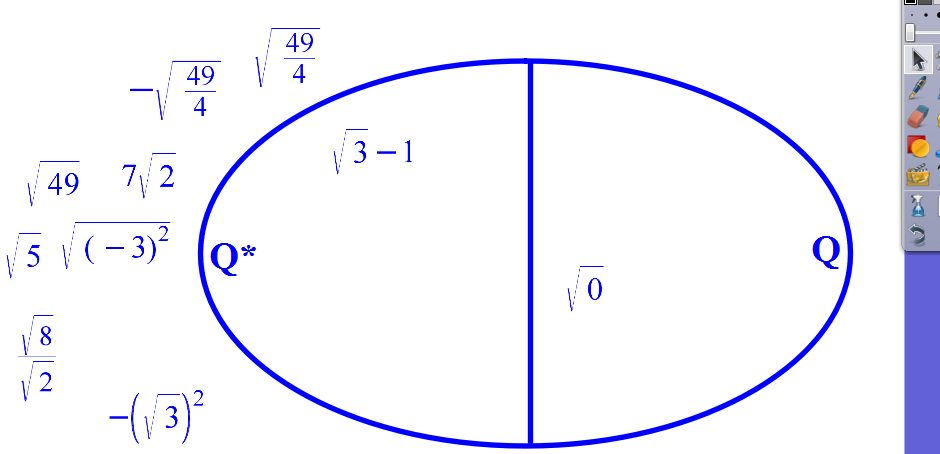 |
9. Problémamegoldás másolat mozgatásával (az eredeti objektum megmarad, de másolatot húzhatunk le róla)
a) Vektorok
Mivel a tanár által felrajzolt vektor megmarad, és vele egyenlő vektorokat „húzhatunk le” róla, ezért szinte természetes a vektorsereg és a reprezentáns fogalma. A vektorműveletek is nagyon gyorsan, szemléletesen modellezhetők, hiszen akárhová játszva elmozdíthatók a vektorok.
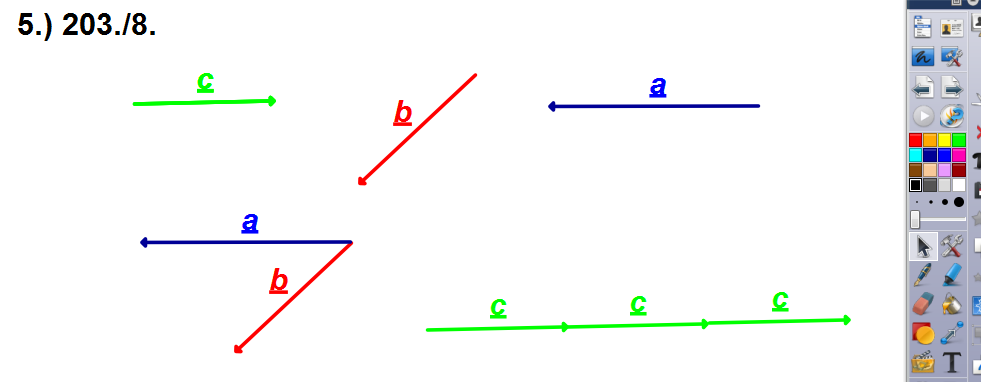 |
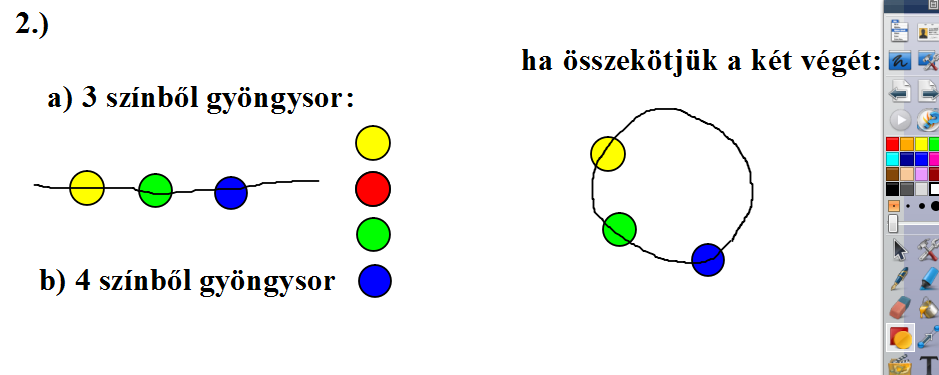
b) Kombinatorika
Még a nagyobb korosztály is szívesen próbálkozik a táblánál a különböző esetek felsorolásával. A másolatok lehuzogatásával fűzhetjük fel a láncokat, és közben meggondolhatjuk a lehetséges esetek számát, eljuthatunk az általánosításig.
 |
10. Logikai játékok megvalósítása
Pl. A közismert logikai játék változata: felváltva „röptethetjük” a lepkét úgy, hogy a legmagasabb létrafokra felérjen, de csak egy vagy két fokot repülhet felfelé egyszerre:
 |
11. „Feldobjuk az órát” (nem hátrány, ha az órának jó a hangulata is)
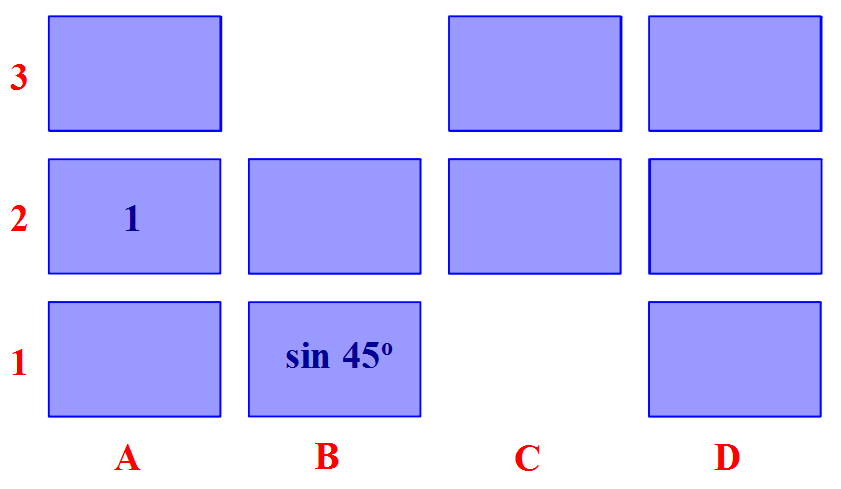
a) Memóriajáték különböző témakörökben
 |
b) Tréfás képek
 |
 |
12. Egyéb eszközök
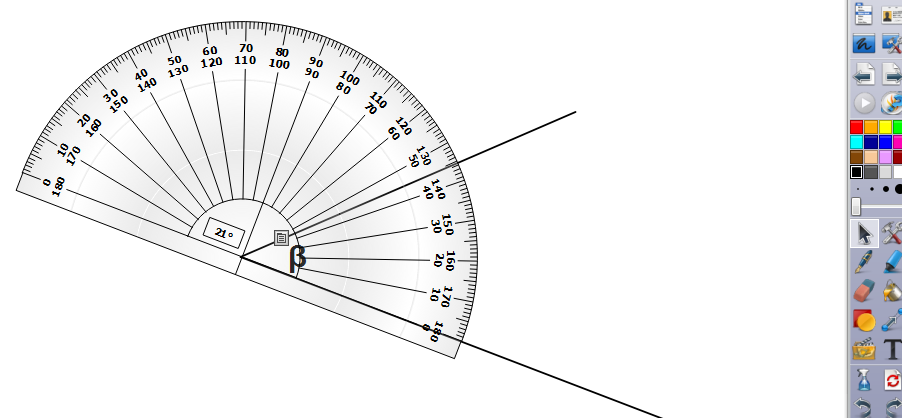
a) Szögmérő (hasonló a táblai szögmérőhöz)
 |
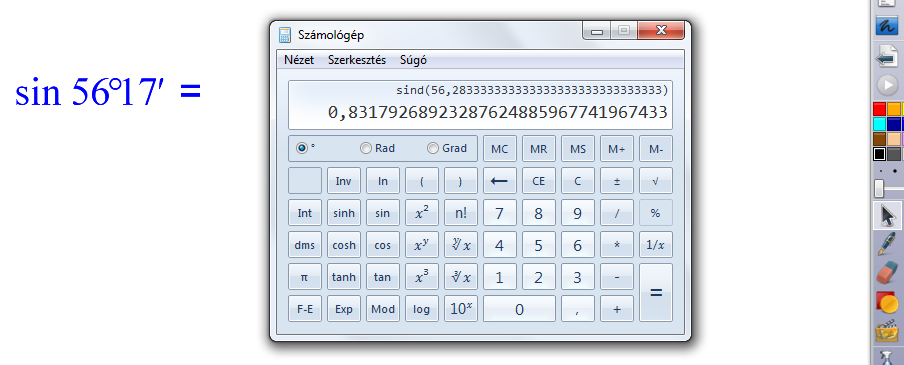
b) Számológép
Nagy segítség pl. trigonometrikus függvények alkalmazásánál. A gyerekek látják, lépésenként követik, hogy a tanár hogyan használja a számológépet. Meg lehet beszélni a különböző számológép típusok műveleti sorrendjét. A kapott értékek kerekítését is könnyen tisztázhatjuk.
 |
c) Kockagurító
Pl.: Dobjunk 6-szor egy szabályos dobókockával! Minden dobás után írjuk be a dobott értékeket a hiányos összeadásba úgy, hogy az összeg a lehető legnagyobb legyen! (Előnye: nem egymást szidják a gyerekek, hogy valaki „rosszat” dobott.)
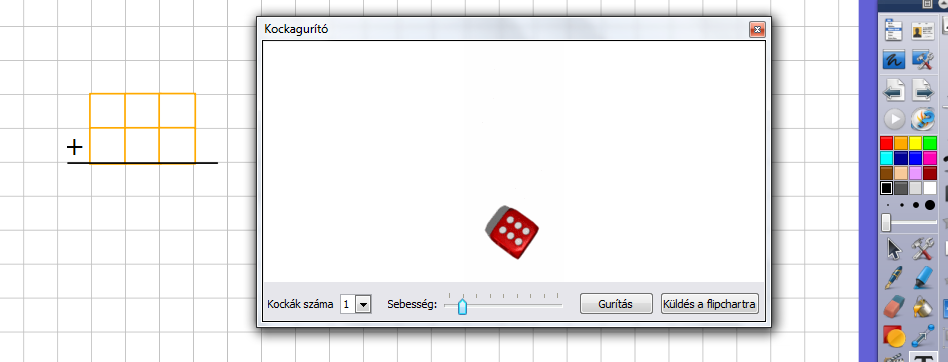 |
d) Felfedő alkalmazása (ne látszódjék a teljes táblakép, így egy feladatra tudunk koncentrálni)
A fekete rész fokozatosan le/elhúzható:
 |
Végezetül néhány vélemény diákoktól:
„Az interaktív táblának sok előnye és hátránya van. Először is több, mint egy egyszerű projektor, mivel erre az eszközre írni is lehet, anélkül, hogy a krétától kiszáradna a kezünk. Továbbá tanítás közben egy kattintással előhozható a már előre megírt feladat, ezáltal kevesebb időt vesz el az órából, mintha krétával kellene fölírni a táblára. Csakhogy a diáknak a füzetébe ugyanúgy le kell írni, másolni a feladatot, ezáltal az elvileg megtakarított idő elvész. Másik hátránya, hogy felülete a hagyományos táblákéhoz elég kicsi, így van, amikor egyszerre csak egy feladat van fönn a táblán, és ilyenkor azoknak a diákoknak, akik gyorsabban oldják meg a feladatot, várniuk kell. Továbbá kis felülete miatt egy hosszabb feladat levezetése nem látható teljes egészében. Szerintem az okostábla hasznosabb lehetne akkor, ha a tanulóknak tabletjük/laptopjuk lenne, amin az órai anyag vázlata ugyanúgy megjelenne, mint az interaktív táblán.” (Balogh Kristóf 11.oszt.)
„Szerintem az interaktív tábla színt visz a tanulásba, hiszen az összes elektromos kütyü vonzza a diákok figyelmét. Lehetőséget ad a távtanulásra (pl. ha beteg valaki, akkor egy az egyben megkapja az órai anyagot és be tudja pótolni). Lehet rajta akár videókat nézni, ami szintén jobban megmarad a fejünkben, mintha a tankönyben olvasnánk valamit. Összességében az elektronikus tábla szerintem egy szuper dolog.😊” (Kovács Mariann 11.oszt.)
„Nagy segítséget nyújt nekem az anyag elsajatításában, hogy egy képi megerősítést is kapok e táblák által, illetve szintén segíthet azoknak a gyerekeknek, akiknek nem igazán szívük csücske a matek: akár a legszárazabb feladatokat is fel lehet dobni vicces és érdekes képekkel. Élővé varázsolja a táblán megjelent tartalmat, szemléletesebbé teszi az órákat. Ha valakik lassabban jegyzetelnek a többiekhez képest, akkor kedvükért egy gombnyomással vissza lehet térni az előző oldalakhoz. Én csak jó véleménnyel tudok lenni ezen táblákról. (Rimek Adrienn 11. oszt.)
„Véleményem szerint az interaktív tábla mindenképp pozitív változás a diákok életében. Az órákra tankönyv nélkül érkezhetünk, hiszen a táblán megjelenik, így gördülékenyebben folyik az óra. Sokszor mi is használhatjuk a táblát a toll segítségével így még színesebbé teszi az órákat és sokak figyelmét felkelti. Könnyen átláthatóvá teszi a bonyolultabb ábrákat a sok szín és alakzat segítségével. Én csak előnyét látom ennek a korszerű találmánynak.” (Zsiborács Dorottya 9.oszt.)
„Én nagyon szeretek az interaktív tábláról/val tanulni, egyrészt mert sokkal gyorsabban, folyékonyabban megy az óra menete, ha a feladatok alapból ki vannak vetítve a táblára, másrészt pedig sokkal látványosabban lehet bemutatni a példákat, a változatos színeknek, mintáknak, alakzatoknak, változtatható tollvastagságnak köszönhetően. Így mi, diákok is jobban megértjük, mintha könyvből bogarásznánk ki. Szerintem egy mai fiatalt sokkal jobban leköt már alapból az okos tábla látványa, mint egy hagyományos krétás tábláé, nem beszélve arról, hogy majdnem mindenki örömmel megy ki a táblához megoldani egy feladatot, pláne ha még színt is választhat és még kréta poros sem lesz. Én hátrányt csak tanári szemszögből tudnék mondani, mégpedig azt, hogy ahhoz, hogy tényleg hasznos, érdekes legyen az óra, a tanároknak profin meg kell tanulniuk használni a táblát, és a feladatokat előtte föl kell telepíteniük, ami lehet, hogy egy kicsit idő igényes. De a tanárok lassan mindent bevetnek, hogy elérjék azt, hogy az adott tantárgyra figyeljünk és én azt mondom, hogy ez egy viszonylag nyerő módszer. 😊” (Márkus Réka 9.oszt.)
„Szerintem egy nagyszerű eszköz a tanításban az interaktív tábla. Az óra menetét nagyban meggyorsítja azzal, hogy nem kell felírni a táblára a feladat szövegét vagy rajzát krétával, hanem egyszerűen ki lehet vetíteni, így marad idő több dologra az óra keretén belül: például valamilyen témát ki tudunk bontani vagy típus példát lehet megoldani. A másik nagy előnye, hogy elmenthető és megosztható. Így a tanár el tudja küldeni a diákoknak emlékeztetőbe, és a hiányzóknak könnyebb így pótolni és tartani a tempót a többiekkel. Ha valami nem világos a füzetünkben leírtakban, akkor könnyen meg tudjuk nézni, hogy pontosan mit is írtunk és így a hibákat kiküszöbölve tudjuk megtanulni az anyagot. Szóval nagyban egyszerűsíti a tanítást mind tanár szempontból, mind a diák szempontjából.” (Dauner Domonkos 10.oszt.)
„Én szerettem a tábla használatot, mivel kényelmesebb és nem piszkol. A legnagyobb előnye ellenben az, hogy vissza lehet lapozni, míg a táblát le kell törölni, és onnantól elveszik a vázlat. A hiányzó gyerekeknek is előnyösebb.” (Necz András 10.oszt.)
Antalné Rakonczás Éva
(Budai Ciszterci Szent Imre Gimnázium matematika munkaközössége: Csombó Emese, Gálné Palágyi Erzsébet, Lőrincz Éva, Mig Balázsné, Wirnhardtné Matolcsy Erzsébet)









