Matematikusként sokszor tapasztaltam már, hogy az emberek többségének fogalma sincsen, mit jelent ezt a szakmát művelni a gyakorlatban, vagy hogy egyáltalán mi is az a matematika; pláne, hogy ezen belül topológiával foglalkozom, amiről a legtöbben még csak nem is hallottak. Pintér Gergő Új világok teremtése című könyvét – kicsit tisztességtelenül – már azelőtt is ajánlottam a munkám iránt érdeklődő ismerőseimnek olvasásra, hogy én magam akár csak belenéztem volna. Most, hogy elolvastam, már nyugodtan mondhatom, hogy jól tettem: remek ismeretterjesztő könyv, ami, bár a fülszöveg szerint laikusoknak szól, még a matematikában jártasabb embereknek is szórakoztató lehet (nekem legalábbis az volt).
A könyv egyik fontos inspirációja Péter Rózsa Játék a végtelennel című könyve; az Új világok teremtése ugyanebben a szellemben íródott, azaz képletek és precíz definíciók, számítások helyett a matematikai (és itt kifejezetten a geometriai és topológiai) szemlélet felépítése és bemutatása a cél. A könyv címe Bolyai János híres levelére utal, amelyben apjának számol be a hiperbolikus geometria megalkotásáról úgy fogalmazva, hogy „semmiből egy ujj más világot teremtettem”. Az akkor forradalmian új ötlet, az absztrakt objektumok szabad konstrukciója és ezek vizsgálata az azóta eltelt 200 évben természetes részévé – sőt, alapjává – vált a matematikának, amiről viszont azok, akik nem kifejezetten matematikai képzettségűek, nem sokat tudnak. Az iskolában a matekot általában úgy tanítják, hogy egy adott(nak vélt) rendszerben dolgoznak, és nem lépnek ki belőle, hogy más szabályok szerint működő valóságokat is bemutassanak. Így a laikusok számára rejtve marad a teremtésnek ez a szabadsága és ezzel együtt a matematika alapgondolata: hogy nem a valóság közvetlen leírása a célunk, hanem annak egy-egy részét megfogó modellek megalkotása, és ezen modellek vizsgálata, ami aztán információt adhat a (lehetséges) valóság(ok)ról is. Az Új világok teremtése fő eleme pontosan ennek a gondolatnak a bemutatása olyan módon, hogy azok az érdeklődők is be tudják fogadni, akiknek semmilyen előképzettségük sincs, viszont olyan hitelesen, hogy a matematikai tartalom se torzuljon az egyes konstrukciók szemléltetése során.
A könyv alapját Pintér Gergő ismeretterjesztő előadásai, a MateMorfózis-szeánszok képezik; az egyes fejezetekben egy-egy előadás témáját dolgozta fel, illetve fejtette ki bővebben, ahogyan erről már a könyv készülése közben az Érintőben is írt. Követve a személyes ismeretterjesztés logikáját, a könyvben is sok témát párbeszédes formában mutat be. Ez a (fiktív) párbeszéd mindig Gergő (G) és egy Túlművelt Érdeklődő (T) között zajlik általában olyan módon, hogy a felvetett témával vagy problémával kapcsolatban T kérdéseket tesz fel, ezekre G válaszol, rávezető ötleteket ad, és ezen folyamat során során közösen jutnak el a megoldásig. Itt a „túlművelt” jelző arra utal, hogy az érdeklődő már rendelkezhet egyfajta ismerettel az adott témáról, akár az iskolai tanulmányaiból, akár valahonnan máshonnan, viszont sokszor épp egy berögzült világkép akadályozza meg az embert a fogalmak szabad újraértelmezésében. Éppen ezért a könyv lebontja a már ismerős fogalmakat, hogy aztán egy tágasabb világ apró részeként tudja őket újraértelmezni, illetve ezen keresztül tud bemutatni egy sereg új konstrukciót. Az így teremtett új világok túlnyomórészt a geometria és a topológia objektumai, így sok helyen elengedhetetlenek a szemlélet megértéséhez a képes illusztrációk. Szerencsére az Új világok teremtése bővelkedik ezekben, a könyvet illusztráló – egyébként szintén matematikus – Szabari Mátyás rajzaival majd minden lapon találkozhatunk és ezek nagyon sokat hozzátesznek az érthetőséghez. Szerepelnek ezen kívül a témához kapcsolódó dalszövegbetétek is a könyvben, ezek nagyrészt Pintér Gergő (valamelyik zenekarának) dalai, de más magyar könnyűzenei előadók dalait is megtalálhatjuk itt.
Rögtön az első fejezet egy olyan fogalommal, a dimenzióval foglalkozik, amiről sokaknak van már kialakult képük: a minket körülvevő háromdimenziós tér és esetleg az idő, mint negyedik dimenzió. Itt tehát a feladat ezt a képet lebontani, megtalálni a fizikai fogalom matematikai gyökereit, majd ezen keresztül újraértelmezni azt; a fejezet így szemléletet ad az olvasónak magasabb – akár végtelen – dimenziós terekről, illetve megismertet új fogalmakkal is, amikre gondolhatunk egyfajta dimenzióként.
A második fejezet vezet át a topológia világába, ezen belül pedig (kimondatlanul) az absztrakt sokaságok elméletébe. Azzal a viszonylag népszerű kérdéssel kezd, hogy hogyan is nézhet ki a világegyetem „nagyban”, amit aztán pontosít arra, hogy a tér alakját szeretnénk vizsgálni, csakhogy ehhez tudni kell az alakot a tér belső tulajdonságaként értelmezni. Ennek a problémának a kibogozásához kétdimenziós konkrét terek (tórusz, gömb, Klein-kancsó) példáján keresztül visz minket a könyv, aminek során eljutunk az irányíthatóság fogalmához, a topológiai ragasztásokhoz és – bizonyítás nélkül – az irányítható zárt felületek osztályozásához.
A harmadik fejezetben aztán látszólag egész más vizekre evezünk, és megtanulunk Dobble-féle kártyapaklit gyártani. A gyerekek (és szüleik) körében pár éve népszerű Dobble-kártyajáték a hetedrendű projektív síkon alapul olyan módon, hogy minden kártyalapon 8 ábra van és bármely két lapon pontosan egy közös, illetve ha a pakliban szereplő 55 laphoz még kettőt hozzávennénk, akkor az is igaz lenne, hogy bármely két ábrához pontosan egy olyan lap van, amin mindkettő szerepel. Ahhoz tehát, hogy megértsük a Dobble-pakli struktúráját, meg kell értenünk a projektív síkokat és a véges testeket, valamint az ezek fölötti geometriákat; ezen a folyamaton vezeti át az olvasót a fejezet.
Ezután a negyedik fejezet kapcsolja össze az előző kettőt úgy, hogy a (valós) projektív sík topológiai tulajdonságait vizsgálja. Megmutatja, hogy a projektív síkban van egy Möbius-szalag, ezen keresztül pedig – megint csak bizonyítás nélkül – megismertet a zárt felületek teljes osztályozásával. Itt is és a második fejezetben is szó esik a felületek térbeli megvalósításairól és itt lehet igazán megérteni, hogy miért volt fontos a felületek belső tulajdonságainak megértése: amíg a második fejezetben tárgyalt felületek egész jól felismerhetőek a térben, addig a projektív sík térbeli képei már nagyon keveset mondanak a valódi alakjáról. A fejezet végén – ellentétesen a MateMorfózis és a könyv vezérelvével – egy konkrét matematikai számolás szerepel: annak a bizonyítása, hogy a különböző típusú kúpszeletek (ellipszis, parabola, hiperbola) csak az affin síkon különböznek egymástól, a projektív síkon ugyanolyanok; ez egy kitekintés arra vonatkozóan, hogy matematikai jelenségeket hogy lehet absztrakt új világok teremtése segítségével megérteni, és nyugodtan kihagyható, nincs rá szükség a könyv további részében.
Az ötödik fejezet a „tökéletes öleléssel”, azaz a – négydimenziós euklideszi térben természetes módon létező – háromdimenziós gömbfelületnek két tömör tóruszra való felbontásával foglalkozik. Ehhez – részben az első fejezetben látottak alapján – felfedezzük a magasabb dimenziós terekben élő gömböket, majd több szemléltetést is látunk arra, hogy hogyan állnak a háromdimenziós gömbön az egész teret kitöltő „ölelkező” tóruszok. Az előző fejezethez hasonlóan itt is van egy kis matematikai kitekintés, ezen tóruszok egyenletét levezetve.
A hatodik fejezet talán az, ami a leginkább belemegy a topológia technikáiba. A terek lyukasságának a fogalmát igyekszik megfogni úgy, hogy ez a tér belső tulajdonsága legyen. Ehhez a korábban vizsgált felületek – a tórusz, a gömb, a Klein-kancsó és végül a projektív sík – lyukasságának leírását tűzi ki célul, és a probléma (lyukasság, mint belső tulajdonság) megfogásához szemléletesen bevezeti a fundamentális csoport fogalmát. Bár a fundamentális csoport, mint funktor a pontozott topologikus terek homotopikus ekvivalenciaosztályainak kategóriájából a csoportok kategóriájába, eléggé elvont fogalom, itt mégis nagyon is közérthető formában van leírva, sőt, alkalmazva is: ennek segítségével oldjuk meg azt a feladatot, hogy hogyan lehet egy képet egy hurokkal felakasztani a falba vert két szögre úgy, hogy ha bármelyiket kihúzzuk a szögek közül, akkor már leesik. Ide kapcsolódóan megismerteti a fejezet az olvasót a fedő terek fogalmával, amikre gondolhatunk a terek „lyuktalanításaként”, végül pedig szó esik a lyukasság más dimenziós megfelelőiről is, ezáltal pedig a fundamentális csoport más dimenziós megfelelőiről, a homotopikus csoportokról – ezek az algebrai topológia alapvető és sokat vizsgált elemei.
A hetedik fejezetben a szimmetriákat vizsgáljuk azzal a fő céllal, hogy megértsük a háromdimenziós euklideszi tér forgatásainak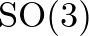 
terét. Ez persze azt jelenti, hogy egy olyan teret kell vizsgálnunk, aminek a pontjai elvont fogalmak: a tér szimmetriái. Ehhez a fejezet először tisztázza a szimmetriák fogalmát, majd – egy dimenzióval lejjebb lépve – azonosítja az euklideszi sík forgatásainak 
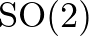terét a körvonallal; ezután – immár visszatérve az eredeti problémára – az első fejezet alapján megmutatja, hogy 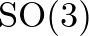háromdimenziós, majd az „öves trükkel” szemlélteti 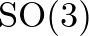fundamentális csoportját, végül pedig azonosítja 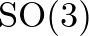-at a háromdimenziós projektív térrel, a harmadik fejezetben bevezetett projektív sík háromdimenziós megfelelőjével. Ezután foglalkozik magasabb dimenziós terekben élő szimmetrikus testekkel, végül pedig a részecskék rejtélyes tulajdonságával, a spinnel, amely fogalmat épp 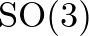segítségével lehet megfogni.
Az utolsó, nyolcadik fejezet témája az általános relativitáselmélet, pontosabban annak matematikai modellje. A fejezet két paradoxonnal indít, aztán végigvezet minket a klasszikus, newtoni fizika világképén, amiben a sebesség relatív, de az idő abszolút; majd az abszolút fényterjedésre alapozva elveti az abszolút időt és szemléletesen bemutatja a speciális relativitáselméletet, ahol a négydimenziós téridőben a múltbeli és jövőbeli fénykúpokban található a múlt és a jövő „belátható” része. Végül ebben a modellben az egyidejűség fogalmát alaposan kielemezve kapjuk a feloldását mindkét paradoxonnak.
Így tehát az Új világok teremtése tartalma hű a címéhez, a könyv során jó pár absztrakt világ teremtésén végigmegyünk, és arra is látunk rengeteg példát, hogy hogyan lehet ezeket az elsőre nagyon elvont fogalmakat mégis megérteni és használni. Azontúl, hogy a könyv több gyakorlati alkalmazást is mutat absztrakt matematikai módszerekre, szerintem a legfontosabb mondanivalója a konstrukciók szabadságában van: azt teremtünk meg, amit épp akarunk és ha ez valaminek a megmutatására alkalmas, az igazolja a teremtés létjogosultságát. Ajánlom ezt a könyvet mindenkinek, aki nem nagyon jártas a matematikában, de szeretné mégis megérteni a „térteremtés” folyamatát és a geometriai, topológiai gondolkodást, vagy aki a tanulmányai során szeretné fejleszteni a szemléletét ezekben az irányokban.
ELTE TTK, Matematikai Intézet