„Egy algebrakönyvet órákon át lapozol oda-vissza, mert próbálod megjegyezni, hogy most akkor mi mit is akar jelenteni. És ha egy bizonyítás vagy egy példa végre összeáll, általában akkor sem valamilyen konkrét kép jelenik meg a fejedben, sokkal inkább csak egy mintaszerűség. „Valami történt itt, és valami szimmetrikus dolog történt ott, csak épp fordítva.” Vagyis a kapcsolatok és a struktúrák tiszták, de aktuálisan nincsenek jelen objektumok. Ahhoz, hogy az ember az ilyen típusú algebrát művelni tudja, kell egy bizonyos tudatállapot. El kell felejtened a való világ dolgait, a fákat, a székeket, aztán el kell felejtened a matematika világát is, mert itt már nincsenek alakzatok és számok sem. Ki kell ürítened az elmédet, mintha valamilyen szigorú előírások mentén vezetett meditációra készülnél.” (A könyvből: 109. oldal)
Milo Beckman könyve a matematika lényegét igyekszik megragadni és közelebb hozni a hétköznapi olvasókhoz. A 28 éves manhattani születésű amerikai matematikus srác már egészen fiatalon megfertőződött a matematika szeretetével. 13 évesen ő vezette a New York-i Matematikacsapatot, rengeteget publikált szaklapokban, számos szervezetnek dolgozott tanácsadóként különböző matematikai jellegű problémák kapcsán. Már kisgyerekként lenyűgözték a könyvek, az olvasás és az írás. Rendkívül nyitott és kommunikatív, szenvedélyesen mesél a világ nagy összefüggéseiről, szereti a képszerű példákat.
A matematikát egy nagy faként képzeli el, amelynek a törzsét az iskolában mindenki által megtanult matematikai fogalmak alkotják. Ez három vastagabb ágban folytatódik, ezek: a topológia, az analízis és az algebra. A fa lombja a kapcsolat a mindennapi élet legkülönbözőbb területeivel a matematikai modellalkotás segítségével, amelyen a matematika alkalmazott területei által teremnek gyümölcsök. A fa gyökérzetét a történelmi előzmények és a matematika létjogosultságához kapcsolódó filozófiai kérdések adják.
.
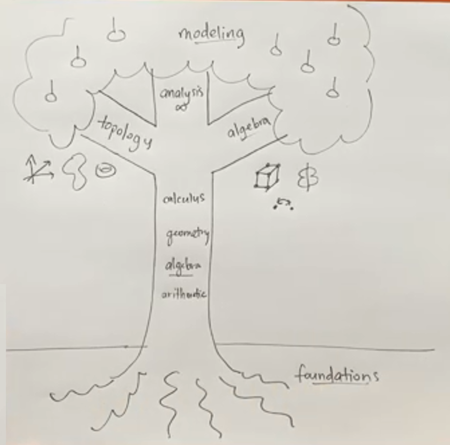
Beckman rajza a matematika felépítéséről és kontextusáról. (Forrás: https://www.youtube.com/channel/UCURP6q1VjGEFfy7GPP3Tm0w.)
A könyv célja, hogy széles körben bemutassa a matematika legmélyebb fogalmait minél egyszerűbben, szemléletesebben, ugyanakkor valamennyire átfogó képet adjon a matematika területeiről, és szoros kapcsolatáról mindennapi életünkkel, valamint a tudományos és társadalmi kontextusokkal. Igyekszik közelebb hozni az embereket ehhez a csodálatos tudományhoz. A kedves, logikusan felépített megfogalmazás egyébként le sem tagadhatná, hogy elsősorban az amerikai átlagembereket hivatott megcélozni. Gondolkodásra buzdítja az olvasót, ugyanakkor egészséges játékra invitálja, amit játékos matematikai fejtörőkkel tarkít.
Egyszerre van jelen a matematika igazi mélysége és a hétköznapi ember egyszerű nyelvezete. A felépítés keretes szerkezetű, az elméleti matematika fontos területein fejezetenként (Topológia, Analízis, Algebra) elindulva és fontos fogalmakat bemutatva áttér a történeti alapokra és a lényeges filozófiai kérdésekre. Majd mindezeknek a gyakorlati jelentőségét az alkalmazott matematika szemüvegén át is szemügyre veszi a modellalkotás lényeges kérdésein keresztül, megemlítve az automaták igen termékeny területét, hogy a természet átfogó megértésére törekvő standard modell visszavezessen az elméleti matematika nagyszerűségéhez és megkerülhetetlen szerepéhez.
A cím ígérete, miszerint − a szó szoros értelmében véve − számok nélkül barangolunk a matematika ösvényein, valóban teljesül. Azonban az a képszerűség, amit ezáltal kínálna, pont ezért több ábrát; színes, nagyobb méretű képeket kívánna meg! A felvetett témákat, bemutatott fogalmakat mindenképpen szemléletesebb lett volna szerteágazóbb képi világgal illusztrálni!
Kezdésként Beckman a leginkább megragadható, leghétköznapibb, körülöttünk lévő fogalmakkal indít, a formák, alakzatok és sokaságok kérdéskörével, és ezek osztályozásával. Sorra kerülnek a topológia kedvelt objektumai: síkidomok, gömbök, tóruszok, Möbius-szalagok, Klein-kancsó, politópok.
Gömb és különféle tóruszok. (Forrás: https://cemc.uwaterloo.ca/events/mathcircles/2019-20/Winter/Junior6_Mar03.pdf.)
Möbius-szalag és Klein-kancsó. (Forrás: http://gyerek.jakd.hu/index.php?p=evfordulo&id=1950.)
Az 5 szabályos poliéder. (Forrás: https://d138zd1ktt9iqe.cloudfront.net/media/seo_landing_files/types-of-polyhedron-2-1621858965.png.)
A dimenziók tárgyalásakor megemlít magasabb dimenziós objektumokat is.
Tesseract (négydimenziós hiperkocka). (Forrás: https://hu.m.wi https://hu.m.wikipedia.org/wiki/F%C3%A1jl:Tesseract.gif.)
Pentakoron. (Forrás: https://www.scientificlib.com/en/Mathematics/Geometry/images/UniformPolychora.png.)
A könyv lényegi célja miatt, tudniillik, hogy a laikus hétköznapi emberek is könnyen belelássanak az elméleti matematikusok munkájának gyümölcsébe, néhol szakadékot, legalábbis réseket vélünk felfedezni a pontos, egzakt tudományos fogalmak háttere és a szövegben felvázolt magyarázatok között. Ez persze nem feltétlenül von le a könyv értékéből, ha figyelembe vesszük, hogy mennyire közel hozza olvasóit a matematikához. Viszont a való életből vett példákban, amikhez kapcsolni igyekszik a bemutatott fogalmakat, néhol felfedezhetők pontatlanságok:
„Hiszen a hallásunkat egyetlen változóval, a hangmagassággal (frekvenciával) írjuk le, és mégis az emberek nap mint nap hoznak létre olyan új alkotásokat, amelyek a többitől különböző módon vezetnek végig bennünket röpke néhány perc alatt ezen az egydimenziós téren.” (49. oldal)
Azért az emberi hallás ilyen figyelemreméltó leegyszerűsítése igen merész és erősen félrevezető!
Vagy az emberi látás kapcsán:
„ … a szemünkben háromféle színreceptor található, és ezek a fény más-más frekvenciatartományára érzékenyek. Amikor valamilyen színt érzékelünk, a piros, a zöld és a kék receptorok különböző intenzitással vibrálnak, ez pedig egy konkrét pontot jelöl ki a háromdimenziós szín-térben, és ennek eredményeként egy konkrét színt látunk.” (49. oldal)
A könyv egy későbbi szakaszán erre a szerző fel is hívja azért a figyelmet, amikor a modellalkotásról ír:
„Ez a lecsupaszító folyamat olykor túllő a célon, és a túlzottan leegyszerűsített modellek esetében nagyon óvatosnak kell lennünk a való világra levont következtetésekkel. Sokszor megesik, hogy kényelmes olyan feltételezésekbe bocsátkoznunk, amelyek nem teljesen igazak, vagy esetenként akár szemmel láthatóan hamisak.” (202. oldal)
Azonban az olyan fontos fogalmakat, mint a végtelen, kontinuum vagy a különböző leképezések, rendkívül frappánsan sikerült megragadni és hétköznapi példákkal érzékeltetni.
Az algebra területének bemutatását az absztrakció érzékeltetése után a struktúrák világával folytatja. A téma szerteágazó jellegét tekintve csupán ízelítőt ad, amolyan kedvcsinálót:
„Ne aggódj! Nem fogunk végigmenni az összes lehetséges struktúra teljes osztályozásán. Kinek van ennyi ideje? Hiszen rengeteg van belőlük, ami érthető is, mivel a „struktúra” igencsak tág fogalom.” (123. oldal)
Utal fontos struktúrakategóriákra, mint a testekre, gyűrűkre, csoportokra, félcsoportokra, hálókra, hurkokra, grupoidokra, monoidokra stb. De picit konkrétabban főként a halmazokat, gráfokat (irányított- és súlyozott gráfokat, család- és játékfákat), valamint a szimmetria- és tapétacsoportokat mutatja be. Sajnos, a téma változatossága a terjedelmi korlátok miatt nem is igazán jön át az avatatlanabb olvasók számára, pedig igen komoly matematikai terület, és igen könnyen meg lehetne vele ragadni az érdeklődők fantáziáját!
Penrose-féle csempék. (Forrás: https://hu.wikipedia.org/wiki/Penrose-f%C3%A9le_csemp%C3%A9z%C3%A9s.)
Néhány fontosabb fraktál (önhasonló struktúra). Mandelbrot-halmaz, Pagodakarfiol, Sierpinski-piramis, Menger-szivacs, 3 dimenziós Júlia-halmaz. (Forrás: https://elliptigon.com/insideout/, https://hu.wikipedia.org/wiki/Frakt%C3%A1l,
https://hu.m.wikipedia.org/wiki/F%C3%A1jl:Sierpinski_pyramid.png, https://hu.wikipedia.org/wiki/Menger-szivacs,
https://hu.wikipedia.org/wiki/Mandelbrot-halmaz#/media/F%C3%A1jl:Julia_set_(reversed_formula_3D).jpg.)
.jpg){kind=link}
A könyv közepe a matematika történeti és filozófiai vonatkozásait mutatja be, igen szellemesen és stílusosan a Platón által kedvelt párbeszédes formában. Utalásokat vélünk felfedezni Hilbert munkásságára is, de például Gödel név szerint is meg lett említve.
Platón Raffaello festményén (Az Athéni iskola). (Forrás: https://litera.hu/file/slides/1/162587/fe_800_500_platon.jpg.)
David Hilbert és Kurt Gödel. (Forrás: https://www.sapaviva.com/david-hilbert-2/, https://www.ias.edu/scholars/godel.)
A mélyebb filozofikus gondolatok után elég gyakorlatias vizekre evez, alkalmazott matematikai irányba kalauzolja az olvasót, miközben fokozatosan döbbenünk rá, hogy miért. A modellalkotás folyamatát, irányvonalait kezdi boncolgatni sok példán keresztül érzékeltetve a jelentőségét, miközben ott lebeg a kérdés a sorok között az elméleti matematika és az alkalmazott matematika kapcsolatáról. Vajon a tyúk volt előbb vagy a tojás? Az elméleti barangolások után találunk gyakorlati alkalmazásokat, vagy a gyakorlatból alkotjuk meg az elméleti összefüggéseket?
„Vajon a világ miért ennyire fogékony a matematikai modellekre?” (214. oldal)
Az elmélet és a gyakorlat párhuzamba állításából, a topológia, az analízis és az algebra fogalmi építőkockáinak modellbe rendezéséből jelentős filozófiai kérdés bontakozik ki.
„Lehet, hogy azért találunk lépten-nyomon matematikai mintázatokat a természetben, mert a világ matematikából készült. Lehet, hogy az egész világegyetem alapvetően matematikai természetű, és mégiscsak létezik Egy Igazi Modell, amely tökéletesen leírja a működését.” (214. oldal)
A világról végigvezetett gondolatmenetek, eszmefuttatások szimulációkban léptethetők végig, az egészen egyszerűtől a bonyolultabbakig, és máris eljutunk az automaták csodálatos világához! Először egyszerűbb: diszkrét egydimenziós, majd összetettebb példákat tár elénk Beckman, megalapozva John Horton Conway Életjátékának, az egyik leghíresebb automatának a bemutatását.
Alan Turing munkássága, kérdésfeltevései óriási hatással voltak Neumann Jánosra és kollégájára, Stanislaw Ulamra, aki kristályok növekedésének tanulmányozásakor kezdett diszkrét szimulációs rendszert használni. Neumann és Ulam alkotta meg a sejtautomatát, ami 1968-ban megihlette Conwayt. Ez vezetett el a méltán híressé vált diszkrét, kétdimenziós, Turing-teljes sejtautomatájának megalkotásához, ami az Életjáték nevet kapta a biológiai élet folyamatainak tanulmányozásához kapcsolódó párhuzamról (itt játszható).
Néhány jellegzetes mintázat Conway Életjátékából. (Forrás: https://en.wikipedia.org/wiki/Conway%27s_Game_of_Life.)
A könyv még számos egyéb példát említ, többek között a SmoothLife nevű folytonos, kétdimenziós automatát. Ez gyakorlatilag a Conway-féle Életjáték közvetlen, folytonos kiterjesztése.
Néhány érdekes minta a SmoothLife automata projektből. Stephan Rafler munkája. (Forrás: https://sourceforge.net/projects/smoothlife/.)
A különböző egy- és kétdimenziós automaták felvezetése után egy rendkívül lényeges, nagyon komoly, mély témához érkezik a kötet, amelyben összegződik minden felvázolt fogalom, tükröződik az elméleti és alkalmazott matematika minden lényegesebb aspektusa, célja és szépsége. Mindannyiunk számára nagyon hangsúlyos kérdés, akár a matematika aktív művelőiről, akár érdeklődő laikusokról van szó, hiszen az Univerzum és az emberi lét hátterét hivatott elénk tárni (vagy legalábbis sejtetni), nem is akármilyen módon, hanem a részecskefizika standard modelljének folytonos, háromdimenziós automatája által.
„Ráadásul egy szép kerek, érthető történet is szőhető belőle, egy olyan valóságról, amely miriádnyi apró összetevő közös együttműködéséből születik, és ezt sokan gyönyörűnek, lenyűgözőnek tartják, ami alázatra tanít és ámulatba ejt.” (241. oldal)
Noha „rengeteg még a vakfolt” (említi a 241. oldalon):
„Annyi azért bizonyos, hogy érdemes elgondolkodni rajta egy kicsit.” (241. oldal)
Ha csak néhány ember elgondolkodik ezeket olvasva, ha a matematika szerepe és lényege pár ember számára új értelmet nyer, nyugodt szívvel mondhatjuk, hogy a könyv elérte célját!
Dworák Bence
okleveles villamosmérnök, mérnöktanár,
számítógépes és kognitív idegtudomány szakos hallgató (BME)