Folytonos dinamikai rendszerek

Nágel Árpád: Folytonos dinamikai rendszerek. Feladatgyűjtemény, Typotex, Budapest, 2019.

Kis aggodalommal fogadtam el a rovatvezető felkérését egy olyan könyv recenzálására, amelyről azt gondoltam, saját munkáink [6], [7] konkurenciájának tekinthető. Ki fog derülni, hogy nem erről van szó.

A feladatok tárgya a közönséges differenciálegyenletek kvalitatív elmélete; nem értem, miért nem ezt tükrözi a címe. Persze, a dinamikai rendszer sokkal divatosabbnak hangzik (a differenciálegyenletekkel való foglalkozást pedig mintha szégyelleni kellene ma Magyarországon), de sokan sokféleképp használják, ezért nem informatív. Nem beszélve arról, hogy egy rendszer lehet azért folytonos, mert folytonos időben játszódik le, vagy azért, mert állapottere folytonos. Mindezeken felül a rendszer (vagy a modell) lehet determinisztikus vagy sztochasztikus. Az itteni feladatok folytonos idejű, folytonos állapotterű determinisztikus rendszerek közönséges differenciálegyenlettel leírható osztályával foglalkoznak.

Az egyes fejezetek tartalma a következő. Az első két fejezet lineáris és nemlineáris egyenletek stacionárius (másképp: egyensúlyi) pontjának stabilitásával foglalkozik. A harmadik fejezet témája síkbeli rendszerek periodikus megoldásának létezése, illetve ilyen megoldások létezésének kizárása. Az utolsó két fejezet a trajektóriák lokális és globális vizsgálatát tűzi ki célul. (Ebből a rövid áttekintésből is látszik, hogy kicsiny az átfedés a szokásos példatárakkal, speciálisan a [7] példatárral. Legközelebb hozzá az elméletet és feladatokat is tartalmazó [5] jegyzet áll, amely azonban a feladatok részletes kidolgozását nem közli, csupán az eredményeket.) Az egyes fejezetek a szükséges elmélet összefoglalását adják, ezután következik sok-sok feladat, a könyv második része pedig minden feladat részletes megoldását adja, esetenként több változatban is.

Nem lesz nehéz alább dicsérni a gyűjteményt és szerzőjét, ezért először essünk túl néhány kritikai megjegyzésen. Talán sokan kevésbé tartják fontosnak, engem rendkívüli módon bánt a könyv atavisztikus megjelenése. Valaki a TEX birtokában egyszeres és kétszeres aláhúzással jelöli a vektorokat és mátrixokat?! A tételek, állítások, definíciók kiemelésére is aláhúzás helyett jobb a kurziválás vagy a félkövér szedés. Ugyan a szerző különbséget tesz a függvény és a függvényérték között (bár előfordul a $h(x)$ függvény kifejezés), de én magam nem írnék le ilyenfajta kifejezéseket: $u=y/x$ (ehelyett: $u(x):=y(x)/x$ ). A képletek szokásos számozása (1.1.) helyett inkább (1.1). A szerző követi azt a rossz szokást, amely szerint a definíció, tétel, stb. egy mondat utolsó szava, például: Ezt mondja ki az alábbi Tétel. A Jordan-normálformáját kifejezés kicsit tömörre sikerült, jobb lenne ez: Jordan-féle normál alakját. Elmondható, hogy a lektor jól dolgozott, mert konkrét matematikai hibát nehéz találni a jegyzetben; ami fájóan hiányzott: egy korrektor.

Azt gondolom, hogy a megcélzott olvasó túl van az elemeken, ezért fölöslegesnek tartom a rengeteg sok egyszerű számolási feladatot az első két fejezetben.

Az eredetiséget feladatgyűjteményen számon kérni botorság lenne. Gondolom, Pólya és Szegő meglehetősen sok saját munkát is befektetett példatárába, a fő érdemük mégis az volt, hogy az aktuális irodalmat feladtok formájában dolgozták fel. Nágel Árpád sok helyről (jó helyekről) gyűjtött feladatokat, épp ez a legfőbb teljesítménye. Néhány (kidolgozott feladatokat tartalmazó) példatár ugyanis még magyar nyelven is ismert Bajcsayétól [1], [2] és a fájdalmasan korán elhunyt Bege Antalétól (https://hu.wikipedia.org/wiki/Bege_Antal) [3], vagy a különösen gazdag klasszikus [4] gyűjteménytől kezdve a szerző által idézetteken keresztül a miénkig, de egyik sem merészkedik el a haladottabb fejezetekig, amelyekkel kapcsolatos feladatok a különféle speciálizált könyvekből csipegethetők össze, ahogyan ez itt örvendetes módon megtörtént.

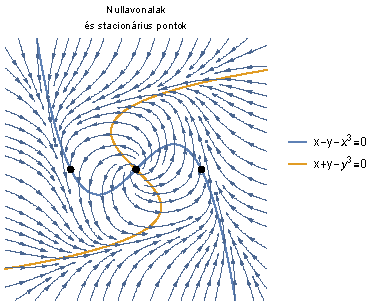
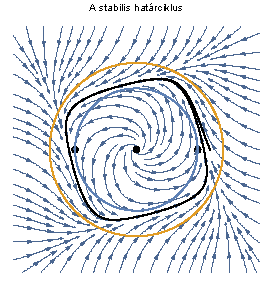
Jó látni egyszerű példákon konkrétan kiszámolt Poincaré-leképezést, stabilis, instabilis és centrális sokaságokat, topologikus ekvivalenciát – még akkor is, ha ezek gyakorlati esetekben nem számolhatók ki.

A példatárban van néhány ábra, általában iránymezők. Az ábráknál és a megoldásoknál is lehetett volna néhány szót ejteni a számítógépes módszerekről, ugyanis az olvasónak mindenképpen azt javasolnám, hogy gép mellett gondolkozzon a feladatokon. (Lásd például a [8] cikket, amely a Routh-Hurwitz-kritérium fájdalmas kiszámítását van hivatva segíteni.)

Apróbb tartalmi megjegyzések: Nem esik arról szó, hogy a stacionárius pontok kiszámolása még polinomiális egyenleteknél is meglehetősen nehéz feladat, viszont meghatározásukban segít a Gröbner-bázisok több mint félévszázados elmélete. Nem a szerző hibája (hanem az elméleté ☺), hogy a kvalitatív elméletben szereplő egyenletek túlnyomó többsége negatív kereszthatást tartalmaz, s emiatt közvetenül nem alkalmazható. Az alkalmazásoknak egy differenciálegyenletekről szóló könyvben nagyobb súlya kellene, hogy legyen.

Az irodalomjegyzék remek útmutató a további elmélyedéshez. Azt gondolom, hogy ezt a recenziót az az olvasó olvassa, aki érdeklődik a téma iránt, ezért a további előrehaladás érdekében kiválóan összeválogatott irodalomjegyzéket a recenzió olvasója számára még néhány tétellel kiegészítem. (Amit nem szabad hiánylistaként felfogni!)

A feladatgyűjtemény matematikai tartalma szerint gazdag és hasznos, messze túlmegy a szokásos bevezető példatárakon, ezért minden alkalmas esetben fogom ajánlani az érdeklődőknek, diákjaimnak, és nagyon remélem, hogy készül belőle további, javított (inkább: szépített) kiadás.

Irodalomjegyzék

[1] Bajcsay P.: Közönséges differenciálegyenletek (Első rész), Műszaki matematikai gyakorlatok B. VII.* (Harmadik kiadás), Tankönyvkiadó, Budapest, 1965.
: [2] Bajcsay P., Fazekas F.: Közönséges differenciálegyenletek (Második rész), Műszaki matematikai gyakorlatok B. VII.** (Második, javított kiadás), Tankönyvkiadó, Budapest, 1969.
: [3] Bege A.: Differenciálegyenletek. Gyakorlatok és feladatok, Kolozsvári Egyetemi Kiadó, Cluj-Napoca, 2008.
: [4] Matvejev, N. M.: Differencálegyenletek. Feladatok és gyakorlatok (6. kiadás), Minszk, Vüséjsaja Skola,1977. (oroszul).
: [5] Simon L. P.: Differenciálegyenletek és dinamikai rendszerek, ELTE Matematikai Intézet, Alkalmazott Analízis és Számításmatematikai Tanszék, 2012. https://simonp.web.elte.hu/files/dinrendjegyzet.pdf,; https://regi.tankonyvtar.hu/hu/tartalom/tamop412A/2011_0025_mat_11/ar01s02.html
: [6] Tóth J., Simon L. P.: Differenciálegyenletek. Bevezetés az elméletbe és az alkalmazásokba (3. kiadás), Typotex, Budapest, 2020.
: [7] Tóth J., Simon L. P., Csikja R.: Differenciálegyenletek. Feladatgyűjtemény, edu.interkonyv.hu
: [8] Tóth, J., Szili, L., Zachár, A.: Stability of polynomials Math. Educ. Res. 7 (2), 5–12.