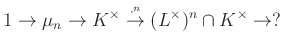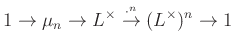1. Kvaternióktól a centrális egyszerű algebrákig
A történet ott kezdődik, hogy a legenda szerint az 1840-es évek elején Hamilton ír matematikus azon gondolkozott, hogyan tudna a háromdimenziós vektorokon egy „jól működő” szorzást definiálni (a kétdimenziós sík és a komplex számok azonosításának mintájára). Hosszas gondolkozás után 1843 októberében rájött, hogy ugyan ez három dimenzióban nem lehetséges, négy dimenzióban viszont igen. A Hamilton-féle kvaterniók a ![]() alakú formális kifejezések, ahol
alakú formális kifejezések, ahol ![]() , az
, az ![]() szimbólumokkal pedig a következőképpen kell számolni:
szimbólumokkal pedig a következőképpen kell számolni:
Láthatóan a fenti szorzás nem kommutatív, ugyanakkor a disztributivitás megtartásával ki lehet terjeszteni az összes ![]() alakú kifejezésre úgy, hogy az asszociativitást megőrizzük. A Hamilton-féle kvaterniók egy
alakú kifejezésre úgy, hogy az asszociativitást megőrizzük. A Hamilton-féle kvaterniók egy ![]() ferdetestet alkotnak (az alapműveletek: összeadás, kivonás, szorzás, és
ferdetestet alkotnak (az alapműveletek: összeadás, kivonás, szorzás, és ![]() elemmel való osztás elvégezhetők azzal a kitétellel, hogy a szorzás, mint láttuk, nem kommutatív). Ráadásul a „tisztán képzetes” kvaterniókat azonosíthatjuk a háromdimenziós tér vektoraival és a kvaterniószorzás segítségével kifejezhető a skaláris és vektoriális szorzás is. Hamiltont a fizikai alkalmazások érdekelték, de hogy jön ide az aritmetika?
elemmel való osztás elvégezhetők azzal a kitétellel, hogy a szorzás, mint láttuk, nem kommutatív). Ráadásul a „tisztán képzetes” kvaterniókat azonosíthatjuk a háromdimenziós tér vektoraival és a kvaterniószorzás segítségével kifejezhető a skaláris és vektoriális szorzás is. Hamiltont a fizikai alkalmazások érdekelték, de hogy jön ide az aritmetika?
Ahhoz, hogy elinduljunk ezen az úton, az első észrevétel a következő: a ![]() együtthatókat nemcsak a valós, hanem tetszőleges testből vehetjük. Ha például komplex együtthatókat választunk, akkor a kapott gyűrű izomorf lesz a
együtthatókat nemcsak a valós, hanem tetszőleges testből vehetjük. Ha például komplex együtthatókat választunk, akkor a kapott gyűrű izomorf lesz a ![]() feletti
feletti ![]() -es mátrixok
-es mátrixok ![]() gyűrűjével a
gyűrűjével a
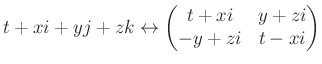
azonosításon keresztül (vegyük észre, hogy a mátrixban szereplő ![]() egy komplex szám — melynek négyzete
egy komplex szám — melynek négyzete ![]() —, ami nem tévesztendő össze az
—, ami nem tévesztendő össze az ![]() kvaternióval: a történeti hűség kedvéért most megengedjük ezt a pici jelölésbeli következetlenséget). Mint látni fogjuk, a
kvaternióval: a történeti hűség kedvéért most megengedjük ezt a pici jelölésbeli következetlenséget). Mint látni fogjuk, a ![]() gyűrű a valósak felett egy csavart formája a kétszer kettes mátrixok gyűrűjének:
gyűrű a valósak felett egy csavart formája a kétszer kettes mátrixok gyűrűjének: ![]() fölött már izomorffá válnak.
fölött már izomorffá válnak.
A centrális egyszerű algebrák (melyek a könyv fő témáját alkotják) nem mások, mint az ![]() -es mátrixgyűrűk csavart formái nem feltétlenül algebrailag zárt testek felett (tetszőleges
-es mátrixgyűrűk csavart formái nem feltétlenül algebrailag zárt testek felett (tetszőleges ![]() -re). A precíz definíció a következő: Legyen
-re). A precíz definíció a következő: Legyen ![]() test,
test, ![]() pedig végesdimenziós
pedig végesdimenziós ![]() -algebra (azaz
-algebra (azaz ![]() olyan egységelemes gyűrű, aminek
olyan egységelemes gyűrű, aminek ![]() részgyűrűje úgy, hogy
részgyűrűje úgy, hogy ![]() minden eleme felcserélhető
minden eleme felcserélhető ![]() minden elemével, és
minden elemével, és ![]() végesdimenziós, mint
végesdimenziós, mint ![]() feletti vektortér). Az
feletti vektortér). Az ![]() algebrát akkor hívjuk centrális egyszerű algebrának (
algebrát akkor hívjuk centrális egyszerű algebrának (![]() felett), ha
felett), ha ![]() egyszerű (azaz nincs nemtriviális kétoldali ideálja) és
egyszerű (azaz nincs nemtriviális kétoldali ideálja) és ![]() a centruma (azaz a minden
a centruma (azaz a minden ![]() -belivel felcserélhető elemek részgyűrűje) megegyezik
-belivel felcserélhető elemek részgyűrűje) megegyezik ![]() -val. Wedderburn klasszikus tétele szerint minden centrális egyszerű algebra izomorf egy
-val. Wedderburn klasszikus tétele szerint minden centrális egyszerű algebra izomorf egy ![]() ferdetest feletti
ferdetest feletti ![]() teljes mátrixgyűrűvel (alkalmas
teljes mátrixgyűrűvel (alkalmas ![]() -re). Sőt, ha a
-re). Sőt, ha a ![]() alaptest algebrailag zárt, akkor
alaptest algebrailag zárt, akkor ![]() , azaz algebrailag zárt test fölött csak a teljes mátrixgyűrűk a centrális egyszerű algebrák. Viszont ha
, azaz algebrailag zárt test fölött csak a teljes mátrixgyűrűk a centrális egyszerű algebrák. Viszont ha ![]() nem algebrailag zárt (és az egyszerűség kedvéért a továbbiakban tegyük fel, hogy karakterisztikája
nem algebrailag zárt (és az egyszerűség kedvéért a továbbiakban tegyük fel, hogy karakterisztikája ![]() ), akkor léteznek úgynevezett nem hasadó centrális egyszerű algebrák: a
), akkor léteznek úgynevezett nem hasadó centrális egyszerű algebrák: a ![]() -dimenziós esetben az összes ilyen algebrát megkaphatjuk a szokásos kvaterniókhoz hasonló konstrukcióval: Vegyünk két nullától különböző
-dimenziós esetben az összes ilyen algebrát megkaphatjuk a szokásos kvaterniókhoz hasonló konstrukcióval: Vegyünk két nullától különböző ![]() elemet, és tekintsük a
elemet, és tekintsük a ![]() alakú formális kifejezéseket, ahol
alakú formális kifejezéseket, ahol ![]() , az
, az ![]() szimbólumokra pedig legyen:
szimbólumokra pedig legyen:
Az így konstruált ún. (általánosított) kvaternióalgebrát ![]() -vel, vagy ha a
-vel, vagy ha a ![]() alaptestet is hangsúlyozni akarjuk, akkor
alaptestet is hangsúlyozni akarjuk, akkor ![]() -val jelöljük. Azt mondjuk, hogy az
-val jelöljük. Azt mondjuk, hogy az ![]() testbővítés felhasítja az
testbővítés felhasítja az ![]() kvaternióalgebrát (vagy általánosabban az
kvaternióalgebrát (vagy általánosabban az ![]() centrális egyszerű algebrát), ha
centrális egyszerű algebrát), ha ![]() izomorf
izomorf ![]() -lel (illetve ha
-lel (illetve ha ![]() izomorf
izomorf ![]() -lel valamilyen
-lel valamilyen ![]() -re).1 Nem nehéz belátni (a komplex együtthatós kvaterniókhoz hasonlóan), hogy minden kvaternióalgebrát felhasít egy alkalmas másodfokú bővítés: elegendő
-re).1 Nem nehéz belátni (a komplex együtthatós kvaterniókhoz hasonlóan), hogy minden kvaternióalgebrát felhasít egy alkalmas másodfokú bővítés: elegendő ![]() -ból (vagy
-ból (vagy ![]() -ből, esetleg
-ből, esetleg ![]() -ből) négyzetgyököt vonni. Az is világos, hogy az
-ből) négyzetgyököt vonni. Az is világos, hogy az ![]() és
és ![]() struktúrakonstansokat nem határozza meg egyértelműen a kvaternióalgebra izomorfiaosztálya: pl.
struktúrakonstansokat nem határozza meg egyértelműen a kvaternióalgebra izomorfiaosztálya: pl. ![]() , sőt
, sőt ![]() (
( ![]() tetszőleges).
tetszőleges).
Ahhoz, hogy ezt a jelenséget mélyebben megértsük és osztályozni tudjuk az adott ![]() test feletti centrális egyszerű algebrákat, segítségül kell hívnunk a Galois-elméletet.
test feletti centrális egyszerű algebrákat, segítségül kell hívnunk a Galois-elméletet.
2. Galois-kohomológia kommutatív együtthatókkal
Motivációként kezdjük egy klasszikus példával. Az egyenletek gyökjelekkel való megoldhatóságának elméletéből ismeretes a következő
Tétel. Legyen ![]() olyan test, melyben van primitív
olyan test, melyben van primitív ![]() -edik egységgyök (speciálisan
-edik egységgyök (speciálisan ![]() karakterisztikája nem osztja
karakterisztikája nem osztja ![]() -et), továbbá legyen
-et), továbbá legyen ![]() olyan Galois-bővítés, melynek
olyan Galois-bővítés, melynek ![]() Galois-csoportja2 az
Galois-csoportja2 az ![]() -edrendű ciklikus csoport. Ekkor
-edrendű ciklikus csoport. Ekkor ![]() nem más mint egy alkalmas
nem más mint egy alkalmas ![]() elem (egyik)
elem (egyik) ![]() -edik gyökével való bővítése.
-edik gyökével való bővítése.
Hogyan bizonyítjuk ezt koncepciózusan? A gondolatmenet a következő: egy olyan ![]() elemet szeretnénk találni, ami
elemet szeretnénk találni, ami ![]() -ban nem
-ban nem ![]() -edik hatvány, sőt nem is
-edik hatvány, sőt nem is ![]() -adik hatvány semmilyen
-adik hatvány semmilyen ![]() -re, viszont
-re, viszont ![]() -ben már
-ben már ![]() -edik hatvány. Fordítsuk ezt le a testek nemnulla elemeinek szorzáscsoportjára! Az
-edik hatvány. Fordítsuk ezt le a testek nemnulla elemeinek szorzáscsoportjára! Az ![]() multiplikatív csoporton az
multiplikatív csoporton az ![]() -edik hatványra emelés egy csoporthomomorfizmus, ezért az
-edik hatványra emelés egy csoporthomomorfizmus, ezért az ![]() -edik hatványok egy
-edik hatványok egy ![]() részcsoportot alkotnak. Tehát
részcsoportot alkotnak. Tehát ![]() -nak egyszerre kell
-nak egyszerre kell ![]() -ben és a
-ben és a ![]() részcsoportban is benne lennie. Mit jelent ugyanakkor, hogy
részcsoportban is benne lennie. Mit jelent ugyanakkor, hogy ![]() -ban még nem
-ban még nem ![]() -edik hatvány az
-edik hatvány az ![]() elem? Azt, hogy nincs benne a
elem? Azt, hogy nincs benne a ![]() részcsoportban. Sőt, az is kellene, hogy
részcsoportban. Sőt, az is kellene, hogy ![]() semmilyen
semmilyen ![]() -re sincs benne
-re sincs benne ![]() -ban, hiszen ha
-ban, hiszen ha ![]() akkor az
akkor az ![]() -val való bővítés
-val való bővítés ![]() -nél kisebb (
-nél kisebb (![]() ) fokú lenne. Vegyük észre, hogy ezt átfogalmazhatjuk úgy is, hogy
) fokú lenne. Vegyük észre, hogy ezt átfogalmazhatjuk úgy is, hogy ![]() sem
sem ![]() -edik hatvány
-edik hatvány ![]() -ban. Ez pedig másszóval azt jelenti, hogy
-ban. Ez pedig másszóval azt jelenti, hogy ![]() mellékosztálya az
mellékosztálya az ![]() faktorcsoportban egy
faktorcsoportban egy ![]() -edrendű elem (az világos, hogy az
-edrendű elem (az világos, hogy az ![]() -edik hatványa benne van
-edik hatványa benne van ![]() -ben). Tehát az
-ben). Tehát az ![]() -edik hatványra emelés, mint
-edik hatványra emelés, mint 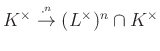 leképezés komagját szeretnénk megérteni, azaz a kérdés az, hogy a
leképezés komagját szeretnénk megérteni, azaz a kérdés az, hogy a
sorozatban mit kell a ![]() helyére írnunk, hogy egzakt3 sorozatot kapjunk (itt
helyére írnunk, hogy egzakt3 sorozatot kapjunk (itt ![]() az
az ![]() -edik egységgyökök csoportját jelöli, ami nem más, mint az
-edik egységgyökök csoportját jelöli, ami nem más, mint az ![]() -edik hatványra emelés magja). A
-edik hatványra emelés magja). A ![]() Galois-csoport a Galois-elmélet főtételén keresztül jön a képbe: ennek segítségével tudjuk karakterizálni
Galois-csoport a Galois-elmélet főtételén keresztül jön a képbe: ennek segítségével tudjuk karakterizálni ![]() azon elemeit, melyek benne vannak a szűkebb
azon elemeit, melyek benne vannak a szűkebb ![]() testben: ezek pontosan azok az elemek, melyeket a
testben: ezek pontosan azok az elemek, melyeket a ![]() csoport minden eleme (mint
csoport minden eleme (mint ![]() automorfizmusa) helybenhagy. (Ez annak az általánosítása, hogy egy komplex szám pontosan akkor valós, ha megegyezik a konjugáltjával.) Tehát az ([1]) sorozatot megkaphatjuk úgy, hogy a
automorfizmusa) helybenhagy. (Ez annak az általánosítása, hogy egy komplex szám pontosan akkor valós, ha megegyezik a konjugáltjával.) Tehát az ([1]) sorozatot megkaphatjuk úgy, hogy a
rövid egzakt sorozat elemeinek vesszük a ![]() -invariánsait (a
-invariánsait (a ![]() -invariáns elemek részcsoportját a továbbiakban
-invariáns elemek részcsoportját a továbbiakban ![]() -vel jelöljük). Így a kérdést arra a problémára fordítottuk le, hogy a
-vel jelöljük). Így a kérdést arra a problémára fordítottuk le, hogy a ![]() -invariánsok képzése mennyire rontja el az egzaktságot: ezt méri a
-invariánsok képzése mennyire rontja el az egzaktságot: ezt méri a ![]() Galois-kohomológia csoport. Hogyan tudjuk ezt a kohomológiacsoportot megkonstruálni? Miért csak
Galois-kohomológia csoport. Hogyan tudjuk ezt a kohomológiacsoportot megkonstruálni? Miért csak ![]() -től (és nem
-től (és nem ![]() -től vagy
-től vagy ![]() -től) „függ” a
-től) „függ” a ![]() helyére írandó csoport?
helyére írandó csoport?
Ennek megválaszolásához kicsit általánosabban vegyük ![]() -hatással ellátott (additívan írt) Abel csoportoknak egy
-hatással ellátott (additívan írt) Abel csoportoknak egy ![]() rövid egzakt sorozatát, azaz
rövid egzakt sorozatát, azaz ![]() egy
egy ![]() -invariáns részcsoport
-invariáns részcsoport ![]() -ben,
-ben, ![]() pedig a faktorcsoport. Ha veszünk egy
pedig a faktorcsoport. Ha veszünk egy ![]() invariáns elemet, mi az oka annak, hogy az nem egy
invariáns elemet, mi az oka annak, hogy az nem egy ![]() -beli invariáns elemből jön? Az egzaktság miatt van egy
-beli invariáns elemből jön? Az egzaktság miatt van egy ![]() elem, ami erre a
elem, ami erre a ![]() -re képződik, de csak annyit tudunk, hogy
-re képződik, de csak annyit tudunk, hogy ![]() csak modulo
csak modulo ![]() lesz
lesz ![]() -invariáns, azaz tetszőleges
-invariáns, azaz tetszőleges ![]() -re
-re ![]() . Tehát ez definiál egy
. Tehát ez definiál egy ![]() leképezést, mégpedig
leképezést, mégpedig ![]() .
.
Hogy viselkedik ez a függvény ![]() -beli művelettel?
-beli művelettel?
![]() : az ilyen tulajdonsággal bíró függvényeket hívják
: az ilyen tulajdonsággal bíró függvényeket hívják ![]() -kociklusnak vagy keresztezett homomorfizmusnak. Ha
-kociklusnak vagy keresztezett homomorfizmusnak. Ha ![]() rögzített, mennyire függ
rögzített, mennyire függ ![]() a
a ![]() őskép választásától? Ha
őskép választásától? Ha ![]() egy másik őskép, akkor
egy másik őskép, akkor ![]() , és
, és ![]() , tehát egy
, tehát egy ![]() elemmel definiált
elemmel definiált ![]() függvényben térnek el (ún. principális keresztezett homomorfizmus). A
függvényben térnek el (ún. principális keresztezett homomorfizmus). A ![]() első kohomológiacsoportot tehát a
első kohomológiacsoportot tehát a
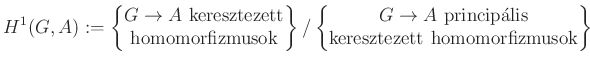
faktorcsoportként definiálhatjuk.
A mi esetünkben tehát milyen csoport lesz ![]() ? Mivel a
? Mivel a ![]() alaptestünk tartalmazza az
alaptestünk tartalmazza az ![]() -edik egységgyököket, ezért a
-edik egységgyököket, ezért a ![]() -hatás triviális
-hatás triviális ![]() -en. Speciálisan minden keresztezett homomorfizmus egy igazi homomorfizmus, hiszen
-en. Speciálisan minden keresztezett homomorfizmus egy igazi homomorfizmus, hiszen ![]() , sőt, a principális keresztezett homomorfizmusok mind triviálisak. Viszont
, sőt, a principális keresztezett homomorfizmusok mind triviálisak. Viszont ![]() és
és ![]() is
is ![]() -edrendű ciklikus, ezért
-edrendű ciklikus, ezért ![]() is az. Ahhoz, hogy az eredeti problémára választ adjunk, már csak azt kell látni, hogy a sorozat következő tagja, jelesül
is az. Ahhoz, hogy az eredeti problémára választ adjunk, már csak azt kell látni, hogy a sorozat következő tagja, jelesül ![]() triviális — ez pedig nem más, mint Hilbert
triviális — ez pedig nem más, mint Hilbert ![]() -es tétele.4 Így azt kaptuk, hogy az
-es tétele.4 Így azt kaptuk, hogy az ![]() faktorcsoport izomorf
faktorcsoport izomorf ![]() -nel, azaz az
-nel, azaz az ![]() -edrendű ciklikus csoporttal. Speciálisan létezik a kívánt
-edrendű ciklikus csoporttal. Speciálisan létezik a kívánt ![]() elem.
elem.
A homologikus algebra eszközeivel definiálhatók a magasabb fokú ![]() (
(![]() ) kohomológiacsoportok is, mint a
) kohomológiacsoportok is, mint a ![]() funktor ún. derivált funktorai. Itt
funktor ún. derivált funktorai. Itt ![]() olyan Abel csoport, melyen a
olyan Abel csoport, melyen a ![]() csoport automorfizmusokkal hat. Az általános elméletből következik, hogy minden
csoport automorfizmusokkal hat. Az általános elméletből következik, hogy minden ![]() rövid egzakt sorozathoz tartozik egy
rövid egzakt sorozathoz tartozik egy
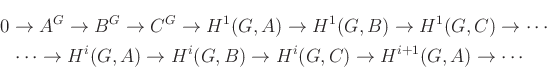
kohomologikus hosszú egzakt sorozat.
3. Centrális egyszerű algebrák és a Brauer-csoport
A fentiek mintájára klasszifikálhatjuk az ![]() -edfokú (azaz a
-edfokú (azaz a ![]() alaptest felett
alaptest felett ![]() -dimenziós) centrális egyszerű algebrákat is. Vegyünk egy
-dimenziós) centrális egyszerű algebrákat is. Vegyünk egy ![]() centrális egyszerű algebrát
centrális egyszerű algebrát ![]() fölött. Ekkor van olyan
fölött. Ekkor van olyan ![]() véges Galois-bővítés (
véges Galois-bővítés (![]() ), melyhez létezik
), melyhez létezik ![]() izomorfizmus. Vegyük észre, hogy ez a — nemkanonikus — azonosítás (általában) nem
izomorfizmus. Vegyük észre, hogy ez a — nemkanonikus — azonosítás (általában) nem ![]() -ekvivariáns a két oldalon levő
-ekvivariáns a két oldalon levő ![]() -hatásra nézve! Ugyanis
-hatásra nézve! Ugyanis ![]() -ben a
-ben a ![]() -invariáns rész épp
-invariáns rész épp ![]() , az
, az ![]() teljes mátrixgyűrűben viszont
teljes mátrixgyűrűben viszont ![]() — melyek nemizomorfak, hacsak
— melyek nemizomorfak, hacsak ![]() nem hasad már
nem hasad már ![]() fölött is. Éppen a
fölött is. Éppen a ![]() -ekvivarianciának ez a hiánya definiál egy
-ekvivarianciának ez a hiánya definiál egy ![]() keresztezett homomorfizmust: Ha van egy
keresztezett homomorfizmust: Ha van egy ![]() elemünk, akkor megnézhetjük, mennyiben tér el a
elemünk, akkor megnézhetjük, mennyiben tér el a ![]() -hatás a két oldalon: az
-hatás a két oldalon: az
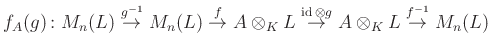
izomorfizmus már ![]() -lineáris lesz, azaz egy automorfizmusát adja
-lineáris lesz, azaz egy automorfizmusát adja ![]() -nek. Node
-nek. Node ![]() minden automorfizmusa belső, azaz
minden automorfizmusa belső, azaz ![]() , ahol
, ahol ![]() az
az ![]() -edfokú általános lineáris csoportot jelöli (tehát az
-edfokú általános lineáris csoportot jelöli (tehát az ![]() -es
-es ![]() -beli együtthatós invertálható mátrixok csoportját),
-beli együtthatós invertálható mátrixok csoportját), ![]() pedig ennek a centrumát, azaz a skalármátrixok részcsoportját. A technikai probléma itt az, hogy mivel
pedig ennek a centrumát, azaz a skalármátrixok részcsoportját. A technikai probléma itt az, hogy mivel ![]() nem kommutatív, a
nem kommutatív, a ![]() keresztezett homomorfizmusok nem alkotnak csoportot! Viszont ekvivalenciarelációt megadhatunk rajtuk: két keresztezett homomorfizmus ekvivalens, ha egy principális keresztezett homomorfizmusban térnek el. Az ekvivalenciaosztályok csak egy halmazt alkotnak, amin az egyetlen struktúra, hogy van egy kitüntetett eleme: jelesül a triviális keresztezett homomorfizmus osztálya. Ha
keresztezett homomorfizmusok nem alkotnak csoportot! Viszont ekvivalenciarelációt megadhatunk rajtuk: két keresztezett homomorfizmus ekvivalens, ha egy principális keresztezett homomorfizmusban térnek el. Az ekvivalenciaosztályok csak egy halmazt alkotnak, amin az egyetlen struktúra, hogy van egy kitüntetett eleme: jelesül a triviális keresztezett homomorfizmus osztálya. Ha ![]() -nel jelöljük azon
-nel jelöljük azon ![]() feletti
feletti ![]() fokú centrális egyszerű algebrák izomorfiaosztályait, melyek
fokú centrális egyszerű algebrák izomorfiaosztályait, melyek ![]() fölött trivializálódnak, akkor a fenti megfeleltetés megad egy
fölött trivializálódnak, akkor a fenti megfeleltetés megad egy ![]() pontozott terek közti bijekciót. (Itt
pontozott terek közti bijekciót. (Itt ![]() -ben a kitüntetett elem az
-ben a kitüntetett elem az ![]() mátrixgyűrű osztálya.)
mátrixgyűrű osztálya.)
Viszont mi nemcsak azon centrális algebrákat szeretnénk osztályozni, melyeket egy konkrét ![]() bővítés felhasít, sőt az
bővítés felhasít, sőt az ![]() fokot sem szeretnénk rögzíteni. Továbbá szeretnénk az
fokot sem szeretnénk rögzíteni. Továbbá szeretnénk az ![]() mátrixgyűrűt minden
mátrixgyűrűt minden ![]() -re triviálisnak tekinteni. A cél az, hogy egy (Abel-)csoport klasszifikálja ezeket az objektumokat. A természetes művelet a centrális egyszerű algebrákon a
-re triviálisnak tekinteni. A cél az, hogy egy (Abel-)csoport klasszifikálja ezeket az objektumokat. A természetes művelet a centrális egyszerű algebrákon a ![]() feletti tenzorszorzás, melyre nézve a centrális egyszerű algebrák izomorfiaosztályai egy
feletti tenzorszorzás, melyre nézve a centrális egyszerű algebrák izomorfiaosztályai egy 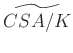 kommutatív egységelemes félcsoportot alkotnak. Az
kommutatív egységelemes félcsoportot alkotnak. Az ![]() és
és ![]() centrális egyszerű algebrákat Brauer-ekvivalensnek hívjuk, ha van olyan
centrális egyszerű algebrákat Brauer-ekvivalensnek hívjuk, ha van olyan ![]() , illetve
, illetve ![]() pozitív egész, melyekre
pozitív egész, melyekre ![]() izomorf
izomorf ![]() -val. A
-val. A ![]() csoportot a
csoportot a ![]() fölötti centrális egyszerű algebrák ekvivalenciosztályai alkotják a tenzorszorzásra nézve. Ezt nevezzük a
fölötti centrális egyszerű algebrák ekvivalenciosztályai alkotják a tenzorszorzásra nézve. Ezt nevezzük a ![]() test (abszolút) Brauer-csoportjának, mely rendelkezik azzal az „univerzális” tulajdonsággal, hogy
test (abszolút) Brauer-csoportjának, mely rendelkezik azzal az „univerzális” tulajdonsággal, hogy 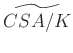 minden Abel-csoportba képező félcsoporthomomorfizmusa, mely az
minden Abel-csoportba képező félcsoporthomomorfizmusa, mely az ![]() mátrixgyűrűket az egységelembe küldi, átfaktorizálódik
mátrixgyűrűket az egységelembe küldi, átfaktorizálódik ![]() -n. Az olvasóban felmerülhet a kérdés, miért lesz
-n. Az olvasóban felmerülhet a kérdés, miért lesz ![]() csoport: miért van inverz? Ezt viszonylag könnyű látni: egy
csoport: miért van inverz? Ezt viszonylag könnyű látni: egy ![]() centrális egyszerű algebra Brauer-osztályának az inverze az
centrális egyszerű algebra Brauer-osztályának az inverze az ![]() oppozit algebra lesz (az az algebra, ami az összeadásra nézve ugyanaz az Abel csoport, mint
oppozit algebra lesz (az az algebra, ami az összeadásra nézve ugyanaz az Abel csoport, mint ![]() , de a szorzást „fordítva” értelmezzük, azaz
, de a szorzást „fordítva” értelmezzük, azaz ![]() és
és ![]() szorzata
szorzata ![]() -ben
-ben ![]() lesz). Ennek az az oka, hogy
lesz). Ennek az az oka, hogy ![]() hat saját magán a bal- és a jobb szorzással is, ami megad egy
hat saját magán a bal- és a jobb szorzással is, ami megad egy ![]() gyűrűhomomorfizmust — ez pedig dimenzióokokból bijektív.
gyűrűhomomorfizmust — ez pedig dimenzióokokból bijektív.
A Brauer-csoport kohomologikus interpretációjához a következő módon juthatunk el. Ha ![]() jelöli a
jelöli a ![]() test abszolút Galois-csoportját5, akkor
test abszolút Galois-csoportját5, akkor
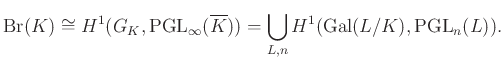
A jobb oldalon álló kohomológiateret — ami a priori csak egy pontozott halmaz, nincs rajta csoportstruktúra — vagy a ![]() provéges csoport folytonos
provéges csoport folytonos ![]() -kociklusainak ekvivalenciaosztályaiként, vagy felszálló unióként interpretálhatjuk. A kommutatív együtthatós kohomológiacsoportokkal ellentétben nemkommutatív együtthatókkal csak az alacsony fokú kohomológiákat tudjuk definiálni, ráadásul, azok sem alkotnak csoportot, csak pontozott teret. Ugyanakkor — ameddig definiálva van, addig — létezik egy kohomologikus hosszú egzakt sorozat is nemkommutatív együtthatókkal. Ahhoz, hogy ezt értelmezni tudjuk, meg kell mondanunk, mit értünk pontozott terek egy
-kociklusainak ekvivalenciaosztályaiként, vagy felszálló unióként interpretálhatjuk. A kommutatív együtthatós kohomológiacsoportokkal ellentétben nemkommutatív együtthatókkal csak az alacsony fokú kohomológiákat tudjuk definiálni, ráadásul, azok sem alkotnak csoportot, csak pontozott teret. Ugyanakkor — ameddig definiálva van, addig — létezik egy kohomologikus hosszú egzakt sorozat is nemkommutatív együtthatókkal. Ahhoz, hogy ezt értelmezni tudjuk, meg kell mondanunk, mit értünk pontozott terek egy
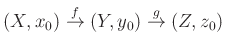
sorozatának egzaktságán. Ezt a lehető legnaivabb módon definiáljuk: az ![]() -nál való egzaktság azt jelenti, hogy egy
-nál való egzaktság azt jelenti, hogy egy ![]() -ra
-ra ![]() (azaz
(azaz ![]() benne van
benne van ![]() magjában) akkor és csak akkor, ha van olyan
magjában) akkor és csak akkor, ha van olyan ![]() , amire
, amire ![]() (azaz
(azaz ![]() benne van
benne van ![]() képében). Vegyük észre, hogy a mag trivialitásából — csoportok közti leképezésekkel ellentétben — még nem következik, hogy a leképezés injektív. Az
képében). Vegyük észre, hogy a mag trivialitásából — csoportok közti leképezésekkel ellentétben — még nem következik, hogy a leképezés injektív. Az ![]() rövid egzakt sorozathoz akkor tartozik kohomologikus hosszú egzakt sorozat, ha
rövid egzakt sorozathoz akkor tartozik kohomologikus hosszú egzakt sorozat, ha ![]() benne van
benne van ![]() centrumában (speciálisan
centrumában (speciálisan ![]() kommutatív). Viszont a
kommutatív). Viszont a
rövid egzakt sorozat valóban teljesíti ezt a feltételt, és a hozzá tartozó ![]() -kohomológiák hosszú egzakt sorozata az
-kohomológiák hosszú egzakt sorozata az
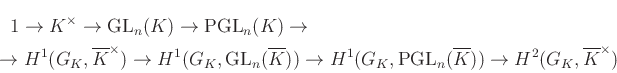
alakot ölti. Így ![]() -nel tartva a végtelenbe és felszálló uniót véve kapunk egy
-nel tartva a végtelenbe és felszálló uniót véve kapunk egy
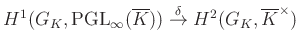
leképezést, melyről megmutatható6, hogy bijektív. Ebben a bijekcióban az a szerencsés, hogy mivel ![]() kommutatív, ezért a jobb oldal Abel-csoport. Továbbá a
kommutatív, ezért a jobb oldal Abel-csoport. Továbbá a ![]() bijekció csoportizomorfizmus!
bijekció csoportizomorfizmus!
4. Ciklikus algebrák és a Merkurjev—Szuszlin-tétel
Szamuely Tamás és Philippe Gille könyvének (egyik) fő tétele (mely Merkurjev és Szuszlin nevéhez fűződik7) egyfajta struktúratétel centrális egyszerű algebrákra. Kimondásához szükségünk lesz az ún. ciklikus algebrák fogalmára, melyek speciális centrális egyszerű algebrák, bizonyos szempontból a kvaternióalgebrák magasabb dimenziós közvetlen általánosításai. Az egyszerűség kedvéért tegyük fel, hogy a ![]() alaptest tartalmaz egy
alaptest tartalmaz egy ![]() primitív
primitív ![]() -edik egységgyököt valamilyen
-edik egységgyököt valamilyen ![]() -re. Ekkor az
-re. Ekkor az ![]() konstansokkal definiált
konstansokkal definiált ![]() -edfokú
-edfokú ![]() ciklikus algebrát az
ciklikus algebrát az
prezentációval adhatjuk meg. Valóban, a kvaternióalgebrák ennek speciális esetei ![]() és
és ![]() választással. Amennyiben
választással. Amennyiben ![]() nem tartalmaz primitív
nem tartalmaz primitív ![]() -edik egységgyököt, akkor olyan
-edik egységgyököt, akkor olyan ![]() bővítést kell választanunk (
bővítést kell választanunk (![]() helyett), melynek a Galois-csoportja
helyett), melynek a Galois-csoportja ![]() -edrendű ciklikus csoport valamely
-edrendű ciklikus csoport valamely ![]() generátorral, a ciklikus algebránk pedig az
generátorral, a ciklikus algebránk pedig az ![]() algebra azokkal a relációkkal, hogy
algebra azokkal a relációkkal, hogy ![]() , és
, és ![]() nem felcserélhető
nem felcserélhető ![]() elemeivel: jelesül az
elemeivel: jelesül az ![]() -nal való konjugálás
-nal való konjugálás ![]() -en épp a
-en épp a ![]() testautomorfizmus.
testautomorfizmus.
Tétel. (Merkurjev—Szuszlin) Tegyük fel, hogy ![]() -ban van egy
-ban van egy ![]() primitív
primitív ![]() -edik egységgyök, és
-edik egységgyök, és ![]() egy centrális egyszerű
egy centrális egyszerű ![]() -algebra úgy, hogy
-algebra úgy, hogy ![]() Brauer-csoportbeli osztályának rendje (azaz
Brauer-csoportbeli osztályának rendje (azaz ![]() periódusa) osztja
periódusa) osztja ![]() -et. Ekkor
-et. Ekkor ![]() Brauer-ekvivalens néhány
Brauer-ekvivalens néhány ![]() -edfokú ciklikus algebra
-edfokú ciklikus algebra
tenzorszorzatával.
A fenti tétel következménye, hogy (legalábbis 0 karakterisztikában) minden centrális egyszerű algebra felhasad egy alkalmas feloldható Galois-bővítés felett (azaz olyan Galois bővítés felett, melynek Galois-csoportja feloldható). Ehhez először azt kell látnunk, hogy ![]() torziócsoport: nincs benne végtelen rendű elem. Ugyanis ha
torziócsoport: nincs benne végtelen rendű elem. Ugyanis ha ![]() centrális egyszerű algebra, ahol
centrális egyszerű algebra, ahol ![]() foka
foka ![]() (ezt a számot hívjuk
(ezt a számot hívjuk ![]() indexének), akkor megmutatható, hogy
indexének), akkor megmutatható, hogy ![]()
![]() -edik tenzorhatványa felhasad, azaz
-edik tenzorhatványa felhasad, azaz ![]() periódusa osztója az indexének. Tehát ha
periódusa osztója az indexének. Tehát ha ![]()
![]() indexű centrális egyszerű algebra, akkor a
indexű centrális egyszerű algebra, akkor a ![]() bővítés fölött (ahol
bővítés fölött (ahol ![]() primitív
primitív ![]() -edik egységgyök)
-edik egységgyök) ![]() Brauer-ekvivalens lesz egy ([5]) alakú algebrával, ami pedig a
Brauer-ekvivalens lesz egy ([5]) alakú algebrával, ami pedig a ![]() bővítés fölött hasad, így persze
bővítés fölött hasad, így persze ![]() is. A
is. A ![]() Galois csoport viszont feloldható. Megjegyezzük, hogy erre a — viszonylag elemien megfogalmazható — következményre nem ismert elemi bizonyítás.
Galois csoport viszont feloldható. Megjegyezzük, hogy erre a — viszonylag elemien megfogalmazható — következményre nem ismert elemi bizonyítás.
A Merkurjev—Szuszlin-tétel bizonyítása nagyon mély eszközöket használ: algebrai geometriai-, és algebrai ![]() -elméleti technikákat is, melyeket Szamuely és Gille — sokszor az eredeti forrástól eltérő módon — felépítenek a könyvben. Az első lépésként ugyanakkor az alábbiakban vázoljuk a kapcsolatot a 2. fejezetben a feloldható bővítésekre alkalmazott Kummer-elmélettel. Ha a ([2]) sorozatban az
-elméleti technikákat is, melyeket Szamuely és Gille — sokszor az eredeti forrástól eltérő módon — felépítenek a könyvben. Az első lépésként ugyanakkor az alábbiakban vázoljuk a kapcsolatot a 2. fejezetben a feloldható bővítésekre alkalmazott Kummer-elmélettel. Ha a ([2]) sorozatban az ![]() bővítés helyére a
bővítés helyére a ![]() algebrai lezártat írjuk (és feltesszük, hogy
algebrai lezártat írjuk (és feltesszük, hogy ![]() -ban van primitív
-ban van primitív ![]() -edik egységgyök), akkor a
-edik egységgyök), akkor a ![]() -kohomológiák hosszú egzakt sorozata az
-kohomológiák hosszú egzakt sorozata az
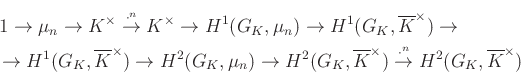
alakot ölti. Hilbert 90-es tételét újfent alkalmazva a ![]() csoport triviális, ezért
csoport triviális, ezért ![]() megegyezik a
megegyezik a ![]() Brauer-csoporton az
Brauer-csoporton az ![]() -edik hatványra emelés magjával, tehát az
-edik hatványra emelés magjával, tehát az ![]() -et osztó rendű elemek részcsoportjával. A Merkurjev-Szuszlin tétel pont ezekről szól: olyan centrális egyszerű algebrákról, melyek Brauer osztálya ebben a részcsoportban van. Tehát míg a
-et osztó rendű elemek részcsoportjával. A Merkurjev-Szuszlin tétel pont ezekről szól: olyan centrális egyszerű algebrákról, melyek Brauer osztálya ebben a részcsoportban van. Tehát míg a ![]() csoport explicit megadása viszonylag elemi, a
csoport explicit megadása viszonylag elemi, a ![]() leírásához a Merkurjev—Szuszlin tétel szükséges.
leírásához a Merkurjev—Szuszlin tétel szükséges.
5. Alkalmazások és kapcsolatok más területekkel
A Brauer-csoportnak létezik egy harmadik, geometriai interpretációja is. Vegyünk először egy ![]() kvaternióalgebrát a (
kvaternióalgebrát a (![]() -től különböző karakterisztikájú)
-től különböző karakterisztikájú) ![]() test fölött. Láttuk, hogy
test fölött. Láttuk, hogy ![]() felhasad (legalább) két másodfokú bővítés fölött: akár
felhasad (legalább) két másodfokú bővítés fölött: akár ![]() , akár
, akár ![]() négyzetgyökét elegendő adjungálni
négyzetgyökét elegendő adjungálni ![]() -hoz. Hogy lehetne ezt egy ennél uniformabb módon megfogalmazni? Tekintsük a
-hoz. Hogy lehetne ezt egy ennél uniformabb módon megfogalmazni? Tekintsük a ![]() projektív síkon a
projektív síkon a ![]() homogén koordinátákkal megadott görbét. Az alapvető észrevétel a következő:
homogén koordinátákkal megadott görbét. Az alapvető észrevétel a következő: ![]() -nek pontosan akkor van
-nek pontosan akkor van ![]() felett pontja (azaz
felett pontja (azaz ![]() ), ha az
), ha az ![]() centrális egyszerű algebra
centrális egyszerű algebra ![]() -val izomorf. Sőt, ha
-val izomorf. Sőt, ha ![]() egy tetszőleges bővítése
egy tetszőleges bővítése ![]() -nak, akkor
-nak, akkor ![]() ekvivalens azzal, hogy
ekvivalens azzal, hogy ![]() felhasítja
felhasítja ![]() -t. Továbbá algebrailag zárt test fölött
-t. Továbbá algebrailag zárt test fölött ![]() a
a ![]() projektív egyenessel izomorf. Általában Severi—Brauer-varietásnak nevezzük az
projektív egyenessel izomorf. Általában Severi—Brauer-varietásnak nevezzük az ![]() algebrai varietást a
algebrai varietást a ![]() test fölött, ha
test fölött, ha ![]() valamilyen
valamilyen ![]() -re az
-re az ![]() -dimenziós projektív tér egy csavart formája, azaz
-dimenziós projektív tér egy csavart formája, azaz ![]() . Mivel
. Mivel ![]() automorfizmuscsoportja
automorfizmuscsoportja ![]() — akárcsak
— akárcsak ![]() -nak —, ezért az
-nak —, ezért az ![]() -dimenziós Severi—Brauer-varietásokat ugyanaz a kohomológiacsoport klasszifikálja, mint az
-dimenziós Severi—Brauer-varietásokat ugyanaz a kohomológiacsoport klasszifikálja, mint az ![]() -edfokú centrális egyszerű algebrákat. Ez az észrevétel rendkívül fontos szerepet játszik a Merkurjev—Szuszlin-tétel bizonyításában, és általában a centrális egyszerű algebrák elméletében, hiszen ezen keresztül geometriai módszerek is alkalmazhatók.
-edfokú centrális egyszerű algebrákat. Ez az észrevétel rendkívül fontos szerepet játszik a Merkurjev—Szuszlin-tétel bizonyításában, és általában a centrális egyszerű algebrák elméletében, hiszen ezen keresztül geometriai módszerek is alkalmazhatók.
A Brauer-csoport alapvető fontosságú az algebrai számelméletben is, azon belül az osztálytestelméletben. Az osztálytestelmélet fő célja általános reciprocitási tételek igazolása. Ezen kapcsolat megértéséhez vegyünk ![]() felett egy
felett egy ![]() kvaternióalgebrát. Ez pontosan akkor hasad, ha
kvaternióalgebrát. Ez pontosan akkor hasad, ha ![]() . Mivel ez egy homogén másodfokú egyenlet, alkalmazhatjuk a Hasse—Minkowski-tételt, mely szerint a
. Mivel ez egy homogén másodfokú egyenlet, alkalmazhatjuk a Hasse—Minkowski-tételt, mely szerint a ![]() pontosan akkor, ha
pontosan akkor, ha ![]() , és minden
, és minden ![]() prímszámra
prímszámra ![]() . Másszóval az
. Másszóval az ![]() kvaternióalgebra pontosan akkor hasad
kvaternióalgebra pontosan akkor hasad ![]() fölött, ha hasad
fölött, ha hasad ![]() fölött minden
fölött minden ![]() -re (beleértve az
-re (beleértve az ![]() -t is, melyre
-t is, melyre ![]() ). Utóbbi nemcsak kvaternióalgebrákra igaz, hanem tetszőleges centrális egyszerű algebrára: tehát ez esetben teljesül a Hasse-féle lokális—globális elv. A kohomológiacsoportok nyelvén ez annyit tesz, hogy a
). Utóbbi nemcsak kvaternióalgebrákra igaz, hanem tetszőleges centrális egyszerű algebrára: tehát ez esetben teljesül a Hasse-féle lokális—globális elv. A kohomológiacsoportok nyelvén ez annyit tesz, hogy a
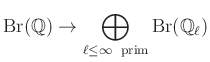
természetes leképezés injektív. Ahhoz, hogy ![]() képét megértsük, meg kell határoznunk először a lokális testek Brauer-csoportját. Megmutatható8, hogy amennyiben
képét megértsük, meg kell határoznunk először a lokális testek Brauer-csoportját. Megmutatható8, hogy amennyiben ![]() véges, akkor
véges, akkor ![]() , illetve az
, illetve az ![]() esetben
esetben ![]() másodrendű ciklikus csoport9. Ez az azonosítás kanonikus (nem függ semmilyen választástól): adott
másodrendű ciklikus csoport9. Ez az azonosítás kanonikus (nem függ semmilyen választástól): adott ![]() feletti centrális egyszerű algebrához tartozó
feletti centrális egyszerű algebrához tartozó ![]() -beli elemet az algebra Hasse-invariánsának nevezünk. Továbbá vegyünk minden
-beli elemet az algebra Hasse-invariánsának nevezünk. Továbbá vegyünk minden ![]() prímre egy
prímre egy ![]() -beli (és
-beli (és ![]() -re egy
-re egy ![]() -beli) elemet úgy, hogy véges sok kivétellel mindegyik 0 legyen. Pontosan akkor létezik olyan
-beli) elemet úgy, hogy véges sok kivétellel mindegyik 0 legyen. Pontosan akkor létezik olyan ![]() feletti centrális egyszerű algebra, melynek lokális Hasse-invariánsai az
feletti centrális egyszerű algebra, melynek lokális Hasse-invariánsai az ![]() számok, ha ezen számok összege 0. Másszóval a
számok, ha ezen számok összege 0. Másszóval a
sorozat egzakt. Ez hasonló mélységű eredmény, mint maga az osztálytest-elmélet: a ![]() véges bővítéseire vonatkozó általánosításaiból következnek a főbb reciprocitási tételek. Ennek illusztrálásaként megmutatjuk a Gauss-féle kvadratikus reciprocitási tételt. Mivel
véges bővítéseire vonatkozó általánosításaiból következnek a főbb reciprocitási tételek. Ennek illusztrálásaként megmutatjuk a Gauss-féle kvadratikus reciprocitási tételt. Mivel ![]() -ben egyetlen másodrendű elem van (jelesül az
-ben egyetlen másodrendű elem van (jelesül az ![]() mellékosztálya), a Brauer-csoport
mellékosztálya), a Brauer-csoport ![]() -torziójában minden esetben egyetlen nemtriviális elem van lokálisan, mégpedig
-torziójában minden esetben egyetlen nemtriviális elem van lokálisan, mégpedig ![]() esetén
esetén ![]() , páratlan
, páratlan ![]() esetén az
esetén az ![]() kvaternióalgebra, ahol
kvaternióalgebra, ahol ![]() kvadratikus nemmaradék modulo
kvadratikus nemmaradék modulo ![]() ,
, ![]() esetén pedig (ugyancsak) a
esetén pedig (ugyancsak) a ![]() kvaternióalgebra osztálya.10 Tehát a ([4]) sorozat egzaktsága a
kvaternióalgebra osztálya.10 Tehát a ([4]) sorozat egzaktsága a ![]() -torzióra nézve azt jelenti, hogy minden
-torzióra nézve azt jelenti, hogy minden ![]() feletti kvaternióalgebra páros sok
feletti kvaternióalgebra páros sok ![]() esetén nem hasad lokálisan
esetén nem hasad lokálisan ![]() -nél (hiszen páros sok
-nél (hiszen páros sok ![]() összege van
összege van ![]() -ben, páratlan soké nem). Namármost, ha
-ben, páratlan soké nem). Namármost, ha ![]() páratlan prímek, akkor a
páratlan prímek, akkor a ![]() kvaternióalgebra hasad
kvaternióalgebra hasad ![]() felett (hiszen
felett (hiszen ![]() és
és ![]() pozitívak), és minden
pozitívak), és minden ![]()
![]() -től és
-től és ![]() -tól különböző prímre
-tól különböző prímre ![]() felett is.11 Továbbá
felett is.11 Továbbá ![]() (ill.
(ill. ![]() ) fölött pontosan akkor hasad
) fölött pontosan akkor hasad ![]() , ha
, ha ![]() (ill.
(ill. ![]() ) kvadratikus maradék
) kvadratikus maradék ![]() (ill.
(ill. ![]() ), azaz ha
), azaz ha 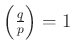 (ill. ha
(ill. ha 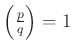 ).
). ![]() fölött pedig pontosan akkor hasad, ha
fölött pedig pontosan akkor hasad, ha ![]() nem teljesül, azaz ha
nem teljesül, azaz ha ![]() . Ezt összegezve adódik a jól ismert
. Ezt összegezve adódik a jól ismert
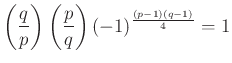
kvadratikus reciprocitási tétel.
Nem meglepő, hogy ha a Brauer-csoport ![]() -torziója helyett
-torziója helyett ![]() -torzióját vizsgáljuk, magasabb fokú reciprocitási tételeket kapunk: Legyen most
-torzióját vizsgáljuk, magasabb fokú reciprocitási tételeket kapunk: Legyen most ![]() tetszőleges test, mely valamely
tetszőleges test, mely valamely ![]() -re tartalmaz egy
-re tartalmaz egy ![]() primitív
primitív ![]() -edik egységgyököt. Az
-edik egységgyököt. Az ![]() ciklikus algebra Hasse-invariánsa
ciklikus algebra Hasse-invariánsa ![]() -edrendű elem
-edrendű elem ![]() -ben. Ez megad egy
-ben. Ez megad egy
alternáló bilineáris leképezést. Ráadásul az ![]() ún. Galois-szimbólum értéke pontosan akkor
ún. Galois-szimbólum értéke pontosan akkor ![]() , ha az
, ha az ![]() ciklikus algebra hasad. Ezt az
ciklikus algebra hasad. Ezt az ![]() elemekre lefordítva azt kapjuk, hogy
elemekre lefordítva azt kapjuk, hogy ![]() pontosan akkor áll elő normaként a
pontosan akkor áll elő normaként a ![]() bővítésben, ha
bővítésben, ha ![]() előáll normaként a
előáll normaként a ![]() bővítésben — ez is egy reciprocitási tétel. Amennyiben
bővítésben — ez is egy reciprocitási tétel. Amennyiben ![]() az
az ![]() -adikus számok
-adikus számok ![]() testének egy véges bővítése (azaz egy nemarkhimédészi lokális test), akkor ennél többet is mondhatunk, mert a
testének egy véges bővítése (azaz egy nemarkhimédészi lokális test), akkor ennél többet is mondhatunk, mert a ![]() csoportot azonosíthatjuk az
csoportot azonosíthatjuk az ![]() ciklikus csoporttal. Ez esetben az ([5]) bilineáris forma nemelfajuló, melyet Hilbert-szimbólumnak neveznek. Vegyük észre, hogy ([5]) függ
ciklikus csoporttal. Ez esetben az ([5]) bilineáris forma nemelfajuló, melyet Hilbert-szimbólumnak neveznek. Vegyük észre, hogy ([5]) függ ![]() választásától, viszont ha
választásától, viszont ha ![]() -t azonosítjuk
-t azonosítjuk ![]() -nel úgy, hogy
-nel úgy, hogy ![]() -et
-et ![]() -ba küldjük, akkor
-ba küldjük, akkor ![]() -értékű bilineáris leképezésként már lokális testek esetén a Hilbert-szimbólum nem függ semmilyen választástól.
-értékű bilineáris leképezésként már lokális testek esetén a Hilbert-szimbólum nem függ semmilyen választástól.
A Merkurjev—Szuszlin-tételt ebben a kontextusban úgy is megfogalmazhatjuk, hogy az ([5]) bilineáris leképezés képtere generálja ![]() -et, hiszen a képtér elemei éppen a ciklikus algebrák Brauer-osztályai, az összeadás a kohomológiacsoporton pedig az algebrák tenzorszorzatának felel meg. Vagy még elegánsabban: ([5]) indukál egy
-et, hiszen a képtér elemei éppen a ciklikus algebrák Brauer-osztályai, az összeadás a kohomológiacsoporton pedig az algebrák tenzorszorzatának felel meg. Vagy még elegánsabban: ([5]) indukál egy
![]()
csoporthomomorfizmust, és a Merkurjev—Szuszlin-tétel állítása nem más, mint ![]() szürjektivitása. Ennek messzemenő általánosítása az ún. motivikus Bloch—Kato-sejtés (Vojevodszkij12 tétele a 2000-es évekből), mely szerint az analóg
szürjektivitása. Ennek messzemenő általánosítása az ún. motivikus Bloch—Kato-sejtés (Vojevodszkij12 tétele a 2000-es évekből), mely szerint az analóg
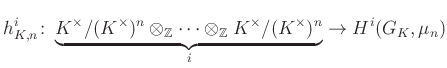
leképezés szürjektív minden ![]() -re és
-re és ![]() -re. Vojevodszkij már korábban, 2002-ben megkapta az egyik legnagyobb matematikai elismerésnek számító Fields-érmet a Milnor-sejtés bizonyításáért, mely az
-re. Vojevodszkij már korábban, 2002-ben megkapta az egyik legnagyobb matematikai elismerésnek számító Fields-érmet a Milnor-sejtés bizonyításáért, mely az ![]() speciális esete a Bloch—Kato-sejtésnek. Vojevodszkij ezekhez a Merkurjev—Szuszlin-tétel (mely az
speciális esete a Bloch—Kato-sejtésnek. Vojevodszkij ezekhez a Merkurjev—Szuszlin-tétel (mely az ![]() eset) igazolásához szükséges technikákat is használ, az általa kifejlesztett „motivikus” módszereken kívül.
eset) igazolásához szükséges technikákat is használ, az általa kifejlesztett „motivikus” módszereken kívül.
Zábrádi Gergely
Zábrádi Gergely az ELTE-n végzett 2005-ben, Cambridge-ben doktorált matematikából John Coates témavezetésével. Posztdoktorként Németországban volt, 2010 óta adjunktus az ELTE Algebra és Számelmélet tanszékén. 2018-ban Gács András díjat kapott.
Lábjegyzetek
- 1A tenzorszorzatot úgy képzelhetjük el, mint a bilineáris leképezések klasszifikáló terét: ez
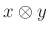 alakú elemi tenzorok formális lineáris kombinációiból áll, melyek a szokásos „bilinearitási” relációkat teljesítik. Ha mindkét szorzandó
alakú elemi tenzorok formális lineáris kombinációiból áll, melyek a szokásos „bilinearitási” relációkat teljesítik. Ha mindkét szorzandó 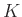 -algebra, akkor a tenzorszorzat is az lesz: egy
-algebra, akkor a tenzorszorzat is az lesz: egy 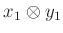 és egy
és egy 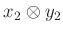 elemi tenzor szorzata az
elemi tenzor szorzata az 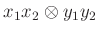 elemi tenzor lesz.
elemi tenzor lesz. - 2 Tehát az
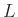 test azon automorfizmusainak (önmagával való művelettartó bijekcióinak) a csoportja, melyek
test azon automorfizmusainak (önmagával való művelettartó bijekcióinak) a csoportja, melyek 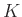 elemeit pontonként fixálják.
elemeit pontonként fixálják. - 3 Egy (Abel) csoportokból álló sorozatot egzaktnak hívunk, ha bármely két egymást követő homomorfizmus esetén az első képe megegyezik a második magjával. Pl. az
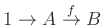 sorozat pontosan akkor egzakt, ha
sorozat pontosan akkor egzakt, ha 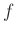 injektív.
injektív. - 4 Lásd akár itt: https://en.wikipedia.org/wiki/Hilbert's_Theorem_90.
- 5 Itt
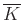 az algebrai lezártat jelöli, és feltesszük, hogy a
az algebrai lezártat jelöli, és feltesszük, hogy a 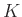 test tökéletes. Ha
test tökéletes. Ha 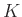 nem tökéletes, akkor az algebrai lezárt helyett a
nem tökéletes, akkor az algebrai lezárt helyett a 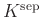 szeparábilis lezártat kell venni.
szeparábilis lezártat kell venni. - 6 Az injektivitás Hilbert
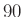 -es tétele
-es tétele 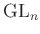 -re, miszerint
-re, miszerint 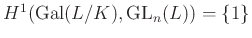 . Persze ehhez be kell azt is látni, hogy
. Persze ehhez be kell azt is látni, hogy 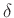 csoporthomomorfizmus a
csoporthomomorfizmus a 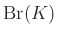 -ból örökölt csoportstruktúrában, hiszen enélkül a mag trivialitásából még nem következne az injektivitás. A szürjektivitáshoz viszont dolgozni kell.
-ból örökölt csoportstruktúrában, hiszen enélkül a mag trivialitásából még nem következne az injektivitás. A szürjektivitáshoz viszont dolgozni kell. - 7 A. S. Merkurjev, A. A. Suslin: K-Cohomology of Severi-Brauer varieties and the norm residue homomorphism, Izvestiya: Mathematics 21.2 (1983): 307—340.
- 8 Létezik tisztán kohomologikus érvelés is, de az egyik legelegánsabb bizonyítás centrális egyszerű algebrákon keresztül adható: a kulcs annak igazolása, hogy minden centrális egyszerű algebra felhasad egy alkalmas — az algebrától függő — elágazásmentes bővítés fölött.
- 9 Ez nem más, mint Frobenius tétele, mely szerint
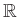 -en,
-en, 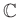 -n és
-n és 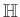 -n kívül nincs további nullosztómentes végesdimenziós
-n kívül nincs további nullosztómentes végesdimenziós 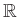 -algebra. Itt
-algebra. Itt 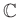 -nek a centruma nem
-nek a centruma nem 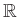 , ezért a Brauer-csoportban az egyetlen nemtriviális elem
, ezért a Brauer-csoportban az egyetlen nemtriviális elem 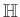 osztálya.
osztálya. - 10 Ezen kvaternióalgebrák valóban nem hasadnak, ugyanis ha
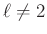 prím, akkor az
prím, akkor az 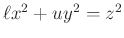 egyenletnek már modulo
egyenletnek már modulo 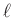 sincs nemtriviális megoldása, ill. az
sincs nemtriviális megoldása, ill. az 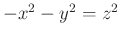 egyenletnek nincs
egyenletnek nincs 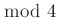 nemtriviális megoldása.
nemtriviális megoldása. - 11 Ugyanis
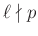 és
és 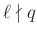 miatt modulo
miatt modulo 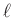 pontosan
pontosan 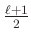 darab elem áll elő
darab elem áll elő 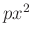 alakban és
alakban és 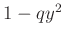 alakban is, ezért ezen két halmaznak van egy nemüres metszete modulo
alakban is, ezért ezen két halmaznak van egy nemüres metszete modulo 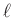 , azaz van olyan
, azaz van olyan 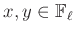 , melyre
, melyre 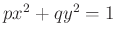 . Ezt a modulo
. Ezt a modulo 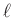 megoldást pedig a Hensel-lemma miatt fel lehet emelni egy
megoldást pedig a Hensel-lemma miatt fel lehet emelni egy 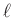 -adikus megoldássá, ha
-adikus megoldássá, ha 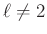 .
. - 12 azaz angol írásmóddal Voevodsky, 2017 őszén fiatalon elhunyt orosz/amerikai matematikus
- 13 Ezt a leképezést valójában a kohomológiákon való csészeszorzás indukálja, mivel
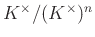 azonosítható
azonosítható 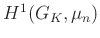 -nel. Amennyiben
-nel. Amennyiben 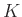 nem tartalmaz primitív
nem tartalmaz primitív 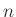 -edik egységgyököt (de karakterisztikája nem osztja
-edik egységgyököt (de karakterisztikája nem osztja 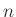 -et), akkor a jobb oldalon
-et), akkor a jobb oldalon 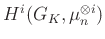 -t kell venni
-t kell venni 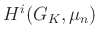 helyett.
helyett.