Történt egyszer, a városi legenda szerint, hogy Esterházy Péter a megjelenése után erősen dicsérte Raymond Smullyan, Gödel nemteljességi tételei című könyvét,[1] amit ugyanúgy Csaba Ferenc fordított, mint Torkel Franzén azonos című (de más alcímű) kötetét. Fel is töltötték Smullyan munkájával az Írók Boltjának polcait, és a kötet abban az évben a literátus emberek sokaságának került a birtokába. Pedig Smullyan könyve néhány rövid szakaszt leszámítva szinte csak matematikusok számára fogyasztható, szemben Franzénével, hiszen ez utóbbi kötet minden érdeklődő számára szánt érthető olvasmány. Főként arról szól ez a tanulmány, hogy Gödel első és második nemteljességi tételének a népszerűsítő irodalomban szereplő interpretációi milyen értelemben tekinthetők helyesnek vagy hol váltanak át parttalan fantáziálásba, elfeledkezve arról, hogy ezek a tételek mindenféle interpretáció nélkül, önmagukban is érdekes állításokat tesznek a matematikáról.[2]
Torkel Franzén (1950–2006) már nincs köztünk. A nemteljességről írott könyve megjelenésének évében daganatos betegséget diagnosztizáltak nála, és néhány hónap múlva elhunyt, betölthetetlen űrt hagyva a matematikafilozófiát művelők világában. A Luleåi Műszaki Egyetemen, a Számítógép-tudományi Tanszéken dolgozott és a Stockolmi Egyetemen doktorált [7]. Franzénról nem lehet beszélni anélkül, hogy ne beszélnénk Dag Prawitzról (1936–) és Prawitzról pedig nem lehet beszélni, anélkül, hogy ne beszélnénk Gerhard Gentzenről (1909–1945), ezért néhány szóban bemutatjuk azt a logikafilozófiai közeget, amelyben ők alapvető szerepet játszanak.

Torkel Franzén 2004-ben, Örnvikben egy konferencián
Gentzen, szemben a matematikai logikában ma is szokásos móddal, amely sok axiómával és kevés levezetési szabállyal dolgozik, olyan rendszert javasolt, amelyben sok a levezetési szabály, és nincsenek (logikai) axiómák. Az ilyen rendszereket természetes levezetési rendszereknek nevezzük. Az elnevezés indoka a következő egyszerű gondolaton alapul. A logikai konnektívumokhoz (,,és”, ,,vagy”, ,,ha, ... akkor, …”, ...) bevezetési és kiküszöbölési szabályokat rendel. A bevezetési szabályok olyanok, amelyek azt mondják meg, hogy egy logikai konnektívumot tartalmazó mondatra milyen körülmények között lehet következtetni. A kiküszöbölési szabályok pedig azt mondják meg, hogy ha egy mondatban egy logikai konnektívum szerepel, akkor ebből milyen következtetéseket lehet levonni. Például a legegyszerűbb: A és B együttes állítása alapot ad arra, hogy következtethessünk A&B-re (ez az &, azaz az ,,és” bevezetési szabálya); A&B állítása alapot ad arra, hogy akár A-ra, akár B-re következtethessünk. Hozzávetőlegesen ilyen egyszerűek, ilyen természetesek a természetes levezetési rendszer szabályai. Vegyük észre, hogy amikor az imént az ,,és” értelméről beszéltünk, akkor nem beszéltünk semmilyen értelemben az ,,igaz” illetve ,,hamis” értékről. Mi több, az ,,axióma” kifejezést sem használtuk. Ezeknek a szemantikai fogalmaknak mindenfajta használatát Gentzen elkerülte.

Dag Prawitz
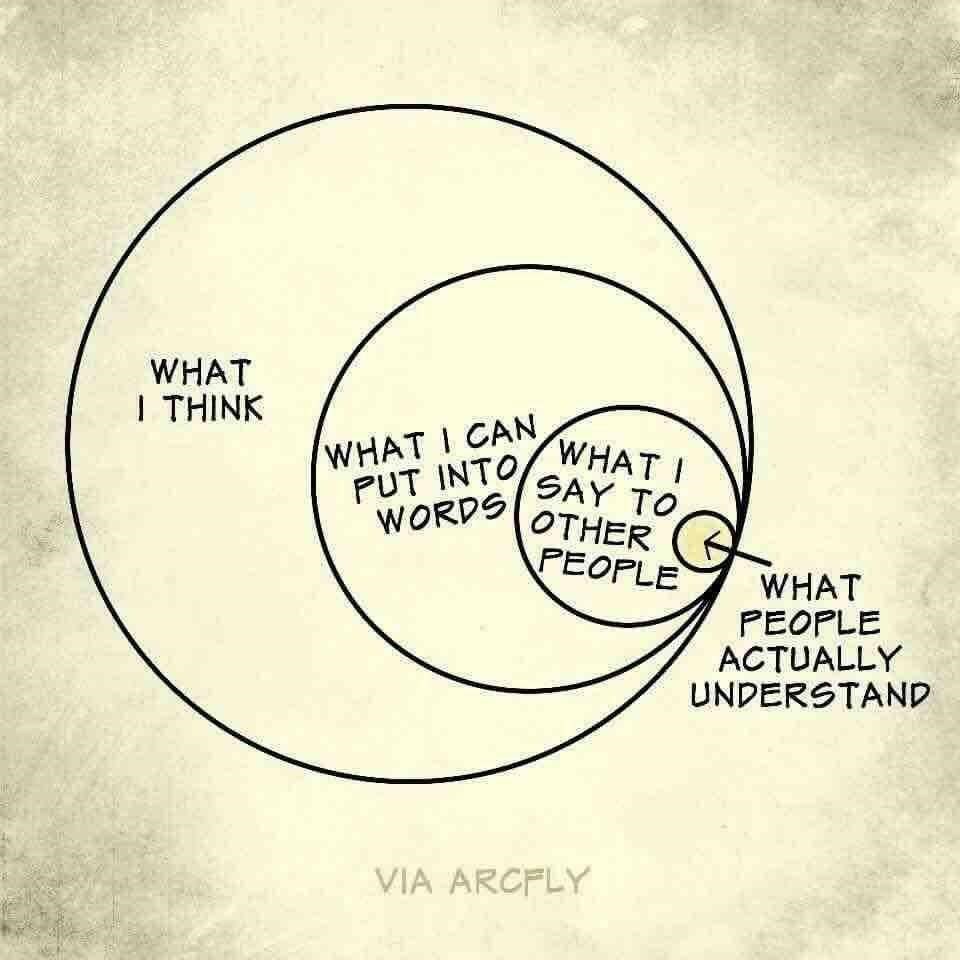
Prawitz Gentzennek egyetlen félmondatát helyezte a vizsgálódásai középpontjába: ,,a bevezetési szabályok igazolják a kiküszöbölési szabályokat”. Ha ugyanis abban a helyzetben vagyunk, hogy állíthatjuk A&B-t, akkor ez csak úgy lehetett, ha magát A-t és B-t is állítottuk, azaz a kiküszöbölési szabályra egyáltalán nincs szükség. Az a tény, hogy a logika következtetési szabályai között ilyen mélyebb kapcsolat állhat fenn, szöget ütött Prawitz fejében. A levezetés, a bizonyítás a matematikai megismerés folyamatában lényegesebb és világosabb szerepet játszik, mint az, hogy egy matematikai állítás ,,igaz”. A matematika érvényes állításainak elkülönítésében és értelmük feltárásában a levezetés játszik alapvető jelentéselméleti szerepet, konkrétan pedig Prawitz arra az álláspontra helyezkedett, hogy a matematika jelentéselmélete rokonítható az analitikus nyelvfilozófiában használatelméletnek nevezett állásponttal. Gentzen félmondatán elgondolkodva Prawitz még arra is megkísérelt választ adni, hogy milyen jellegzetességekkel bír a matematikai nyelvnek ez a használatelméleti szemantikája. A matematikai kifejezések jelentése csak olyasmi lehet, amit kommunikálni lehet. Amit nem lehet megfogalmazni, közös és általános tudományos diskurzus tárgyává tenni, az nem lehet a jelentés része. Nincs értelme azon jelentésrészeknek, amelyekről ugyan az egyes szereplők külön meg vannak győződve, de nem tudnak beszélni róla. Jól ábrázolja ezt a jelenséget az alábbi mém: eszerint a szociálkonstruktivista felfogás szerint a legbelső pici körben lévő szakmai kommunikációra alkalmas mondanivaló az, ami a voltaképpeni (objektív) matematikát alkotná [6].
Hogyan érhető tetten ez a szemlélet Franzénnál? Franzén doktori témavezetője Prawitz volt, és mindenestül magáévá tette azt a személetet, mely képes elrugaszkodni nem csak az ,,igaz” és ,,hamis” használatától, de még a halmazelmélettől is. Képes tehát arra is, hogy a gyakorló matematikusok között általános halmazelméleti realizmusnak nevezett világnézettől eltérő módon szemlélje a matematikát, például ne hivatkozzon a véges Neumann-rendszámok ω halmazára, mely végső soron nem más, mint amit a középiskolában a természetes számoknak neveztünk.[3] Ne feledjük el, hogy ezt mindenféle tudományos inkorrektség nélkül megteheti, mert a matematikáról való gondolkodásnak is megvannak a maga tudományos módszerei, amelyeket éppen olyanok fektettek le, akik maguk is kiváló matematikusok voltak, gondolok itt David Hilbertre, Alfred Tarskira, Neumann Jánosra vagy Kurt Gödelre. Nos, Franzén, amikor a Gödel-tétel félreértelmezéseiről beszél, nagyon alaposan részletezi és mindkét oldalról (a halmazelméleti realizmus és a használatelmélet szempontjából is) megvilágítja a tévedések okát és esetleges javíthatóságát. Ez mindenképpen olyan unikális eljárás, mely sok élvezetet fog okozni azoknak is, akik már találkoztak a témával. Ráadásul hű a Gödel-tételkör megalkotóihoz is, akik még képben voltak Hilbert és Gentzen informális matematikafelfogását illetően.
Ha az ember figyelmesen olvassa a könyvet, akkor arra a következtetésre juthat, hogy Franzén, amellett, hogy nagyon széles perspektívát nyújt a tétel értelmezéseiről, megfogalmaz egy matematikafilozófiai tézist is, és ezt a tanulmányában központi helyre pozicionálja. A következő meglepő állítást teszi a formális-axiomatikus számelméletre, azaz a Peano-aritmetikára (PA) vonatkozóan:
Másképpen: csupán a „PA konzisztens” és a „PA-ban bizonyítható az ikerprím sejtés” állítások alapján nem következtethetünk arra, hogy végtelen sok ikerprímpár létezik. (58. o.)
Illetve, amit többször is említ, és ami a (matematikai logikusok számára igen meglepő) tézise lenne:
A nemteljességi tétel konkrét példával szolgál olyan konzisztens elméletekre, amelyekben hamis állítások is bizonyíthatók. (42. o.)
Hangsúlyozom, hogy Franzén nem áll a halmazelméleti realizmus talaján, tehát ezen nem azt érti, hogy valamely számelméleti állítás nem igaz ω-ban, hanem hogy egy más értelemben nem igaz.[4] Itt valami olyanról beszél, ami a formális nyelvekkel kapcsolatos igazsághoz és bizonyításhoz köthető, de nem feltétlenül a halmazelmélethez. Először egy nagyon gyenge érvet fogok az állítása mellett felhozni, majd megpróbálok rámutatni arra, hogy Franzénnak, amennyiben fenntartja az állítását, miért kell mégis csak a halmazelméleti realizmust elfogadnia.
A gyenge (de legalább jó) próbálkozás Franzén tézisének igazolására a következő gondolatkísérlet. Először is a formális rendszerek formális állításai formális bizonyításainak létezése nem feltétlenül vonja maga után, hogy az állítás „a valóságban is igaz”. A legegyszerűbb példa a Ramsey-tétel egy véges változata, mely tulajdonképpen teljesen mindegy, hogy mit mond ki – a skatulyaelv egy általános verzióját –, a lényeg, hogy PA-ban megfogalmazható, de nem vezethető le belőle.[5] Azt a tényt, hogy a véges Ramsey-tétel ezen verziója (nevezzük VRT-nek) nem vezethető le PA-ból, Paris–Harrington-tételnek hívjuk, tehát ez egy matematikai logikai tétel [5]. A halmazelméletben (mondjuk ω elemeire) VRT bizonyítható. Most nem arra szeretném felhívni a figyelmet, hogy ez milyen érdekes, hanem a másik szemszögből közelíteném meg a problémát. Tegyük fel, hogy azok, akik kitalálták a PA-t, nem szándékozták a VRT-t igaznak tekinteni, mert mondjuk olyan bonyolultnak tartották, hogy nem hittek benne. Éppen ezért úgy alakították ki PA axiómarendszerét, hogy abból a VRT-t ne lehessen levezetni. Mivel nem hittek benne, nem is tartották igaznak. És valóban, VRT nem is levezethető PA-ból. Ám az a helyzet, hogy a VRT már az úgynevezett másodrendű aritmetikában, a PA2-ben is levezethető. PA2-ben beszélhetünk a természetes számok részhalmazainak konkrét halmazairól is, ami szintén olyan tevékenység, amit korábban nem feltétlenül szerettek volna a számokkal foglalkozók (gondolok itt Eukleidészre, vagy a skatulyaelvre utaló első szerzőre, Jean Leurechon jezsuita szerzetesre, esetleg magára Giuseppe Peanora), ezért nem meglepő, hogy egy olyan eredmény is kijött, melynek az igazsága eredetileg nem volt kívánatos. Ekkor tehát azt mondjuk, hogy ha PA2 ellentmondásmentes, akkor belőle egy nem szándékolt, hamis állítás is levezethető, ti. a VRT. Természetesen ez egy gondolatkísérlet. A feltevéssel szemben Eukleidészék semmit sem gondoltak a VRT-ről és a mai matematikusok azt gondolják, hogy a VRT bizonyítottan igaz. Elképzelhető azonban, hogy egy ilyen megtörténjen, tehát nem kizárt, hogy egy konzisztens formális rendszer ebben az értelemben vett hamis állítást bizonyítson.
Nagyon érdekes tehát, hogy Franzén nem mindig a halmazelméleti igazságra, hanem egy bővebb rendszerre, mondjuk a PA2-ra vagy más érdekesebb elméletekre hivatkozik. S mivel ezt rendkívül olvasmányosan teszi, ezért ezek a gondolatmenetek akár a matematikában csak középiskolai szinten járatos, akár a magasabb szinten tájékozott olvasónak örömére és tanulságául szolgálhat. Vannak azonban olyan részei a könyvnek, mely a matematikai logika területén erősen iskolázott olvasó számára is kihívást jelentenek, de ezek a részek nem gyakoriak, és főleg a fent említett – a matematikai igazsággal kapcsolatos – téziséhez kapcsolódnak.
Azt mondja ugyanis Franzén, hogy egy A formális matematikai állítás igaz, ha az, amit A állít (mond, kifejez, megfogalmaz), a valóságban is úgy van. Ezt nagyon helyesen Alfred Tarskira hivatkozva teszi, melyet Tarski-féle T-sémának nevezünk:
Alfred Tarski a múlt század 30-as éveiben mutatta meg, miként adható meg az igazság matematikai definíciója úgy, hogy az ,,A igaz” állítás ekvivalens legyen A-val. Tarski elméletét ebben a könyvben nem tárgyaljuk részletesen. (59. o.)
Nos, ez az utóbbi elég helytelen dolog, mert Tarski nem hallgatott el egy lényeges problémát [8]. Azt, hogy ez az elv ugyan sokszor megvalósítható, de konkrétan a formális-axiomatikus számelmélet esetén nem. Ott, a PA-ban, éppen az a helyzet, hogy van olyan A formális számelméleti kijelentés, melyet lefordítva természetes nyelvre (megnézzük mit mond valójában), a természetes nyelvi fordítása ekvivalens lesz azzal, hogy A hamis. Ez ugyanannak a jelenségnek a következménye, ami a Gödel-tételben is tapasztalható, csak nem a bizonyíthatóságra, hanem az igazságra vonatkozóan [4]. Természetesen vannak nagyon egyszerű formális állítások, melyeknek az igazsága problémamentes. Így például az 1+1=2 kijelentés pontosan akkor igaz, ha egy meg egy az kettő. De sokkal bonyolultabb állítások esetén a matematikai logikusoknak olyan tulajdonságokat kell megkövetelniük a számelmélet nyelvén felírt axiómarendszerekre vonatkozóan, amelyek legalább a formális állítások egy körére biztosítják, hogy ezeknek az igazsága ekvivalens legyen a természetes nyelvi fordításukkal. Az ilyen megszorítások azonban hivatkoznak ω-ra. Tehát vagy elfogadjuk a halmazelméleti realizmust vagy egyszerűen nem hivatkozunk az igazságra. Ezen kívül is vannak még megoldások, amelyekkel matematikafilozófusok éltek (akár David Hilbert [9], akár Michael Dummett [3]), de ezek a megoldások nem olyan egyszerűek, hogy egy olyan megnyugtató mondatba lehessen megfogalmazni, mint amilyen a Tarski-féle T-séma.[6] Sajnos ingatag lábakon álló téziséből messzemenő következtetéseket von le, például azt, hogy ellentmondásmentes elméletből hamis állítás is levezethető. Szerintem ez nem csak szokatlan, de hamis állítás is. Egy szó, mint száz, remélem, hogy az Olvasó is a Franzén és a köztem lévő nézetkülönbségben egy izgalmas diskurzus lehetőségét látja.
A könyvnek van egy nagyon figyelemre méltó része, mely a Gödel-tétel és az algoritmusok, a kiszámíthatóság kapcsolatát vizsgálja. Ezt együtt tárgyalja a Gödel-tétel és a diofantoszi egyenletek kapcsolatával, amely a középiskolai tudáshoz sokkal közelebb lévő fogalmakkal meséli el ezt a témakört. Ez a két átfogalmazás, a számítógépes interpretáció és a számelméleti egyenletek nyelvén elmondott történet azok számára is sokat mond, akik az egyetemen már találkoztak a Gödel-tételekkel, ritkaság ugyanis, hogy a matematikai logikai képzésben kitérnének arra, hogy milyen kapcsolat van a diofantikus egyenletek és a nemteljességi tételek között. Aki esetleg a könyv elejét magasabb matematikai műveltsége miatt unalmasnak találja, az is nagyon sok élvezetes és új gondolatmenetet találhat a kiszámíthatóságról szóló fejezetekben.
Csaba Ferenc fordítása szakmailag rendkívül megnyugtató. Régi jó ismerős ő logikai tárgyú könyvek és cikkek fordítása terén és nyelvhasználatban, szakmaiságban nem tud tévedni. Hogy csak egy alapvető tényt mondjak: A matematika filozófiája a XXI. század küszöbén c. gyűjteményes kötet, melynek ő a szerkesztője és a benne lévő cikkek közül néhánynak fordítója, elengedhetetlen a magyarországi matematikafilozófiai képzésben [1]. Két egyetem (a BME és az ELTE) egészen biztosan használja matematikafilozófiai népszerűsítő és professzionális kurzusain is. Összességében annak is örülhetünk, hogy Franzén könyve a kezünkbe kerülhet, de annak is, hogy ezt Csaba Ferenc kiváló fordításában olvashatjuk.
Torkel Franzén: Gödel nemteljességi tételei Értelmezések és félreértések, TypoTeX, 2013
Molnár Zoltán Gábor
Budapesti Műszaki és Gazdaságtudományi Egyetem
A közölt képek forrásai sorrendben:
http://www.sm.luth.se/csee/csn/Ornvik2004Photos/
https://yujiearthman.wordpress.com/2016/08/22/what-i-think-what-i-can-put-into-words-what-i-say-to-other-people-what-people-actually-understand/
Hivatkozások
[1] Csaba Ferenc, (szerk.), A matematika filozófiája a XXI. század küszöbén. Osiris, Bp. 2003.
[2] Raymond Smullyan, Gödel nemteljességi tételei, TYPOTeX, ford.: Csaba Ferenc, (1999), 2005
[3] Michael Dummett, The philosophical significance of Gödel’s theorem, Ratio 5, 140–155. (1963), Reprinted in M. Dummett: Truth and Other Enigmas, Duckworth, London, 1978, 186–201., p. 186.
[4] Gödel, Kurt, On Formally Undecidable Propositions of Principia Mathematica and Related Systems, in From Frege to Gödel: A Source Book in Mathematical Logic, 1879–1931, ed.: Jean Van Heijenoort, Harvard University Press, 1967
[5] Paris, J. and Harrington, L. A Mathematical Incompleteness in Peano Arithmetic. In Jon Barwise (ed.), Handbook of Mathematical Logic (Studies in Logic and the Foundations of Mathematics), North-Holland; New edition 1982
[6] Dag Prawitz, Jelentés és bizonyítás: a klasszikus és intuicionista logika konfliktusa in [1]
[7] Solomon Feferman nekrológja a FOM (Foundations of Mathematics) levelezési listán: http://www.cs.nyu.edu/pipermail/fom/2006-April/010463.html
[8] Alfred Tarski, Az igazság fogalma a formalizált nyelvekben, in: Ruzsa I. (szerk.), A. Tarski – Bizonyítás és igazság, Gondolat, 1989
[9] Zach, Richard, The Practice of Finitism: Epsilon Calculus and ConsistencyProofs in Hilbert's Program, Synthese, 137:211-259, 2001.
Lábjegyzetek
[1] Raymond Smullyan, Gödel nemteljességi tételei, TYPOTeX, ford.: Csaba Ferenc, (1999), 2005 http://www.typotex.hu/book/196/raymond_smullyan_godel_nemteljessegi_tetelei
[2]Gödel első nemteljességi tétele azt mondja, ki, hogy a formális-axiomatikus számelmélet minden ellentmondásmentes, az emberi elme által áttekinthető axiómákkal történő bővítése olyan, hogy abban megfogalmazható egy olyan számelméleti állítás, amely se nem bizonyítható, se nem cáfolható az axiómák alapján. A második tétel pedig azt mondja ki, hogy ugyanebben az axiómarendszerben az axiómarendszer ellentmondás-mentességét megfogalmazó számelméleti állítás nem bizonyítható.
[3]Szűk értelemben véve, azaz a számelmélet kontextusában a halmazelméleti realizmus olyasmit jelent, hogy a számokat azonosítjuk a véges Neumann-rendszámokkal. A szokásos halmazelméleti felépítésben az üres halmaz felel meg a 0-nak, az üres halmazt tartalmazó egyelemű halmaz az 1-nek, ez utóbbi kettőt tartalmazó kételemű halmaznak a 2, és így tovább. Ezeknek a halmazoknak a halmazát nevezzük a véges Neumann-rendszámok halmazának és ω-val (omegával) jelöljük.
[4] Lásd a 3. lábjegyzetet.
[5] A véges Ramsey-tétel ezen verziója a következő. Minden pozitív egész n, k>1 ill. m>n-1 számhoz található olyan N pozitív egész szám, hogy ha kiszínezzük a H = {1, 2, 3,..., N} halmaz összes n-elemű részhalmazát k színnel, akkor lesz H-nak olyan K részhalmaza, mely legalább m elemet fog tartalmazni úgy, hogy K-nak minden n-elemű részhalmaza azonos színből fog állni, és K elemeinek száma legalább annyi, mint K elemei közül a legkisebb.
[6] Franzén a gondolatmenetében a 42. oldalon elfeledkezik arról, hogy Tarski feltette, hogy amikor a természetes nyelvben megfogalmazunk egy matematikai elméletet, akkor ott ugyanazokat a matematikai axiómákat kell megkövetelnünk, mint amelyeket a formális elméletben posztuláltunk (különben a fordítás nyilvánvalóan elromlik). Amikor Franzén áttér egy új axiómarendszerre a ZFC +,,ZFC inkonzisztens”-re, akkor elfelejti az új axiómának megfelelő természetes nyelvi axiómát hozzávenni az eddigiekhez. Nehezíti még a problémát, hogy a fordítás ezen a helyen inkonzisztens helyett konzisztenst mond, ami elég erősen igénybe veszi az olvasó figyelmét. Hasonló elütések sajnos még néhány helyen találhatók a szövegben.









