„Geometriam more geometrico”

Életút és pályakép
Tamássy Lajos 1923. április 17-én született Debrecenben, és ugyanitt hunyt el 96. életévében, 2019. február 12-én. Szülei Bészler (1929-től Tamássy) Lajos vaskereskedő és Dömsödi Emma, aki tanítónői képesítéssel rendelkezett. A négyosztályos elemi iskola elvégzése után Pécsett, a Zrínyi Miklós Reáliskolában kezdte el középfokú tanulmányait. 1941-ben érettségizett, majd felvételt nyert a Ludovika Akadémiára. 1944 őszétől frontszolgálatot teljesített. Egy felderítési akció során megsebesült, a visszavonuló magyar sereg sérülten szállította magával. Végül, már Németországban, amerikai hadifogságba esett, amelyből 1945. májusában szabadult. 1946 tavaszán tért haza szülővárosába. Ez év őszén beiratkozott a Debreceni Tudományegyetem matematika-fizika-ábrázoló geometria szakára – akkoriban ehhez elegendő volt az érettségi bizonyítványt bemutatni. 1951-ben vette kézhez tanári diplomáját. Ezt követően rövid ideig a debreceni Gépipari Technikum tanára volt. 1952-ben a Szegedi Tudományegyetem Bolyai Intézetében kapott tanársegédi állást. Ugyanebben az évben, Debrecenben életre szóló házasságot kötött a kutatás és oktatás iránt ugyanúgy elkötelezett Lentei Ilonával. Ő a Kossuth Lajos Tudományegyetem (a későbbi Debreceni Egyetem) Elméleti Fizikai Tanszékén lett egyetemi tanár, majd (1981-től) a Fizikai Intézet első igazgatója. Házasságukból gyermek nem született. Az 1953-as év hozta meg az új és igazi kezdetet Tamássy Lajos pályafutásában: januárban kinevezést nyert a Kossuth Lajos Tudományegyetem Matematika Tanszékére. Végigjárta a teljes szolgálati utat: 1959-től adjunktus, 1964-től docens, 1975-től pedig egyetemi tanár. Közvetlenül nyugdíjba vonulása után, 1994-ben elnyerte a professor emeritus címet. Haláláig, tehát 66 éven át szolgálta példamutató odaadással az Egyetemet. Az előléptetések mindig a tudományos ranglétra magasabb fokára jutást követték. Tamássy Lajos 1958-ban lett egyetemi doktor, 1962-ben szerezte meg a kandidátusi, 1974-ben pedig a matematikai tudományok doktora fokozatot.
A Geometria Tanszék vezetését 1973-ban Rapcsák András akadémikustól vette át, és 15 éven át töltötte be ezt a pozíciót. Hatását tekintve, talán ez volt pályájának a legfontosabb szakasza. Átgondolt és következetesen végigvitt építkezés jellemzi ezeket az éveket mind a kutatási profil kor által megkövetelt modernizálásában (az értékes hagyományok megőrzése mellett), mind pedig a szükséges humánpolitikai lépések megtételében.
Jelentős energiát fordított arra, hogy ablakot nyisson a világra. 1976 nyarán főszervezője volt egy Debrecenben rendezett nagyszabású, magas színvonalú és rendkívül sikeres Differenciálgeometriai Kollokviumnak, amelyre szinte minden kontinensről érkeztek vezető kutatók. Ezt a konferenciát több hasonló is követte a Bolyai János Matematikai Társulat támogatásával.

A debreceni Geometria Tanszék 1979-ben: elöl ül Rapcsák András és Makoto Matsumoto, hátul állnak balról jobbra: Gyarmathi Attila, Kántor Sándorné, Szilasi József, Tamássy Lajos, Bácsó Sándor, Bélteky Károly, Varga József, Szabó József
Tamássy Lajos 1970-es években elért tudományos eredményei (amelyekről később kicsit bővebben szólunk) felkeltették a témában dolgozó és abban vezető szerepet játszó japán matematikusok érdeklődését. 1976 őszén több hónapra szóló vendégprofesszori meghívást kapott Japánba. Kint tartózkodása során a Kyotoi Egyetemen és a Japán Matematikai Társulat Tokiói Kongresszusán is tartott előadást. Viszonzásként Makoto Matsumoto, a Kyotoi Egyetem professzora töltött el 1979 januárjától négy hónapot intenzív munkával a debreceni Egyetemen. Heti két alkalommal tartott előadást a Geometria Tanszék oktatóinak a Finsler-geometria modern megalapozásáról, illetve speciális Finsler-sokaságokról, és Tamássy Lajossal közösen két dolgozatot is elkészített ([4], [5]). Ezzel a kölcsönös látogatással egy hosszan tartó és nagyon gyümölcsöző együttműködés indult meg a debreceni differenciálgeométerek és a Matsumoto professzor körül csoportosuló „Kyoto Group” kutatói között.

Tamássy Lajos Makoto Matsumotoval Japánban 1976-ban
Tamássy Lajos kezdettől fogva kiemelt feladatának tekintette egy kutatói utánpótlás kinevelését. Kilencen szereztek az irányításával kandidátusi, illetve – egyetemi doktori cím átminősítésével – PhD fokozatot. Tanítványai közül többen is a differenciálgeometria jeles kutatóivá váltak. Kimagasló iskolateremtő munkáját a Bolyai János Matematikai Társulat 1992-ben az általa adható legmagasabb kitüntetéssel, a Szele Tibor Emlékéremmel díjazta. Idézünk a laudációból:
„Tamássy Lajos egyik legkiemelkedőbb eredménye a Varga Ottó által alapított, majd később Rapcsák András által vezetett debreceni differenciálgeometriai iskola tovább vitele. Tamássy Lajosnak az utóbbi évtizedben sikerült a vezetése alatt dolgozó differenciálgeometriai kutatócsoport kutatásait a klasszikus lokális vizsgálatokról a modern globális vizsgálatokra átállítani. Tamássy Lajos érdeme, hogy a debreceni iskola megmaradt a magyarországi differenciálgeometriai kutatások nemzetközileg is elismert centrumának.”
Nyugdíjba vonulása után csak státusza változott, aktivitása nem. Naponta bejárt a Matematikai Intézetbe, részt vett annak életében. Vezette a doktori iskola „Differenciálgeometria és alkalmazásai” alprogramját. Egyetemi előadásokat tartott, kedvenc témáiban – még határozottabban a „more geometrico” szellemében – folytatta vizsgálódásait, és eredményeit rendszeresen publikálta. Jelentős külföldi konferenciákon adott elő meghívás alapján, így például 2010-ben, 87 évesen, Sanghajban a Chern Intézetben tartott plenáris előadást a síkprojektív terekről.
Még 1988-ban kinevezték a Publicationes Mathematicae (Debrecen) főszerkesztőjévé, és ezt a feladatkört haláláig ellátta. Fáradtságot nem ismerő, igényes és pontos szerkesztői munkájának köszönhetően ennek a korábban is komoly presztizzsel bíró folyóiratnak a rangja tovább emelkedett.

Tamássy Lajos munkásságát számos magas kitüntetéssel ismerték el. A Szele Tibor díjat már említettük. A továbbiak közül a legfontosabbak: Szent-Györgyi Albert-díj, a Magyar Köztársasági Érdemrend tisztikeresztje és középkeresztje; az MTA Eötvös József-koszorú díja. 2018-ban, 95 éves korában, elnyerte a Debreceni Egyetem Díszérme kitüntetést, amely az intézmény által adományozható legmagasabb elismerés.
Tenzornyaláboktól a távolság-terekig
Tamássy Lajos első munkái a tenzori összefüggések (a ma inkább használatos kifejezéssel: tenzori konnexiók) elméletéből születtek, és ehhez a témához pályája során többször is visszatért.
Egy sima sokaságon adott minden lineáris konnexió (amely szabadon interpretálható egy kovariáns deriválásnak nevezett differenciáloperátorként) kovariáns deriválást indukál a sokaság fölötti tenzornyalábokon. Megfordítva, megadva egy tenzornyalábon egy kovariáns deriválást (egy „tenzori konnexiót”), fölvethetjük a kérdést: milyen feltételek mellett és hogyan származtatható ez az alapsokaság egy lineáris konnexiójából? Ez az egyszerű (és elég könnyen megválaszolható) kérdés a tenzori konnexiók elméletének kiindulópontja. Az elmélet elindítója Enrico Bompiani volt egy 1946-ban megjelent rövid, olasz nyelvű dolgozatával. Vizsgálatai a 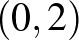 - és az
- és az 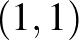 -típusú tenzorokra korlátozódtak, Tamássy Lajos kiterjesztette ezeket általános,
-típusú tenzorokra korlátozódtak, Tamássy Lajos kiterjesztette ezeket általános, 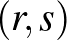 -típusú tenzorokra ([1]). A parciális differenciálegyenletek elméletéből ismert Thomas–Veblen eljárás segítségével meghatározta ugyanazon tenzornyalábon adott két tenzori konnexió ekvivalenciájának feltételét, és ezen az úton olyan tenzorinvariánsokat talált, amelyek a tenzori konnexiók görbületi tenzorainak, illetve torziótenzorának szerepét játsszák.
-típusú tenzorokra ([1]). A parciális differenciálegyenletek elméletéből ismert Thomas–Veblen eljárás segítségével meghatározta ugyanazon tenzornyalábon adott két tenzori konnexió ekvivalenciájának feltételét, és ezen az úton olyan tenzorinvariánsokat talált, amelyek a tenzori konnexiók görbületi tenzorainak, illetve torziótenzorának szerepét játsszák.
Utólag nézve, a tenzori konnexiók számos új eredményt hozó tanulmányozása valójában az előmunkálatokat jelentette az areal-terek még kevéssé feltárt és bonyolult világának a vizsgálatához. A következőkben először is röviden vázoljuk, hogy milyen motivációk vezettek az areal-terek bevezetéséhez, és megadjuk egy egyszerű, indexmentes definíciójukat.
Tekintsünk egy 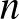 -dimenziós sima sokaságot, jelölje ezt
-dimenziós sima sokaságot, jelölje ezt  . Egy
. Egy  -en adott Riemann-féle metrikus tenzor („Riemann-metrika”, vagy egyszerűen „metrika”) a sokaság minden pontjának érintőterét felruházza egy euklideszi skaláris szorzattal, amely (euklideszi) normát indukál. Ez lehetővé teszi azt is, hogy az érintőterekben
-en adott Riemann-féle metrikus tenzor („Riemann-metrika”, vagy egyszerűen „metrika”) a sokaság minden pontjának érintőterét felruházza egy euklideszi skaláris szorzattal, amely (euklideszi) normát indukál. Ez lehetővé teszi azt is, hogy az érintőterekben 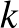 -dimenziós területmértéket („area measure”) vezessünk be, mégpedig egyértelműen, ha rögzítjük a
-dimenziós területmértéket („area measure”) vezessünk be, mégpedig egyértelműen, ha rögzítjük a 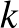 -dimenziós egységkocka mértékét.
-dimenziós egységkocka mértékét.
Élie Cartantól származik az a gondolat, hogy egy 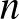 -dimenziós sokaságon adjunk meg olyan
-dimenziós sokaságon adjunk meg olyan 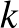 -dimenziós (
-dimenziós ( ) területmértéket, amelyet nem föltétlenül Riemann-metrika indukál, azaz építsünk fel egy olyan geometriát, amelyben van területmérték, de nincs a priori adott hosszmérték. Azt, hogy ez miként valósítható meg
) területmértéket, amelyet nem föltétlenül Riemann-metrika indukál, azaz építsünk fel egy olyan geometriát, amelyben van területmérték, de nincs a priori adott hosszmérték. Azt, hogy ez miként valósítható meg 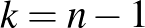 esetén, maga Cartan mutatta meg egy 1933-ban publikált könyvében ([B1]). Az általános eset kidolgozásához olyan jeles matematikusok járultak hozzá lényegesen, mint a japán Akitsugu Kawaguchi, a német Woldemar Barthel, a brit Evan Tom Davies és Frederick Brickell – s közéjük sorolható Tamássy Lajos is.
esetén, maga Cartan mutatta meg egy 1933-ban publikált könyvében ([B1]). Az általános eset kidolgozásához olyan jeles matematikusok járultak hozzá lényegesen, mint a japán Akitsugu Kawaguchi, a német Woldemar Barthel, a brit Evan Tom Davies és Frederick Brickell – s közéjük sorolható Tamássy Lajos is.
Az areal-terek definiálása céljából tekintsünk először egy 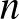 -dimenziós valós vektorteret, ahol
-dimenziós valós vektorteret, ahol 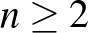 ; és legyen
; és legyen  . Egy lineárisan független vektorok alkotta
. Egy lineárisan független vektorok alkotta 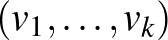 vektorsorozatról azt (is) mondjuk, hogy egy
vektorsorozatról azt (is) mondjuk, hogy egy 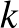 -él (
-él (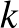 -frame)
-frame) 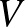 -ben. A
-ben. A 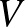 -beli
-beli 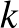 -élek halmazát
-élek halmazát 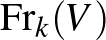 -vel jelöljük. Ez a halmaz rendelkezik egy természetes sima struktúrával, amellyel felruházva
-vel jelöljük. Ez a halmaz rendelkezik egy természetes sima struktúrával, amellyel felruházva 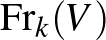
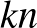 -dimenziós sokasággá válik, ez a
-dimenziós sokasággá válik, ez a 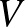 -beli
-beli 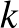 -élek alkotta Stiefel-sokaság. A
-élek alkotta Stiefel-sokaság. A 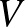 vektortéren adott
vektortéren adott 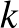 -dimenziós területmértéken olyan
-dimenziós területmértéken olyan
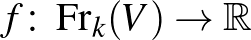
pozitív differenciálható függvényt értünk, amely rendelkezik a következő homogenitási tulajdonsággal:
ha 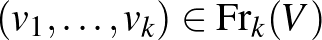 és
és 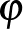 pozitív determinánsú lineáris izomorfizmusa
pozitív determinánsú lineáris izomorfizmusa 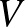 -nek, akkor
-nek, akkor 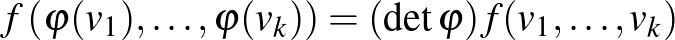 .
.
Ezen előkészületek után tekintsünk egy 
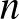 -dimenziós sokaságot (ahol
-dimenziós sokaságot (ahol 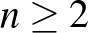 ), és képezzük az
), és képezzük az
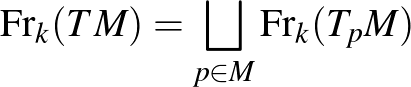
diszjunkt uniót. Ez a halmaz természetes módon sokaság-struktúrával ruházható fel. Ily módon 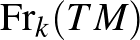 az
az  sokaság fölötti fibrált nyalábbá válik (egy
sokaság fölötti fibrált nyalábbá válik (egy 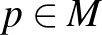 pont fölötti fibrum az
pont fölötti fibrum az 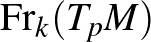 Stiefel-sokaság). Az
Stiefel-sokaság). Az  sokaságon adott
sokaságon adott 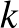 -dimenziós területmérték egy olyan
-dimenziós területmérték egy olyan
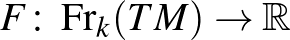
( 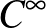 -) differenciálható függvény, amelyre az teljesül, hogy
-) differenciálható függvény, amelyre az teljesül, hogy 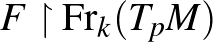
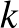 -dimenziós területmérték a
-dimenziós területmérték a 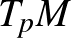 érintőtéren, minden
érintőtéren, minden 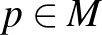 esetén. Ekkor azt mondjuk, hogy az
esetén. Ekkor azt mondjuk, hogy az 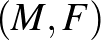 pár areal-tér
pár areal-tér 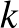 -dimenziós területmértékkel (röviden: areal-tér). Az
-dimenziós területmértékkel (röviden: areal-tér). Az 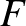 függvényt a tér alapfüggvényeként is említjük.
függvényt a tér alapfüggvényeként is említjük.
A legfontosabb speciális eset természetesen k=1 -re adódik.. Ekkor
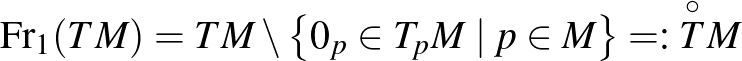
(ahol 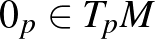 az érintőtér zérusvektora) és az alapfüggvényre kiszabott homogenitási feltétel azt adja, hogy
az érintőtér zérusvektora) és az alapfüggvényre kiszabott homogenitási feltétel azt adja, hogy 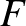 elsőfokú pozitív homogén, azaz
elsőfokú pozitív homogén, azaz
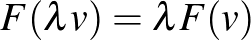
minden 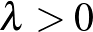 és
és 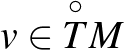 esetén. A területmérték hosszmértékké válik, és definiálható tetszőleges
esetén. A területmérték hosszmértékké válik, és definiálható tetszőleges ![$\gamma\colon [a,b]\rightarrow M$](/images/stories/latexuj/2023-05/2023-05-tamassylajos/img34.png) reguláris differenciálható görbe
reguláris differenciálható görbe
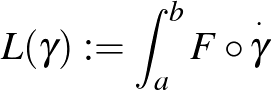
ívhossza (ahol ![$\overset{\cdot}{\gamma}\colon [a,b]\rightarrow\overset{\circ}{T}M$](/images/stories/latexuj/2023-05/2023-05-tamassylajos/img36.png) a görbe sebességvektormezője). Ha az
a görbe sebességvektormezője). Ha az 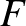 függvényt kiterjesztjük
függvényt kiterjesztjük 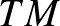 -re, előírva, hogy zérusvektorban nullát vegyen fel, és megkívánjuk az alább megfogalmazásra kerülő (K) konvexitási feltétel teljesülését, akkor Finsler-alapfüggvényről vagy Finsler-függvényről beszélünk, s a Finsler-geometria világába jutunk.
-re, előírva, hogy zérusvektorban nullát vegyen fel, és megkívánjuk az alább megfogalmazásra kerülő (K) konvexitási feltétel teljesülését, akkor Finsler-alapfüggvényről vagy Finsler-függvényről beszélünk, s a Finsler-geometria világába jutunk.
(K) Tetszőleges 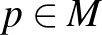 pont és
pont és 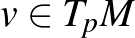 nemzérus érintővektor esetén a
nemzérus érintővektor esetén a
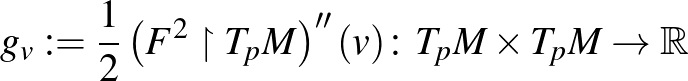
szimmetrikus bilineáris forma pozitív definit.
A 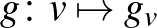 leképezés a Finsler-sokaság metrikus tenzora. Ez alkalmas hosszmérésre, ugyanis
leképezés a Finsler-sokaság metrikus tenzora. Ez alkalmas hosszmérésre, ugyanis
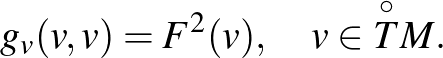
Térjünk vissza az általános
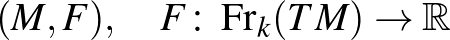
areal-terekhez! Elméletük kiépítése során az első komoly nehézséget egy olyan metrikus tenzor bevezetése jelentette, amelyből a Finsler-eset mintájára visszakapható az alapfüggvény (s ilyen értelemben azzal „kompatibilis”) – és amely megnyitja az utat a metrikus differenciálgeometria ismert technikáinak alkalmazásához.
Ezt a problémát Hideyuki Iwamoto japán matematikus oldotta meg 1948-ban ([B2]). Egy általa bevezetett parciális derivált operátor alkalmazásával sikerült explicite leszármaztatnia az alapfüggvényből a kívánt tulajdonságú tenzort. Ezt metrikus 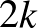 -tenzornak nevezték, alkalmas lokális koordinátarendszerben ugyanis
-tenzornak nevezték, alkalmas lokális koordinátarendszerben ugyanis
![$\displaystyle g_{i_1\dots i_kj_1\dots j_k}=:g_{i[k]j[k]}
$](/images/stories/latexuj/2023-05/2023-05-tamassylajos/img44.png)
alakú komponensfüggvényekkel rendelkezik. Speciálisan szólhatunk két indexes, tehát ![$g_{ij}=g_{i[1]j[1]}$](/images/stories/latexuj/2023-05/2023-05-tamassylajos/img45.png) alakú komponensekkel rendelkező metrikus 2-tenzorokról. Iwamoto azt is megmutatta, hogy ha egy
alakú komponensekkel rendelkező metrikus 2-tenzorokról. Iwamoto azt is megmutatta, hogy ha egy 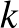 -dimenziós területmértékű areal-téren létezik metrikus
-dimenziós területmértékű areal-téren létezik metrikus 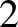 -tenzor (és ez a helyzet, ha
-tenzor (és ez a helyzet, ha 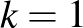 vagy
vagy 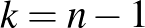 , azaz Finsler- és Cartan-sokaságok esetén), akkor ebből az általa bevezetett metrikus
, azaz Finsler- és Cartan-sokaságok esetén), akkor ebből az általa bevezetett metrikus 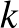 -tenzor előállítható a
-tenzor előállítható a
formula alapján, ahol a jobb oldalon a szögletes zárójelek alternálást jelentenek az 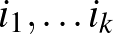 , illetve a
, illetve a 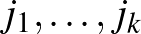 indexekre. Azokat az areal-tereket, amelyeken létezik metrikus
indexekre. Azokat az areal-tereket, amelyeken létezik metrikus 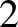 -tenzor és ezzel a (⁎) összefüggés teljesül, metrikus areal-tereknek nevezték. Kawaguchi 1951-ben bebizonyította, hogy ha egy areal-tér metrikus
-tenzor és ezzel a (⁎) összefüggés teljesül, metrikus areal-tereknek nevezték. Kawaguchi 1951-ben bebizonyította, hogy ha egy areal-tér metrikus 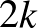 -tenzorának komponenseiből képzett
-tenzorának komponenseiből képzett 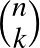 rendű determináns nem tűnik el, s az
rendű determináns nem tűnik el, s az 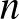 és
és 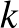 számok relatív prímek, akkor a tenzorból véges számú algebrai operációval metrikus
számok relatív prímek, akkor a tenzorból véges számú algebrai operációval metrikus 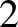 -tenzor származtatható, amely azonban általában nem tesz eleget a (⁎) relációnak ([B3]). Az ilyen tulajdonságú terek alkotják a szubmetrikus areal-terek osztályát. Fölvetődik a kérdés: melyek azok a szubmetrikus areal-terek, amelyek egyúttal metrikusak is? Ezt 1953-ban Kwoichi Tandai definitíve megválaszolta:
-tenzor származtatható, amely azonban általában nem tesz eleget a (⁎) relációnak ([B3]). Az ilyen tulajdonságú terek alkotják a szubmetrikus areal-terek osztályát. Fölvetődik a kérdés: melyek azok a szubmetrikus areal-terek, amelyek egyúttal metrikusak is? Ezt 1953-ban Kwoichi Tandai definitíve megválaszolta: 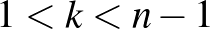 esetén egy szubmetrikus areal-tér akkor és csak akkor metrikus, ha az alapfüggvénye az alapsokaságon adott Riemann-metrikából származik ([B4]).
esetén egy szubmetrikus areal-tér akkor és csak akkor metrikus, ha az alapfüggvénye az alapsokaságon adott Riemann-metrikából származik ([B4]).
Ezzel a kérdéskör lezárulni látszott, az 1970-es évek elején azonban Tamássy Lajos új megvilágításba helyezte a dolgokat ([3], [4]). Alapötletének felvázolása céljából tekintsünk egy 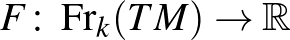
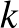 -dimenziós területmértéket, ahol
-dimenziós területmértéket, ahol 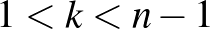 . Az
. Az  sokaságon adott minden
sokaságon adott minden 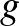 Riemann-metrika indukál egy ilyen területmértéket, jelölje ezt
Riemann-metrika indukál egy ilyen területmértéket, jelölje ezt 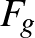 . Kiválasztva egy
. Kiválasztva egy 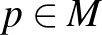 pontot és egy
pontot és egy 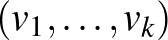
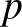 -beli
-beli 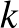 -élt, létezik olyan
-élt, létezik olyan 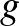 Riemann-metrika, hogy
Riemann-metrika, hogy 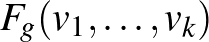
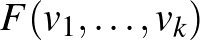 -hoz, jól definiált értelemben, „geometriailag a legközelebb van”. Tamássy Lajos regulárisnak nevezte az areal-teret, ha minimalizáló Riemann-metrika minden
-hoz, jól definiált értelemben, „geometriailag a legközelebb van”. Tamássy Lajos regulárisnak nevezte az areal-teret, ha minimalizáló Riemann-metrika minden 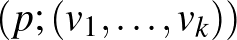 esetén egyértelműen létezik. Approximációs eljárásával, a regularitás feltétele mellett, olyan metrikus
esetén egyértelműen létezik. Approximációs eljárásával, a regularitás feltétele mellett, olyan metrikus 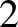 -tenzort konstruált, amelyből a (⁎) formula szerint felépített
-tenzort konstruált, amelyből a (⁎) formula szerint felépített 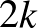 -tenzor kompatibilis az alapfüggvénnyel, megmutatta továbbá, hogy van olyan areal-tér, amelyben a metrikus
-tenzor kompatibilis az alapfüggvénnyel, megmutatta továbbá, hogy van olyan areal-tér, amelyben a metrikus 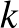 -tenzor nem származtatható Riemann-metrikából.
-tenzor nem származtatható Riemann-metrikából.
Ilyen módon kiderült, hogy a geometriai szempontból igazán érdekes areal-terek osztálya lényegesen bővebb annál, amit az addig elvégzett kutatások sejtettek.
Az 1980-as évektől kezdve Tamássy Lajos növekvő számban publikált Finsler-geometria tárgyú dolgozatokat. E munkák egy része a Finsler-sokaságok egy speciális, az általánosított Berwald-sokaságok alkotta osztályával foglalkozik. Általánosított Berwald-sokaság esetén az alapsokaság – tehát nem annak érintősokasága! – el van látva olyan kovariáns deriválással (=lineáris konnexióval), amelyhez tartozó párhuzamos eltolások megőrzik a vektorok Finsler-normáját. Ha a kovariáns derivált torziómentes, akkor a Berwald-sokaságokhoz jutunk, amelyeket Berwald – igen találó módon – affinösszefüggő Finsler-sokaságokként említett. Szabó Zoltán munkásságának köszönhetően a Berwald-sokaságok teljes osztályozása ismert, az általánosított Berwald-sokaságok világában azonban még nagyon sok a felfedezni való. Vizsgálatukhoz mindenesetre nincs feltétlenül szükség az érintőnyalábon a Finsler-függvényből származó kovariáns deriválásokra; erre utalva Tamássy Lajos gyakran használta a „pont Finsler-tér” elnevezést ([6], [7]) vagy szólt „vonalelemek nélküli Finsler-geometriáról” ([8]). Az általánosított Berwald-sokaságok (összefüggő alapsokaság esetén) ekvivalens módon definiálhatók a következő feltétellel:
Bármely két pont érintőtere között megadható olyan lineáris izomorfizmus, amely az egyik érintőtér indikátrixát (azaz az 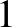 Finsler-normájú vektorok halmazát) a másik érintőtér indikátrixába viszi át.
Finsler-normájú vektorok halmazát) a másik érintőtér indikátrixába viszi át.
Ezt a definiáló tulajdonságot tartva szem előtt, Tamássy Lajos egyszerű geometriai érveléssel megmutatta, hogy az általánosított Berwald-sokaságok egy tág osztálya megkapható lapos (flat) Finsler-sokaságból az indikátrixok centroaffin deformációjával. (Egy Finsler-sokaság lapos, ha a Berwald- és a Riemann-görbülete egyaránt eltűnik.)
Finsler-geometria tárgyú munkáinak további fontos témája volt a Finsler-sokaságok és a (topológiai értelemben vett) metrikus terek vagy távolság-terek kapcsolatának vizsgálata ([9], [10]). Ha egy 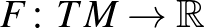 Finsler-függvény reverzibilis abban az értelemben, hogy
Finsler-függvény reverzibilis abban az értelemben, hogy 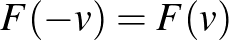 minden
minden 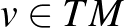 értintővektor esetén, akkor – rendelkezvén a görbeszakaszok ívhossz-mértékével – az
értintővektor esetén, akkor – rendelkezvén a görbeszakaszok ívhossz-mértékével – az  sokaság kézenfekvő módon távolság-térré tehető úgy, hogy a távolság-topológia megegyezzen a sokaság-topológiával. A kiinduló kérdés itt az, hogy
sokaság kézenfekvő módon távolság-térré tehető úgy, hogy a távolság-topológia megegyezzen a sokaság-topológiával. A kiinduló kérdés itt az, hogy
egy  sokaságon adott
sokaságon adott 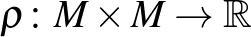 távolságfüggvényből milyen feltételek mellett származtatható olyan
távolságfüggvényből milyen feltételek mellett származtatható olyan 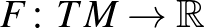 Finsler-függvény, amely a kiindulásul szolgáló
Finsler-függvény, amely a kiindulásul szolgáló 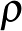 távolságfüggvényt indukálja?
távolságfüggvényt indukálja?
Erre Tamássy Lajos 93 éves korában megjelent utolsó, Kertész Dáviddal közösen jegyzett dolgozatában ([11]) a következő választ adta:
Ha egy 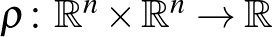 távolságfüggvény bizonyos differenciálhatósági feltételek mellett eleget tesz két, tisztán geometriai, a
távolságfüggvény bizonyos differenciálhatósági feltételek mellett eleget tesz két, tisztán geometriai, a 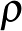 -szférákra és az egyenesek szerepét játszó görbékre vonatkozó feltételnek, akkor létezik olyan, ún. gyenge Finsler-függvény, amely
-szférákra és az egyenesek szerepét játszó görbékre vonatkozó feltételnek, akkor létezik olyan, ún. gyenge Finsler-függvény, amely 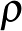 -t indukálja, és ez az
-t indukálja, és ez az
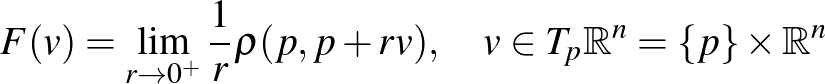
formulával adható meg.
A „gyenge” jelző arra utal, hogy 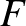 a (K) feltételnél gyengébb konvexitási feltételnek tesz eleget.
a (K) feltételnél gyengébb konvexitási feltételnek tesz eleget.
Visszaemlékezések
„Egyetemi pályafutásom során három kiváló matematikus volt rám meghatározó hatással: Nyikolaj Sztyepánovics Szinjukov Odesszából, Makoto Matsumo Kyotoból, és mindenekelőtt Tamássy Lajos professzor, aki tanszékvezetőm volt. Vezető-, oktató- és kutatómunkáját a pontosság, korrektség és a szakmai igényesség jellemezte. Nagy megtiszteltetés volt számomra, hogy a tanszékvezetői megbízatásban én követhettem. Messzemenően támogatott odesszai tanulmányaimban, majd vezetői tevékenységemben. Matsumoto professzorral való kapcsolatomat is neki köszönhettem. Három évtizedet töltöttem a KLTE Matematikai Intézetében, ezen idő alatt mindig számíthattam megfontolt tanácsaira.”
„60 évvel ezelőtt, I. éves hallgató koromban tanárom volt, az egyik legnehezebb tantárgyunknak, az analízisnek, az előadója. Előadásai mintaszerűek voltak. Szigorú, igényes, korrekt, igazságos és mindenkor emberséges volt tanítványaival. Becsülte a tehetségeket. Úriember volt a szó legnemesebb értelmében. Különös megtiszteltetésnek tekintettük, ahogy minket, fiatalabb munkatársait kollégáivá fogadott. Életem egyik ajándéka, hogy később barátjának tekintett. Szakmai pályám egy-egy nehezebb időszakában mellettem állt, bölcs tanácsokkal támogatott. Ahogy Lajos Bátyámat és életpályáját jobban megismertem, a TANÁR és TUDÓS mellett egyre jobban tiszteltem benne az EMBERT, egyik példaképemmé vált. Átélt nehéz időszakokat, de elveihez mindig hű maradt. Ha kellett, inkább visszahúzódott, a szerényebb érvényesülést választotta, de a tisztességből nem engedett, megalkuvás nélkül haladt az általa helyesnek tartott úton.”
Irodalomjegyzék
(A) Tamássy Lajos dolgozatunkban idézett munkái
- [1] Über den Affinzusammenhang von, zu Tangentialräumen gehörenden Produkträumen, Acta Math. Acad. Sci. Hungar. 1 (1960), 65–82.
- [2] Metric tensors of areal spaces, Tensor N.S. 31 (1977), 165–174.
- [3] On Euclidean osculation of areal spaces, Periodica Math. Hung. 2 (1978), 71–78.
- [4] Direct method to characterize conformally Minkowskian Finsler spaces, Tensor N.S. 33 (1979), 379–384. (M. Matsumoto-val)
- [5] Scalar and gradient vector fields of Finsler spaces and holonomy groups of nonlinear connections, Demonstratio Math. 14 (1981), 551–563. (M. Matsumoto-val)
- [6] The point Finsler spaces and their physical applications in electron optics and thermodynamics, Math. Comput. Modelling 20 (1994), 93–107. (R. S. Ingarden-nel)
- [7] Point Finsler spaces with metrical linear connections, Publ. Math. Debrecen 56 (2000), 643–655.
- [8] Finsler geometry without line elements faced to applications, Reports on Math. Phys. 51 (2003), 233–250. (Kozma Lászlóval)
- [9] Finsler geometry in the tangent bundle, Advanced Studies in Pure Math. 48 (2005), 163–194.
- [10] Relation between metric spaces and Finsler spaces, Diff. Geom. Appl. 26 (2008), 483–494.
- [11] Differentiable distance spaces, Acta Math. Hungar. 148 (2016), 405–424. (Kertész Dáviddal)
(B) Egyéb hivatkozások
[B1] Élie Cartan, Les espaces métriques fondés sur la notion d'aire, Hermann, Paris, 1934.
[B2] H. Iwamoto, On geometries associated with multiple integrals, Math. Jap. 1 (1948), 74–91.
[B3] A. Kawaguchi, On areal spaces III, Tensor N. S. 1 (1951), 89–101.
[B4] K. Tandai, On areal spaces VI, Tensor N. S. 3 (1953), 40–45.
Debreceni Egyetem Matematikai Intézet












![$\displaystyle g_{i_1\dots i_kj_1\dots j_k}=g_{[i_1[j_1}\dots g_{i_k]j_k]}$](/images/stories/latexuj/2023-05/2023-05-tamassylajos/img48.png)