A tudományterületek között nincsenek határok

Hogyan lett belőled matematikus?

Nagyjából ötödikes voltam, amikor kiderült az iskolában, hogy elég jó vagyok matematikából. Ezért jelentkeztem a Kis Matematikusok Baráti Körébe, ide jártam általános iskolás koromban. A KMBK országos hálózat volt, területi szakkörökkel, és minden évben volt egy verseny, területi, megyei, országos döntővel, amit hatodikos koromban megnyertem. Édesanyám a Móricz Zsigmond Gimnáziumban tanított, kolléganője, jó barátnője Némethy Katalin volt az első, aki ráébresztett egy más szintű matematikára. Először is, kezembe adta Péter Rózsa Játék a végtelennel-jét. Másodszor, amikor a KMBK versenyén 500 forintot nyertem, nyakoncsípett, bevitt a nagy könyváruházba a Rákóczi úton, és elvásároltuk az összes pénzt matekkönyvekre. Én tartottam a két kosarat, Kati néni pedig villámgyorsan dobálta bele a „szükséges” könyveket. 500 forint nagy pénz volt akkor: most éppen kezemben tartom Coxeter-Greitzer Újrafelfedezett geometriáját (kissé rongyos már), amit akkor vettünk 22 forintért. Harmadszor, elhívott magához, hogy szerkesztéseket mutat nekem. Én megjelentem körző- és vonalzókészlettel, ahogyan az iskolai órán elvárták. Kati néni közölte, hogy erre semmi szükség, és nagy szürke csomagolópapíron egy vastag tintaceruzával felvázolta a Feuerbach-kört. Persze semmi nem volt egyenes vagy pontosan kör alakú, az iskolából kivágtak volna egy ilyen trehány ábrával, viszont a lényeg rajta volt. Ez a jelenet, ahogy értetlenül fogom a feleslegessé vált körzőt, vonalzót a nagy szürke csomagolópapír előtt Kati néni sötét nappalijában, máig élesen bennem maradt. De megtudtam belőle a lényeget: a kör és az egyenes egy absztrakció. Nem az ábrának kell precíznek lennie, hanem a mögötte lévő gondolatnak.

Tehát a következő lépés a speciális matematika tagozatos gimnázium lett.

Akkoriban három ilyen középiskola volt Budapesten: a Fazekas, az István és a Berzsenyi. Egyrészt azért mentem a Berzsenyibe, mert ez volt a lakásunkhoz a legközelebb, de a fő ok Pataki János volt: ő volt az első évben a tanárom. Némethy Kati néni javasolta ugyanis azt is, hogy jelentkezzek a Berzsenyi Gimnáziumba, van ott egy fiatal, zseniális matektanár, menjek hozzá. Benne volt egy picit talán az is, hogy a Fazekasnak az volt a híre, hogy az „versenyistálló”, a Berzsenyi talán egy picit életközelibb, ott nemcsak a matematika számít. Nekem nagyon jó osztályom volt, legközelebbi barátom és padtársam, Engländer János. Érdekes, hogy tőlem rendszeresen megkérdezik, de nekem nincs rokoni kapcsolatom Erdős Pállal, szemben Engländer Jancsival (Erdős eredeti neve Engländer). A Berzsenyi nagyszerű hely volt, kiváló osztályközösségünkből végül öten lettünk matematikusok, de máig az akkori osztálytársakkal vagyok a legjobb barátságban. Fantasztikus matematikatanáraink voltak: Pataki, az osztályfőnökünk, nagyon nagy egyéniség volt, rengeteget kaptunk tőle emberileg is… nagyon fájt, hogy egy év után otthagyott minket, elment az iskolából. Helyette jött Urbán János és Herczeg János, akiket szintén nagyon szerettünk. Mindhárman nagyszerűek voltak, másképpen. Tanított még Bényei Károly is, akitől féltünk egy kicsit – roppant szigorú volt trigonometriában –, sajnos Némethy Katalinnal, Urbán Jánossal együtt nincs többé közöttünk.

Még egy ikonikus tanárról kell megemlékeznem, aki végig követte az utamat: Reiman Istvánról. Pista bácsi hatását talán nem kell bemutatnom, egy óriás volt, és a Reiman-szakkör minden második péntek délutánonként egy szentély. Már elsős (mai kilencedikes) koromtól jártam, Szalai Jancsi barátom vitt el, aki a Fazekasba járt, és nálam két évvel volt idősebb, az érettségi előtt egy évvel. Vele még 1978-ban a KMBK országos versenyen ismerkedtem meg, amit a zánkai úttörőtáborban rendeztek, és ahol őrséget is kellett adnunk. Jancsi egyetlen kétórás őrség alatt elmagyarázta nekem a logaritmust, majd a második kétórás őrségben a teljes trigonometriát. Közben felőlünk az egész tábort elvihették volna…Viszont az első két évben meg se mertem szólalni a Reiman-szakkörön, hiszen ott voltak a nálam két-három évvel idősebbek. Végül a harmadik év elején összeszedtem minden bátorságomat, jelentkeztem az egyik házi feladat elmondására (amiben biztos voltam), és Pista bácsi a nevemen szólított. Nem tudom, honnan tudta, talán rákérdezett valakitől, nyilván látta, hogy két éven át mindig ott voltam, de megvárta, amíg én nyílok meg.

A Reiman-szakkör mellett ott voltak a versenyek, amelyeken nagyon jól szerepeltél. A KöMaL-ban például nemcsak a matematika, de a fizika feladatokat is megoldottad, és az archívumban azt is felfedeztem, hogy később, egyetemista korodban cikkeid is megjelentek.

A KöMaL-nak a középiskola alatt óriási szerepe volt, permanens versenyhelyzetet teremtett. Volt, amikor a Nyugati főpostáján a beadási határidő késő estéjén írtam le az utolsó feladatot a postásoktól kunyerált papírra. Azt is Pataki Jancsitól tanultuk, hogy indigóval írjuk a feladatokat, hogy össze tudjuk hasonlítani később a megoldásokat. Egyébként többen jártunk akkoriban a főpostára…

A fő irányom mindig a matematika volt, de az összes fizikaversenyen is elindultam, volt, amikor az jobban sikerült, mint a matematika (például érettségi előtt egy évvel a Kürschák nagyon nem sikerült, viszont az Eötvös fizikaversenyen harmadmagammal megosztva első lettem).

Volt egy különleges Kürschák-verseny, ahol nyolcadmagaddal lettél első helyezett.

Könnyűnek sikerültek a feladatok 1983-ban, nyolcan is megoldottuk mindegyiket. Viszont 1984-ben már egyedül nyertem, ráadásul 3 napra hazaengedtek Lentiből a katonaságtól!

Ekkor már előfelvételit nyertél az ELTE TTK matematikus szakára.

Akkor még ezen az „elit” szakon nagyon válogatott társaság volt, nem százfős évfolyam. Mi 28-an kezdtük, 22-en végeztünk, Engländer Jancsi mellett (aki Coloradoban professzor) évfolyamtársam volt Szabó Zoltán (most Princetonban professzor) Kovács Sándor (Seattle-ben professzor), Sárközy Gábor, aki részben Amerikában, részben otthon a Rényi Intézetben dolgozik, Szabó Tibor, aki Berlinben professzor, az ELTE-n tanító Karátson János, Kovács Ágnes, Simon Péter, Pfeil Tamás, szóval voltak közülünk jópáran, akik igazi matematikus karriert csináltak, és voltak persze, akik elhagyták a kutató matematikát.

Milyen volt az egyetemi oktatás a 80-as évek második felében?

Bennünket még tanított többek között Lovász, Babai, Lempert László, Beck József, az akkori középgeneráció derékhada. Ránk sokkal több egyéni figyelem jutott. A felső matematikus évfolyamból úgy 4-5 embernek engedték meg, hogy szoros felügyelet mellett pl. elsőéves tanárszakosoknak gyakorlatot tartsunk. Engem Gyarmati Edit és Freud Róbert „felügyelt” – lazsálni nem lehetett. Bejöttek az óráinkra, tanácsokat adtak, követték, hogyan, mit csinálunk. Olyan izgalommal készültem a gyakorlataimra, mint a vizsgákra.

Miután az egyetemi Schweitzer-versenyeken is a legjobbak között voltam, így természetes volt, hogy diploma után következik a PhD, hogy hova, abban a rendszerváltásnak nagy szerepe volt. Negyedévesen, amikor specializálódni kellett, egyéni szakot választottam, Szász Domokosékhoz csatlakoztam. (Arnold: Klasszikus mechanika matematikai módszerei c. könyve ugyanis megfogott, nyilván mert érdekelt a fizika.) Domáék kis bensőséges csoportjának kutatásai akkor kevésbé voltak népszerűek Magyarországon, de az hamar látszott, hogy komolyak és a világban fontosnak tartják őket. Nekik alapjában moszkvai egyetemi kapcsolataik voltak, ő is, Krámli András is Moszkvában végeztek. Ha nem lett volna 1989, szinte biztos, hogy én is oda kerülök. Jakov Sinai, a dinamikai rendszerek atyaúristene – valószínűleg hozzá mentem volna ki PhD tanulmányokra. Azonban másképp alakult.

Hogyan juthatott ki valaki 1990-ben az ELTÉ-ről Princetonba PhD tanulmányokra?

1989-90-ben már „egyszerű” volt, hisz akkorra már volt világútlevél, amerikai ösztöndíjak pedig mindig is voltak. Előttem 2-3 évvel még nehezebb volt. Az sokat segített nekem, hogy olyanok írtak rólam ajánlóleveleket (Szász Domokos, aki a témavezetőm volt, és Lovász László), akiket ismertek Princetonban. A rendszerváltás éveiben már világos volt, hogy kinyílnak a kapuk, elsődlegesen Amerikába lehetett menni. A mi évfolyamunknak körülbelül a fele kiment külföldre doktori ösztöndíjakkal.

Ma már sokan nem magyar, hanem külföldi egyetemekre jelentkeznek. A legtehetségesebbek már az alapképzés után elmennek itthonról, és az MSc-t és a doktori fokozatot már külföldi ösztöndíjakkal szerzik meg, utána pedig több évet töltenek kint posztdoktori állásokban. Van, aki hazajön, és van, aki nem. Aki itthon marad, az hátrányba kerül?

Ma nagyon sokan már az érettségi után kimennek, tipikus, hogy Cambridge-ből és Oxfordból idejönnek, és elviszik a Fazekas osztályának az egyharmadát, ez Magyarországnak nyilván veszteség. Az ELTE matematikusképzésének színvonala a mi időnkben sokkal jobb volt, mint manapság. Nem látok igazán bele, hogy mi az oka, de eleve az a struktúra, hogy volt egy 28 fős évfolyam, azt is két csoportra osztották, és a legjobb tanárok foglalkoztak velünk. Az abszolút presztízs volt az egyetemen, hogy ki taníthatja a matematikusokat. A gyakorlatvezetőink sem diákok voltak, hanem mind elismert matematikusok. Azt hiszem, sokkal jobban figyeltek ránk. Több jó professzor volt, és kevesebb diák. Most nem tudom, hány embert vesznek fel, 80-100 fő nyilván túl sok, ennyi jó matematikus nem születik egy-egy évben. Úgy vélem, hogy minden évfolyamban kb. tízen vannak, akikből kutató matematikus lehet. Nem vagyok biztos abban, hogy avval a tízzel most ugyanolyan szinten tudnak foglalkozni, mint ahogy a mi időnkben. Legfontosabbak voltak nálunk a specik a reguláris órákon túl: rengeteg ilyen volt, nemcsak az egyetemi tanárok, hanem a Matematikai Kutatóintézetből (ma Rényi Intézet) is sokan tartottak speciálelőadásokat. Negyed-, ötödévben én például 5-6-7 specire is jártam, és a többiek is. Azt hiszem, ezek most nincsenek ilyen mennyiségben. Nyilván benne van az is, hogy sok jó matematikus elment itthonról, de az itthon maradott egyetemi oktatók óraszám- és adminisztratív terhelése is sokkal nagyobb, százával kell elbírálniuk a diplomamunkákat, sokkal inkább elmentünk a tömegoktatás irányába, és ez az elitoktatás kárára ment.

Ez más országokban is így változott?

Azt hiszem, külföldön ez korábban is így volt. A rendszerváltás előtt mi privilegizált helyzetben voltunk: az egyszakos tudományos egyetemi képzésünk egészen biztos, hogy magasabb színvonalú volt, mint amit az ország akkori gazdasági helyzetéből gondolni lehetett volna. A matematikaoktatásunk akkor világszínvonalú volt, mind a középiskolai tehetséggondozás, mind az ELTE egyetemi képzése tekintetében. Ezért is volt az, hogy miután kimentünk PhD-zni, akkor mi úgy éreztük, hogy megálljuk a helyünket és legalább olyan volt az előképzettségünk, mint a többieknek, akik más, akár amerikai elitegyetemekről jöttek. Franciaországban az école préparatoire a mienkhez hasonlóan nagyon színvonalas, Moszkvában volt még elit matematikusképzés, és még egy-két amerikai egyetemen, Princetonban, a Harvardon, de az első diploma szintjén ez alapvetően korábban nem volt jellemző a nyugati országokban. Nyugat-Európában sokkal hamarabb elindították a tömegoktatást, már a hatvanas évektől.

A doktori fokozatod megszerzése után több neves intézményben is dolgoztál, mint az ETH Zürich, a Courant Institute, a GeorgiaTech. Mostani munkahelyed, az Institute of Science and Technology Austria matematikai vagy inkább természettudományi intézet?

2005-ben Ausztria egy komoly tudománypolitikai döntéssel zöldmezős beruházásként egy teljesen új természettudományos kutatóintézet létrehozását kezdeményezte, a Weizmann Intézet mintájára. Így alapították meg 2007-2008-ban az IST-t. Az intézet célja kimondottan interdiszciplináris: „Nálunk a tudományterületek között nincsenek határok”, ez van kiírva nagy betűkkel a bejáratánál. Az IST optimálisan ötvözi az amerikai es európai tudományos struktúrák pozitívumait. Mint új es rugalmasan felépített, viszonylag kicsi intézmény, nálunk jóval kevesebb a bürokrácia, mint egy nagy egyetemen. Mivel csak posztgraduális diákjaink vannak, a tanítási kötelezettség minimális. Lehetőség van arra, hogy a semmiből építsünk fel valamit, így „begyöpösödött” hagyományok nem kötnek abban, hogy milyen irányban fejlődjünk, milyen területekről vegyünk fel új kollégákat. Sokan dolgoznak közülünk ténylegesen interdiszciplinárisan, elsősorban a számítástudomány határán (például Computation and Neuroscience), de vannak teljesen elméleti kutatócsoportok, pl. algebrai geometriai, számelméleti stb. Azért mindig harcolni kell egy kicsit, hogy az interdiszciplinaritás és a tiszta tudományok is képviselve legyenek.

IST-Austria Campus — Az IST Austria kampusza

Hogyan kerültél ide?

A megalakulás óta folyamatosan volt felvétel, tehát az állásaik meg voltak hirdetve, jelentkeztem, felvettek és itt dolgozom 2013 óta. Én már korábban szerettem volna Bécsbe jönni, elsősorban a földrajzi közelség miatt.

Így többet jársz Magyarországra?

Igen, ma délután is épp megyek haza. A szüleim Budapesten élnek. Én fokozatosan jöttem visszafelé: Amerikában voltam elég sokáig, utána lehetőségem volt Münchenbe menni, ahol állandó professzori állásom volt. Ha nem lett volna ez az új intézet, valószínűleg ott maradok.

Milyen a szakmai kapcsolatod a magyar matematikával?

Tartom a kapcsolatot a régi iskolával, Szász Domokosékkal (Krámli András már nem él sajnos), Tóth Bálinttal. Ez nem azt jelenti, hogy együtt dolgozunk, amit én csinálok, az az ő területüktől már eltávolodott, de figyeljük egymás munkáját. Ezen kívül, mivel közel vagyok, Bécsben, néha felkérnek magyarországi szakmai pályázatok bírálatára, illetve bizottsági tagságra. Nyilván avval, hogy külföldön vagyok, bizonyos fokig pártatlanabbul, elfogulatlanabbul tudok részt venni pályázatok elbírálásában, ezért szoktak felkérni.

2017-ben megkaptad az Amerikai Matematikai Társaság (AMS) Leonard Eisenbud Prize for Mathematics and Physics elnevezésű díját. Nemrég pedig újabb elismerésként a Schrödinger-díjat. Milyen rangúak ezek a kitüntetések?

Az Eisenbud-díj az AMS háromévenként kiadott tematikus díja matematikai fizikából, nagyjából 15 hasonló díj van a matematika egy-egy nagyobb területére fókuszálva. Persze ezek jóval alatta vannak az igazán nagy matematikai díjaknak, mint az Abel-díj, a Wolf-díj, a Kyoto Prize vagy a Fields medal. A Schrödinger-díj az Osztrák Tudományos Akadémia matematikai-természettudományi éves nagydíja, annyiból széleskörű, hogy nemcsak a matematikát, hanem a teljes természettudományt felöleli (az osztrák akadémiának két osztálya van: természettudományi/matematikai és humán), viszont nem nemzetközi, tehát ausztriai tudományos tevékenységért adják.

Azóta másodszor is elnyerted az ERC Advanced Grant támogatását is, ehhez is gratulálok! Kutatási területed a matematikai fizika, a véletlen mátrixok. Szeretném, ha beszélnél róla.

Az IST struktúrájának alapegysége a csoport (nem tanszék, mint az egyetemeken), vannak kisebbek és nagyobbak. Az én csoportomban most épp három ember van, de ősszel jön még kettő, volt, amikor hatan voltunk, mindig van fluktuáció. A csoportomon belül a kutatás fő iránya most már évek óta a véletlen mátrixok. Én alapjában véve matematikai fizikus vagyok, ami egy ennél tágabb terület, fizikai eredetű matematikai problémák matematikailag precíz bebizonyításáról szól. Amit a fizikusok úgy nagyjából tudnak, vagy ad hoc, nem szigorú módszerekkel bizonyítottak, azokat mi precíz módon matematikai eszközökkel megcsináljuk. Ezen belül már 10 éve a véletlen mátrixokkal foglalkozom, ami egy nagyon érdekes terület, fizikai motivációja eredetileg Wigner Jenőtől származik, de maga a kérdéskör, tehát amit vizsgálunk, az tiszta matematikai. Tréfásan azt szoktam mondani, hogy mi matematikusok szégyellhetjük magunkat, hogy egy fizikusra volt szükség ahhoz, hogy ezt a kérdést egyáltalán feltegyük. A kérdést, ami a véletlen mátrixokról szól, nyugodtan feltehette volna egy matematikus is: az ugyanis a lineáris algebra és a valószínűségszámítás természetes határmezsgyéje. Azonban az ötvenes évek elején még a valószínűségszámítás eléggé mostohagyereke volt a matematikának, akkoriban „komoly” matematikusok nemigen foglalkoztak vele. Így nem merült fel az a természetes kérdés, hogy mi történik, ha véletlenséget rárakunk valami más, létező matematikai struktúrára, mint például a mátrixokra. Mára azóta ebből szinte „iparág” lett, mindenből csinálnak véletlent, vannak véletlen gráfok, véletlen csoportok, véletlen metrikák, gyakorlatilag bármilyen korábban létezett területe a matematikának vizsgálható valószínűségszámítási módszerekkel is. Erdős Pali bácsinak volt az egyik nagy találmánya, hogy véletlen struktúrák bizonyítási eljárást, bizonyítási módszert is adnak egyúttal. Az a gondolat, hogy valószínűségszámítást ötvözni a matematika egy más területével, azóta nagyon ígéretes, gyümölcsöző lett. A véletlen mátrixok spektrumának univerzalitása nagyon régóta nyitott sejtés volt, ez, amit mi megoldottunk a régebbi témavezetőmmel, Horng-Tzer Yauval közösen több mint 10 évvel ezelőtt, és ezzel kapcsolatban egy módszert fejlesztettünk ki, amit azóta is használunk további, még bonyolultabb hasonló feladatok megoldására.

Véletlen mátrixok

Tekintsünk egy 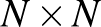$N\times N$ -es szimmetrikus 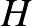$H$ mátrixot, amelynek az elemeit véletlenszerűen választjuk. A legegyszerűbb, ha minden 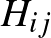$H_{ij}$ mátrixelemet azonos eloszlásból (példaul egy érme feldobásával generált Bernoulli-eloszlás szerint, vagy a standard normális eloszlás szerint) veszünk egymástól függetlenül, persze betartva a szimmetria követelményét, 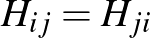$H_{ij}= H_{ji}$ . Ezután kiszámoljuk a 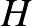$H$ valós sajátértékeit, 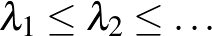$\lambda_1\le \lambda_2 \le \ldots$ , amelyek véletlen számok lesznek, növekvő sorba rendezve:

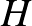$\displaystyle H$ mátrix 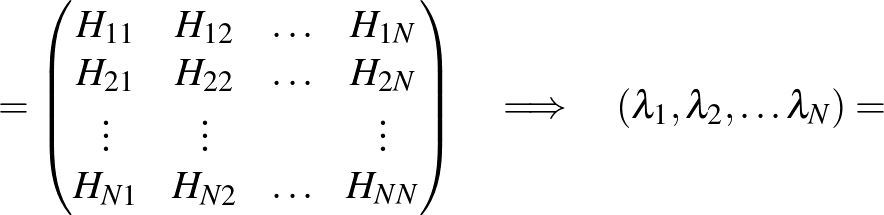$\displaystyle =\begin{pmatrix} H_{11} & H_{12} & \ldots & H_{1N}\\ H_{21} & ... ...{pmatrix} \quad\Longrightarrow \quad (\lambda_1, \lambda_2, \ldots \lambda_N) =$ sajátértékek $\displaystyle .$

Jóllehet a mátrix elemeinek eloszlása nagyon egyszerű (függetlenek), az általuk generált eloszlás a sajátértékeken felettébb nemtriviális lesz. Többek között a szomszédos sajátértékek taszítják egymást (mindenkinek javaslom ezt a legegyszerűbb 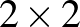$2\times 2$ -es példán bebizonyítani), vagyis a sajátértékek egy erősen korrelált pontfolyamatot alkotnak. Ennek a folyamatnak a statisztikája nagyon más, mint a legegyszerűbb Poisson pontfolyamaté, amely független pontokbol áll. Miért érdekes ez?

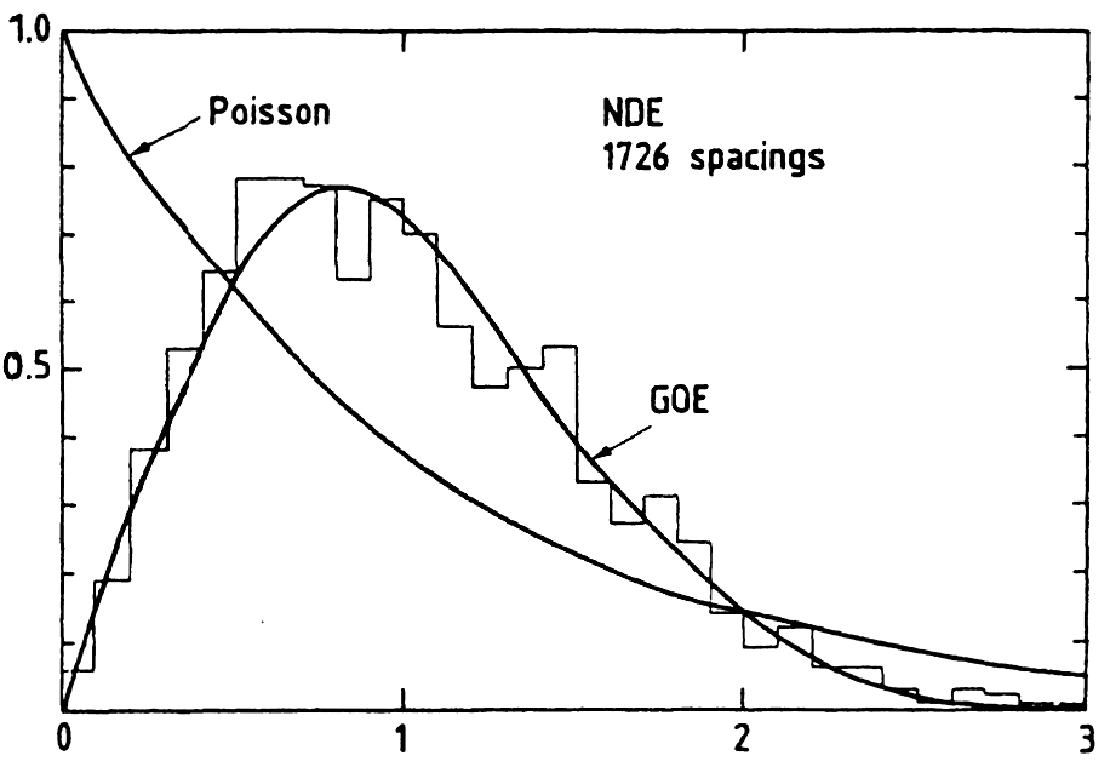
Wigner Jenő az 1950-es években a nehéz atommagok laboratóriumban mért spektrumát vizsgálva észrevette, hogy a szomszédos energiaszintek közötti távolságok statisztikája egy univerzális struktúrát követ: függetlenül attól, hogy éppen melyik atommagot nézte, és annak spektrumán belül melyik energiatartományt, az ún. gap statistics ugyanaz volt! Mindez még az atommagok fizikáját pontosan leíró standard modell előtt történt, de Wigner joggal feltételezhette, hogy az energiaszintek egy Hamilton-operátor sajátértékeinek felelnek meg. Ezt szerette volna modellezni, s mivel azt sejtette, hogy egy teljesen univerzális statisztikára talált, egyszerűen a valódi, s akkor még ismeretlen Hamilton-operátort egy véletlen mátrixszal helyettesítette. S valóban, a véletlen mátrix ugyanazt a statisztikát adta!

A matematikai feladatot tehát úgy lehet megfogalmazni, hogy egy nagy véletlen mátrix sajátérték-különbségeinek statisztikája, persze megfelelően átskálázva, független a mátrixelemek eredeti eloszlásától, vagyis pl. a közepső gap eloszlásfüggvénye a nagy $N$ limeszben

$\displaystyle \lim_{N\to\infty} \mathbf{P} \left(\frac{\lambda_{N/2+1} - \lambda_{N/2}}{\mathbf{E}[\lambda_{N/2+1} - \lambda_{N/2}]} \ge s\right)\to F(s)$

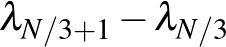egy univerzális $F(s)$ függvény. Ugyanezt az eloszlásfüggvényt kapjuk, ha mondjuk a $\lambda_{N/3+1} - \lambda_{N/3}$ különbséget nézzük (a spektrum szélén lévő sajátértékek kicsit másképp viselkednek). Az egyetlen dolog, amitől $F$ függ, az a mátrix szimmetriaosztálya: a valós szimmetrikus mátrixok esete eltér a komplex hermitikus mátrixokétól. Ezt a sejtést matematikailag precízen a 60-as évek végén Dyson es Mehta fogalmazta meg, és mintegy 50 évvel kesőbb sikerült Horng-Tzer Yauval bebizonyítanunk.

Házi feladat: bizonyítsuk be az 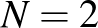$N=2$ normális eloszlás esetében, hogy a $2\times 2$ -es mátrix két sajátértéke erősebben taszítja egymást a komplex esetben, mint a valós esetben.

Segítség. Vegyük észre, hogy a két sajátérték különbsége

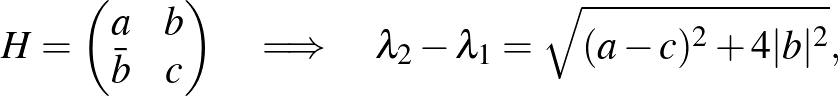
$\displaystyle H= \begin{pmatrix}a & b \cr \bar b & c \end{pmatrix} \quad \Longrightarrow \quad \lambda_2-\lambda_1 = \sqrt{ (a-c)^2 + 4\vert b\vert^2},$

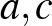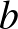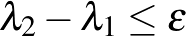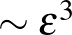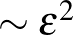és gondoljuk meg hogy ha $a, c$ valós normális eloszlású, viszont $b$ valós vagy komplex (a szimmetriaosztálytól függően) akkor mennyivel kisebb az esélye annak hogy $\lambda_2-\lambda_1\le \epsilon$ a komplex esetben ( $\sim \epsilon^3$ ), mint a valós esetben ( $\sim \epsilon^2$ ).