Ötven éve, 1974-ben hunyt el Kertész Andor algebraprofesszor. Ebből az alkalomból rendezett emlékülést 2024. június 13-án a Debreceni Egyetem Matematikai Intézete és a Magyar Tudományos Akadémia Debreceni Területi Bizottságának Matematikai Munkabizottsága. Az emlékülésről szóló beszámoló előtt röviden ismertetjük Kertész Andor szakmai életútját, majd bemutatjuk a normáltranszverzálisok alaptételéről szóló, Szele Tiborral közös cikkében szereplő bizonyítását.
Kertész Andor rövid szakmai életútja
Kertész Andor 1929. február 19-én született Gyulán. 1947-ben érettségizett a Gyulai Római Katolikus Karácsonyi János Gimnáziumban és felvételt nyert a Debreceni Tudományegyetemre, ahol 1952-ben matematika–fizika–ábrázoló geometria szakos tanári oklevelet szerzett.
Az időközben Kossuth Lajos Tudományegyetemmé átnevezett egyetem Algebra és Számelmélet Tanszékén végigjárta a ranglétra fokait, 1960 és 1968 között tanszékvezető, egyetemi tanárrá 1963-ban nevezték ki. 1962-től 1963-ig, majd 1968-tól 1971-ig vendégprofesszor volt a Halle-Wittenbergi Martin Luther Egyetemen (Martin-Luther-Universität Halle-Wittenberg).
Szele Tibor vezetésével már egyetemi hallgatóként bekapcsolódott az algebrai kutatásokba, amit élete végéig magas szinten folytatott. Legtöbb eredményét az Abel-csoportok, a modulusok és a gyűrűk elméletében érte el. 1954-ben az Operátormodulusok és féligegyszerű gyűrűk című értekezésével a matematikai tudományok kandidátusa, 1957-ben Az operátormodulusok általános elméletéhez című disszertációja alapján pedig a matematikai tudományok doktora lett.
Szakkönyvei közül csak az Artin-gyűrűkről szóló Vorlesungen über artinsche Ringe címűnek az 1968-as megjelenését érhette meg, amelyért 1971-ben nívódíjban részesült. Ennek angol nyelvű, átdolgozott és bővített kiadása (Lectures on Artinian Rings) csak 1987-ben készült el úgy, hogy néhány kiegészítő fejezetet Gerhard Betsch, Alfred Widiger és Wiegandt Richárd írtak meg Kertész Andor ötleteit és szándékát követve. Halála előtt nem sokkal zárta le a Jyväskylä-i Egyetemen 1971-ben tartott 16 órás előadássorozata alapján született Einführung in die transfinite Algebra című kéziratát, amely 1975-ben jelent meg. Végül a Georg Cantorról szóló könyvéről az emlékülés egyik előadása kapcsán, az alábbiakban ejtünk majd szót.
1955-től haláláig szerkesztője volt a Publicationes Mathematicae Debrecen, valamint alapító szerkesztője az 1971-ben indult Beiträge zur Algebra und Geometrie folyóiratnak.
Szakmai munkásságát 1953-ban a Bolyai János Matematikai Társulat első alkalommal odaítélt Grünwald Géza-emlékdíjával, 1968-ban az MTA Akadémiai Díjával ismerték el. Ugyancsak 1968-ban tagjai közé választotta a Leopoldina Német Természettudományos Akadémia (Deutsche Akademie der Naturforscher Leopoldina).
Hosszan tartó betegséget követően, 1974. április 3-án hunyt el Budapesten. A Publicationes Mathematicae Debrecen folyóiratban egy nekrológ [2], később a tudományos munkásságát bemutató cikk [12] jelent meg róla.
Az elmúlt évtizedekben, születésének vagy halálozásának évfordulóihoz kötődően több alkalommal rendeztek tiszteletére emléküléseket Debrecenben. Ezenkívül 1988 óta matematikaverseny viseli a nevét Heves megyében, 2000-ben édesapjával közös emléktáblát avattak a gyulai házuk falán, 2010-ben pedig Kertész Andornak szentelték a Georg Cantor Egyesület (Georg-Cantor-Vereinigung) Georg Cantor Heft nevű kiadványának egy különszámát [1].

Beszámoló az emlékülésről
A 2024. június 13-ai megemlékezés a Debreceni köztemetőben kezdődött, ahol a résztvevők megkoszorúzták Kertész Andor sírját. Itt Vincze Csaba, a Matematikai Intézet igazgatója mondott beszédet. Egyebek mellett felhívta a figyelmet arra, hogy Kertész Andor életének keretei különös módon ágyazódnak be az idén 100 éves debreceni felsőfokú matematikaoktatás történetébe: halálának éve éppen felezőpontja az egy évszázadnyi hosszú útnak, születési éve pedig a Matematikai Tanszék megalakulásának időpontjával esik egybe [13].

Az MTA Debreceni Területi Bizottság székházában rendezett emlékülésen három előadás hangzott el:
 Győry Kálmán: Kertész Andor életútja – személyes emlékekkel
Győry Kálmán: Kertész Andor életútja – személyes emlékekkel
 Nyul Gábor: Kertész Andor néhány, nem tisztán algebrai cikkéről
Nyul Gábor: Kertész Andor néhány, nem tisztán algebrai cikkéről
 Remete László: Steinitz egy tételének Kertész Andor-féle bizonyítása
Remete László: Steinitz egy tételének Kertész Andor-féle bizonyítása

Győry Kálmán először áttekintést adott Kertész Andor életének és szakmai pályafutásának főbb állomásairól. Ezt követően személyes emlékeit osztotta meg a hallgatósággal egykori tanáráról, kollégájáról és barátjáról. Felidézte korrektségét és udvariasságát, továbbá hogy előadásai mindig világosan és logikusan felépítettek, szabatosan és választékosan megfogalmazottak, tartalmilag pedig naprakészek voltak. Elmesélte, hogy Kertész Andor nagydoktorként is részt vett egy hallgatók számára szervezett építőtáborban Bodrogkeresztúron, ahol együtt lakott és dolgozott tanítványaival, túrázás közben pedig közvetlen hangulatú beszélgetéseket tudtak egymással folytatni. Később vezetőként nemcsak tudományos előadásokat, hanem külföldi utazásokról szóló élménybeszámolókat, kirándulásokat, közös budapesti színházlátogatást is szervezett.
Nyul Gábor három témát járt körül. A normáltranszverzálisokkal kapcsolatos részről a jelen munka záró szakaszában még részletesebben lesz szó. A halmazelmélet Zermelo–Fraenkel-féle axiomatikus felépítése esetén fontos szerepet játszik a kiválasztási axióma. Ennek számos ekvivalense közül a legnevezetesebbek a jólrendezési tétel (amely lehetőséget ad a transzfinit indukció alkalmazására) és a Zorn-lemma. Hajnal András és Kertész Andor algebrai ekvivalenseket találtak, például hogy minden nemüres halmazon megadható kancellatív grupoid, továbbá itt algebrai struktúraként mondhatunk akár kancellatív félcsoportot, kancellatív Abel-félcsoportot, kvázicsoportot, hurkot, csoportot, Abel-csoportot, sőt gyűrűt, kommutatív gyűrűt vagy integritási tartományt [3] (másik bizonyítást ld. [9]). Kertész Andor foglalkozott matematikatörténettel is, elsősorban Georg Cantor német matematikus életének és munkásságának feltárása volt szívügye. Ezzel összefüggésben írt cikket a valós számok egzakt bevezetésének százéves jubileuma alkalmából [8], valamint Cantor ötleteinek jelentőségéről az algebra fejlődése szempontjából [7]. Halála után jelent meg a Cantorról szóló könyve, amelynek előszava 1971-es dátumozású, a felépítés tervezete és az egyes fejezetek többé-kevésbé készen voltak, a benne szereplő illusztrációkat, fényképeket és leveleket ő maga gyűjtötte, de a végleges szerkesztést már Manfred Stern végezte el [10]. Azonban még ennél is többet tett Halléban Cantor emlékének ápolásáért, neki köszönhetően került emléktábla Cantor lakóházára, illetve az ő tervei alapján készítette el a szobrászművész egy emlékmű Cantorra vonatkozó oldalát.
Remete László előadása Steinitz következő testelméleti tételéről szólt: Ha az 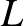 test a
test a 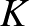 test bővítése,
test bővítése, 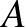 és
és 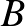 pedig
pedig 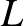 -nek olyan részhalmazai, amelyek algebrailag ekvivalensek
-nek olyan részhalmazai, amelyek algebrailag ekvivalensek 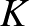 felett, továbbá mindkettő algebrailag független
felett, továbbá mindkettő algebrailag független 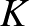 felett, akkor
felett, akkor 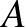 és
és 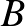 számossága megegyezik.1 Ernst Steinitz eredeti bizonyításában a jólrendezési tételre támaszkodva transzfinit indukciót használt. Később Rédei László a jólrendezést megkerülve, a Zorn-lemma és a kicserélési tétel segítségével igazolta az eredményt. Kertész Andor két további bizonyítást is adott a tételre: az egyik szintén a kicserélési tételre vezeti vissza az állítást, viszont a jólrendezési tételnek egy számosságokra vonatkozó következményét használja fel [4]; a másik, mind közül talán a legegyszerűbb viszont csak a Zorn-lemmára és a Schröder–Bernstein-tételre épít [6]. Az utóbbinak ráadásul előnye, hogy az algebrai ekvivalenciának és algebrai függetlenségnek a definícióit nem, csak bizonyos tulajdonságaikat használja fel. Ezért Kertész észrevétele szerint hasonlóképpen alkalmazható az ekvivalencia és függetlenség absztrakt változataira, ennek következményeként pedig könnyedén adódnak belőle például csoport- és gyűrűelméleti eredmények is [5].
számossága megegyezik.1 Ernst Steinitz eredeti bizonyításában a jólrendezési tételre támaszkodva transzfinit indukciót használt. Később Rédei László a jólrendezést megkerülve, a Zorn-lemma és a kicserélési tétel segítségével igazolta az eredményt. Kertész Andor két további bizonyítást is adott a tételre: az egyik szintén a kicserélési tételre vezeti vissza az állítást, viszont a jólrendezési tételnek egy számosságokra vonatkozó következményét használja fel [4]; a másik, mind közül talán a legegyszerűbb viszont csak a Zorn-lemmára és a Schröder–Bernstein-tételre épít [6]. Az utóbbinak ráadásul előnye, hogy az algebrai ekvivalenciának és algebrai függetlenségnek a definícióit nem, csak bizonyos tulajdonságaikat használja fel. Ezért Kertész észrevétele szerint hasonlóképpen alkalmazható az ekvivalencia és függetlenség absztrakt változataira, ennek következményeként pedig könnyedén adódnak belőle például csoport- és gyűrűelméleti eredmények is [5].
Nagy örömünkre a Kertész család tagjai is szép számban megtisztelték rendezvényünket, jelen volt többek között Kertész Andor fia és testvére, Kertész András akadémikus nyelvészprofesszor és Kertész Attila Liszt Ferenc-díjas karnagy.
Az emlékülésről beszámolt az egyetemi M. Tóth Ildikó Sajtóközpont [14] és annak tudósítása alapján a Dehir.hu debreceni hírportál.
A normáltranszverzálisok alaptétele
Némileg meglepő módon Kertész Andor első cikkeinek egyike geometriai témával, a normáltranszverzálisokkal foglalkozik [11]. Elemi eszköztára, könnyen érthetősége és rövidsége miatt ezt be is tudjuk az alábbiakban mutatni.
Jól ismert, hogy a háromdimenziós euklideszi tér két kitérő egyenese esetén egy és csak egy olyan egyenes létezik, amely mindkettőt merőlegesen metszi, ezt nevezzük a normáltranszverzálisuknak. Továbbá a két kitérő egyenes legközelebbi pontjai a normáltranszverzálisukkal vett metszéspontok.
Ez a tétel belátható akár tiszta geometriai eszközökkel,2 itt azonban vektorok segítségével szeretnénk igazolni. Kertész Andor és Szele Tibor több analitikus geometriai könyv átnézése során azt tapasztalták, hogy a minimális távolságról szóló résznél általában a kétváltozós függvények szélsőérték-számítására van szükség,3 amivel viszont a bevezető fejezetekkel ismerkedők még jellemzően nem találkoztak. Ezért az volt a céljuk, hogy olyan bizonyítást adjanak, amely csak elemi eszközöket használ a vektoralgebrából.
Adjuk meg a két kitérő egyenest paraméteresen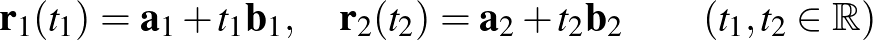 alakban, ahol
alakban, ahol 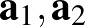 a két egyenes egy-egy pontjának helyvektora,
a két egyenes egy-egy pontjának helyvektora, 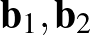 az irányvektoraik. Mivel az egyenesek kitérők, ezért
az irányvektoraik. Mivel az egyenesek kitérők, ezért 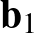 és
és 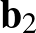 nem párhuzamosak, következésképpen létezik olyan
nem párhuzamosak, következésképpen létezik olyan 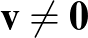 vektor, amely merőleges
vektor, amely merőleges 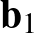 -re és
-re és 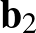 -re is,
-re is, 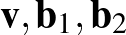 pedig bázist alkotnak.
pedig bázist alkotnak.
Az első egyenes 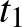 és a második egyenes
és a második egyenes 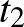 paraméterű pontját összekötő egyenes akkor és csak akkor merőleges mindkét egyenesre, ha
paraméterű pontját összekötő egyenes akkor és csak akkor merőleges mindkét egyenesre, ha 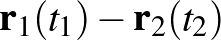 merőleges
merőleges 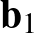 -re és
-re és 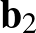 -re, azaz valamilyen
-re, azaz valamilyen 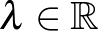 mellett
mellett 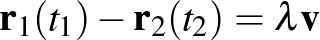 . Ez ekvivalens az
. Ez ekvivalens az 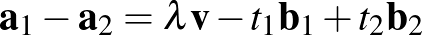 egyenlőséggel, ilyen
egyenlőséggel, ilyen 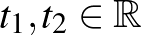 pedig pontosan egy létezik tekintettel arra, hogy
pedig pontosan egy létezik tekintettel arra, hogy 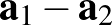 egyértelműen áll elő a bázisvektorok lineáris kombinációjaként.
egyértelműen áll elő a bázisvektorok lineáris kombinációjaként.
A második rész igazolásához speciálisan válasszuk 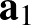 -et és
-et és 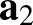 -t a normáltranszverzálissal vett metszéspontokba mutató helyvektoroknak. Ekkor
-t a normáltranszverzálissal vett metszéspontokba mutató helyvektoroknak. Ekkor 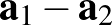 merőleges
merőleges 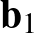 -re és
-re és 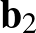 -re, így az egyenesek tetszőleges pontjainak távolságnégyzete a Pitagorasz-tétel alapján
-re, így az egyenesek tetszőleges pontjainak távolságnégyzete a Pitagorasz-tétel alapján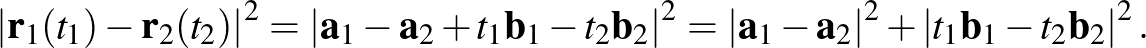 Ebből azonnal leolvasható, hogy a távolság
Ebből azonnal leolvasható, hogy a távolság 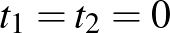 esetén veszi fel a legkisebb értékét.
esetén veszi fel a legkisebb értékét.
Nyul Gábor,
Debreceni Egyetem, Matematikai Intézet
Hivatkozásjegyzék
- [1] Erinnerungen an Andor Kertész (1929–1974), Georg Cantor Heft, Sonderheft 2010.
[2] K. Győry, Andor Kertész 1929–1974, Publicationes Mathematicae Debrecen 21 (1974), 159–160.
[3] A. Hajnal and A. Kertész, Some new algebraic equivalents of the Axiom of Choice, Publicationes Mathematicae Debrecen 19 (1972), 339–340.
[4] A. Kertész, Simple proof of a fundamental theorem of field theory, American Mathematical Monthly 66 (1959), 804.
[5] A. Kertész, On independent sets of elements in algebra, Acta Scientiarum Mathematicarum 21 (1960), 260–269.
[6] Kertész A., Egyszerű bizonyítás Steinitz egy tételére, Matematikai Lapok 12 (1961), 32–37.
[7] A. Kertész, Die Bedeutung der Cantorschen Gedanken für die Entwicklung der Algebra, Scientia 105 (1970), 685–693. (Angol változat: A. Kertész, The significance of Cantor's ideas for the development of algebra, Scientia 105/Suppl. (1970), 203–209.)
[8] Kertész A., Száz éves a valós számok egzakt bevezetése, Matematikai Lapok 22 (1971), 231–233. (Német változat: A. Kertész, Hundert Jahre exakte Einführung der reellen Zahlen, Nova Acta Leopoldina 38 (1973), 455–457.)
[9] A. Kertész, Einführung in die transfinite Algebra, Akadémiai Kiadó, 1975.
[10] A. Kertész (bearbeitet von M. Stern), Georg Cantor 1845–1918: Schöpfer der Mengenlehre, Acta Historica Leopoldina Nr. 15, Deutsche Akademie der Naturforscher Leopoldina, 1983.
[11] A. Kertész and T. Szele, On the smallest distance of two lines in 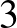 -space, Publicationes Mathematicae Debrecen 2 (1951–1952), 308–309.
-space, Publicationes Mathematicae Debrecen 2 (1951–1952), 308–309.
[12] L. Rédei, O. Steinfeld und R. Wiegandt, Die wissenschaftliche Tätigkeit von Andor Kertész, Publicationes Mathematicae Debrecen 23 (1976), 1–9.
[13] In: Vincze Cs. (szerkesztő), Mathesis necesse est: 100 éves a matematika oktatása a Debreceni Egyetemen, Debreceni Egyetemi Kiadó, 2024, 276–278.
[14] A kiváló matematikusra emlékeztek, Debreceni Egyetem M. Tóth Ildikó Sajtóközpont. https://hirek.unideb.hu/kivalo-matematikusra-emlekeztek
Lábjegyzetek
- 1 A tételben szereplő fogalmak definíciói:
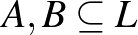 algebrailag ekvivalensek
algebrailag ekvivalensek 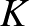 felett, ha
felett, ha 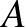 minden eleme algebrai
minden eleme algebrai 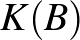 felett és
felett és 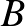 minden eleme algebrai
minden eleme algebrai 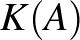 felett.
felett. 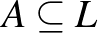 algebrailag független
algebrailag független 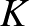 felett, ha bármely
felett, ha bármely 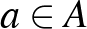 elem transzcendens
elem transzcendens 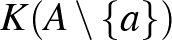 felett.
felett. - 2 Ld. például: Hajós Gy., Bevezetés a geometriába, Nemzeti Tankönyvkiadó, 1995, 193–194.
- 3 Ld. például: R. Rothe, Höhere Mathematik für Mathematiker, Physiker, Ingenieure. Teil II, B. G. Teubner Verlagsgesellschaft, 1951, 191–192.











