A Beke Manó Emlékdíjakat nem tudták átadni a 2020-ban elmaradt Rátz László Vándorgyűlésen, ezért került sor decemberben az eseményre.
A Beke Manó Nagydíjat Pelikán József kapta.
Pelikán József a legendás, első specmatos osztályba járt. A "Ki miben tudós" televíziós vetélkedő révén már középiskolás korában országosan ismert lett a neve. A Nemzetközi Matematikai Diákolimpián, háromszor arany, egyszer ezüstérmet szerzett. Két megoldása is különdíjat kapott. Talán ez indította arra, hogy később, komoly matematikusként vállalja az Diákolimpiákon induló magyar csapat vezetését. Egy emberöltőn keresztül, összesen 31 alkalommal volt a csapat vezetője. A Keszthelyen rendezett olimpia univerzális jolly-jokereként szinte minden fajta feladatot végzett. A Diákolimpiák szervezését irányító nemzetközi testületnek sok éven át tagja, két cikluson át – azaz 8 éven keresztül – elnöke volt. Munkáját 2014-ben Erdős-díjjal ismerték el. A tavalyi, 60. Nemzetközi Matematikai Diákolimpia után bejelentette visszavonulását és egyúttal az utódját is kiszemelte, és a feladatra felkészítette.
Az olimpiai munka mellett a diákolimpiai csapat felkészítésében is rendszeresen segített, előadásokat tartott. A 2000-es évek elején közös magyar-román edzőtábort szervezett és ennek fő előadója volt öt éven át. A Reiman István által koordinált Ifjúsági Matematika Kör alkalmain, és a húsz éves múltra visszatekintő angol-magyar olimpiai edzőtáborban szinte minden évben tartott előadást. A diákok matematikai tartalom és előadói stílus tekintetében is a legmagasabb osztályzattal értékelték visszajelzéseikben előadásait.
Beke Manó Emlékdíjat kapott Mihályi Gyula, Kimle Mária és Dr. Rókáné Rózsa Anikó.
Mihályi Gyula 1980 óta tanít a székesfehérvári Teleki Blanka Gimnáziumban. Tevékenyen részt vett a speciális matematika oktatás megszervezésében. A matematika tagozat fenntartását, megújítását ma is szívügyének tartja. Iskolájában dolgozott igazgatóként, igazgatóhelyettesként és a matematika munkaközösség vezetőjeként.
Szaktanárként magas színvonalú oktató-nevelő munkát folytat, és osztályfőnöki tevékenységét is ugyanilyen módon, lelkiismeretesen végezte. Tanítványai az élet minden területén megállják a helyüket, és sokan értek el közülük kimagasló szakmai sikereket. Mindig is nagy figyelmet szentelt a tehetséggondozásnak, és emellett természetesen a felzárkóztatásra is gondot fordított. Több tanítványa ért el szép eredményeket az Arany Dániel versenyeken és az OKTV-n. Diákjai közül többen indulnak a Középiskolai Matematikai és Fizikai Lapok pontversenyében.
Évek óta tagja az OKTV matematika versenybizottságának és az Abacus matematikai lapok felügyelőbizottságának. Tartott bemutató órát a speciális matematika tagozatos osztályokban tanító tanárok szakmai-módszertani továbbképzésén. Széleskörű tapasztalatát, meglátásait szívesen osztja meg kollégáival. Segítőkész módon karolja fel a pályakezdő fiatalokat. Kiemelkedő szakmai felkészültségű munkáját alaposság és precizitás jellemzi. Elhivatottságával, szakmai felkészültségével és emberségével méltán vívta ki kollégái és tanítványai megbecsülését.
Kimle Mária hosszú évek óta dolgozik a matematikai tehetséggondozásban. Az általános iskolás és a középiskolás korosztály tehetségfejlesztésében egyaránt jártas. Diákjai szép eredménnyel szerepeltek a Varga Tamás Matematika Versenyen, a Nemzetközi Magyar Matematikaversenyen, az Arany Dániel Matematikaversenyen és az OKTV-n. Tanítványait arra ösztönzi, hogy rendszeresen oldják meg és küldjék be a KöMaL feladatait, amiket szakköri munkájában is felhasznál. Sok tanulót készített fel eredményesen a műszaki és a természettudományos pályákra. Rendszeres szervezője iskolája matematika táborainak, szervezői munkáját pontosan, nagy odadással végzi. Középiskolára felkészítő szakköröket és megyei matematika szakköröket szervez.
Szaktanári munkáját a precizitás és a strukturáltság jellemzi, gondosan ügyel a legapróbb részletekre is. Diákjait megtanítja arra, hogy bármely területen tanulnak, dolgoznak, a precíz munkával nem csak saját munkájukat könnyítik meg, hanem közelebb jutnak céljaik megvalósításához. Mindezt humorral oldott légkörben éri el.
Dr. Rókáné Rózsa Anikó iskolájában a matematika munkaközösség szakmai életének kiváló vezetője. A szakmai pályázatokat aktívan segíti. Koordinálja az iskolai versenyeket, népszerűsítő programokat, segít azok megvalósításában. Aktív segítője a továbbtanulást segítő programoknak is, pl. SZTE Kutatók éjszakája, BME Nyitott laborok délutánja. Szívesen tart bemutató órákat, oszt meg jó gyakorlatokat, mentorál pályakezdőket és tapasztalt kollégákat is. Szakmailag nagyon jól képzett, felkészült tanár. Önmagával és tanítványaival szemben is igényes, megköveteli a komoly, rendszeres munkát, ugyanakkor kellő megértéssel rendelkezik diákjai iránt. Tanítását igényesség és sokszínűség jellemzi. Rendszeresen részt vesz szakmai továbbképzéseken, változatos módszerek alkalmazásával színesíti tanóráit.
A népszerűsítő munka mellett nagyon nagy hangsúlyt fektet a tehetségek gondozására, kiváló versenyeredményei vannak. Munkájában felhasználja és népszerűsíti a szakmai folyóiratokat, leginkább a KöMaL-t és az ABACUS-t. Diákjai rendszeresen oldanak meg feladatokat tanítási órákon és tehetséggondozó foglalkozásokon.
Szaktanácsadó munkájának kapcsán Békés megye matematikatanításának meghatározó személyisége. Aktív szervezője a megyei, sőt országos szintű Mesterek és tanítványaik programsorozatnak, a Békéscsabai Középiskolai Matematikaverseny szervező csapatának egyik vezető személyisége. Az általános iskolák 8. osztályos tanulóinak meghirdetett, egész Békés megyére kiterjedő Horváth János Matematikaverseny főszervezője. Szoros kapcsolatokat ápol az egyetemekkel, segíti azok megjelenését iskolájában, diákokat irányít, segít, hogy eljussanak az egyetemi előkészítő programokra. Népszerűsítő és tehetséggondozó munkájának eredménye, hogy iskolájából nagyon sokan választják a matematikát továbbtanuló tantárgyként. Ezzel sokat segít a matematika, általában a természettudományok népszerűsítésében.
Szele Tibor Emlékérem: Hajnal Péter
A 2020. évi Szele Tibor Emlékérmet a Bizottság (Babai László, Hatvani László, Krisztin Tibor, Pete Gábor, T. Sós Vera, Simonovits Miklós, Totik Vilmos és Tóth Bálint) Hajnal Péternek, a Szegedi Tudományegyetem Bolyai Intézetének habilitált tanszékvezető docensének ítélte. Hajnal Péter nagyszerű matematikai ízléssel és odaadással végzi kutatásait és a fiatalok mentorálását.
A szegedi Bolyai Intézetben diplomázott 1984-ben Lovász László témavezetésével, ezután a University of Chicago Számítástudományi Tanszékén szerzett doktori fokozatot 1988-ban Simon János és Babai László diákjaként Complexity of Graph Problems című disszertációjával. Pár éves MIT és princetoni posztdoktori állások után 1990-ben tért vissza a Bolyai Intézetbe, ahol 2006-ban habilitált. Ő vezeti a Halmazelméleti és Matematikai Logikai Tanszéket, korábban intézetvezető-helyettes volt. Jelenleg az intézet doktori iskolájának helyettes vezetője. Számos OTKA-pályázat nyertese és a zsűri visszatérő tagja. Hivatalosan 6 PhD disszertáció témavezetője volt eddig, de a valóságban ennél jóval több fiatalt indított el kutatói pályáján. Több évtizede szervezi lankadatlan energiával a szegedi Kombinatorika Szemináriumot, és ez a szeminárium a fiatal tehetségeknek mindvégig valódi kibontakozási lehetőséget biztosított.
A kombinatorika és gráfelmélet területén dolgozik, 35-nél több dolgozatára 300 fölötti független hivatkozás érkezett. Legnagyobb hatású munkája a Füredi Zoltánnal közös Davenport–Schinzel theory of matrices (1992), melyben az extremális gráfelmélet egy rendezett változatát vezetik be: egy 0-1 mátrixban legfeljebb hány 1-es lehet, hogy egy adott részmátrix ne forduljon elő. Amikor ez a részmátrix egy tetszőleges permutációmátrix, a megengedhető szám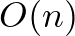 
: ez volt a híres Füredi-Hajnal sejtés, melyet bizonyos esetekben már az eredeti cikk bizonyított, és amit végül teljes egészében, a Stanley-Wilf sejtéssel együtt, Adam Marcus és Tardos Gábor igazolt 2004-ben.
Egy izgalmas bonyolultságelméleti eredménye a következő. Rivest és Vuillemin 1975-ben bizonyították, hogy tetszőleges monoton tranzitív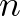 
-változós Boole-függvény kiszámolásához, legalábbis ha 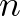egy prímhatvány, a legrosszabb input esetén meg kell kérdezni 
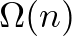bitet, és ebből igazolták, hogy tetszőleges 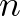-re, tetszőleges monoton gráf-tulajdonság ellenőrzéséhez 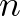csúcson legalább 
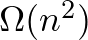élet meg kell kérdezni. Ha az algoritmus véletlent is használhat, akkor vannak monoton tranzitív Boole-függvények, melyekre 
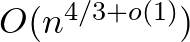kérdés is elég, ám Karp és Yao egymástól függetlenül azt sejtették (1977), hogy monoton gráftulajdonságnál továbbra is szükséges 
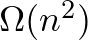kérdés. A legjobb ismert kitevő 
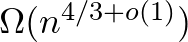, melyet először Hajnal Péter igazolt 1991-ben, egy gráfpakolási lemma segítségével. Azóta ezt az alsó korlátot O'Donnell, Saks, Schramm, és Servedio (2005) bebizonyította általános monoton tranzitív Boole-függvényekre is (ahol ez éles), teljesen más módszerrel, diszkrét Fourier-analízist használva.
Az általa több évtizede szervezett Kombinatorika Szeminárium a szegedi matematikai élet egyik fontos helyszíne, amely sok szállal kapcsolódik a szegedi informatikusok kutatásaihoz (olyan állandó informatikus résztvevőkkel, mint Pluhár András, Csaba Béla, vagy a fiatalon elhunyt Imreh Csanád.) A szeminárium a kombinatorikát a legtágabban értelmezi, melybe a bonyolultságelmélettől kezdve a geometrián és a csoportelméleten keresztül a statisztikus fizikáig minden belefér. A kombinatorika iránt érdeklődő szegedi fiatalok több generációja itt tanult meg cikkeket olvasni és előadni, előadásokat kritikusan hallgatni, új kérdéseket feltenni, kutatóvá válni.
Hajnal Péter témavezetésének legfőbb jellemzője az, hogy a diákot rávezesse arra, mi érdekli őt igazán – soha nem akarja a saját érdeklődését ráerőltetni a diákra. Azt bátorítja, hogy a diák ott szerezzen fokozatot, ahol a világon az adott téma erős, ahol a legtöbbet tanulhat. OTKA pályázatai költégeinek jelentős hányadát fordította arra, hogy a diákok konfenciákon, nyári iskolákon vehessenek részt. A Hajnal Péterrel való matematikai interakció személyes élményét kiegészítik nagyszerű tankönyvei, feladatgyűjteménye, ismeretterjesztő cikkei. Ezek közül kiemeljük a következő könyveket, amelyeken hallgatók generációi nőttek fel: Elemi kombinatorikai feladatok, Gráfelmélet, Algoritmuselmélet és bonyolultságelmélet, Diszkrét matematika, Halmazrendszerek.
Eddig 6 PhD diákja volt. Barát János 2002-ben védte meg disszertációját gráfelméletből, jelenleg a Pannónia Egyetem docense, a Rényi Intézet vendégkutatója. Balogh József (2003), aki kész PhD disszertációval rendelkezett Hajnal Péter vezetésével, mielőtt további tanulmányokra Memphisbe utazott, ahol hivatalos PhD-jét megszerezte. Jelenleg Urbana-Champaignben professzor, az extremális kombinatorika egyik vezető kutatója, maga is tíznél több PhD diák témavezetője .Nagy-György Judit (2010) Imreh Csanáddal közös diákja volt, disszertációját online algoritmusokból írta. A Bolyai Intézet Sztochasztika Tanszékének docense. Mészáros Viola (2011) Pavel Valtrral (Prágai Károly Egyetem) volt közös diákja, disszertációját kombinatorikus geometriából írta. Prágában, a TU Berlinen, és a Lausanne-i EPFL-en volt posztdoktor, jelenleg Berlinben él. Nagy V. Gábor (2014) a Catalan-számokhoz kapcsolódó bijekciókból irta PhD-jét, jelenleg a Bolyai Intézet Halmazelméleti és Matematikai Logikai Tanszékének adjunktusa. Bényi Beáta (2015) a poly-Bernoulli számokhoz kapcsolódó bijekciókból irta disszertációját, jelenleg a Nemzeti Közszolgálati Egyetem főiskolai docense.
MSc diákjainak száma 30, közülük sokan jelentős kutatókká váltak. Ők ugyan doktori fokozatukat nem Szegeden szerezték, de Hajnal Péter óriási hatással volt matematikai ízlésükre, fejlődésükre, stílusukra. Pete Gábor a Rollo Davidson (2011) és az Erdős Pál (2014) díjak nyertese, jelenleg a Rényi Intézetben az ERC Zajérzékenység Kutatócsoport vezetője, és a BME Sztochasztika Tanszék docense. Timár Ádám a Rényi Intézet és a University of Iceland kutatója.
A Grünwald Géza Emlékérem jogelődjét, a Grünwald Géza Emlékdíjat a Bolyai János Matematikai Társulat 1951-ben alapította a matematikai alapkutatásban kiemelkedő tudományos eredményeket elérő, fiatal magyar matematikusok jutalmazására. 2018-ban a Társulat a jutalmazhatók körét kiterjesztette a Magyarországon tanulmányokat folytatott külföldi kutatókra is.
2020-ban a Grünwald Géza Emlékéremre négy felterjesztés érkezett, egyikőjüket viszont a jelenleg érvényes szabályok szerint a Bizottságnak nem állt módjában kitüntetni. Egyhangú döntéssel, a Bizottság idén két díjazottat szavazott meg:
Grünwald Géza emlékérmet kapott 2020-ban Gyenizse Gergő és Tomon István.
Gyenizse Gergő 1991-ben született. Matematikus alap-, majd mesterszakos tanulmányait 2007 és 2013 között végezte a Szegedi Tudományegyetemen, majd ugyanitt folytatta a doktori képzést. Doktori fokozatát 2018-ban szerezte meg, jelenleg pedig a SZTE Bolyai Intézet adjunktusa.
Gyenizse Gergőnek 8 cikke jelent meg, melyek közül két munka egyszerzős. Főleg az univerzális algebra területén folytat kutatásokat. A téma egyik nélkülözhetetlen eszköze a szelíd kongruenciák 1988-ban bevezetett elmélete, mely segítségével sok tétel érvényességi határát sikerült pontosan meghatározni, illetve számos sejtést igazolni. Gyenizse Gergő eddig legnagyobb eredménye a szelíd kongruenciák elméletének kiterjesztése algebrák kompatibilis kvázirendezés-hálóira, mely segítségével társszerzőivel egy 1984 óta nyitott problémára adott nemleges választ. Ezen kívül vizsgálta irányított gráfok transzformációgráfjainak algebrai tulajdonságait is, amely szorosan kapcsolódik a constraint satisfaction problem algoritmikus komplexitásának vizsgálatához. Több hálóelméleti eredménnyel is rendelkezik. Többek között társszerzőivel megmutatta, hogy a megszámlálhatóan végtelen elem által generált szabad háló beágyazható a 3-elem által generált szabad háló szimmetrikus elemei által alkotott részhálójába.
Tomon István 1990-ben született. BSc és MSc diplomáit az ELTE matematikus szakán szerezte kitűnő eredménnyel, aztán a Cambridge-i Trinity College-ba került, ahol 2016-ban Bollobás Béla iányításával szerzett doktori címet. Ezután Lausanne-ban, az EPFL-en töltött három évet posztdoktorként Pach János csoportjában, jelenleg pedig a zürichi ETH-n dolgozik Benny Sudakov csoportjában posztdoktorként.
Tomon Istvánnak eddig 24 dolgozata jelent meg nemzetközi folyóiratokban, s további 10 áll megjelenés alatt. Nehéz, sokak által vizsgált kombinatorikai kérdésekre összpontosít, cikkei a legszínvonalasabb folyóiratokban jelennek meg. Eredményei közül csak párat emelünk ki. Sikerült belátnia, hogy az összefüggő síkbeli görbék metszetgráfjaira (az úgynevezett string-gráfokra) teljesül az Erdős-Hajnal sejtés, amely a Ramsey-elmélet egyik legfontosabb nyitott problémája. Egy másik, extremális gráfelmélethez tartozó eredménye egy n csúcsú, r-uniform, körmentes hipergráf maximális élszámának becslése, itt Sudakovval együtt aszimptotikusan közel optimális felső korlátot sikerült bizonyítaniuk. Erdős, Faudree és Sós egy régi kérdését válaszolta meg azzal, hogy társszerzőivel együtt megmutatta, egy n csúcsú C-Ramsey gráfnak legalább n2-o(1) különböző élszámú részgráfja van. Egy híres, részbenrendezett halmazokra vonatkozó pakolási problémát is vizsgált: megmutatta, hogy egy n elemű halmaz részhalmazainak hálója pontosan akkor parkettázható ki egy P részbenrendezett halmaz példányaival, ha P elemszáma 2-hatvány, és P-nek van egy egyértelmű minimuma és maximuma. Egy további, részbenrendezett halmazokra vonatkozó eredményében pedig belátta, hogy egy rögzített alaphalmazon definiált összefüggő gráfoknak a részgráf tulajdonság által parciálisan rendezett halmaza rendelkezik a Sperner tulajdonsággal, azaz legnagyobb antilánca a legnagyobb szint elemeiből áll.
2020-ban Farkas Gyula Emlékdíjat kaptak Berend Gábor, Fekete Imre, Molontay Roland és Rigó Petra Renáta.
A részletes indoklások, amelyeket itt is közzé tettünk, megjelentek az Alkalmazott Matematikai Lapok 37 (2020), 1-2. számában.
2020-ban a Rényi Kató Emlékdíj Bizottság két jelöltnek ítélte oda a Rényi Kató Emlékdíj I. fokozatát: Grünwald Richárdnak és Schwarcz Tamásnak.
Grünwald Richárd a Debreceni Egyetem Matematika- és Számítástudományok Doktori Iskolájának elsőéves doktorandusz hallgatója. Kutatásai során Páles Zsolt témavezetése mellett először valós algebrai derivációkkal foglalkozott. Az eredményeikből készült két dolgozatot az Acta Mathematica Hungarica és a Publicationes Mathematicae Debrecen közölte, illetve fogadta el. Számos magyar- és angol nyelvű előadást is tartott erről a témáról.
Ezt követően figyelme a középértékek elméletében felmerülő kérdések vizsgálata felé fordult. Sikerült megoldaniuk az általánosított Bajraktarević-közepek egyenlőségi problémáját. Az ebből írt dolgozat az Aequationes Mathematicae-ben jelent meg. Az ebben elért eredményekről a 15th International Students' Conference on Analysis nemzetközi konferencián tartott előadást.
Schwarcz Tamás az Eötvös Loránd Tudományegyetem elsőéves doktorandusz hallgatója. Bérczi Kristóf témavezetésével tavaly kezdett el matroidok közös bázisainak pakolásán dolgozni. Rendkívül hatékonyan kombinálja matematikai széleslátását programozási ismereteivel, melynek eredményeképpen sikerült megmutatniuk, hogy egy bizonyos értelemben nehéz két matroid metszetében két diszjunkt közös bázist találni. Ez a probléma régóta nyitott volt, az eredményeket bemutató cikket a tekintélyes Mathematical Programming folyóirat fogadta el.
Yutaro Yamaguchival közösen folytatták vizsgálataikat, melyek elsősorban matroidok redukálhatóságára irányultak. Sikerült megmutatniuk, hogy a kombinatorikus optimalizálásban leggyakrabban előforduló matroidok jól közelíthetőek partíciós matroidokkal. Ennek eredményeképpen felső korlátot adtak két ezen osztályokból kikerülő matroid metszetének listaszínezési számára.
A Bolyai János Matematikai Társulat elnöksége által kiküldött bizottság a Patai Alapítvány 2020. évi díját Fridrik Richárdnak és Kiss Mártonnak ítélte oda.
Kiss Márton 2020 januárjában szerzett matematika-fizika szakos középiskolai tanári diplomát a Debreceni Egyetemen. Jelenleg a jászberényi Szent József Katolikus Elektronikai Technikum, Gimnázium es Kollégiumban tanit matematikát es fizikát. 2020 szeptemberétől a Debreceni Egyetem Matematika es Számitástudományok Doktori Iskola Didaktika programjának nappali tagozatos PhD hallgatója.
Már egyetemi tanulmányai alatt diákköri kutatómunkát végzett a matematika didaktika területén. Dolgozataival szerepelt a XXXIII. es XXXIV. OTDK Tanulás- es Tanitámódszertani −Tudástechnológiai Szekciójában. Jelenleg PhD hallgatóként kutatási témája a problémamegoldás folyamatának elemzéséhez kapcsolódik. Középiskolás tanulók körében vizsgálta a megértés és memória szerepét, valamint a metakognitív tevékenységek fejlesztésének lehetőségeit. Jelenlegi kutatásaival arra keresi a választ, hogy hogyan építhető be a normál tanterv szerint haladó osztályok tananyagába a problémamegoldás, hogyan érhető el, hogy a tanulók aktív részesei legyenek a matematikaóráknak és ezáltal tartós tudásra tegyenek szert. 2016 óta folyamatosan végez felméréseket, 2019 óta pedig tanítási kísérleteket is középiskolai osztályokban. 2017 óta több hazai és nemzetközi konferencián tartott előadást illetve vett részt poszterrel. Két angol és két magyar nyelvű dolgozata jelent meg. Második éve vesz részt a Matematika és Informatika Didaktikai Kutatások (MIDK) elnevezésű, évenként megrendezésre kerülő konferenciasorozat szervezesében.
Fridrik Richárd 2018-ban szerzett matematika- és fizika tanári oklevelet a Szegedi Tudományegyetemen. Jelenleg a hódmezővásárhelyi Eötvös József Technikumban matematikatanár. 2008-tól a Magister Universitas Matematika Szekciójában érettségi felkészítő tanár emelt és közép szinten egyaránt.
2013-tól folyamatosan tart tehetséggondozó szakköröket Szegeden, Pécsen, Komáromban, Bonyhádon, Gyulán és Gödöllőn. Az SZTE, PTE és a BJMT által szervezett szakmai napokon két-két alkalommal is felkérték, hogy népszerűsítő előadásokat tartson az egyetem által szervezett matematikai napokon. A Szabadkai Nyári Egyetem felkérésére 2020. októberben online formában tartott továbbképzést ottani tanároknak „Vizsgáljuk meg kicsiben a problémát!” címmel.
2012 óta folyamatosan minden évben részt vesz és aktívan tevékenykedik a matematikatanárok Rátz László Vándorgyűlésén. Még középiskolásként javasolt feladatokat a Zrínyi Ilona matematikaversenyre, ahol 2008-ban több feladatát is kitűzték. 2017. óta folyamatosan szervező a Dürer Matematika versenyen. Feladatait többször kitűzték a versenyen. 2012-ben ő állította össze a Szőkefalvi-Nagy Gyula matematikai emlékverseny 11. osztályos feladatsorait, valamint javította és értékelte a döntős versenydolgozatokat.
Több feladata megjelent 2009-2010-ben a Matematika Tanítása folyóiratban, tanároknak szóló versenypéldaként. 2018 óta Ratkó Éva főszerkesztő felkérésére folyamatosan készít matematika emelt szintű gyakorló feladatsorokat a KöMaL számára. Hamarosan megjelenik két előadásából készült cikke a szlovákiai Katedra folyóiratban.
A Bod Péter Emlékdíj célja a társadalombiztosítás, illetőleg a nyugdíjrendszerek szakmailag megalapozott, igényes aktuáriusi megközelítésű vizsgálatának, modellezésének, az elméleti modellek tényleges gyakorlati alkalmazásának elősegítése a fiatal magyar szakemberek körében, ily módon hozzájárulva az e rendszerek egyre szakszerűbb működéséhez szükséges tudományos és gyakorlati munka megalapozásához, ezáltal a közérdek kiteljesedéséhez. E vonatkozásban a nyugdíjrendszer fogalma tágan értelmezve magában foglal minden, az időskor biztonságát, az időskori ellátást segítő formát, így magát a szűkebben értelmezett társadalombiztosítást, a kötelező, önkéntes és foglalkoztatói nyugdíjpénztárakat, az ilyen célú biztosításokat vagy más nyugdíjcélú megtakarításokat. Az e célokkal összhangban − fiatal kutató által − elvégzett és a Bod Péter Emlékdíjbizottság, illetve a bírálók számára nyilvános és dokumentált teljesítmény díjazható. A hangsúly az alkalmazáson, a gyakorlati hasznosuláson van. Az Emlékdíjra a felhívás minden páros évben kerül kiadásra. Az Emlékdíj alapítói Bod Judit és Lippner György.
A Bod Péter Emlékdíjat Burka Dávidnak, a Budapesti Corvinus Egyetem Számítástudományi Tanszékének adjunktusának ítélte oda az idei évben az Emlékdíjbizottság.
Kutatásának középpontjában a demográfia- és nyugdíjkutatás áll. Burka Dávid doktori kutatása során szimulációs keretrendszer fejlesztett ki, amely lehetőséget biztosít mikroszimulációs nyugdíjmodellek gyors, hatékony és fejlesztői ismereteket nem igénylő implementálásához. Kutatási eredményeit több publikációban ismertette.
A szimulációs megközelítés egy viszonylag új technika, amelynek fejlődését a számítógépes kapacitások jelentős bővülése teszi lehetővé. A szimulációs technika olyan vizsgálatokra ad lehetőséget, amelyek analitikusan nem megragadhatók, azonban amelyek mély betekintést nyújtanak egy-egy probléma gyökeréhez, és alkalmazásuk fontos eredményekhez vezetnek. Azonban e technika alkalmazása valóban csak egy technika, amelynek meghajtása komoly alapismeretekre és megfelelő ítélőképességre van szükség. A nyugdíjrendszerek tudományos és gyakorlatban is alkalmazható elemzése területén e technikai alkalmazása ma már szinte megkerülhetetlen.
Burka Dávid doktori kutatása mellett részt vett a „Fenntartható, intelligens és befogadó regionális és városi modellek” kutatási projektben is, ahol a halandóság modellezésével foglalkozott. Az itt végzett kutatásaiból szintén több publikációja jelent meg.