Több mint 70 évvel ezelőtt a mesterséges intelligencia (MI) kutatásának élvonalában járó tudósok forradalmian új módszerként bevezették a neuronhálózatokat, amelyekkel agyunk működését értelmezhetjük. Az emberi agyban neuronok milliárdjainak összefüggő hálózata értelmezi és dolgozza föl az érzékszerveinkből érkező adatokat, lehetővé téve számunkra, hogy tapasztalatainkból tanulhassunk. A mesterséges neuronhálózatok összefüggő rétegeik segítségével képesek hatalmas mennyiségű adat átszűrésére, ezáltal előre jeleznek és felismernek mintázatokat, követve azokat a szabályokat, amelyeket önmaguknak tanítottak meg.
Mostanra az emberek a neuronhálózatokat egyfajta MI-csodaszerként kezelik, amelyek képesek megoldani mintafelismerési problémaként átfogalmazható technikai kihívásokat. Természetes hangzású nyelvi fordítást nyújtanak. Képkezelő alkalmazások használják őket arra, hogy felismerjék és csoportosítsák a többször felbukkanó arcokat a galériádban. Továbbá a neuronhálózatokon alapuló programok legyőzték a világ legjobb játékosait többek között góban és sakkban.
Mindazonáltal a neuronhálózatok mindig is lemaradtak egy szembetűnő területen: a bonyolult szimbolikus matematikai problémák megoldásában. Ezek között értendőek az analízis kurzusok alapvető elemei, mint az integrálok vagy a közönséges differenciálegyenletek. A bonyodalom magából a precíz megoldásokat követelő matematika jellegéből adódik. A neuronhálózatok ehelyett inkább a valószínűségekben jeleskednek. Megtanulják, hogyan ismerjenek fel mintázatokat – melyik spanyol fordítás hangzik a legjobban, vagy például hogyan néz ki az arcod – és képesek újakat készíteni.
A helyzet az előző év végén változott meg, amikor Guillaume Lample és François Charton, a Facebook párizsi MI kutatócsoportjában dolgozó két informatikus egy új, sikeres megközelítéssel állt elő a szimbolikus matematikai problémák neuronhálózattal történő megoldására. A módszerük nem tartalmazott numerikus közelítéseket, és nem támaszkodott a puszta gépi erőre. Ehelyett kihasználták a neuronhálózatok erősségét; újraértelmezték a matek feladatokat egy tulajdonképpen már megoldott problémaként: ez pedig a nyelvi fordítás.
Kutatásuk eredményeként Lample és Charton programja pontosan ki tudott számítani bonyolult integrálokat és precíz megoldásokat adott differenciálegyenletekre – többek között azokra is, amelyek zavarba ejtettek más, explicit szabályrendszerrel ellátott népszerű matematikai szoftvercsomagokat.
Az új program kihasználja a neuronhálózatok egyik legfontosabb előnyét: saját implicit szabályok alkotására képesek. A gyakorlatban ez azt jelenti, hogy az alkalmazás nem habozott még a legnehezebb integrálok kiszámolása során sem. Elméletben ez a fajta megközelítés képes lehet olyan rendhagyó „szabályokat” alkotni, amelyek előrelépést hozhatnak olyan – jelenleg ember vagy gép által megoldhatatlan – problémák terén, amilyen például új matematikai bizonyítások felfedezése, vagy magának a neuronhálózat természetének a megértése.
Természetesen ez még nem történt meg. De az világos, hogy a csapatnak sikerült választ találnia arra az évtizedes kérdésre, hogy képes-e az MI szimbolikus matematikai számításokat végezni – és a válasz: igen.
A számítógépek mindig is jók voltak nagy mennyiségű számadat feldolgozásában. A matematikai programcsomagok vagy számítógépes algebrai rendszerek több tucat vagy több száz algoritmust kombinálnak, melyek mind be vannak huzalozva előre beállított utasításokkal. Ezek tipikusan szigorúan szabálykövetők, egy-egy adott művelet elvégzésére készültek, viszont nem képesek kezelni a kivételeket. Számos szimbolikus problémára numerikus megoldást adnak, amelyek a mérnöki és fizikai alkalmazásokhoz elegendően pontosak.
A neuronhálózatok másfélék. Nem tartalmaznak behuzalozott (előre beprogramozott) szabályokat. Helyettük nagy méretű tanító mintán gyakorolnak – minél nagyobb, annál jobb – és statisztika segítségével adnak nagyon jó közelítéseket. A folyamat során megtanulják, mi eredményezi a legjobb kimenetelt. A nyelvi fordító programok kifejezetten jeleskednek: ahelyett, hogy szóról-szóra fordítanának, a mondatok értelmét keresik meg a teljes szöveg kontextusát figyelembe véve. A Facebook kutatói a hátrány helyett ebben azt az előnyt látták meg, mely segíthet a szimbolikus matematikai problémák megoldásában. Ez egyfajta problémamegoldási szabadságot ad a programnak.
Ez a szabadság különösen hasznos bizonyos nyitott kérdések esetében, mint például az integrálás. Egy függvény deriváltjának meghatározásához csak néhány előre definiált lépést kell követni. Viszont egy integrál kiszámíításához gyakran valami egyébre is szükség van: valamire, ami közelebb áll a megérzéshez, mint a számoláshoz.
A Facebook-csapat azt gyanította, hogy ezt a megérzést lehetne közelíteni mintafelismeréssel: „az integrálás egyike a mintázat felismerésre leginkább hasonlító matematikai feladatoknak” – állítja Charton. Tehát annak ellenére, hogy a neuronhálózat még nem igazán érti, mit csinálnak a függvények és mit jelentenek a változók, mégis kifejleszt egyfajta ösztönt. A neuronhálózat szépen lassan megérzi, mi az, ami működik, anélkül hogy tudná miért.
Példának okáért ha egy matematikust megkérünk, hogy integrálja pl. az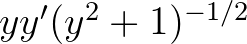 
kifejezést, ösztönösen gyanítani fogja, hogy a primitív függvény – vagyis az a kifejezés, amelynek a fenti a deriváltja – tartalmazni fog valamit, ami hasonlítani fog az 
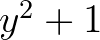négyzetgyökére.
Annak érdekében, hogy a neuronhálózat egy matematikushoz hasonlóan tudja feldolgozni a szimbólumokat, Charton és Lample kezdésképp átültették a matematikai kifejezéseket hasznosabb alakokba. Végül is annál kötöttek ki, hogy fákként értelmezik őket újra – ez lényegében egy mondat ágrajzára hasonlító formátum. Az olyan matematikai műveletek lettek a fa elágazásai, mint például az összeadás, kivonás, szorzás, osztás , hasonlóképpen a hatványozás, vagy a trigonometrikus függvények. Az argumentumok (változók és számok) lettek a levelek. Ez a fastruktúra, néhány kivételtől eltekintve, megragadta azt a módot, amivel a műveleteket hosszabb kifejezésekbe lehet ágyazni.
„Amikor egy terjedelmes függvénnyel találkozunk, látjuk, hogy az kisebb függvényekből áll össze, és van némi megérzésünk azzal kapcsolatban, hogy mi is lehet a megoldás” – mondta Lample. „Úgy gondoljuk, hogy a modell próbál a megoldásra vezető nyomokat keresni a szimbólumokban.” Állítása szerint ezt a folyamatot párhuzamba lehet állítani azzal, ahogyan az emberek oldják meg az integrálokat – és igazából minden más matematikai problémát – azáltal, hogy visszavezetik őket felismerhető alproblémákra, amelyeket már korábban megoldottak.
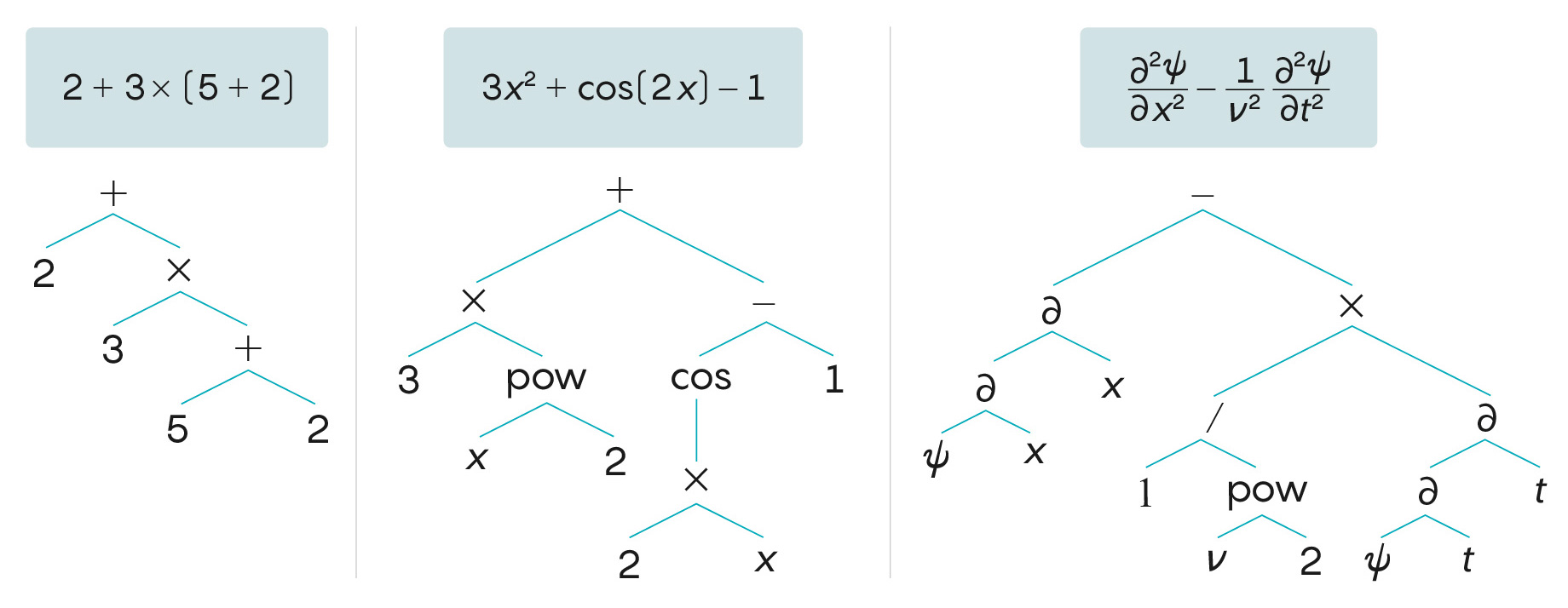
Ennek a struktúrának a kialakítása után a kutatók elemi függvények tömegét használva előállítottak számos tanító mintakészletet – összességében kb. 200 millió (fastruktúrájú) egyenletet és megoldásukat. Ezt követően a mintákat betáplálták a neuronhálózatba, így az megtanulhatta, hogyan néz ki e problémák megoldása.
A betanítás után eljött az ideje, hogy meglássák, mire képes a hálózat. Az informatikusok rábíztak egy 5000 egyenletből álló próbahalmazt, ezúttal megoldások nélkül. (A tesztfeladatok egyike sem volt megoldhatatlan besorolású.) A neuronhálózat diadalmaskodott: sikerült a helyes megoldásokra jutnia – jól és pontosan – a feladatok túlnyomó többségében. Kifejezetten jeleskedett az integrálásban, aminek során a feladatok közel 100%-ában jó megoldásra jutott, ám kevésbé volt eredményes a közönséges differenciálegyenletek terén.
Szinte minden feladat esetében kevesebb, mint 1 másodperc kellett a helyes megoldás előállítására. Sőt, az integrálási példák esetében még az olyan népszerű szoftvercsomagok, mint a Mathematica és a MATLAB egyes megoldóit is felülmúlta gyorsaság és pontosság terén. A Facebook csapata arról számolt be, hogy a neuronhálózat olyan problémákra is megoldást talált, amelyekkel egyik fent említett kereskedelmi megoldóprogram sem boldogult.
A neuronhálózatok használatának további lehetséges iránya az automatikus tételgenerátorok kifejlesztése. A matematikusokat egyre jobban érdekli, hogyan lehet a mesterséges intelligenciát felhasználni új tételek és bizonyítások megalkotására.
Egy másik terület, ahol ez a megközelítés ígéretes lehet, maguknak a neuronhálózatoknak a megismerése: nyugtalanító, de senki sem érti igazán, hogyan is működnek. Tanító bitek lépnek be az egyik oldalon, és jósló bitek bukkannak föl a túloldalon, de hogy a kettő között mi történik – a pontos folyamat, ami miatt ilyen jól jósolnak a neuronhálók –, továbbra is igen fontos nyitott kérdés.
A további érdekességeket tartalmazó cikk teljes egészében a Quanta Magazine 2020. májusi számában olvasható angolul, írója Stephen Ornes.
Az általunk közzétett részleteket fordította: Csuzdi Domonkos (BME), lektorálta: Sugár Tímea (BME).
https://www.quantamagazine.org/symbolic-mathematics-finally-yields-to-neural-networks-20200520/