Beszámoló a 7. fordulóról
Decemberben már hetedik alkalommal közöltünk feladatsort a Héttusa versenyében. Ebben a fordulóban 19-en küldtek válaszokat, megoldásokat, összesen 98 helyes választ.
Öten adtak mind a 7 feladatra hibátlan választ. Itt látható, hogy ki, és melyik feladatot oldotta meg jól.
| A feladat sorszáma | 43. | 44. | 45. | 46. | 47. | 48. | 49. |
| Orangestripes | + | + | + | + | + | + | + |
| Dombi Péter | + | + | + | + | + | + | + |
| S. Ákos | + | + | + | + | + | + | + |
| Fekete Árpád | + | + | + | + | + | + | + |
| Karkó Bálint | + | + | + | + | + | + | + |
| Makay Géza | + | + | + | + | + | + | |
| Bubatov | + | + | + | + | + | + | |
| Ujházy Márton | + | + | + | + | + | + | |
| Turchányi Gyula (Belzebub) | + | + | + | + | + | + | |
| Udvari Tibor | + | + | + | + | + | + | |
| Izsák Beatrix | + | + | + | + | + | + | |
| Szemerédi Ferenc | + | + | + | + | + | + | |
| Berkó Erzsébet | + | + | + | + | + | ||
| D & 2d | + | + | + | + | |||
| Danka Emma (7. oszt.) | + | + | + | ||||
| megérek egy Petákot | + | + | + | ||||
| Keresztvölgyi József | + | + | + | ||||
| Jankó Zsuzsa | + | + | |||||
| Szemerédi Ábris (5. oszt.) | + |
Fordulónként a legjobb megoldók közül néhányan könyvjutalmat kapnak. A legújabb jutalmazottak Berkó Erzsébet és Szemerédi Ferenc, akik az alábbi könyveket választották:
- Paul Erdős and His Mathematics, I-II., Szerkesztette: Halász Gábor, Lovász László, Simonovits Miklós és T. Sós Vera (Bolyai Társulat és Springer Kiadó, 2002)
- Ábrahám Gábor: Egyenlőtlenségek I. (Zalamat Kiadó)
A Héttusába bekapcsolódók számára továbbra érdemes ellátogatni a KöMaL honlapjára további feladatokért és ötletekért, és ajánljuk a Fórum használatát is (https://www.komal.hu/forum?a=to&tid=365). Itt a Héttusa témájában egymással is megbeszélhetik, továbbgondolhatják a problémákat. Lehet beszélgetni, megvitatni félkész ötleteket, felvetődött kérdéseket. A kitűzött feladatokhoz eddig is jöttek különleges, szép megoldások, általánosítások, ezekről – a beküldési határidő után – lehet közösen gondolkodni a Fórum keretei között.
Megoldások, megjegyzések a Héttusa 7. fordulójának feladataihoz
43. Egy egyenesen 14 pont van, 7 kék és 7 piros pont. Lehet-e a pontoknak olyan elrendezése, amikor az azonos színű pontpárok közötti távolságok összege nagyobb, mint a különböző színű pontpárok közötti távolságok összege?
A válasz: Nincs olyan elrendezés.
Megoldás: Legyen az azonos színű pontpárok közötti távolságok összege 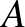 , a különböző színű pontpárok közötti távolságok összege
, a különböző színű pontpárok közötti távolságok összege 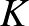 .
.
Legyen 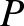 a bal szélső pont, és tőle jobbra az első pont
a bal szélső pont, és tőle jobbra az első pont 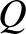 . A két pont távolsága
. A két pont távolsága 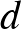 . Ha
. Ha 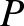 -t eltoljuk
-t eltoljuk 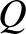 -hoz, az azonos színű pontoktól vett távolságok összege
-hoz, az azonos színű pontoktól vett távolságok összege 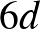 -vel, a különböző színű pontoktól vett távolságok összege pedig
-vel, a különböző színű pontoktól vett távolságok összege pedig 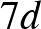 -vel csökken. Ha ez a két, azonos helyen lévő pont különböző színű, akkor töröljük őket. Ekkor
-vel csökken. Ha ez a két, azonos helyen lévő pont különböző színű, akkor töröljük őket. Ekkor 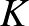 és
és 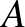 ugyanannyival csökken, és az egyenesen továbbra is ugyanannyi piros és kék pont lesz.
ugyanannyival csökken, és az egyenesen továbbra is ugyanannyi piros és kék pont lesz.
Ezeket a lépéseket ismételjük, amíg eljutunk a jobb szélső pontig. Minden lépésben a bal szélső pontot vagy pontokat toljuk jobbra, a következő pontig. Ez a mozgó blokk azonos színű pontokból áll. Amikor ezt a blokkot mozgatjuk, 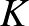 nagyobb mértékben csökken, mint
nagyobb mértékben csökken, mint 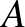 . Ha másik színű pontba ütközik a blokk, akkor kivesszük ezt a pontot és a mozgó blokk egy tetszőleges pontját, azaz elhagyunk egy piros és egy kék pontot. Ha a blokk vele azonos színű ponttal ütközik, akkor ezt a pontot bevesszük a blokkba.
. Ha másik színű pontba ütközik a blokk, akkor kivesszük ezt a pontot és a mozgó blokk egy tetszőleges pontját, azaz elhagyunk egy piros és egy kék pontot. Ha a blokk vele azonos színű ponttal ütközik, akkor ezt a pontot bevesszük a blokkba.
Végül az összes pont eltűnik, így 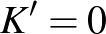 és
és 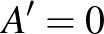 , azaz
, azaz 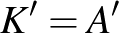 . A lépések során
. A lépések során 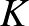 legalább annyival csökkent, mint
legalább annyival csökkent, mint 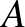 , így kezdetben
, így kezdetben 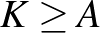 .
.
Ezért nincs olyan konstrukció, amikor 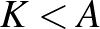 .
.
Fekete Árpád indoklása: A feladatot úgy tudtam megoldani, hogy rájöttem, hogy ha a pontokat egy bal oldali és egy jobb oldali csoportra bontom, akkor ezek a ponthalmazok egymáshoz tolhatók (amíg legalább egy közös pontjuk nem lesz) anélkül, hogy az azonos színű pontpárok közötti távolságok összege jobban csökkenne, mint a különböző színű pontpárok közötti távolságoké. Például, ha egy önálló szélső pontot a többihez húzok, akkor 7 „különböző színű pontpárok közötti” szakasz hosszúsága csökken, míg 6 „azonos színű pontpárok közötti” szakasz hosszúsága csökken (és mind ugyanannyival csökken).
Ezt nagyobb halmazokra kicsit nehezebb belátni, azt kell hozzá tudni, hogy ha 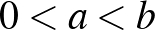 és
és 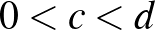 , akkor
, akkor 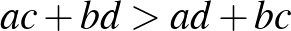 . Szóval, összetolhatjuk az összes pontot egy pontba, és mivel itt az azonos színű pontpárok közötti távolságok összege nem nagyobb, mint a különböző színű pontpárok közötti távolságok összege, ezért az eredeti ponthalmaz esetén sem lesz nagyobb az azonos színű pontpárok közötti távolságok összege.
. Szóval, összetolhatjuk az összes pontot egy pontba, és mivel itt az azonos színű pontpárok közötti távolságok összege nem nagyobb, mint a különböző színű pontpárok közötti távolságok összege, ezért az eredeti ponthalmaz esetén sem lesz nagyobb az azonos színű pontpárok közötti távolságok összege.
Dombi Péter indoklása: Nincs ilyen elrendezés, 7 helyett semmilyen más 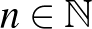 -re sem. Teljes indukcióval bizonyítjuk. Ha
-re sem. Teljes indukcióval bizonyítjuk. Ha 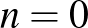 , akkor természetesen igaz, hogy a vegyes távolságok összege nem kisebb, mint az egyszínűek összege:
, akkor természetesen igaz, hogy a vegyes távolságok összege nem kisebb, mint az egyszínűek összege: 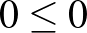 . Legyen
. Legyen 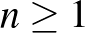 . Ha a piros és kék halmaznak van közös pontja, akkor az egyszerre piros és kék pont elhagyható, hiszen a közös pontnak a többi piros (kék) ponttól való
. Ha a piros és kék halmaznak van közös pontja, akkor az egyszerre piros és kék pont elhagyható, hiszen a közös pontnak a többi piros (kék) ponttól való 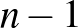 távolsága ugyanúgy szerepel a P-P (K-K) és a vegyes P-K (K-P) összegzésben. Legyen a bal szélső pont
távolsága ugyanúgy szerepel a P-P (K-K) és a vegyes P-K (K-P) összegzésben. Legyen a bal szélső pont 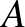 , amiről feltehetjük, hogy piros (ha nem, akkor az összes pontot átszínezzük). Legyen az
, amiről feltehetjük, hogy piros (ha nem, akkor az összes pontot átszínezzük). Legyen az 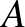 -hoz legközelebbi kék pont
-hoz legközelebbi kék pont 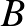 , és legyen az
, és legyen az 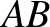 szakaszon a
szakaszon a 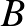 -hez legközelebbi piros pont
-hez legközelebbi piros pont 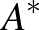 . Mozgassuk el
. Mozgassuk el 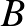 -t balra a
-t balra a 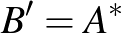 pontba, a többi pont maradjon változatlan. Ekkor az eltolt kék pont a többi
pontba, a többi pont maradjon változatlan. Ekkor az eltolt kék pont a többi 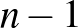 kék ponthoz képest távolodott, összesen
kék ponthoz képest távolodott, összesen 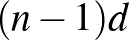 -vel, ahol
-vel, ahol 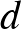 az eltolás mértéke (az
az eltolás mértéke (az 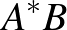 szakasz hossza). Ugyanakkor a piros pontokhoz képest csak a tőle jobbra eső, legfeljebb
szakasz hossza). Ugyanakkor a piros pontokhoz képest csak a tőle jobbra eső, legfeljebb 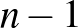 piros ponttól távolodott, mindegyiktől
piros ponttól távolodott, mindegyiktől 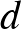 -vel, viszont a piros
-vel, viszont a piros 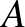 -tól való távolsága rövidült
-tól való távolsága rövidült 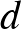 -vel, így a vegyes távolságösszeg csak legfeljebb
-vel, így a vegyes távolságösszeg csak legfeljebb 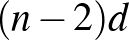 -vel nőhetett. Mivel a piros pontok helyben maradtak, ezért a homogén pontpárok távolságösszege pontosan
-vel nőhetett. Mivel a piros pontok helyben maradtak, ezért a homogén pontpárok távolságösszege pontosan 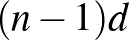 -vel, vagyis a vegyes pontpárokénál többel nőtt. Tehát az
-vel, vagyis a vegyes pontpárokénál többel nőtt. Tehát az 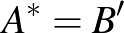 pontot elhagyva az indukciós feltevés és az előrebocsátott megjegyzés értelmében a homogén szakaszok összhossza biztosan nem nagyobb a vegyes szakaszok összhosszánál.
pontot elhagyva az indukciós feltevés és az előrebocsátott megjegyzés értelmében a homogén szakaszok összhossza biztosan nem nagyobb a vegyes szakaszok összhosszánál.
Makay Géza bizonyította azt is, hogy a feladat általánosítható több színre és több pontra, 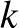 színre és színenként
színre és színenként 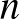 darab pontra.
darab pontra.
44. A zseblámpa 2 ceruzaelemmel működik. Egy dobozban 10 darab – külsőre teljesen egyforma – elem van, 5 új és 5 lemerült. Ezek közül kell 2 jó elemet kiválasztani. Egy próbálkozás során 2 elemet teszünk a zseblámpába, és a lámpa csak akkor fog világítani, ha mindkét elem jó. Van-e olyan, legfeljebb 8 próbálkozásból álló eljárás, amellyel a 10 elemből biztosan rátalálunk 2 jó elemre?
A válasz: Igen, van ilyen eljárás. (Feltételezzük, hogy az új elem mind jó is,)
Megoldás: Osszuk a ceruzaelemeket négy csoportba, ezekből kettőben 3-3, kettőben pedig 2-2 elem legyen. Mindegyik csoportban kipróbáljuk az elempárokat, velük hátha világít a lámpa.
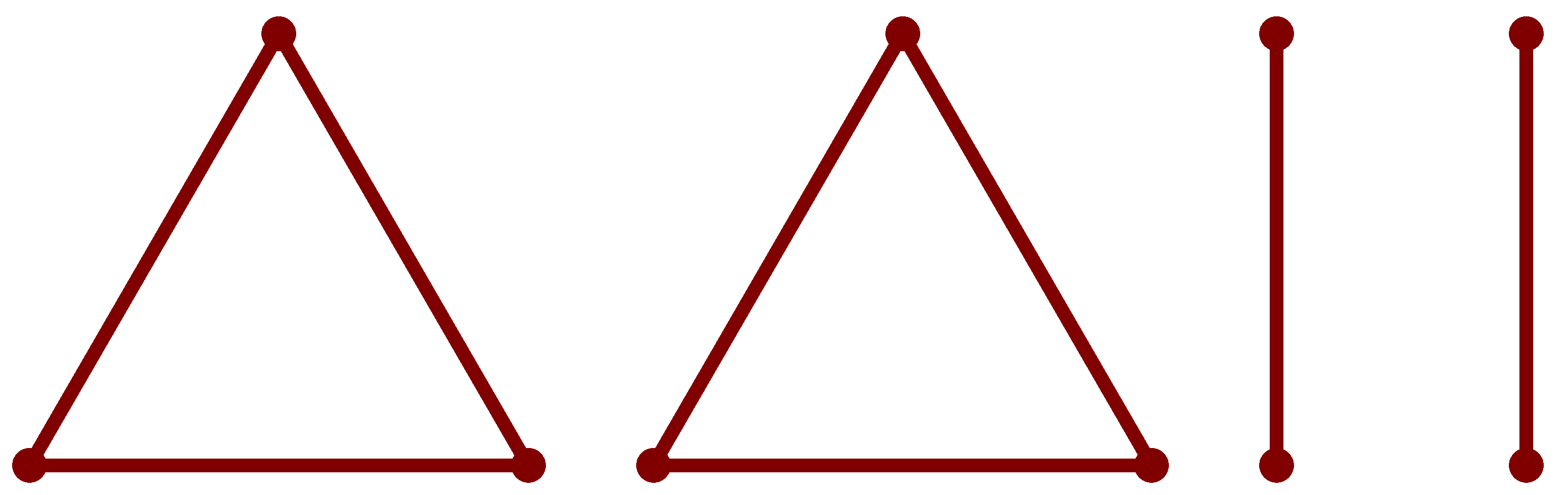
Ez a 3-elemes csoportokban 3 próbálkozást jelent, a 2-elemes csoportokban 1 próbálkozást, ami összesen 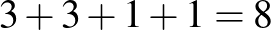 próba.
próba.
Ha a lámpa egyik alkalommal sem világítana, akkor a 3-elemes csoportokban lenne 2-2 rossz elem, és a 2-elemes csoportokban lenne 1-1 rossz elem, azaz legalább 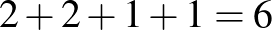 elem lenne rossz, ami ellentmondás. Ezért a 8 próba egyike sikeres lesz, és még az is teljesül, hogy világít a lámpa.
elem lenne rossz, ami ellentmondás. Ezért a 8 próba egyike sikeres lesz, és még az is teljesül, hogy világít a lámpa.
A feladat beéri kevesebbel, elég felmutatni két jó elemet. Ez 7 próbával is elérhető. Ha az előbbi 8 mérésből az első 7 mérés eredménytelen, akkor a nyolcadik mérésre már nincs szükség, mert az utolsó 2-elemes csoportban jók az elemek.
Izsák Beatrix megoldása: Alkossunk 5 párt az elemekből. Ezeket a párokat próbáljuk ki. Ha egyszer sem világított a lámpa, akkor minden párban 1 jó és 1 rossz elem van. Vegyünk kettő párt. Az elsőből válasszuk ki az egyik elemet és próbáljuk ki a másik pár két tagjával. Ha most sem világított, akkor az elsőből vett elem lemerült. A 8. próbálkozás: az első párból a jó elemet kipróbáljuk a másik pár egyik elemével. Ha világít, akkor rendben vagyunk, ha nem, akkor a másik a jó elem, azaz próbálkozás nélkül, de a két elem biztosan jó.
D&2d megoldása: Három csoportba osztjuk a 10 elemet: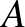 -ban 3 elem,
-ban 3 elem, 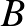 -ben 3 elem,
-ben 3 elem,  -ben 4 elem.
-ben 4 elem.
Az 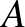 három elempárját ellenőrizzük, amihez legfeljebb háromszor kell mérnünk. Vagy van jó elempár, vagy legfeljebb 1 jó elem van
három elempárját ellenőrizzük, amihez legfeljebb háromszor kell mérnünk. Vagy van jó elempár, vagy legfeljebb 1 jó elem van 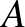 -ban.
-ban.
Ha nem találtunk 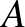 -ban jó elempárt, akkor
-ban jó elempárt, akkor 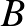 három elempárját ellenőrizzük, amihez legfeljebb háromszor kell mérnünk. Vagy találtunk jó elempárt, vagy legfeljebb 1 jó elem van
három elempárját ellenőrizzük, amihez legfeljebb háromszor kell mérnünk. Vagy találtunk jó elempárt, vagy legfeljebb 1 jó elem van 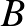 -ben.
-ben.
Ha eddig nem találtunk jó elempárt, akkor hatszor mértünk, és  -ben legalább 3 jó elem van a 4 között.
-ben legalább 3 jó elem van a 4 között.  valamelyik 2 elemét mérjük. Ha jó, rendben, ha nem jó, akkor a másik 2 elem jó. (Valójában a biztonság kedvéért ellenőrizhetjük a két utóbbi elemet, ez a nyolcadik mérés, de már tudjuk, hogy jók lesznek, tehát valójában elég volt a kiválasztáshoz hét mérés.)
valamelyik 2 elemét mérjük. Ha jó, rendben, ha nem jó, akkor a másik 2 elem jó. (Valójában a biztonság kedvéért ellenőrizhetjük a két utóbbi elemet, ez a nyolcadik mérés, de már tudjuk, hogy jók lesznek, tehát valójában elég volt a kiválasztáshoz hét mérés.)
Megjegyzés. Érdemes elolvasni a feladat részletes tárgyalását Pataki János–Meszéna Balázs: A zsebrádiótól Turán tételéig c. cikkében a Fazekas Gimnázium honlapján. (Ott 4 jó és 4 rossz elem között kell 2 jó elemet találni.)
45. Egy 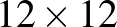 -es táblázat néhány mezőjét elfoglaljuk egy-egy bábu ráhelyezésével. Hány mező lehet foglalt, ha minden mezőnek pontosan egy foglalt szomszédja van? (Két mező szomszédos, ha van közös oldaluk.)
-es táblázat néhány mezőjét elfoglaljuk egy-egy bábu ráhelyezésével. Hány mező lehet foglalt, ha minden mezőnek pontosan egy foglalt szomszédja van? (Két mező szomszédos, ha van közös oldaluk.)
A válasz: 42.
Megoldás: Belátjuk, hogy a táblázat szélső mezőinek fele foglalt, és ezek között van két sarokmező.
Nézzünk egy páratlan sok mezőből álló átlós sort (átlót). Mindegyik mezőnek pontosan egy foglalt szomszédja van, ezek a foglalt mezők az átlóval szomszédos két, páros sok mezőből álló átlóban vannak. Az egyik foglalt mező valamelyik páros átló végén lesz. Ez a páros átló csak a hosszabb páros átló lehet.
A tábla szélén minden mező egy páros és egy páratlan átlónak a vége. A páros átlóval szomszédos, alatta lévő páratlan átló miatt ennek a páros átlónak az egyik vége foglalt. Ezért a táblázat szélső mezőinek a fele foglalt. A két 12 mezőből álló átlónak is foglalt az egyik vége, azaz a négy sarokmezőből kettő foglalt.
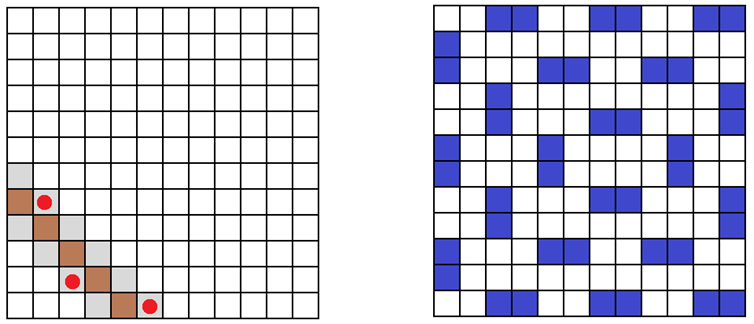
Illesszünk a tábla széléhez, a foglalt mezők mellé egy-egy újabb mezőt. A sarokban lévő foglalt mezőnek két szabad oldala van a tábla szélén, amikhez egy-egy új mezőt illesztünk. Az új táblán minden foglalt mezőhöz tartozik három vele szomszédos üres mező. Így a táblát feldarabolhatjuk 4-4 mezőből álló részekre, melyekben az egyik mező foglalt.
A tábla szélén 44 mező van, ennek a fele, 22 mező foglalt.  mezőt illesztettünk a tábla széléhez, ezért a bővített tábla
mezőt illesztettünk a tábla széléhez, ezért a bővített tábla  mezőből áll. Ha sikerült az útmutatás szerint a táblázatra bábukat helyezni, akkor ennek a 168 mezőnek a negyede, 42 mező lesz foglalt.
mezőből áll. Ha sikerült az útmutatás szerint a táblázatra bábukat helyezni, akkor ennek a 168 mezőnek a negyede, 42 mező lesz foglalt.
42 mező lesz foglalt, sem több, sem kevesebb.
D&2d azokból az esetekből indult el, hogy hogyan lehet egy sarokmezőnek egy szomszédja. A három esetből egy ellentmondásra vezetett, kettő pedig ugyanahhoz az elrendezéshez, amit fentebb is láthatunk.
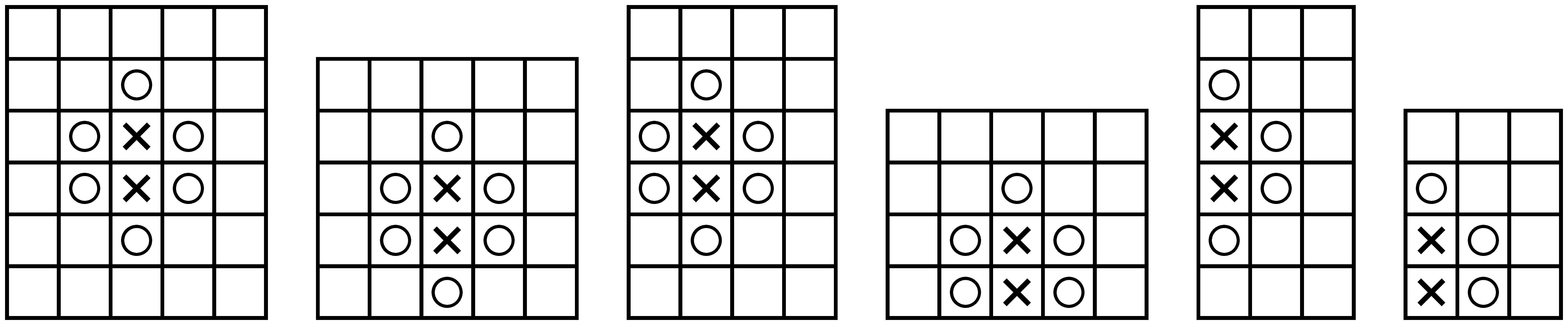
Makay Géza megoldása vázlatosan: A foglalt mezők párokban vannak. Ezek és a velük szomszédos üres mezők 6-féle típusba sorolhatók:
A konfigurációk száma legyen 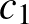 ,
, 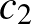 ,
, 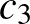 ,
, 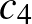 ,
, 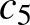 ,
, 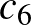 . A konfigurációk átfedés nélkül lefedik a tábla szélét, és lefedik a tábla belsejét, így a
. A konfigurációk átfedés nélkül lefedik a tábla szélét, és lefedik a tábla belsejét, így a 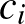 -kre felírhatunk két egyenletet. További feltételek is felírhatók, hiszen a második és harmadik elhelyezés esetén a tábla szélén kimaradó szomszédos mezőket csak az ötödik és hatodik elhelyezési móddal tudjuk lefedni mindkét oldalon, és legalább az egyik oldalon csak az ötödik elhelyezési móddal. A hatodik elhelyezési módból persze maximum 4 lehet, hiszen azt csak a sarkokba lehet elhelyezni. Mennyit fednek le a konfigurációk a tábla belsejében lévő
-kre felírhatunk két egyenletet. További feltételek is felírhatók, hiszen a második és harmadik elhelyezés esetén a tábla szélén kimaradó szomszédos mezőket csak az ötödik és hatodik elhelyezési móddal tudjuk lefedni mindkét oldalon, és legalább az egyik oldalon csak az ötödik elhelyezési móddal. A hatodik elhelyezési módból persze maximum 4 lehet, hiszen azt csak a sarkokba lehet elhelyezni. Mennyit fednek le a konfigurációk a tábla belsejében lévő 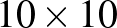 -es tábla széléből? Ez ad még egy újabb, hatodik feltételt a
-es tábla széléből? Ez ad még egy újabb, hatodik feltételt a 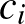 számokra.
számokra.
Egy kis programot írva erre ezeknek a feltételeknek csak olyan 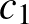 ,
, 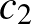 ,
, 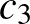 ,
, 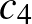 ,
, 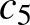 és
és 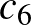 számok felelnek meg, amelyek összege 21, vagyis 42 bábu kell legyen a táblán. („Tudhattam volna, hiszen ez a válasz az életre, a világmindenségre, meg mindenre is.” [Galaxis útikalauz stopposoknak] ☺)
számok felelnek meg, amelyek összege 21, vagyis 42 bábu kell legyen a táblán. („Tudhattam volna, hiszen ez a válasz az életre, a világmindenségre, meg mindenre is.” [Galaxis útikalauz stopposoknak] ☺)
Dombi Péter és Udvari Tibor belátja, hogy páratlan oldalhosszúságú táblán nem létezik ilyen elrendezés.
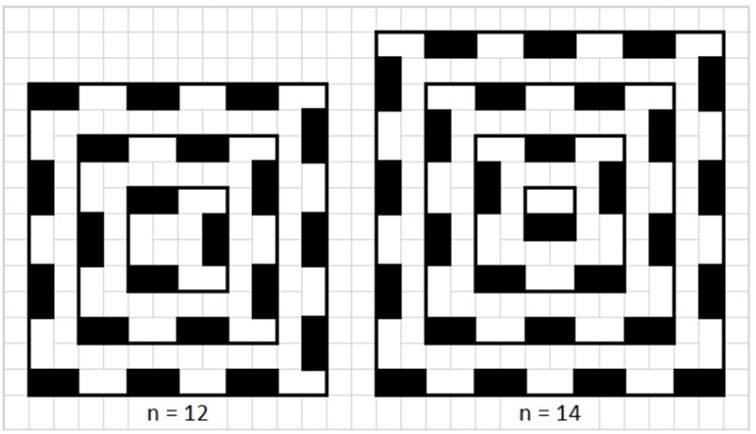
Páros oldalhosszúságú táblán minden elrendezés elfordítással vagy tükrözéssel az ábrán látható helyzetbe hozható, azaz nemcsak az elemszám, hanem maga a konfiguráció is egyértelműen meghatározott. Ekkor az 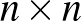 -es táblára
-es táblára 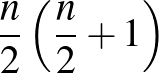 bábu helyezhető.
bábu helyezhető.
46. Hányféleképp tölthető ki egy 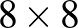 -as táblázat az 1 és
-as táblázat az 1 és 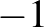 számokkal úgy, hogy a táblázat bármelyik
számokkal úgy, hogy a táblázat bármelyik 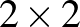 -es részében az ott álló négy szám összege nulla legyen?
-es részében az ott álló négy szám összege nulla legyen?
A válasz: 510.
Megoldás: Nézzük az első oszlop kitöltését. Két eset lehet, ha a szomszédos számok különböznek, illetve ha van két szomszédos 1, vagy 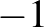 .
.
Ha az első oszlopban az 1 és 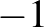 számok váltakozva követik egymást – két ilyen sorrend van –, akkor a második oszlop kitöltése is kétféle lehet, ott is váltakozva jön ez a két szám (vagy megismétlődik az első oszlop, vagy az első oszlop „tükörképét” írjuk). A további oszlopok feltöltése is kétféleképpen lehetséges. Ez összesen
számok váltakozva követik egymást – két ilyen sorrend van –, akkor a második oszlop kitöltése is kétféle lehet, ott is váltakozva jön ez a két szám (vagy megismétlődik az első oszlop, vagy az első oszlop „tükörképét” írjuk). A további oszlopok feltöltése is kétféleképpen lehetséges. Ez összesen 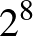 különböző táblázat.
különböző táblázat.
Másik lehetőség az, hogy az első oszlopban van két szomszédos 1-es, vagy van két szomszédos 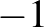 . Mondjuk van két 1-es. Mellettük két szomszédos
. Mondjuk van két 1-es. Mellettük két szomszédos 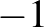 van a második oszlopban, és ennek a két sornak a további feltöltése egyértelmű. Az első oszlop számai és ez a két sor egyértelműen meghatározza többi számot is a táblázatban.
van a második oszlopban, és ennek a két sornak a további feltöltése egyértelmű. Az első oszlop számai és ez a két sor egyértelműen meghatározza többi számot is a táblázatban.
Azt látjuk, ha az első oszlopban van két szomszédos 1 vagy 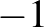 , akkor ennek a táblázatnak egyféle kitöltése van. A lehetséges első oszlopok száma
, akkor ennek a táblázatnak egyféle kitöltése van. A lehetséges első oszlopok száma 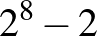 .
.
A jó kitöltésű táblázatok száma 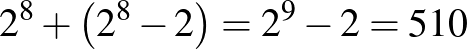 .
.
Megjegyzések. A helyzetet így jellemzi Berkó Erzsébet: Ahogyan az életben meghatározó az első néhány év, ehhez hasonlóan itt meghatározó az első sor (vagy az első oszlop).
Makay Géza átfogalmazta a feladatot: hányféleképpen színezhető fekete-fehérre a sakktábla úgy, hogy minden 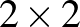 -es részében ugyanannyi fekete és fehér mező legyen?
-es részében ugyanannyi fekete és fehér mező legyen?
Bizonyítja általános esetre, hogy az 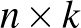 -as tábla színezéseinek száma
-as tábla színezéseinek száma 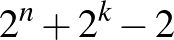 .
.
47. Egy 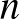 -oldalú konvex sokszöget szétvágtunk három konvex sokszögre. Az egyiknek
-oldalú konvex sokszöget szétvágtunk három konvex sokszögre. Az egyiknek 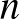 oldala van, a másiknak
oldala van, a másiknak 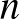 -nél több, a harmadiknak pedig
-nél több, a harmadiknak pedig 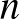 -nél kevesebb. Mennyi lehet
-nél kevesebb. Mennyi lehet 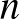 legnagyobb értéke?
legnagyobb értéke?
A válasz: 5.
Megoldás: A darabolás után kapott sokszögek oldalainak száma rendre 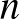 , legalább
, legalább 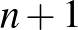 , és legalább 3. Nyilván
, és legalább 3. Nyilván 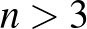 . A három sokszög oldalait összeadva az eredmény legalább
. A három sokszög oldalait összeadva az eredmény legalább 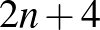 .
.
Belátjuk, hogy ha 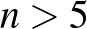 , akkor nincs alkalmas sokszög, amelyet az elvárások szerint feldarabolhatunk.
, akkor nincs alkalmas sokszög, amelyet az elvárások szerint feldarabolhatunk.
A sokszög feldarabolása után a kapott három sokszög oldalaiból a feldarabolt sokszög belsejében lehet 2 vagy 3. Előbbi esetén a sokszög oldalain legfeljebb 4, utóbbi esetén pedig legfeljebb 3 oldalpár alkotja a feldarabolt sokszög egy-egy oldalát.
Az első lehetőségnél a belül lévő oldalak miatt  -et, a kintiek miatt legfeljebb 4-et hagyunk el, és megkapjuk az eredeti sokszög oldalainak számát,
-et, a kintiek miatt legfeljebb 4-et hagyunk el, és megkapjuk az eredeti sokszög oldalainak számát,  -et. Mivel legalább
-et. Mivel legalább 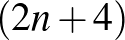 -ből legfeljebb 8-at hagyunk el, így legalább
-ből legfeljebb 8-at hagyunk el, így legalább 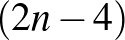 marad.
marad.
Azonban 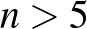 esetén
esetén 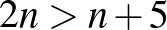 , azaz
, azaz 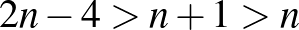 , tehát a három sokszög együtt nem alkothat
, tehát a három sokszög együtt nem alkothat 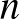 -oldalú sokszöget.
-oldalú sokszöget.
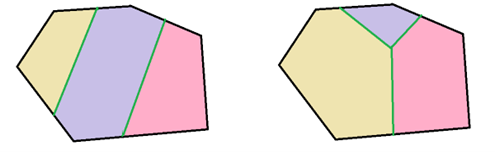
A második lehetőségnél a belül lévő oldalak miatt legfeljebb  -ot, a kintiek miatt legfeljebb 3-at hagyunk el, és megkapjuk az eredeti sokszög oldalainak számát,
-ot, a kintiek miatt legfeljebb 3-at hagyunk el, és megkapjuk az eredeti sokszög oldalainak számát, 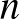 -et. Mivel legalább
-et. Mivel legalább 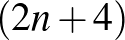 -ből legfeljebb 9-et hagyunk el, így legalább
-ből legfeljebb 9-et hagyunk el, így legalább 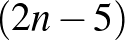 marad.
marad.
Azonban 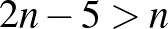 , így
, így 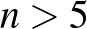 , tehát a három sokszög együtt nem alkothat
, tehát a három sokszög együtt nem alkothat  -oldalú sokszöget, ha az oldalak száma
-oldalú sokszöget, ha az oldalak száma 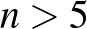 .
.
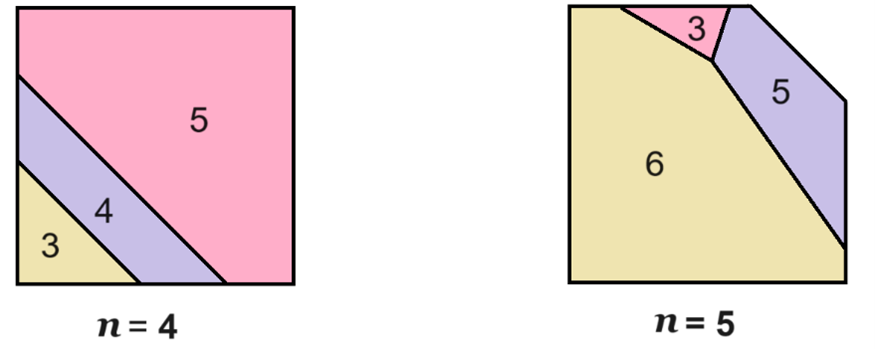
Ha 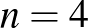 vagy 5, akkor van alkalmas darabolás.
vagy 5, akkor van alkalmas darabolás.
48. A 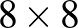 -as sakktáblára egyesével helyezünk királynőket. A következő királynő legfeljebb egy másikat tarthat ütés alatt az előzőleg elhelyezett királynők közül. Legfeljebb hány királynőt helyezhetünk így a táblára?
-as sakktáblára egyesével helyezünk királynőket. A következő királynő legfeljebb egy másikat tarthat ütés alatt az előzőleg elhelyezett királynők közül. Legfeljebb hány királynőt helyezhetünk így a táblára?
A válasz: 14.
Megoldás: Tekintsük a tábla 8 sorát, 8 oszlopát, a főátlóval párhuzamos 7 átlót a fehér mezőkkel, és a mellékátlóval párhuzamos 7 átlót a fekete mezőkkel. Az első királynő ebből a 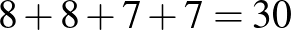 egyenesből hármat elfoglal. A szabadon maradó 27 egyenesből minden újabb vezér legalább kettőt elfoglal, így az első királynő után legfeljebb
egyenesből hármat elfoglal. A szabadon maradó 27 egyenesből minden újabb vezér legalább kettőt elfoglal, így az első királynő után legfeljebb 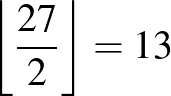 további bábut tehetünk fel. A táblán nem lehet 14-nél több királynő.
további bábut tehetünk fel. A táblán nem lehet 14-nél több királynő.

A számok mutatják, hogy milyen sorrendben helyezhetünk 14 királynőt a táblára.
Megjegyzés. A feladat igen nehéznek bizonyult, a megoldás rövidsége ne tévessze meg az Olvasót. (Ezt a mondatot kölcsönvettem a KöMaL 2006. márciusi számában megjelent Variációk egy versenyfeladatra c. cikkből.)
49. A megyei labdarúgó-bajnokságot a Csodacsapat nyerte, és a Falábúak végeztek az utolsó helyen. A bajnokságban bármely két csapat pontosan egy mérkőzést játszott egymással, a győztes 3 pontot, a vesztes 0 pontot kapott, döntetlen esetén pedig mindkét csapatnak 1-1 pont járt. A csapatokat a szerzett pontszámok alapján rangsorolták.
Legkevesebb hány csapat indult a bajnokságban, ha az a meglepő helyzet állt elő, hogy a régi pontszámítás szerint (amikor a győzelemért 3 pont helyett 2 pont jár) más lenne a végeredmény: a Falábúaké az első hely, és a Csodacsapat végez az utolsó helyen? (Mindkét pontszámítás esetén az első és az utolsó helyezett holtverseny nélkül érte el az eredményt.)
A válasz: 12.
Megoldás: Ha a Falábúaknak nincs győztes mérkőzése, akkor a lehetséges pontszámnak legfeljebb a felét szerzik meg a 2-1-0 pontozás szerinti rendszerben, de ezzel nem előzik meg a többi csapatot, nem lehetnek első. A Falábúak csapatának van legalább egy győztes meccse. Emiatt a csapat pontszáma legalább 1 ponttal csökken, ha a győztes meccsért 3 pont helyett 2 pontot kapnak.
A Csodacsapat pontszáma nagyobb a többi csapat pontszámánál, a Falábúak pontszáma kisebb mindenkinél, így egalább 2 pont köztük a különbség. A másik pontszámítás szerint felcserélődik ez a két szerep, közben a Falábúak pontszáma csökken legalább 1 ponttal, ezért a Csodacsapat pontszáma legalább 5 ponttal csökken a 2-1-0 pontszámítással.
Tehát a csapatnak van 5 győzelme, mégis az utolsó helyen végez, emiatt van 6 veresége is, így a csapat legalább 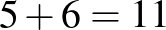 csapattal játszik. A bajnokságban legalább 12 csapat indult.
csapattal játszik. A bajnokságban legalább 12 csapat indult.
A feltételeknek megfelelő 12-csapatos bajnokság a következő. A Csodacsapat és a Falábúak mellett még 10 csapat játszik, őket jelöljük az 1, 2, ..., 10 számokkal, ők a páros és a páratlan csapatok.
A Csodacsapat legyőzte a páros csapatokat, a többiektől vereséget szenvedett. Így a bajnokság végén a kétféle számítás szerint 15, illetve 10 pontot szerez.
A Falábúaknak egy győzelme van a Csodacsapat ellen, a többiekkel döntetlent játszott. Ezzel 13, illetve 12 pontot szerez.
A páros csapatok egymás között döntetlent játszottak, és a páratlan csapatoknak is döntetlen játszmái vannak egymás között.
Írjuk egy körre egymás után az 1, 2, ..., 10 számokat. A páratlan csapatok legyőzték a két szomszédos páros csapatot, és kikaptak a többi három páros csapattól.
A páros csapatoknak 3 győzelme van a páratlanok ellen, és 3 veresége is, a Csodacsapattól és két páratlantól. A többi mérkőzése döntetlen. A páratlan csapatoknak ugyancsak 3 győzelme, 3 veresége és 5 döntetlen mérkőzése van. Mind a tíz csapatnak 14, illetve 11 pontja van.
A 3-1-0 pontszámítás alapján a Csodacsapat 15 ponttal az első, a Falábúak 13 ponttal szerepelnek a tabella végén, mivel a többieknek 14 pontja van. Ugyanez a 2-1-0 pontozással a Falábúakat hozza első helyre 12 ponttal, nyomában van a tíz számozott csapat 11 ponttal, és a Csodacsapat 10 ponttal az utolsó.
D&2d válasza: 12 csapat indult a bajnokságban.
Falábúak 1 győzelem, 10 döntetlen.
Csodacsapat 5 győzelem, 6 vereség.
Többi csapat egyenként: 3 győzelem, 5 döntetlen, 3 vereség.
Az új pontszámítás szerint Csodacsapat: 15 pont, többi csapat egyenként 14 pont, Falábúak 13 pont.
A régi pontszámítás szerint: Falábúak 12 pont, többi csapat egyenként 11 pont, Csodacsapat 10 pont.
a Héttusa rovat vezetője











