Egy igazán sokoldalú matematikai jelenséget szeretnék bemutatni: a Hopf-fibrálást. A tárgyalásmód szándékom szerint ismeretterjesztő, matematikai előképzettséget nem igényel. Ez nem azt jelenti, hogy mindenki ugyanúgy meg fogja érteni, hiszen ezt egy vers, egy színdarab vagy egy film esetén sem várjuk el. Hanem azt jelenti, hogy mindenki számára hordozhat személyes jelentést, mindenkinek mást és mást. Nekem is személyes okaim vannak arra, hogy mindezt leírjam. A Hopf-fibrálás a topológiai jelentősége miatt lett a kedvenc képletem, de ez az aspektusa nehezen átadható. A zenekarom Dinamikus Meditáció c. lemezének borítójához gézből készítettük el a Hopf-köröket a dalszövegekben többször említett titokzatos eredetű szétfutó és becsavaró szálak szimbólumaként. Tavaly ősz óta pedig fizikus kollégáimmal próbáljuk megérteni bizonyos kvantumrendszerek matematikai leírását, ennek során vettük észre a Hopf-fibrálás és a qubit szoros kapcsolatát. Nem újkeletű a gondolat, ennek ellenére sem ők, sem mi matematikusok nem szoktunk így gondolni rá. Idén januárban a Kéregfeszten tartottam egy MateMorfózis ismeretterjesztő előadást erről a témáról, ahhoz írtam ezt az összefoglaló cikket. „Gergő, te úgy gondolod, hogy a qubit megértésének leghatékonyabb módja a Hopf-fibrálás?” – kérdezték a fizikusok. Nem. De a kettő ugyanaz, állapítottuk meg. Tehát ez egy matematikailag is teljesen korrekt, teljes kép, és ehhez képest könnyen befogadható.

A Dinamikus Meditáció lemezborítója
Hogyan alakulnak át egymásba a címben említett, első hallásra nagyon különbözőnek tűnő minőségek? A Hopf-fibrálás egy vetítésekhez, vizuálokhoz gyakran felhasznált csavarodó, örvényszerű mintázat. Ez a mintázat teljes pompájában egymást áthurkoló körökből áll, amelyek összességében (kis híján) kitöltik a teret. Ez az elrendezés valójában egy négydimenziós mintázat vetülete a háromdimenziós térbe. A négydimenziós mintázat sokkal természetesebb és szimmetrikusabb, mint az e világi „árnyéka”, csak nem tudjuk közvetlenül ábrázolni. De több oldalról megközelítve egészen kielégítő képet kaphatunk róla. A négydimenziós kép a qubit matematikai modellje. A hagyományos számítógépekben az információ alapegysége a bit, egy két állapotú jel. A bit kvantuminformációs megfelelője egy kétállapotú kvantumrendszer, mint például az elektron spinje vagy Schrödinger macskájának gondolatkísérlete. Egy kvantumbit állapota is 0 vagy 1 lehet, de hogy melyik, az csak a konkrét mérés során derül ki, egyébként a kettő között lebeg valamekkora valószínűséggel. A qubit azonban jóval komplexebb, mint az igen-nem válasz valószínűsége, a teljes állapota a Hopf-fibrálásban van elkódolva. A Hopf-fibrálás egy topológiai jelenség, a Möbius-szalag és a Klein-kancsó közeli rokona, egy magasabb dimenziós csavarodó nyaláb.
Ezen az úton fogunk hát végighaladni, a látványos vizuálokból kiindulva felgöngyölítjük a szálakat a Möbius-szalagtól négydimenziós kitérővel a qubitig.
1. Mik ezek a spirálszerűen csavargó vonalak?

A Hopf-körök (beleértve a középsőt, ami nem kör, hanem egyenes) kitöltik a teret, miközben bármelyik kettő áthurkolódik egymáson, mint két láncszem, ún. Hopf-linket alkotva.
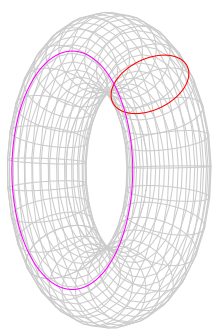
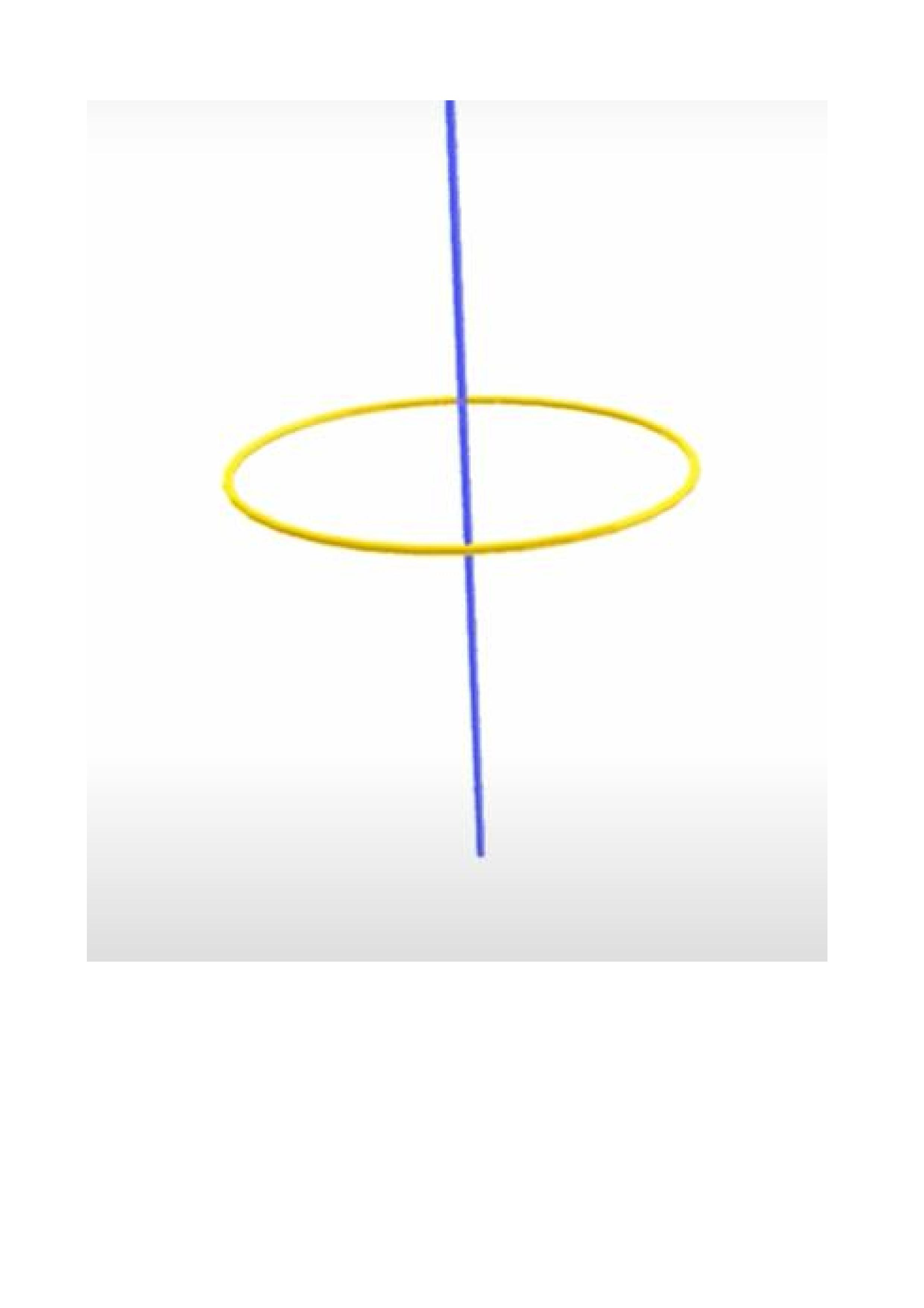
A következőképpen kaphatjuk meg ezt a mintázatot. Induljunk ki a térben egy körből, és a kör síkját a kör középpontjában merőlegesen átdöfő egyenesből – mint egy képzeletbeli búgócsiga határvonala és forgástengelye, az ábrán a kékek között megbúvó piros kör és egyenes. Ha a kört lassan megvastagítjuk a térben, körbezáródó csöveket, ún. tóruszokat kapunk körülötte. Ezek az egyre dagadtabb úszógumi-felületek összességében kitöltik a teret, a kiindulási kör és egyenes kivételével. Amikor már az úszógumi külső fala a végtelenbe dagadva bekebelezi az egész teret, a belső lyuk rászűkül az egyenesre. Így ezek az egyre növekvő, egymást tartalmazó tóruszok a kiindulási körből erednek és az egyenesben végződnek.
A teret a kiindulási körrel és egyenessel együtt kitöltő tóruszok egy úgynevezett elliptikus vagy másnéven appolóniuszi körsor megforgatásából származnak.
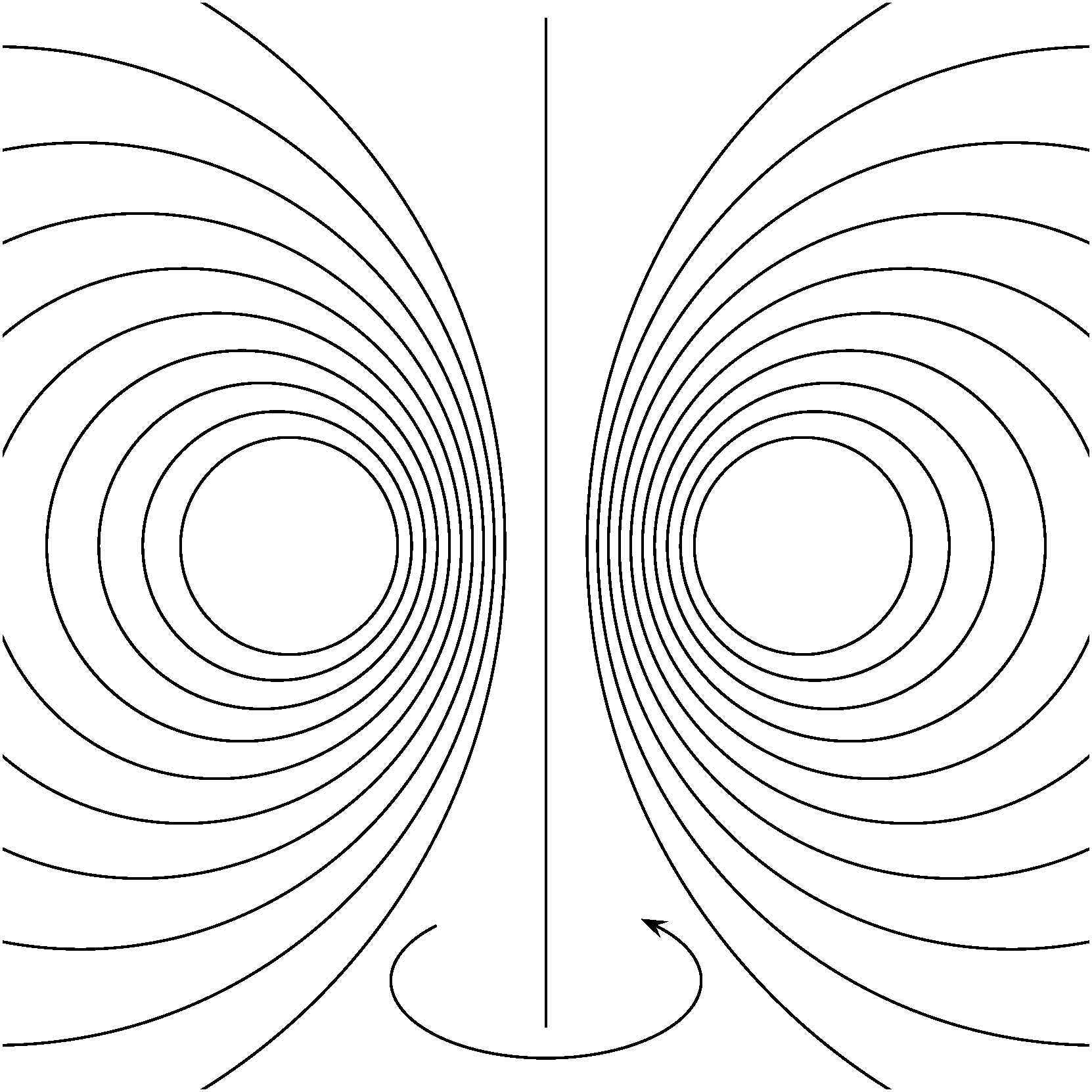
Ezután a teret kitöltő tóruszok felületeire rajzoljuk rá a „ferdén futó” köröket! Egy tóruszon két jellemző irányban tudunk körbemenni, az ún. meridián vagy a longitúdó mentén. (Ezt mutatom a videón is.)
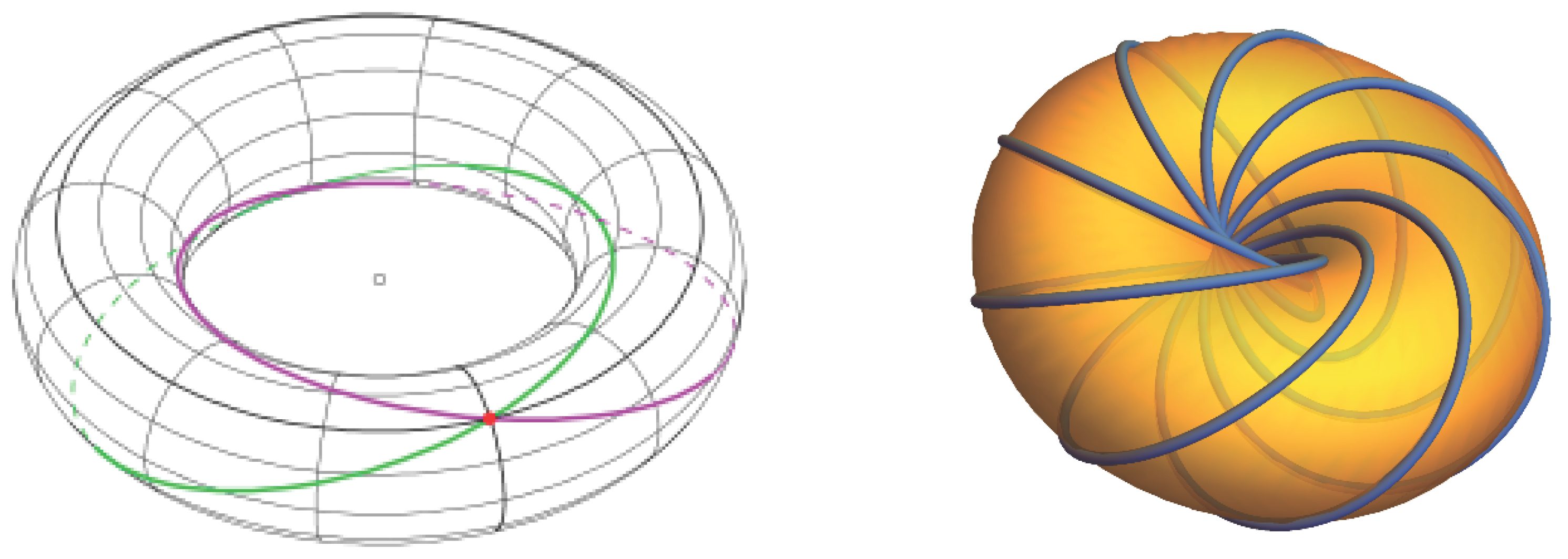

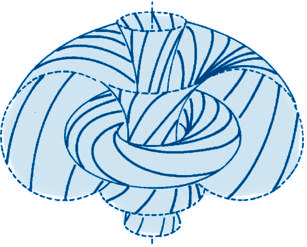
A ferdén futó körök a meridián és a longitúdó irányában is egyszer mennek körbe a felületen, ahogyan azt az ábra mutatja. Minden tórusz felületén két seregnyi van ilyen körökből, ezek közül az egyik irányút ki kell választanunk egyszer és mindenkorra az összes tóruszon. A kiindulási körre rázsugorodó tóruszok ferdén menő körei végül rásimulnak a kiindulási körre, míg az egyre dagadó tóruszok körei a kijelölt tengelyhez egyenesednek. Így a kiindulási kört és egyenest is beleszámítva a Hopf-körök kitöltik a teret. Semelyik kettő nem metszi egymást, azaz nem érnek össze, nincsen közös pontjuk, de szétválaszthatatlanok, mert egymásba láncolódnak.

Terjed mostanában egy játék, ami emlékeztet erre a mintázatra, ez a toroflux. Azonban a toroflux nem Hopf-körökből áll, hanem ő maga egyetlen kör, ami 13-szor, illetve 14-szer kerüli meg a tóruszt a meridián, illetve a longitúdó irányában. A toroflux egy ún. tóruszcsomó.

Az itt vázolt attraktív csavaros kép a Hopf-fibrálás háromdimenziós képe. De pusztán az érzékien összetett szépség még nem lenne elég ok arra, hogy a kedvenc képletemként emlegessem. A Hopf-fibrálás valójában a négydimenziós térben él teljes pompájában. A Hopf-körök a négydimenziós térbeli gömbfelületet töltik ki teljesen szimmetrikus módon. A négydimenziós térbeli körök mind azonos méretűek, és tényleg mind körök, nincsen köztük egyenes. Az eredetileg egyforma körök képei ugyanúgy nyúlnak meg a háromdimenziós térben, mint az árnyékunk naplemente előtt. A képeken valójában a Hopf-fibrálás háromdimenziós árnyékát látjuk. Erről bővebben a következő utáni fejezetben lesz szó.
Magát a fibrálást képlettel így fejezhetjük ki:
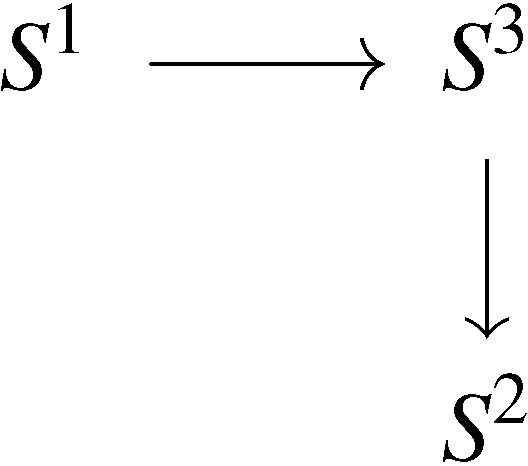
A képlet azt mondja, hogy a (négydimenziós térbeli) háromdimenziós gömbfelület kétdimenziós gömbfelületnyi sok egydimenziós gömbfelületre, azaz körvonalra bontható. Az ilyen „rostokra bontásról” szól a most következő fejezet.
2. Fibrált nyalábok
A matematika topológia, illetve algebrai geometria nevű ágaiban a 20. század első felében kicsit elburjánoztak a mezőgazdasági elnevezések, a nyalábok és a kévék az absztrakt matematika – és mint látni fogjuk, valahol mélyen a fizika – kulcsfontosságú struktúrái. A nyalábok egymáshoz simuló fibrumokra (azaz rostokra) bontott, vagy ha úgy tetszik, fibrumokból felépített terek. A hengerpalást például alkotókra bontható, körvonalnyi sok szakasz alkotja. Vagy fordítva: szakasznyi sok körvonal. Ez két különböző nyalábnak felel meg, az első esetben a szakaszok (intervallumok) a fibrumok, és a bázistér a körvonal, aminek minden pontjához tartozik egy alkotó szakasz. A második esetben a körvonalak a fibrumok, és a szakasz a bázis. Mindkét nyaláb esetén az ún. totális tér maga a hengerpalást. Egy nyaláb esetén tehát fibrumokból építünk fel egy totális teret a bázistér szerint.

A henger két különböző nézőpontból is nyaláb: körvonalnyi sok szakasz és szakasznyi sok körvonal egyúttal. A hengerpaláston mászkálva a pozíciónkat egyértelműen azonosíthatjuk, ha megmondjuk, hol járunk a körön, illetve a szakaszon. Azaz: a henger egy körvonal és egy szakasz ún. Descartes-szorzata.
Hasonlóképp áll elő a tóruszfelület mint körvonalnyi sok körvonal, kétféleképpen is. A tórusz tehát két körvonal Descartes-szorzata. A legismertebb Descartes-szorzat a Descartes-féle koordinátarendszer, miszerint a sík két egyenes, a két tengely Descartes-szorzata. Egy pont két koordinátája megadja, hogy hol járunk az ![]() , illetve az
, illetve az ![]() tengely mentén.
tengely mentén.
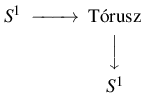
 Nézzük meg ellenpéldának a bolygónk felszínét, ami egy térbeli gömbfelület! A gömbfelület jele
Nézzük meg ellenpéldának a bolygónk felszínét, ami egy térbeli gömbfelület! A gömbfelület jele ![]() : „S” mint sphere, és 2, minthogy kétdimenziós. Igen, kétdimenziós, mert a felületi közlekedésünket 2 GPS-koordinátával tudjuk lekövetni. Harmadik koordináta, a magasság csak akkor kell, ha repülünk vagy a Föld mélyére ásunk, de akkor már nem a gömbfelületen vagyunk. A GPS-koordináták alapján azt gondolhatnánk, hogy a gömbfelület is Descartes-szorzat, de ez nem így van. A GPS-koordináták ugyanis elromlanak az északi és a déli sarkon, nem egyértelműen koordinátázzák a gömbfelületet. A gömbfelület nem is nyaláb, ha szakasz vagy kör fibrummal próbálkozunk, a hosszúsági körök például találkoznak a sarkokban, a szélességi körök pedig nem találkoznak egymással, de a sarkokban pontokká zsugorodnak.
: „S” mint sphere, és 2, minthogy kétdimenziós. Igen, kétdimenziós, mert a felületi közlekedésünket 2 GPS-koordinátával tudjuk lekövetni. Harmadik koordináta, a magasság csak akkor kell, ha repülünk vagy a Föld mélyére ásunk, de akkor már nem a gömbfelületen vagyunk. A GPS-koordináták alapján azt gondolhatnánk, hogy a gömbfelület is Descartes-szorzat, de ez nem így van. A GPS-koordináták ugyanis elromlanak az északi és a déli sarkon, nem egyértelműen koordinátázzák a gömbfelületet. A gömbfelület nem is nyaláb, ha szakasz vagy kör fibrummal próbálkozunk, a hosszúsági körök például találkoznak a sarkokban, a szélességi körök pedig nem találkoznak egymással, de a sarkokban pontokká zsugorodnak.
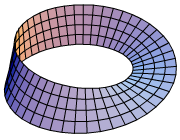
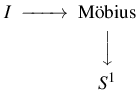
De ha csak szorzatként előálló alakzatokat (tereket) vizsgálnánk, azért fölösleges volna nyalábokról beszélnünk. A nyalábok lényegéhez tartozik a csavarodás, amit a hengeren és a tóruszon pont nem látunk, de a Hopf-fibráláson annál szembetűnőbb. Vegyünk egy hosszúkás téglalap alakú papírt, és ragasszuk össze a két szélét, de ragasztás előtt az egyik szélét csavarjuk meg egy fél fordulattal! Így kapjuk a Möbius-szalagot. A Möbius-szalag is körvonalnyi sok szakasz, akárcsak a henger, de szakasznyi sok körvonalként már nem áll elő, éppen a csavarodás miatt. Ennek megvizsgálását az olvasóra bízom, mivel jóval érdekesebb jelenségekről van szó, minthogy csak úgy lelőjem a poént: próbálja csak meg berajzolni a köröket a Möbiuson, esetleg szétvágni a szalagot a középkör mentén!
Feladat a kiváncsi olvasónak:
– Készíts papírból egy Möbius-szalagot! Ragaszd jól össze a téglalap széleit!
– Rajzold be a Möbius-szalag középkörét! Valami meglepő már ekkor is fog történni...
– Indíts el körben egy másik vonalat a középkör mentén, de attól kijjebb, a széle felé. Hogyan tudnád bezárni, miután egyszer(!) körbeértél?
– Ha meguntad, vágd szét a Möbius-szalagot a középkör mentén! Tippeld meg előtte, mi fog történni!

Ahogy a henger csavarodott változata a Möbius-szalag, a tórusznak is van csavarodott testvére. Ez a Klein-kancsó, ami egy cső önmagán keresztül átdugva, majd a két peremköre mentén összeragasztva. Egyféleképpen körvonalnyi sok körvonal, de a Möbius-szalaghoz hasonlóan nem lehet felbontani egymás mellé simuló másik irányú körökre. Ezekről az alakzatokról részletesebben és más megvilágításban szól a Térteremtés c. előadásom.

 Ez a két kép egy youtube animációból való, ami azt mutatja, hogy a Hopf-fibrálás esetén a gömbfelület minden pontjához tartozik egy Hopf-kör. A déli sark az eredetileg kijelölt (vízszintes) kört jelképezi, az északi sark az egyenest. A szélességi körökhöz egy-egy tórusz ferdén álló körei tartoznak. (Ez persze mind a választásunk kérdése: a gömb pólusait, az alapkört és a függőleges egyenest úgy választjuk meg, ahogy akarjuk.) Az egyetlen ami nem stimmel, hogy egy egyenes keveredett a körök közé. De a négydimenziós térben ez is körré záródik, csak az alkonyat az árnyékát egyenessé nyújtja.
Ez a két kép egy youtube animációból való, ami azt mutatja, hogy a Hopf-fibrálás esetén a gömbfelület minden pontjához tartozik egy Hopf-kör. A déli sark az eredetileg kijelölt (vízszintes) kört jelképezi, az északi sark az egyenest. A szélességi körökhöz egy-egy tórusz ferdén álló körei tartoznak. (Ez persze mind a választásunk kérdése: a gömb pólusait, az alapkört és a függőleges egyenest úgy választjuk meg, ahogy akarjuk.) Az egyetlen ami nem stimmel, hogy egy egyenes keveredett a körök közé. De a négydimenziós térben ez is körré záródik, csak az alkonyat az árnyékát egyenessé nyújtja.
Evvel a cikkel egy időben jelent meg a https://indiecrawford.blog.hu/
3. A négydimenziós térbeli gömb és a háromdimenziós árnyékvilág
Gömbök minden dimenzióban vannak. A síkon a körvonal olyan pontokból áll, amelyek egy adott középponttól egyenlő távol helyezkednek el. A körvonal az egydimenziós gömbfelület, ![]() , természetes élőhelye a két dimenziós sík. A térben ugyanezzel a meghatározással gömbfelületet kapunk, az
, természetes élőhelye a két dimenziós sík. A térben ugyanezzel a meghatározással gömbfelületet kapunk, az ![]() kétdimenziós gömbfelületet. Ugyanígy egy négydimenziós térben adott ponttól egyenlő távolságra fekvő pontok egy háromdimenziós önmagába forduló alakzatot alkotnak, ez a háromdimenziós gömbfelület,
kétdimenziós gömbfelületet. Ugyanígy egy négydimenziós térben adott ponttól egyenlő távolságra fekvő pontok egy háromdimenziós önmagába forduló alakzatot alkotnak, ez a háromdimenziós gömbfelület, ![]() . A háromdimenziós gömbfelület nem tévesztendő össze az általunk ismert gömb belsejével, a golyóval. A golyó egy kétdimenziós gömbfelülettel körbezárt világ: ha egy gumilabda belsejeként gondolunk rá, nem tudunk belőle kilépni, falba ütközünk. A háromdimenziós gömbfelületet nem határolják falak, az egy olyan tér, amelyben akármilyen irányban utazva előbb-utóbb körbeérünk.
. A háromdimenziós gömbfelület nem tévesztendő össze az általunk ismert gömb belsejével, a golyóval. A golyó egy kétdimenziós gömbfelülettel körbezárt világ: ha egy gumilabda belsejeként gondolunk rá, nem tudunk belőle kilépni, falba ütközünk. A háromdimenziós gömbfelületet nem határolják falak, az egy olyan tér, amelyben akármilyen irányban utazva előbb-utóbb körbeérünk.
Felmerül a kérdés, hogy a mi az a négydimenziós tér. Ez szerintem egy nagyon fontos kérdés, és a hétköznapi életünkben, világszemléletünkben és önmeghatározásunkban is fontos szerepe lehet, ugyanis nem vagyunk bezárva a 3 dimenzióba – főképp nem a gondolkodásunk! A matematikai térfogalom egy teljesen szabad felhasználású modellező eszköz, egy metafóra. A fizikai tér, az idő, a színek vagy akár a zene mind csak példák erre. Bármilyen rendszer vagy jelenség, amit 4 adattal tudunk jellemezni, modellezhető egy négydimenziós térben. A magasabb dimenziók a hamarosan megjelenő Új világok teremtése című könyvemben szerepelnek részletesebben. A Hopf-fibrálás viszont alkalmas arra, hogy segítségével képet kapjunk a négydimenziós tér és az ottani gömb szerkezetéről.
Nézzük meg képeken és animációkon keresztül egy kisebb dimenziós példán, hogyan keletkezik a gömb árnyéka az ún. sztereografikus projekció által!
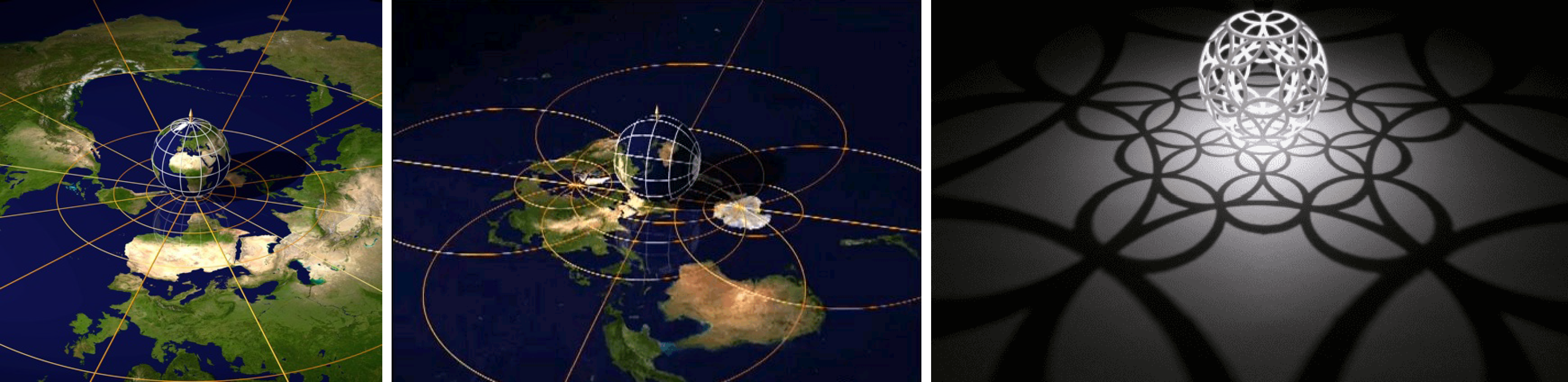
A gömbfelületet egy pontjából (nevezzük ezt északi sarknak) vetítjük az átellenes ponthoz illesztett érintősíkra. Képzeljük a gömböt egy mintás lámpabúrának az északi sarkpontban elhelyezett pontszerű fényforrással! A gömb árnyéka beteríti az egész síkot, és a mintázat eltorzul, az északi sarkhoz közeli minták árnyéka hatalmasra nő. Sőt, ha egy vonal áthalad magán a vetítési ponton, az árnyéka a síkon végtelenné nyúlik. Például az északi és déli sarkon áthaladó hosszúsági kör képe a síkon egyenes lesz. Magát a vetítési pontot a síkon nem látjuk, annak nincs árnyéka, a síkon a végtelennek felel meg. Az egész jelenséget fordítva is szemlélhetjük: a síkot egyetlen végtelen távoli pont gömbbé zárja, mint a boltívet a tetején az ékkő. Ugyanez működik a körvonal és egyenes viszonylatában is: a kört kivetíthetjük egy pontból az egyenesre, vagy fordítva, a kör az egyenes összezárása egyetlen végtelenben.
És ugyanez működik a négydimenziós térben is: az ottani gömböt, az ![]() háromdimenziós gömbfelületet egy háromdimenziós térre vetíthetjük. Ennek eredményét látjuk a térbeli Hopf-fibrálás formájában, a négydimenziós térbeli gömbi Hopf-körök elnyúlt árnyékait. Próbáljunk meg ebből a mintából visszakövetkeztetni az árnyékolóra! Az egyre nagyobb méretű körök valójában nem nagyobbak, csak közelebb vannak a fényforráshoz, a háromdimenziós gömbön kijelölt északi sarkhoz. A kiinduláskor választott egyenesünk a gömbön ugyanolyan kör, mint a többi, csak átmegy az északi sarkon, ezért nyúlik az árnyéka végtelenné. Sőt! A térben egy konkrét tóruszfelület belseje egy úgynevezett tömör tórusz, azaz egy tóruszfelülettel körbezárt véges világ, kiút nélküli körbefutó alagút. A tóruszon kívüli térrész egészen másképpen néz ki, az egy végtelen tér, csak hiányzik belőle egy tórusz alakú darab. De a háromdimenziós gömbfelületben ez a külvilág is tömör tórusz, egy zárt cső! Csak az árnyéka nyúlik végtelenné a vetítés miatt. Miképpen a kiindulási körünk a tórusz belsejében halad, a külvilággá kivetülő tömör tórusz közepén fut az a kör, aminek az árnyéka a térben a kiindulási egyenes. A két tömör tórusz a közös tóruszfelületük mentén összeragasztva, mint két egymás köré dagadt, egymást teljesen körülölelő láncszem kitöltik a három dimenziós gömbfelületet. Ez a tökéletes ölelés.
háromdimenziós gömbfelületet egy háromdimenziós térre vetíthetjük. Ennek eredményét látjuk a térbeli Hopf-fibrálás formájában, a négydimenziós térbeli gömbi Hopf-körök elnyúlt árnyékait. Próbáljunk meg ebből a mintából visszakövetkeztetni az árnyékolóra! Az egyre nagyobb méretű körök valójában nem nagyobbak, csak közelebb vannak a fényforráshoz, a háromdimenziós gömbön kijelölt északi sarkhoz. A kiinduláskor választott egyenesünk a gömbön ugyanolyan kör, mint a többi, csak átmegy az északi sarkon, ezért nyúlik az árnyéka végtelenné. Sőt! A térben egy konkrét tóruszfelület belseje egy úgynevezett tömör tórusz, azaz egy tóruszfelülettel körbezárt véges világ, kiút nélküli körbefutó alagút. A tóruszon kívüli térrész egészen másképpen néz ki, az egy végtelen tér, csak hiányzik belőle egy tórusz alakú darab. De a háromdimenziós gömbfelületben ez a külvilág is tömör tórusz, egy zárt cső! Csak az árnyéka nyúlik végtelenné a vetítés miatt. Miképpen a kiindulási körünk a tórusz belsejében halad, a külvilággá kivetülő tömör tórusz közepén fut az a kör, aminek az árnyéka a térben a kiindulási egyenes. A két tömör tórusz a közös tóruszfelületük mentén összeragasztva, mint két egymás köré dagadt, egymást teljesen körülölelő láncszem kitöltik a három dimenziós gömbfelületet. Ez a tökéletes ölelés.
A tömör tórusz végtelenné nyúlását két lépésben érthetjük meg, mivel magát a négydimenziós jelenséget ábrázolni nem tudjuk.
1. Az animáción láthatjuk a jelenség eggyel kisebb dimenziós változatát, amin egy négyzet fordul át a külvilágba.
2. A következő animáción (készítette: Márkus Benjámin) a tóruszfelület fordul ki a végtelenen keresztül. A kisebb dimenziós változathoz hasonlóan Itt is annyi történik, hogy a négydimenziós térbeli gömbfelület forog, és amikor éppen átfordul a tórusz a vetítési ponton, akkor nyúlik az árnyéka végtelenné. Csakhogy itt magát a forgó gömböt nem látjuk, csak a térbeli árnyékát.
 |
 |
 |
 |
4. Körök a gömbben
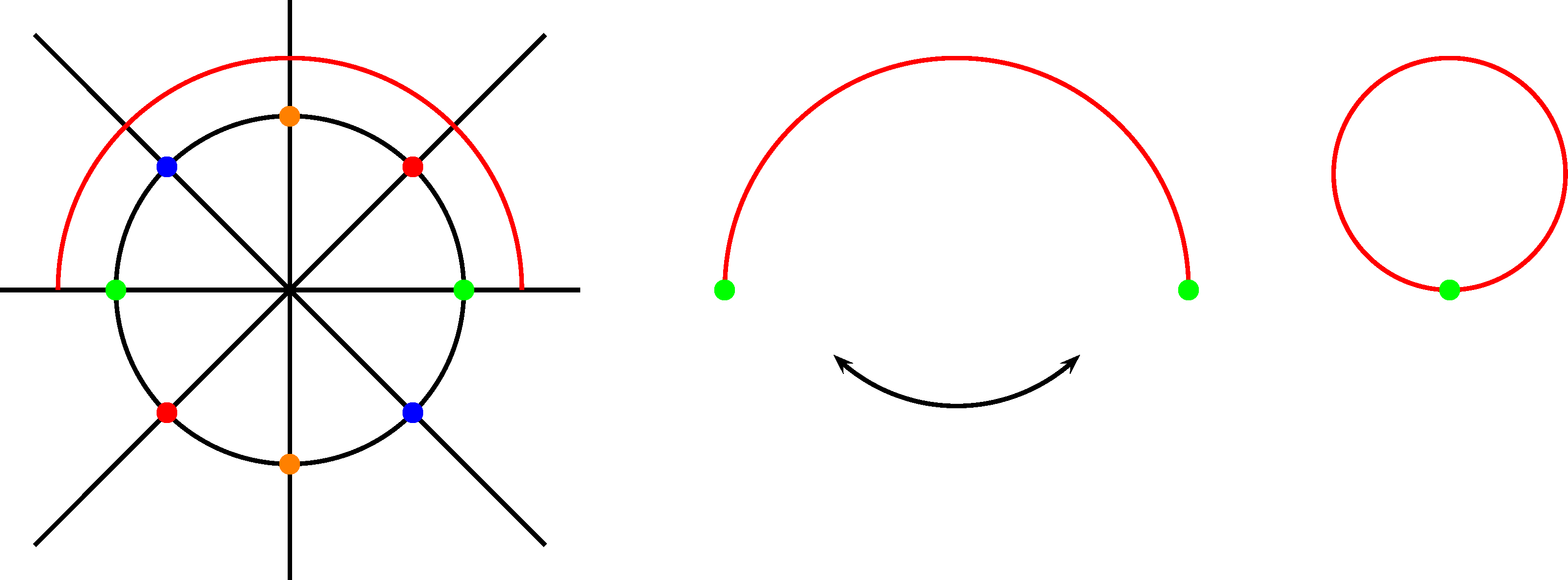
A magas dimenziók után nézzük meg most a Hopf-fibrálás „bébi verzióját”. Vegyünk a síkon egy kört és a középpontján átmenő egyeneseket! Mindegyik egyenesnek két közös pontja van a körvonallal, két átellenes pont a körön. Talán kicsinyesen hangzik, de ez is egy fibrálás: minden fibrum két pontból áll, és a totális tér egy körvonal. És mi lehet a bázis, aminek a pontjaihoz tartoznak a „kétpontok”? Két pontot 180 fokkal elforgatva ismét ugyanezt a két pontot kapjuk, csak felcserélődnek. A bázis úgy állítható elő, hogy a 180 foknak megfelelő félkör két szélét összeragasztjuk. A bázis tehát egy kör. A fibrumot is lehet másképpen nevezni, ha figyelembe vesszük, hogy egy egyenesen egy adott ponttól egyenlő távolságra éppen két pont helyezkedik el. A gömbök meghatározása alapján tehát két pont az éppen a 0 dimenziós gömbfelület, ez tehát a fibrum. Íme hát a Hopf-fibrálás kistesója: a körvonal előáll, mint körvonalnyi sok „kétpont”, azaz nulla dimenziós gömbfelület.
 |
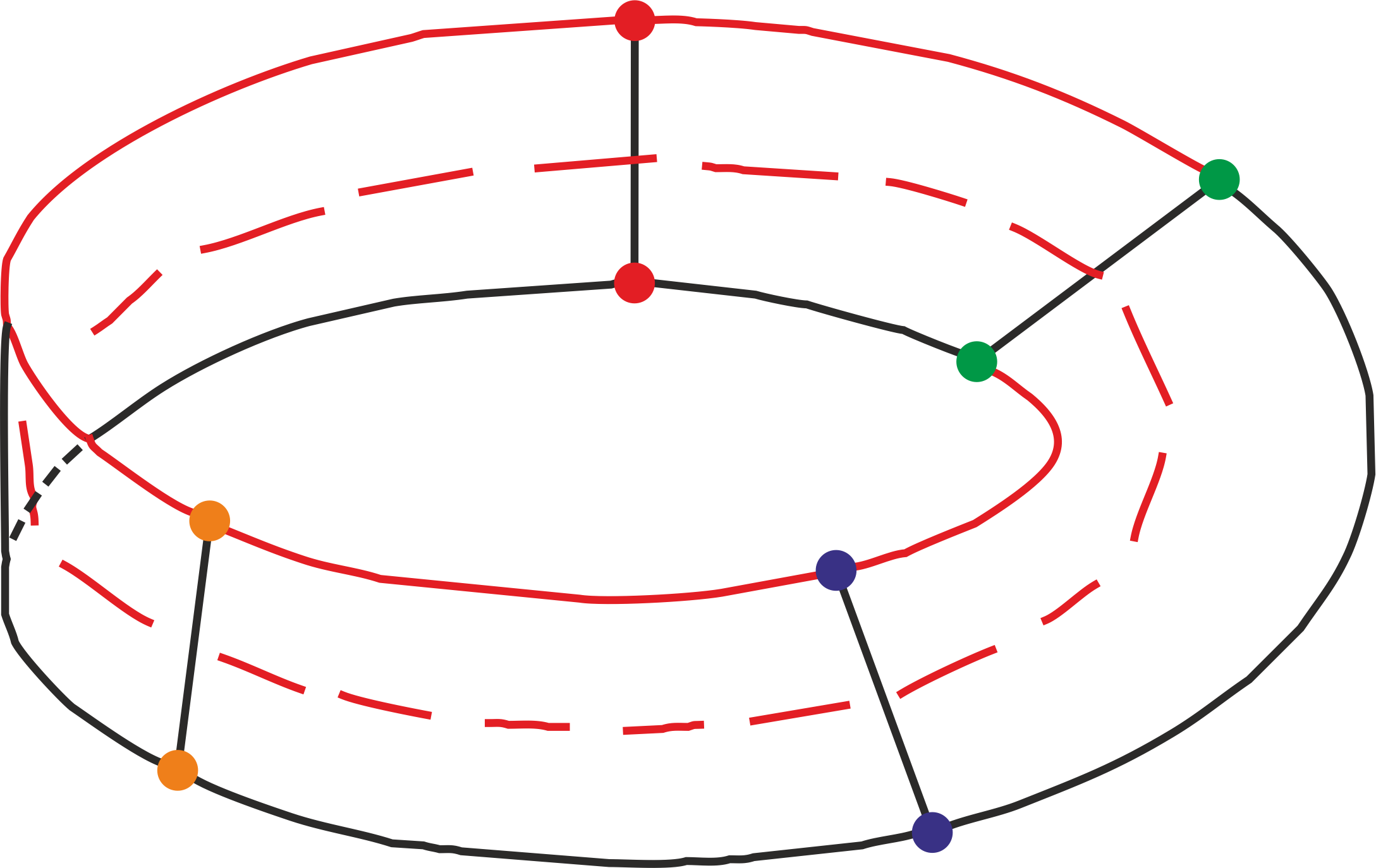 |
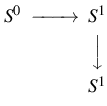
E nyaláb csavarodása a két pont felcserélődésében mutatkozik meg. Ezen a nyomon elindulva ráismerhetünk a nyaláb szemléletesebb alakjára. A totális tér a Möbius-szalag egyetlen peremköre, ami duplán kerüli meg a szalagot. A fibrumok a Möbius-szalag fibrumszakaszainak határpontjai, a báziskör pedig megfelel a Möbius-szalagot egyszer megkerülő középvonalnak. Ez a körvonal dupla fedése.
Az igazi Hopf-fibrálás pedig ugyanúgy származtatható, mint a kistestvére, csak valós számok helyett komplex számokkal kell csinálni: a Hopf-körök a komplex „síkon” a gömbnek és az origón átmenő komplex „egyeneseknek” a közös körei. A következőkben ezt nézzük meg, anélkül, hogy komplex számokról beszélnénk. Csak körülírjuk őket, szó szerint.
A négydimenziós tér pontjait 4 koordinátával adhatjuk meg. Magát a négydimenziós térbeli pontot ábrázolni nem tudjuk, bár lehetne próbálkozni például színezéssel, az utolsó koordináta az ábrázolt pont színét jelentené valamilyen színskálán. De ennél praktikusabb számunkra, ha két síkbeli pontként, illetve vektorként gondolunk rájuk. Tehát az ![]() pontot az
pontot az ![]() , illetve
, illetve ![]() síkbeli pontokkal jeleníthetjük meg, és praktikus mindkét ponthoz berajzolni az origóból egy mutatót is. A két ábrát rajzolhatjuk egymás mellé, vagy akár egy síkon is ábrázolhatjuk a kettőt, ők egy óra két mutatója. A négydimenziós tér pontjait ily módon két mutatóval tudjuk megjeleníteni, amik tudnak körbe forogni és a hosszúságuk is változhat. A négydimenziós térben az
síkbeli pontokkal jeleníthetjük meg, és praktikus mindkét ponthoz berajzolni az origóból egy mutatót is. A két ábrát rajzolhatjuk egymás mellé, vagy akár egy síkon is ábrázolhatjuk a kettőt, ők egy óra két mutatója. A négydimenziós tér pontjait ily módon két mutatóval tudjuk megjeleníteni, amik tudnak körbe forogni és a hosszúságuk is változhat. A négydimenziós térben az ![]() sík és a
sík és a ![]() sík egymásra merőleges síkok, és egyetlen közös pontjuk az origó. Úgy helyezkedik el egymáshoz képest a két sík, mint háromdimenziós térben egy sík és egy rá merőleges egyenes.
sík egymásra merőleges síkok, és egyetlen közös pontjuk az origó. Úgy helyezkedik el egymáshoz képest a két sík, mint háromdimenziós térben egy sík és egy rá merőleges egyenes.
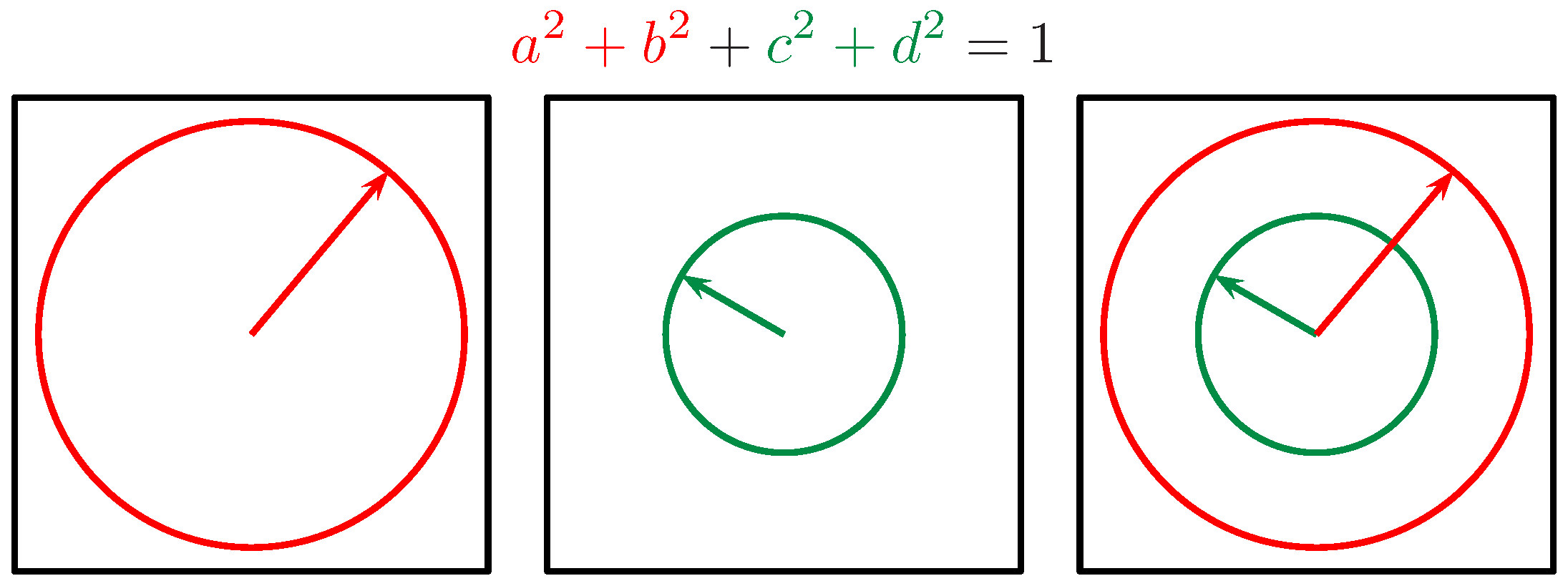
Mit jelent az, hogy a négydimenziós térbeli háromdimenziós gömbön vagyunk, praktikusan az origó körüli 1 sugarú gömbfelületen? Az ![]() pont távolsága az origótól 1, azaz
pont távolsága az origótól 1, azaz ![]() a Pitagorasz-tétel szerint, ami rendületlenül működik 4 dimenzióban is.
a Pitagorasz-tétel szerint, ami rendületlenül működik 4 dimenzióban is. ![]() éppen az első mutató hosszúságának a négyzete,
éppen az első mutató hosszúságának a négyzete, ![]() a másodiké. Tehát mindkét mutató hossza 0 és
a másodiké. Tehát mindkét mutató hossza 0 és ![]() között változhat, és ha az egyiket hosszabbra vesszük, a másik megrövidül éppen annyira, hogy a hosszaik négyzeteinek összege mindig 1 legyen.
között változhat, és ha az egyiket hosszabbra vesszük, a másik megrövidül éppen annyira, hogy a hosszaik négyzeteinek összege mindig 1 legyen.
Előfordulhat, hogy a második mutató hosszúsága nullává válik. Ekkor az első mutató hossza 1, befuthatja az egységkört, míg a másik mutató az origóban csücsül. És ugyanez fordítva: a második mutató az egységkörön mozoghat, míg az első az origóban kinullázódva pihen. Így kapunk két alapkört ![]() -ban, ezek a gömbnek az
-ban, ezek a gömbnek az ![]() síkon, illetve a
síkon, illetve a ![]() síkon fekvő körei. Ezek a Hopf-körök felelnek meg vetítés után a kiindulási körnek és a kijelölt egyenesnek a háromdimenziós térben. (A sztereografikus projekciót jellemzően az
síkon fekvő körei. Ezek a Hopf-körök felelnek meg vetítés után a kiindulási körnek és a kijelölt egyenesnek a háromdimenziós térben. (A sztereografikus projekciót jellemzően az ![]() vagy a
vagy a ![]() pontból szokás indítani, az első esetben az
pontból szokás indítani, az első esetben az ![]() , második esetben a
, második esetben a ![]() sík egységkörének az árnyéka nyúlik egyenessé.)
sík egységkörének az árnyéka nyúlik egyenessé.)
A két alapkört már megtaláltuk, most nézzük, mi van akkor, ha egyik mutató hossza sem 0! Ha az egyik mutató hosszát rögzítjük, az már meghatározza a másikét is. Így mindkét mutató a saját hosszúságának megfelelő sugarú körön tud mozogni egymástól függetlenül. Tehát a két mutató forgatása által bejárható ![]() pontok körvonalnyi sok körvonalat alkotnak, kétféleképpen is. Vagyis egy tóruszfelületet.
pontok körvonalnyi sok körvonalat alkotnak, kétféleképpen is. Vagyis egy tóruszfelületet.
Megtaláltuk hát a háromdimenziós térbeli ábrán egyre dagadó tóruszok eredetét a gömbben: ezek a rögzített hosszúságú első (és ez által meghatározott hosszúságú második) mutató által elkódolt pontok. Ahogy az első mutató hosszát növeljük, ez által a második mutató hossza csökken, így kapjuk a különböző tóruszokat. Ha az első mutató hossza nullává válik, a tórusz egyetlen körvonallá zsugorodik, míg a másik mutató nullává rövidülése a másik alapkört szolgáltatja. A tóruszok az egyik alapkörből indulnak ki és rászűkülnek a másik alapkörre, amint azt a háromdimenziós térbeli árnyékaikon is láttuk. Olyasmi ez, mint ahogy a kétdimenziós gömbfelület szélességi körei a pólusokban egyetlen ponttá zsugorodnak.
Megtaláltuk a két alapkört és a tóruszokat, keressük meg a többi kört, a tóruszokon ferdén futó köröket! Ha a két mutató egy rögzített állásából (azaz egy rögzített ![]() pontból) kiindulva az egyik mutatót körbeforgatjuk, úgy épp a tórusz meridiánját rajzoljuk ki, a másik mutató körbeforgatásával pedig a longitúdót. Hiszen a körvonalnyi sok körvonalként összeálló tórusz egy-egy alkotó körvonalán megyünk végig. (A meridián és a longitúdó a háromdimenziós térbeli tóruszfelületen különböznek egymástól, itt a négydimenziós térbeli gömbben azonban tökéletesen szimmetrikus a szerepük, csak hasraütésszerűen nevezem az elsőt meridiánnak, a másodikat longitúdónak.) Hopf-kört úgy kapunk, ha a meridiánon és a longitúdón is körbemegyünk egyszer, azaz ha mindkét mutatót egyszerre forgatjuk.
pontból) kiindulva az egyik mutatót körbeforgatjuk, úgy épp a tórusz meridiánját rajzoljuk ki, a másik mutató körbeforgatásával pedig a longitúdót. Hiszen a körvonalnyi sok körvonalként összeálló tórusz egy-egy alkotó körvonalán megyünk végig. (A meridián és a longitúdó a háromdimenziós térbeli tóruszfelületen különböznek egymástól, itt a négydimenziós térbeli gömbben azonban tökéletesen szimmetrikus a szerepük, csak hasraütésszerűen nevezem az elsőt meridiánnak, a másodikat longitúdónak.) Hopf-kört úgy kapunk, ha a meridiánon és a longitúdón is körbemegyünk egyszer, azaz ha mindkét mutatót egyszerre forgatjuk.
Összefoglalva, ha a két mutatót együtt forgatjuk, tehát az általuk bezárt szög nem változik, úgy egy Hopf-kört kapunk. Ha a két mutató egymástól függetlenül foroghat, az egy tórusz. Ha a hosszúságaikat is változtathatjuk úgy, hogy a hosszaik négyzetének összege mindig 1 maradjon, ez a háromdimenziós gömbfelület. Ha pedig bárhogy változtathatjuk mindkét mutató hosszát is, szögét is, a teljes négydimenziós teret kapjuk.
5. Qubit mint Hopf-fibrálás
A klasszikus digitális információ alapegysége a bit, aminek értéke lehet 0 vagy 1. Fizikailag ezt egy kétállapotú rendszer valósítja meg, praktikusan egy áramkörben átfolyik az áram (1) vagy sem (0). A kvantuminformatikában a bit megfelelője a qubit, egy kétállású kvantumrendszer. Ilyen például az elektron spinje, ami állhat egy adott irányban felfelé vagy lefelé. Hogy mi is az a spin, ezzel kapcsolatban egy mémet idéznék: „Képzelj el egy golyót, ami pörög. Csak ez nem golyó és nem pörög.” Hogy akkor mégis mi és mit csinál, arra a legőszintébb válasz a Hopf-fibrálás.
Egy kétállapotú kvantumrendszernek valójában végtelen sok lehetséges állapota van, amíg meg nem mérjük, és csak a mérés után ugrik be két állapot valamelyikébe. Híres hasonlat erre Schrödinger macskája[1], ami egy gondolatkísérlet a kvantumjelenség felnagyítására. Nem tudni, hogy a macska él-e vagy meghalt, amíg fel nem nyitjuk a dobozt. A rendszer állapotát első megközelítésben egy valószínűség írja le, pl. 30% annak valószínűsége, hogy a macska még él (az elektron spinje felfelé áll), és 70% annak, hogy meghalt (a spin lefelé áll). Ha megmérjük, rákérdezünk az állapotára, akkor ugrik csak be a 0 vagy 1 állapotok egyikébe.
De ez még mindig csak a jéghegy csúcsa! Egy ilyen rendszert teljes egészében két mutatóval lehet leírni, vagyis egy állapot a négydimenziós tér egy ![]() pontjával kódolható (ez felel meg a rendszer ún. hullámfüggvényének). A két mérés utáni állapot annak felel meg, amikor egyik vagy másik mutató hosszúsága nullává válik. A mutatók állásaiból kiolvashatjuk a valószínűségeket. A 0 állapot az, amikor a második mutató nullázódik ki, ennek valószínűsége az első mutató hosszának a négyzete,
pontjával kódolható (ez felel meg a rendszer ún. hullámfüggvényének). A két mérés utáni állapot annak felel meg, amikor egyik vagy másik mutató hosszúsága nullává válik. A mutatók állásaiból kiolvashatjuk a valószínűségeket. A 0 állapot az, amikor a második mutató nullázódik ki, ennek valószínűsége az első mutató hosszának a négyzete, ![]() . Az 1 állapotban az első mutató nullázódik ki, ennek valószínűsége a második mutató hosszának a négyzete,
. Az 1 állapotban az első mutató nullázódik ki, ennek valószínűsége a második mutató hosszának a négyzete, ![]() . De mivel csak ez a két lehetőség van, a két valószínűség összege 1 kell legyen, tehát
. De mivel csak ez a két lehetőség van, a két valószínűség összege 1 kell legyen, tehát ![]() . Ez azt jelenti, hogy a rendszer állapotát leíró
. Ez azt jelenti, hogy a rendszer állapotát leíró ![]() pontok éppen a háromdimenziós gömbfelület pontjai. Ha az egyik (és így mindkét) mutató hosszát rögzítjük, akkor az egyes állapotok valószínűségei már meghatározottak. A tóruszaink tehát az azonos valószínűségeket elkódoló állapotokat gyűjtik össze.
pontok éppen a háromdimenziós gömbfelület pontjai. Ha az egyik (és így mindkét) mutató hosszát rögzítjük, akkor az egyes állapotok valószínűségei már meghatározottak. A tóruszaink tehát az azonos valószínűségeket elkódoló állapotokat gyűjtik össze.
Azonban a globális fázis fizikailag nem releváns: ha a két mutatót együtt elforgatjuk, az állapotból kinyerhető információ nem változik. Így a fizikailag releváns információt a Hopf-körök hordozzák (ezeket írják le az állapotokhoz tartozó ún. sűrűségmátrixok). A Hopf-körök is elkódolják a valószínűségeket (hiszen az mutatók hosszúságát nem változtatjuk, egy tóruszon belül mozgunk), de ezen felül tartalmazzák az ún. relatív fázist is, azaz a két mutató által bezárt szöget (hiszen ez nem változik, ha együtt forgatjuk őket). A relatív fázis már fizikailag releváns, pl. más tengely irányú spin mérésénél nagyon is számít.
Ezért az állapotok, mint Hopf-körök a kétdimenziós gömbfelület pontjainak felelnek meg, hiszen ez a Hopf-fibrálás bázistere. Ebben a kontextusban az ![]() -et Bloch-gömbnek szokták nevezni.
-et Bloch-gömbnek szokták nevezni.
Amíg nem nézünk bele a dobozba, a macska állapota (az elektron spinje, fény polarizáltsága) egy gömbfelületen mozog, és minden állapot megfelel egy négydimenziós térbeli Hopf-körnek, ami fizikai realizálódás nélkül billeg a térben Schrödinger állapotegyenlete szerint. A mérés során a rendszer állapota „összeomlik”, realizálódik, beugrik az északi és a déli pólusnak megfelelő két alapkör egyikébe. Az elektron spinje esetén erre utal a szóhasználat: „felfelé” (azaz az északi pólus felé) vagy „lefelé” (a déli sark felé) áll.
Így függ össze tehát a koncerteken vetített vizuál, a Hopf-fibrálás, és a kvantumszámítógépek alapegység
[1] A macska hasonlat többjelentésű, lehet vele illusztrálni a kvantumösszefonódást is. E cikkben szándékosan csak a legegyszerűbb értelmezésével foglalkozom.










