Az elmúlt évek egyik legnagyobb riadalmat keltő járványa a 2015–2017-es dél-amerikai Zika-járvány volt. Bár a fertőzöttek túlnyomó többségénél a betegség tünetek nélkül, vagy igen enyhe tünetekkel zajlik le, a Zika mégis komoly veszélyt hordoz magában: kiderült ugyanis, hogy Zikával fertőzött nők magzatainál a betegség súlyos fejlődési rendellenességet, ún. kisfejűséget (mikrokefália) okozhat, illetve más neurológiai szövődmények is felléphetnek, különösen a Guillain–Barré-szindróma. A Zika-láz ezen kívül azért is veszélyesebb más, moszkitók által terjesztett betegségeknél (pl. dengue-láz, Chikungunya-láz), mert nemi úton is terjed.
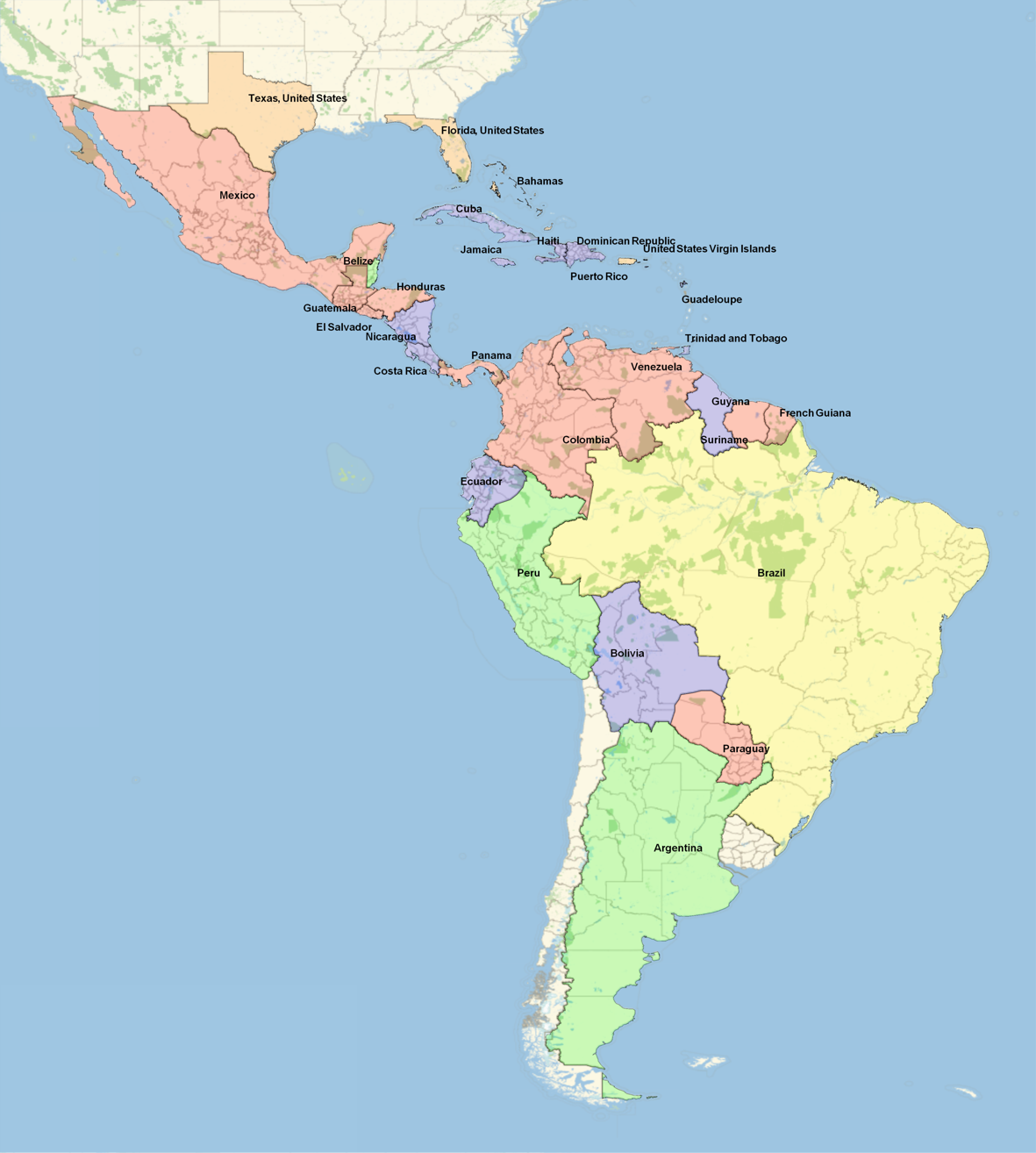
1. ábra. A Zika által érintett amerikai országok. A színek a betegség megjelenésének időpontját jelzik. Sárga: 2015. október előtt; rózsaszín: 2015. okt.–dec.; lila: 2016. jan.–márc.; zöld: 2016. ápr.–jún.; narancssárga: 2016. júl.–szept.
A dél-amerikai járvány kitörése után hamar megjelentek az első matematikai modellek is a betegség terjedésének leírására, a betegek számának, a járvány időtartamának előrejelzésére, a különböző paraméterek fontosságának becslésére. Sok más betegséghez hasonlóan a Zika-láz terjedését is leírhatjuk differenciálegyenleteket alkalmazó, ún. kompartment- vagy rekeszmodellek segítségével. Ez azt jelenti, hogy a népességet különböző osztályokba soroljuk aszerint, hogy a betegségnek melyik fázisában vannak – pl. fogékonyak, fertőzőek, felgyógyultak – és differenciálegyenletekkel írjuk le, milyen irányban, milyen dinamikával mozognak az emberek az egyes osztályok között. A modell pontosabbá tehető, ha egyéb szempontok – pl. kor, nem – alapján is megkülönböztetjük az embereket.
Az első, moszkitók által közvetített betegség leírására szolgáló modell Ronald Ross Nobel-díjas orvos nevéhez fűződik, aki a XX. század elején a malária terjedését írta le matematikai módszerekkel. Ross munkájában mind az emberek, mind a moszkitók populációját két részre – fogékonyak, illetve fertőzöttek – osztotta (ld. 2. ábra), és meghatározta a betegség terjedésében legnagyobb szerepet játszó paramétereket: a szúnyogcsípések számát, a fogékony lakosság méretét, a fertőző időszak hosszát. Ross a modell segítségével megmutatta, hogy létezik kritikus küszöbérték, amely alá csökkentve a szúnyogok létszámát a betegség visszaszorítható.
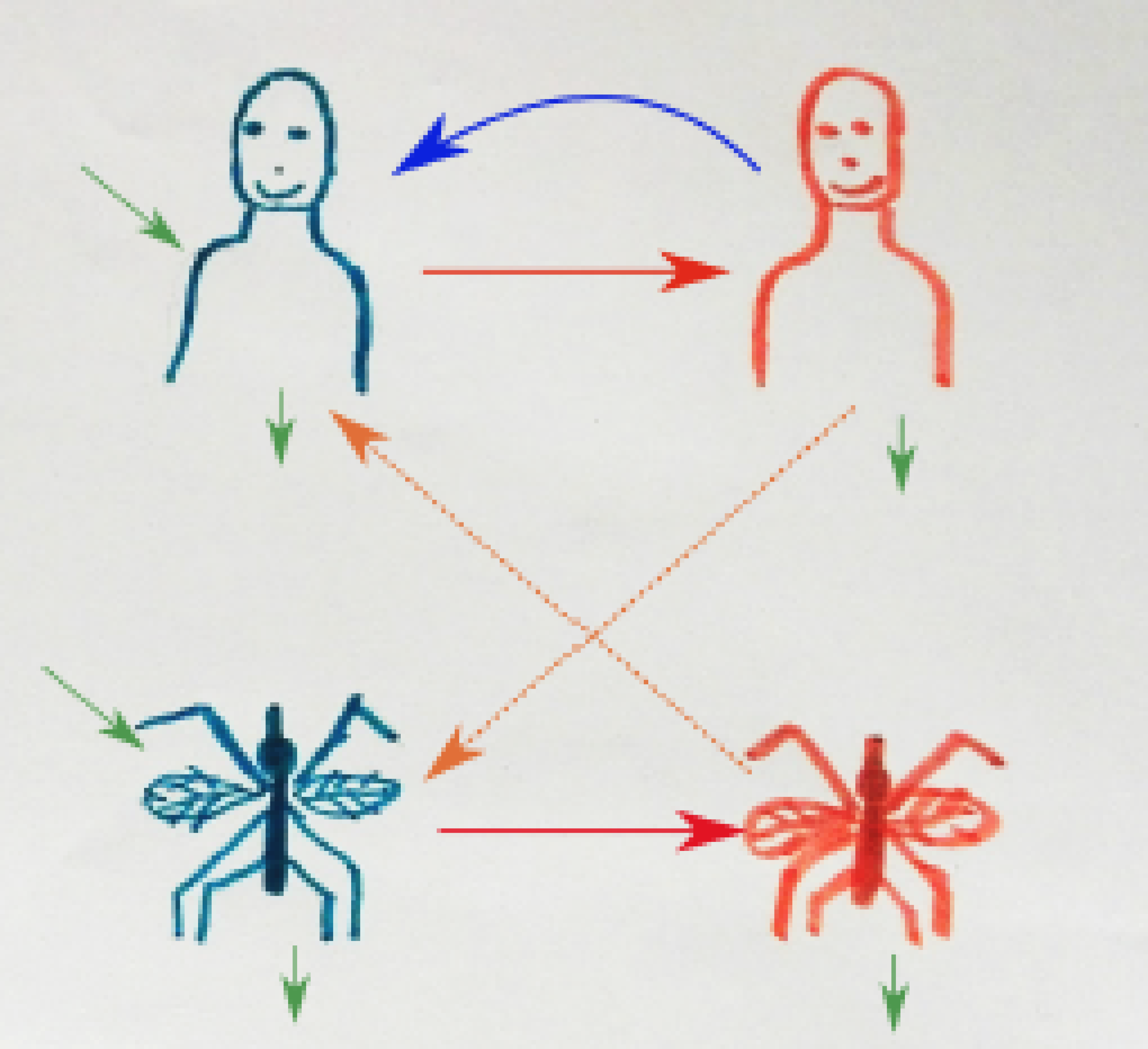
2. ábra. Ross modelljének folyamatábrája. Az ábráért köszönetet mondunk Röst Júliának.
A Ross-féle modell tulajdonképpen nemcsak a malária, hanem bármilyen, vektorok által terjesztett betegség modellje lehetne, hiszen az egyszerű modellben nem szerepelnek olyan tulajdonságok, amelyek csak a maláriára jellemzőek. Ez a modell tehát kiindulás lehet egy Zika-modell megalkotásához is. Hogyan tudnánk pontosabb modellt adni a Zika-láz terjedésére, amely magában foglalja a betegség egyedi jellemzőit is? Először is, figyelembe kell vennünk azt a tulajdonságot, amelyben a leginkább eltér a többi, moszkitók által terjesztett betegségtől, vagyis hogy a Zika nemi úton is terjed. Ezt többféleképpen is megtehetjük. Baca-Carrasco és Velasco-Hernández [1] a népességet a nemek szerint két részre osztották (ez nemi úton terjedő betegségek modellezésénél gyakran alkalmazott eszköz), és minden kompartmentet megdupláztak, vagyis modelljük a fogékonyakból, a fertőzöttekből és a felgyógyultakból is egy férfi és egy női osztályt tartalmaz, a két nem fertőzött képviselői az ellenkező nemű fogékonyakat fertőzhetik, amint azt a 3. ábrán láthatjuk.
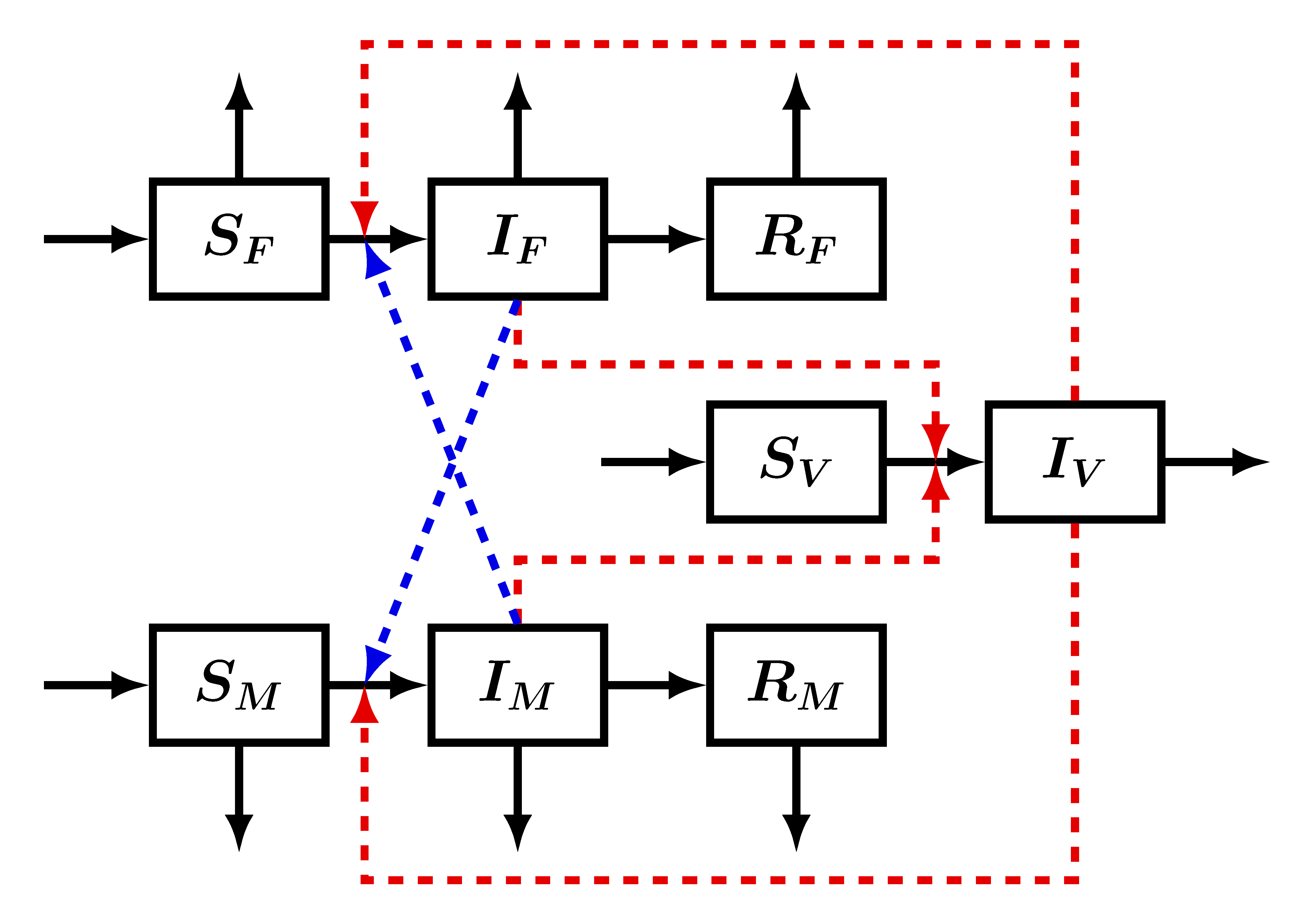
3. ábra. Baca-Carrasco és Velasco-Hernández modelljének folyamatábrája. Az ![]() indexek a nők, férfiak, illetve moszkitók populációját jelzik. A piros nyilak az emberek és vektorok közti átvitelt, a kék nyilak a nemi úton terjedést, a feketék pedig az egyes kompartmentek közti átmenetet jelzik.
indexek a nők, férfiak, illetve moszkitók populációját jelzik. A piros nyilak az emberek és vektorok közti átvitelt, a kék nyilak a nemi úton terjedést, a feketék pedig az egyes kompartmentek közti átmenetet jelzik.
Padmanabhan, Seshaiyer és Castillo-Chavez modelljében [4], a két nem nincs megkülönböztetve, de ez a modell is figyelembe veszi, hogy a betegség emberről emberre terjedhet (ld. 4. ábra). A szerzők a Zika egy másik fontos jellemzőjére is nagy hangsúlyt fektettek: a fertőzöttek nagy részre tünetmentes, azonban ők is továbbadhatják a betegséget akár a szúnyogokon keresztül, akár nemi úton. Ezért a modellben két fertőzött osztály szerepel, az egyikbe a tünetmenteseket, a másikba pedig a betegség tüneteit mutatókat soroljuk. A két csoportba tartozók megkülönböztetése igen fontos, hiszen amellett, hogy fertőzékenységük különbözhet, a viselkedésük is eltér, így egészen más valószínűséggel adhatják tovább a vírust. Fontos különbség az előző modellhez képest még az ![]() -vel jelölt látens osztályok bevezetése. Ide azok tartoznak, akik már megkapták a vírust, de ők maguk még nem fertőznek. A modell figyelembe veszi továbbá a rovarirtószerek használatát.
-vel jelölt látens osztályok bevezetése. Ide azok tartoznak, akik már megkapták a vírust, de ők maguk még nem fertőznek. A modell figyelembe veszi továbbá a rovarirtószerek használatát.
 4. ábra. Padmanabhan, Seshaiyer és Castillo-Chavez modelljének folyamatábrája. A
4. ábra. Padmanabhan, Seshaiyer és Castillo-Chavez modelljének folyamatábrája. A ![]() index az emberi, a
index az emberi, a ![]() pedig a moszkitókompartmenteket jelzi. Piros nyilak mutatják a betegség átadásának módjait.
pedig a moszkitókompartmenteket jelzi. Piros nyilak mutatják a betegség átadásának módjait.
Gao és társszerzői [3] szintén nem különböztették meg a két nemet, és az előzőekben ismertetett modellhez hasonlóan különválasztották a tünetmentes, illetve a tüneteket mutató fertőzötteket (![]() , ill.
, ill. ![]() ). Ebben a modellben azonban egy újabb osztályt vehetünk észre, ahová az
). Ebben a modellben azonban egy újabb osztályt vehetünk észre, ahová az ![]() osztályban lévők juthatnak. Az új kompartmentre azért volt szükség, mert kiderült, hogy a betegség még azután is hosszú ideig terjeszthető nemi úton, hogy a Zikával fertőzött személy felgyógyult a betegségből. Így, mielőtt egy fertőzött a teljes gyógyulást jelentő
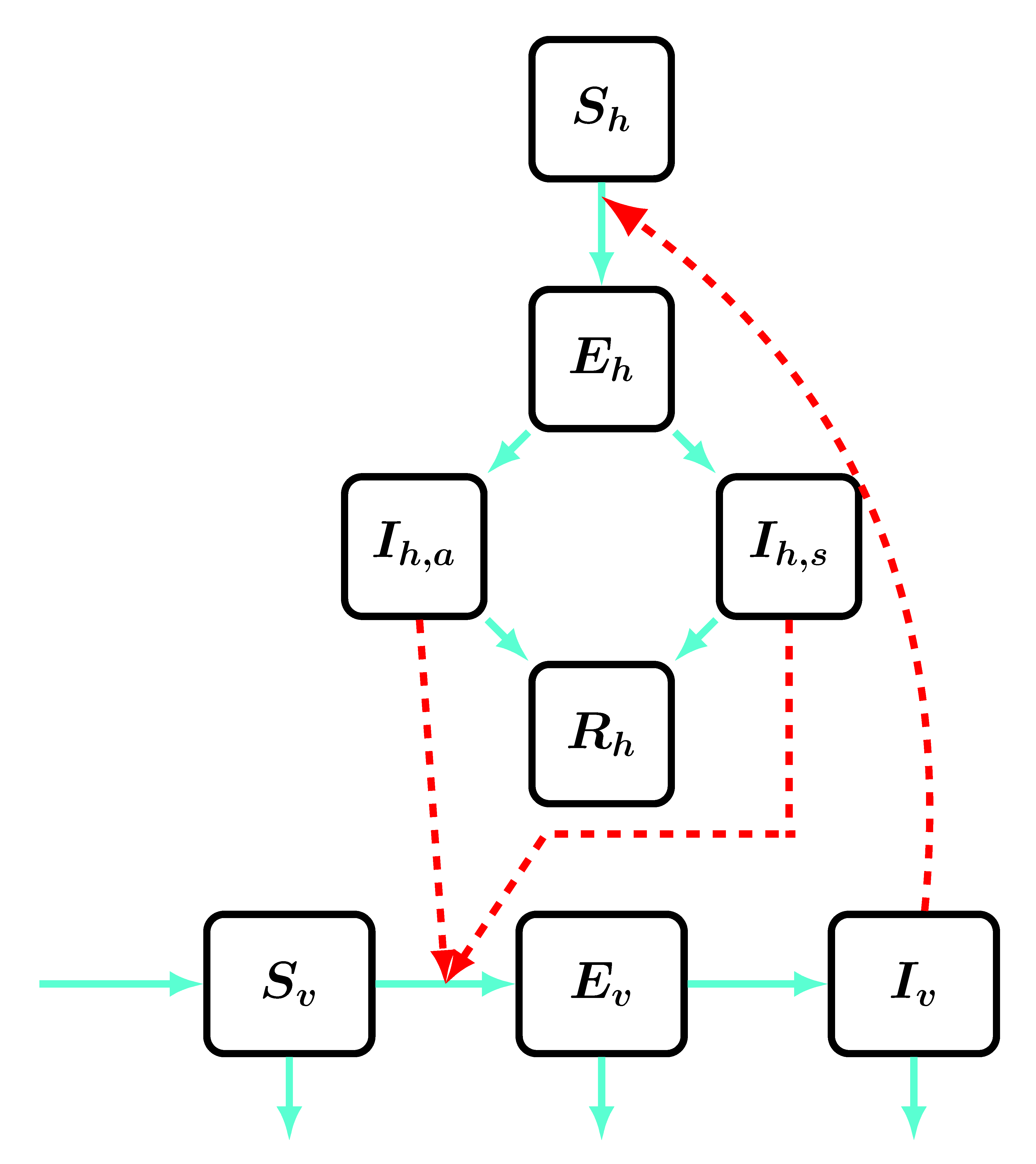
osztályban lévők juthatnak. Az új kompartmentre azért volt szükség, mert kiderült, hogy a betegség még azután is hosszú ideig terjeszthető nemi úton, hogy a Zikával fertőzött személy felgyógyult a betegségből. Így, mielőtt egy fertőzött a teljes gyógyulást jelentő ![]() osztályba jutna, átmenetileg ebbe a „lábadozó” osztályba kerül (ld. 5. ábra).
osztályba jutna, átmenetileg ebbe a „lábadozó” osztályba kerül (ld. 5. ábra).
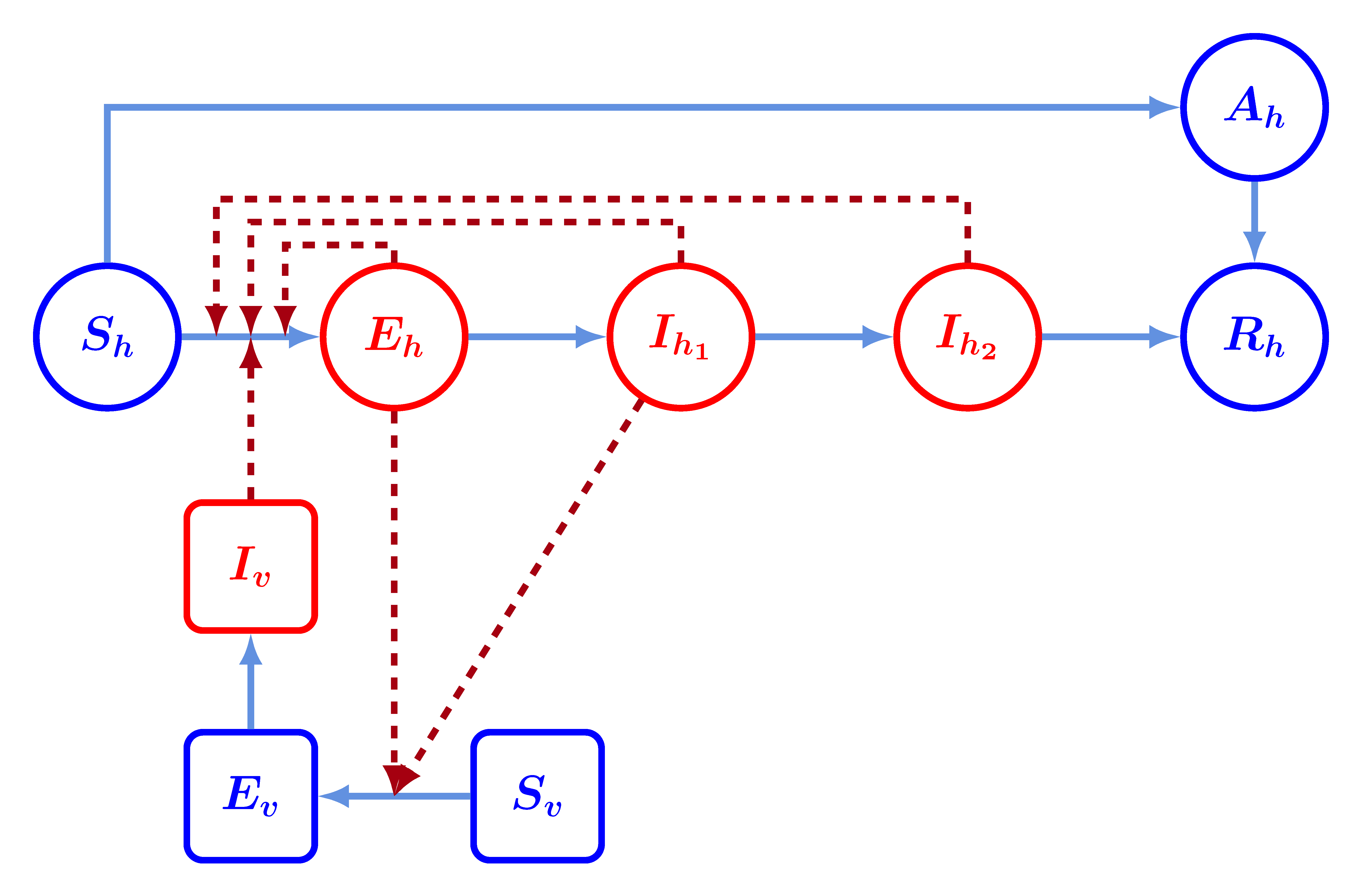
5. ábra. Gao és társszerzői modellje. Pirossal a fertőzött, kékkel az egészséges osztályokat jelöljük, a bordó nyilak a betegség átadásának lehetséges útjait, a kékek a kompartmentek közti mozgást jelzik.
Miután a szúnyogok elsődleges fontosságú szerepet játszanak a Zika-láz terjesztésében, a járvány alakulása természetesen nagymértékben függ e rovarok számától. A szúnyogpopuláció méretét az időjárás befolyásolja, így annak periodikus, évenkénti változását követve a moszkitók számában is hasonló szabályszerűséget vehetünk észre. A fenti modellek ezt nem vették figyelembe, a bennük szereplő paraméterek állandóak, ezért szegedi matematikusok olyan új modellt alkottak meg, amely időfüggő paraméterek segítségével az időjárás periodikus változását is magában foglalja. Az új modell pontosságát növeli ezen kívül, hogy a fenti modellekben szereplő jellemzőket is tartalmazza, vagyis megkülönbözteti a két nemet, szétválasztja a tünetmentes fertőzötteket és azokat, akiknél a tünetek jelentkeznek, továbbá figyelembe veszi, hogy a fertőzöttek nemi úton még felgyógyulásuk után is terjeszthetik a betegséget. Az új modell segítségével megmagyarázhatjuk, hogyan alakulhatott eltérő módon a járvány a különböző országokban és pontosabb előrejelzéseket adhatunk a járvány későbbi alakulására.
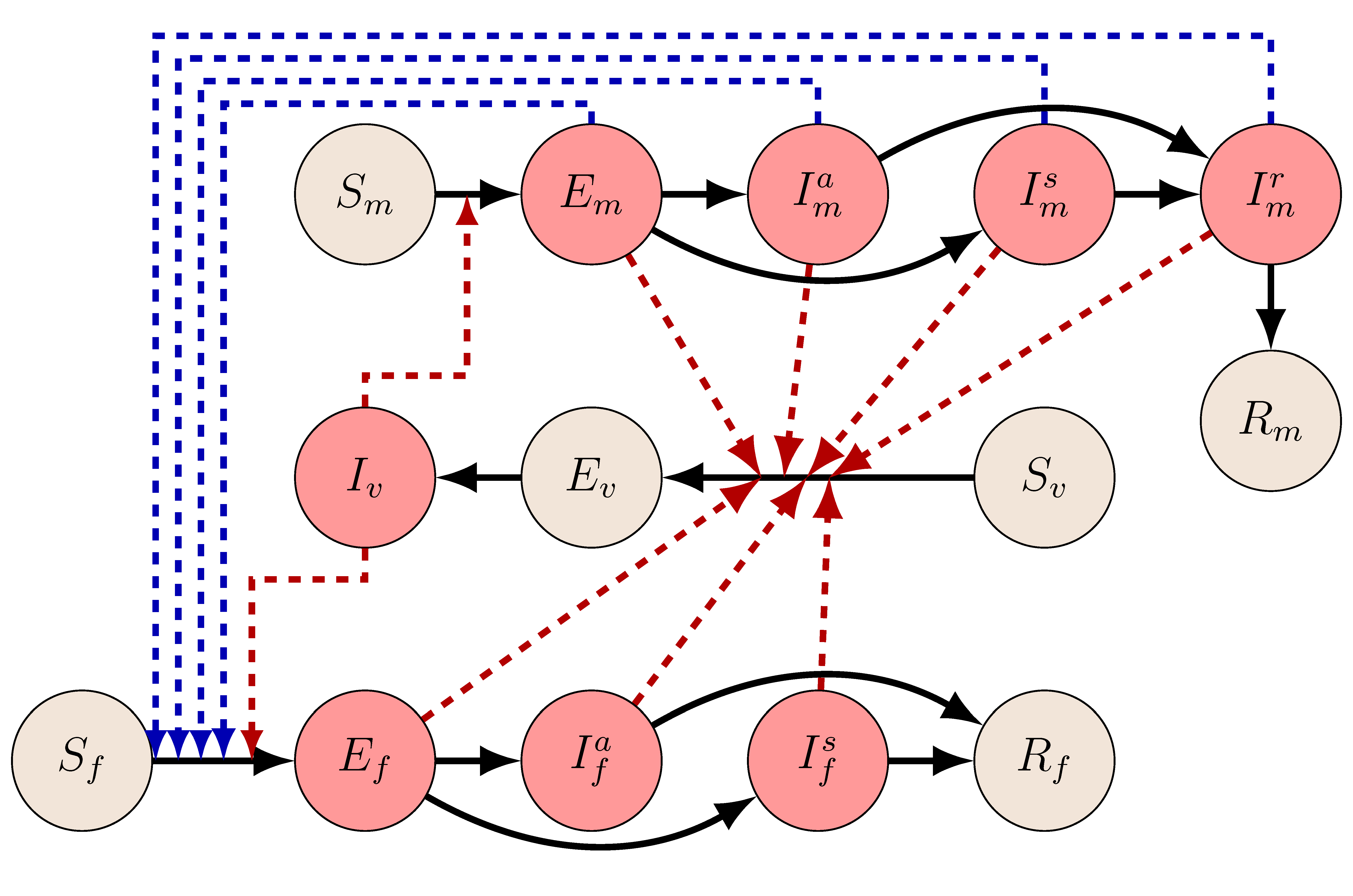
6. ábra. A szegedi kutatók Zika-modellje. A piros nyilak a moszkitóról emberre terjedés, a kékek az emberről emberre terjedés lehetséges módjait, a feketék pedig a kompartmentek közti mozgást mutatják.
Számos további módszer van arra, hogy a járványok terjedését leíró modelljeinket még pontosabbá tegyük. Parciális differenciálegyenletek segítségével leírhatjuk a betegség térbeli terjedését. Másik lehetőség több régió közti terjedés modellezésére, hogy a kompartmentjeinket „megsokszorozzuk” oly módon, hogy minden vizsgált régióban felírjuk az adott modellt, és az egyes területekre felírt differenciálegyenleteket a régiók közti utazással kapcsoljuk össze. Késleltetett differenciálegyenletek alkalmazásával modellezhetjük például a tünetek megjelenése előtti lappangó időszakot. Mindezek azt mutatják, a matematikai modellek továbbfejlesztésével egyre pontosabban írhatjuk le egy-egy járvány terjedését, figyelembe véve a betegség lehető legtöbb jellemzőjét. A modellek bonyolultabbá válásával persze matematikai vizsgálatuk is egyre nehezebb lesz, újabb és újabb matematikai eszközök kifejlesztésére van szükség, vagyis nem csak a matematika segíti a járványok elleni küzdelmet a pontosabb modellek, precízebb előrejelzések útján, hanem az új problémák felvetésével a járványtani kérdések is új kutatási irányok megszületését segítik elő a dinamikus rendszerek absztrakt matematikai elméletében.
Köszönetnyilvánítás

A cikk az Emberi Erőforrások Minisztériuma ÚNKP-18-4 Kódszámú Új Nemzeti Kiválóság Programjának támogatásával készült.
Irodalomjegyzék
- [1] D. Baca-Carrasco, J. X. Velasco-Hernández, Sex, mosquitoes and epidemics: an evaluation of Zika disease dynamics, Bull Math Biol. 78(2016), No. 11, 2228–2242.
[2] Dénes A., M. A. Ibrahim, L. Olouch, Tekeli M., Tekeli T., Impact of weather changes and sexual transmission on the spread of Zika fever, előkészületben.
[3] D. Gao, Y. Lou, D. He, T. C. Porco, Y. Kuang, G. Chowell, S. Ruan, Prevention and control of Zika as a mosquito-borne and sexually transmitted disease: a mathematical modeling analysis, Sci. Rep. 6(2016), 28070.
[4] P. Padmanabhan, P. Seshaiyer, C. Castillo-Chavez, Mathematical modeling, analysis and simulation of the spread of Zika with influence of sexual transmission and preventive measures, Lett. Biomath. 4(2017), No. 1, 148–166.
Szegedi Tudományegyetem, Bolyai Intézet









