A fertőző betegségek világméretű terjedését számos történelmi eset példázza. Az elmúlt húsz év jelentősebb járványai közt volt a 2002–2003-as SARS járvány, a 2009-es A(H1N1) influenza, majd a 2012-es közel-keleti MERS-vírus. Az Ebola-járvány 2013 és 2016 között pusztított Nyugat-Afrikában. A téma tehát mit sem veszít aktualitásából, a matematikai járványtan ennek okán az alkalmazott matematika egyik vezető jelentőségű területévé vált.
Természet- és műszaki tudományokban gyakran használunk ún. kompartment- (rekeszes) modelleket a fizikai rendszerek viselkedésének leírására. Egy járvány terjedésének modellezéséhez csoportokra osztjuk a populációt, és az egyes rekeszekben levő emberek számát az időben nyomon követve írjuk le a betegség terjedését. Feltételezzük, hogy a populáció homogén és az azonos csoporton belüli egyéneket nem különböztetjük meg. Így a csoportok közötti interakciót és mozgásokat figyelembe véve nemlineáris differenciálegyenleteket írhatunk fel az egyes rekeszekben levő emberek számának időbeni változására. A kompartment-modellek számos betegség terjedésének leírására alkalmasak, homogén (egy fertőzött csoport) és heterogén (több fertőzött csoport) populációkban, mind emberi, mind több fajt érintő (pl. szúnyog által terjesztett) járványokra. Metapopulációról és modelljeiről akkor beszélünk, amikor a populáció tagjai különböző térbeli helyszíneken tartózkodnak, amelyek között összeköttetés van.
A járványmodellezés egyik legfontosabb kérdése annak meghatározása, hogy a betegség képes-e elterjedni egy fogékony populációban, vagy rövid idő alatt kihal. Meg kell vizsgálnunk, hogyan függ a dinamika az egyes modellparaméterektől, majd az egyes paraméterekre küszöböt adva leírhatjuk a betegségmentes altér határait. Ezek a kérdések nehéz matematikai problémákat jelentenek, különösen a bonyolult sokdimenziós modellekben. Az emberek mobilitását korlátozó kontrollstratégiák vizsgálata különösen összetett. Egy betegségmentes területet megvédhetünk a beutazás meggátolásával, ugyanakkor egy ilyen intézkedés negatív hatással lehet a rendszer más részeire; az egyes régiókban való utazási korlátozás más területeken nagyobb csoportosulást idézhet elő, ami magasabb betegszámhoz és a járvány gyorsabb terjedéséhez vezet.
A metapopulációs modellek felhasználhatósága sokrétű a matematikai biológiai kutatások terén. A matematikai analízisből nyert eredmények figyelembevételével a járványügyi hatóságok hatékonyabb betegségkezelési és védekezési stratégiákat állíthatnak fel. Az egyik legegyszerűbb rekeszes modell az SIRS-modell (S: fogékony, I: fertőzött, R: felgyógyult), amelynek metapopulációs változatában vizsgálhatjuk a védőoltás, a kontaktszám csökkentése, és a különböző területek közötti utazást korlátozó stratégiák hatását. Az eredmények kiterjeszthetők arra az esetre is, amikor az utazási korlátozás csak a populáció egyes csoportjaira alkalmazható.
Az Egyesült Államokban a hepatitis-B járványok kapcsán figyelték meg azt az érdekes jelenséget, miszerint a megbetegedések száma jelentős eltérést mutathat a különböző városok között. Ez matematikai nyelvre lefordítva annyit tesz, miszerint a járványterjedés dinamikáját leíró rendszernek több stabil egyensúlyi állapota is van. Az ilyen járványok lefolyását előrejelezni, és a védekezési stratégiát felállítani különösen nehéz feladat a többféle lehetséges egyensúlyi állapot miatt.
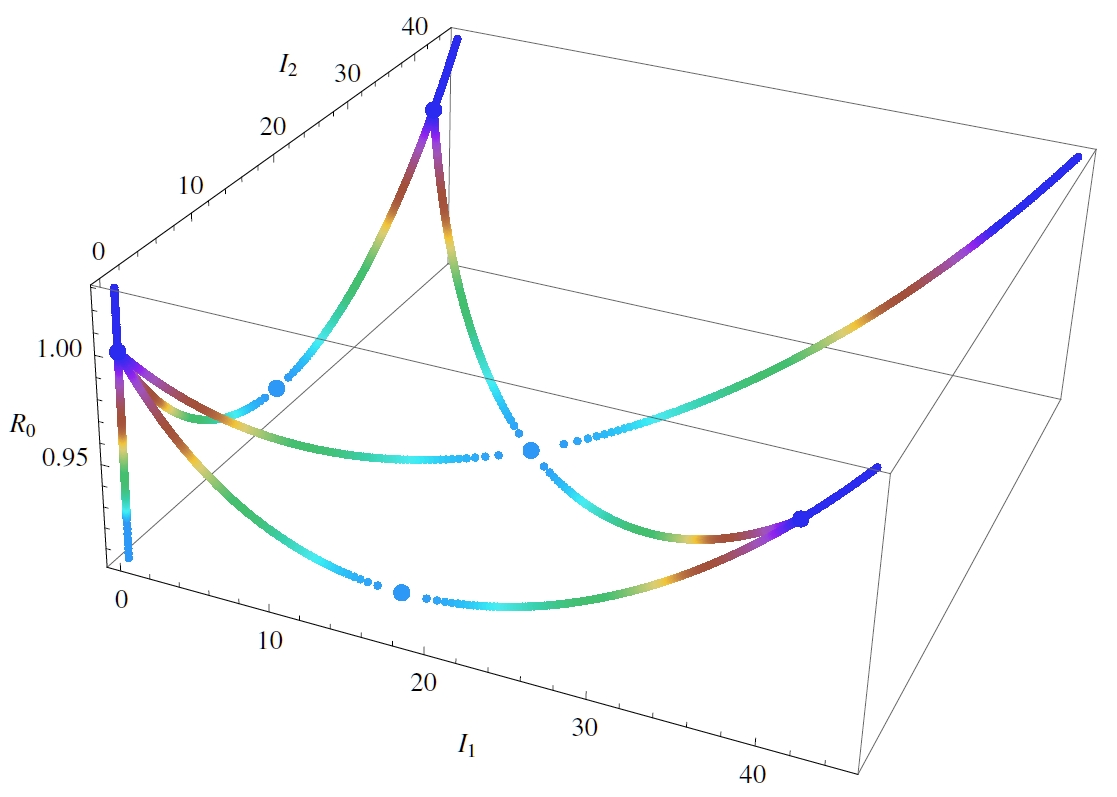
Az ábra egy olyan szituációt ábrázol, amikor két régió áll összeköttetésben, és mindkét helyen egy tökéletlen védőoltással vakcinálunk.A tökéletlenség azt jelenti, hogy a védőoltás nem mindenkinek ad védelmet, illetve csak részleges védelmet biztosít. A színes görbék a lehetséges egyensúlyi helyzeteket jelzik, ahol I1 és I2 jelenti a fertőzöttek számát a két régióban, a függőleges tengelyen pedig egy fontos paraméter, az alap reprodukciós szám változik, amellyel az egyensúlyok (az ábrán a színes görbék vízszintes síkokkal vett metszéspontjai) száma is megváltozhat, ezt nevezzük bifurkációnak. A bifurkációs pontokat a nagyobb méretű pontok jelzik. A háromdimenziós bifurkációs diagram egy érdekes rája-szerű alakzatot rajzol ki, a tanulsága pedig az, hogy a térbeli struktúra miatt a dinamika sokkal komplexebbé válhat.
Tekintsünk egy SIVS–típusú (fogékony–fertőzött–vakcinált–fogékony) modellt két összekapcsolt régióra. Az egy régióra megszorított, háromdimenziós rendszerben bistabilitás léphet fel bizonyos paramétertartományokban: három egyensúlyi helyzet közül kettő is lehet stabil, egy betegségmentes és egy endemikus állapot. A számítógépes szimulációkkal segített matematikai analízis rendkívül gazdag bifurkációs struktúrát fed fel a modellben: az összekapcsolt régiókra felírt rendszernek akár kilenc egyensúlyi helyzete is lehet, amelyek tripla transzkritikus, illetve dupla nyereg-csomó bifurkációs pontokban jelennek meg.
A metapopulációs modellek nem csak ember és ember között terjedő, hanem szúnyogok által terjesztett betegségek modellezésére is alkalmasak. A dengue-láz, a chikungunya-láz és a malária három olyan, világszerte pusztító betegség, amit szúnyogok terjesztenek. Ezeknek a járványoknak a dinamikáját számos tényező befolyásolja: a betegségterjedés két, egymástól jelentősen különböző tulajdonságokkal bíró populáció (emberek, szúnyogok) interakciójával jön létre, valamint a dinamikára térbeli tényezők (pl. szúnyogok helyváltoztatása) is hatással vannak. E betegségek modelljei kevés módosítással alkalmassá tehetők kullancsok által terjesztett járványok leírására, ilyenek Magyarországon és Európa-szerte megbetegedéseket okoznak emberekben és állatokban. A dengue-láz elsődleges védekezési stratégiái a szúnyogokat célozzák. Számos kontrollprogram van használatban világszerte, mint például a szúnyogok irtása illetve a sterilrovar-technika. Ezek a stratégiák a rovarfejlődési ciklus különféle szintjein hatnak, és általában helyszínspecifikusak is (a steril rovarokat kijelölt helyen engedik el), tehát részletes matematikai modellre van szükség. A jelenleg fejlesztés alatt álló vakcina képes lehet csökkenteni a megbetegedések számát, ugyanakkor több tanulmány is figyelmeztet a védőoltás negatív hatásaira egyes korcsoportokban. Ebben a bonyolult járványtani kérdésben tehát kiemelt jelentőséget kap a betegségmodellezés és a kontrollstratégiák kvalitatív analízise.
Számos biológiai folyamat dinamikájában megfigyelhetők nemautonóm hatások. A dengue-láz terjesztéséért felelős szúnyogpopuláció mérete ciklikusan változik a szezonális dinamikának megfelelően. A népszerű nyaralóhelyek forgalma ugyancsak nagy különbségeket mutat az év különböző részeiben, a járványkitörés valószínűsége jóval nagyobb, ha egy fertőzött utazó főszezonban érkezik.
A fent leírt bistabilitás jelensége nemcsak járványterjedési modellekben léphet fel. A szakirodalomban sokat idézett Allee–effektus Warder Clyde Allee nevéhez fűződik, aki egy 1931-ben közölt írásában egy aranyhal-populáció növekedését vizsgálva kis denzitásokon fellépő negatív denzitásfüggést figyelt meg. Más szóval, kis populációméret esetén az egyedeknek hátrányt jelent társaik hiánya, ami korlátozott (gyakran negatív) növekedést jelent a populációra nézve. Ekkor megadható egy kritikus szint a populáció méretére (Allee–határ): ez alatt a populáció hosszú távon kihal, azonban a populáció képes lehet a növekedésre, ha mérete meghaladja a kritikus értéket. A matematika nyelvére lefordítva ez azt jelenti, hogy minden, az Allee–határ mint egyensúlyi helyzet alatt indított megoldás a triviális egyensúlyhoz konvergál (kihalás, üres populáció), az Allee–határállapotnál nagyobb kezdeti értékekkel viszont nő a populáció, míg el nem éri annak eltartóképességét (pozitív, stabil állapot). Metapopulációs modellekkel állati populációk migrációs viselkedésének hatását is vizsgálhatjuk. Ha a vándorlás helyszíneire, mint régiókra tekintünk és feltesszük, hogy az egyes szubpopulációkban Allee–jelenség léphet fel, akkor egy metapopulációs modellhez jutunk. Ezekkel a kutatásokkal matematikai úton magyarázatot nyerünk arra az állati populációkra megfigyelhető jelenségre, miszerint a populációk egyedszáma jelentősen különböző a populáció élőhelyei között.
Knipl Diána
Megj. A szerzőről többet tudhat meg ebből a cikkből. (A szerk.)









