A közgazdaságtan matematikai elméletében szokásos a befektetők pénzhez való viszonyát ún. hasznossági függvényekkel jellemezni. Egy ilyen ![]() függvény
függvény ![]() értéke azt fejezi, ki hogy az adott befektető mennyire elégedett
értéke azt fejezi, ki hogy az adott befektető mennyire elégedett ![]() forinttal, mennyi hasznot jelent számára ez az összeg, szubjektív értelemben.
forinttal, mennyi hasznot jelent számára ez az összeg, szubjektív értelemben.
Az ![]() függvény jellemző tulajdonságai vita tárgyát képezik. Abban talán mindenki egyetért, hogy
függvény jellemző tulajdonságai vita tárgyát képezik. Abban talán mindenki egyetért, hogy ![]() folytonos (hiszen kis változás a vagyoni helyzetben csak kis mértékben változtatja meg az elégedettség szintjét), és monoton növő (több pénznek jobban örülünk). Mi mostantól feltesszük, hogy
folytonos (hiszen kis változás a vagyoni helyzetben csak kis mértékben változtatja meg az elégedettség szintjét), és monoton növő (több pénznek jobban örülünk). Mi mostantól feltesszük, hogy ![]() szigorúan monoton növő és folytonosan differenciálható.
szigorúan monoton növő és folytonosan differenciálható.
Még egy fontos jellemző tulajdonság lehet, hogy ![]() konkáv, ez a feltevés azonban már vitatható, amint azt alább részletesebben kifejtjük. Már Daniel Bernoulli úttörő [1] cikkében is konkáv
konkáv, ez a feltevés azonban már vitatható, amint azt alább részletesebben kifejtjük. Már Daniel Bernoulli úttörő [1] cikkében is konkáv ![]() szerepelt. Ezt a tulajdonságot a befektetők kockázatkerülő magatartásával szokás magyarázni: egy kis
szerepelt. Ezt a tulajdonságot a befektetők kockázatkerülő magatartásával szokás magyarázni: egy kis ![]() csökkenés a vagyonban
csökkenés a vagyonban ![]() -szel csökkenti a hasznosságot. Ha
-szel csökkenti a hasznosságot. Ha ![]() konkáv, akkor
konkáv, akkor ![]() csökkenésével ez a mennyiség egyre nő, azaz az elégedettség egyre gyorsuló ütemben csökken. Különösen igaz ez a 0 (= csőd) közelében, ezért általában olyan
csökkenésével ez a mennyiség egyre nő, azaz az elégedettség egyre gyorsuló ütemben csökken. Különösen igaz ez a 0 (= csőd) közelében, ezért általában olyan ![]() -t használnak, melyre
-t használnak, melyre ![]() ,
, ![]() , például
, például ![]() valamely
valamely ![]() ,
, ![]() számra, vagy
számra, vagy ![]() .
.
Egyelőre tegyük fel, hogy ![]() konkáv (a későbbiekben majd tárgyalunk egyéb eseteket is). Nézzük meg, hogyan tűzhető ki az optimális befektetési feladat az adott hasznossági függvénnyel bíró piaci szereplő számára!
konkáv (a későbbiekben majd tárgyalunk egyéb eseteket is). Nézzük meg, hogyan tűzhető ki az optimális befektetési feladat az adott hasznossági függvénnyel bíró piaci szereplő számára!
A lehetséges portfólió stratégiák halmazát célszerű egy ![]() vektortérrel leírni (mely általában végtelen dimenziós és valamely topológiával is el van látva). A vektortér struktúra annak felel meg, hogy ha
vektortérrel leírni (mely általában végtelen dimenziós és valamely topológiával is el van látva). A vektortér struktúra annak felel meg, hogy ha ![]() portfóliók kereskedhetők, akkor általában azok egyesítése
portfóliók kereskedhetők, akkor általában azok egyesítése ![]() is, valamint valós konstansszorosa is, tehát
is, valamint valós konstansszorosa is, tehát ![]() minden
minden ![]() -re. Negatív
-re. Negatív ![]() azt jelenti, hogy az adott portfóliót nem vesszük, hanem eladjuk, erre sok piacon van lehetőség. A
azt jelenti, hogy az adott portfóliót nem vesszük, hanem eladjuk, erre sok piacon van lehetőség. A ![]() portfólió ára
portfólió ára ![]() , kézenfekvő feltenni, hogy
, kézenfekvő feltenni, hogy ![]() lineáris függvény. Az adott
lineáris függvény. Az adott ![]() portfólió hozama a
portfólió hozama a ![]() valószínűségi változó (hiszen a legtöbb befektetés bizonytalan kimenetelű). A
valószínűségi változó (hiszen a legtöbb befektetés bizonytalan kimenetelű). A ![]() hozzárendelés is lineáris. Ha a befektetőnek
hozzárendelés is lineáris. Ha a befektetőnek ![]() kezdeti tőkéje van, akkor olyan portfóliók közül választhat, melyekre
kezdeti tőkéje van, akkor olyan portfóliók közül választhat, melyekre ![]() teljesül. Ha a
teljesül. Ha a ![]() befektetés mellett dönt, akkor vagyona
befektetés mellett dönt, akkor vagyona ![]() -ről
-ről ![]() -re változik.
-re változik.
Csak azokat a befektetéseket engedjük meg, melyek a csődöt elkerülik, ezért a megengedett portfóliók halmaza
Ez ![]() -nek konvex részhalmaza.
-nek konvex részhalmaza.
Az adott piaci szereplő célja, hogy ezek közül kiválassza a számára legmegfelelőbbet. Az optimális befektetési feladat tehát így fogalmazható meg: keressük azt a ![]() befektetést, melyre
befektetést, melyre
azaz ![]() -vel jelölve a várható érték operátort, a várható hasznosság a
-vel jelölve a várható érték operátort, a várható hasznosság a ![]() stratégiát követve lesz a legnagyobb. Itt valójában feladatok egy családjáról beszélhetünk, amit a
stratégiát követve lesz a legnagyobb. Itt valójában feladatok egy családjáról beszélhetünk, amit a ![]() paraméterez.
paraméterez.
A feladat helyesen kitűzött, ha ![]() minden
minden ![]() -ra. Láthatóan konkáv funkcionálokat kell maximalizálni egy (topologikus) vektortér valamely konvex részhalmazán. Mivel
-ra. Láthatóan konkáv funkcionálokat kell maximalizálni egy (topologikus) vektortér valamely konvex részhalmazán. Mivel ![]() többnyire végtelen dimenziós, az ilyen
többnyire végtelen dimenziós, az ilyen ![]() létezésének bizonyítása nem egyszerű feladat, még konkrét modellek esetében sem.
létezésének bizonyítása nem egyszerű feladat, még konkrét modellek esetében sem.
A probléma abban rejlik, hogy ha pl. ![]() egy Banach-tér,
egy Banach-tér, ![]() pedig annak korlátos részhalmaza (általában még csak nem is korlátos!), akkor sem kompakt a normatopológiában. Tehát, ha
pedig annak korlátos részhalmaza (általában még csak nem is korlátos!), akkor sem kompakt a normatopológiában. Tehát, ha ![]() egy sorozat, melynek mentén az (1)-ben szereplő a szuprémum eléretik, akkor nem feltétlenül lehet belőle konvergens részsorozatot kiválasztani!
egy sorozat, melynek mentén az (1)-ben szereplő a szuprémum eléretik, akkor nem feltétlenül lehet belőle konvergens részsorozatot kiválasztani!
Természetesen léteznek ügyes technikák a nehézségek leküzdésére. Példaképpen az alábbi fontos tételt idézzük.
Tétel. (Komlós János, [4]) Ha ![]() egy valószínűségi mező,
egy valószínűségi mező, ![]() ,
, ![]() pedig valószínűségi változók olyan sorozata, amelyre
pedig valószínűségi változók olyan sorozata, amelyre ![]() , akkor van olyan
, akkor van olyan ![]() ,
, ![]() részsorozat és egy
részsorozat és egy ![]() valószínűségi változó, amelyre
valószínűségi változó, amelyre
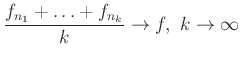
fenáll a ![]() -majdnem mindenütt konvergencia értelmében.
-majdnem mindenütt konvergencia értelmében.
Azaz kiválasztható majdnem mindenütt értelemben Césaro-konvergens részsorozat. Ehhez hasonló eredmények számos topologikus vektortérben ismeretesek: egy megfelelő értelemben korlátos sorozatnak vannak olyan konvex lineáris kombinációi (a fenti tételben átlagai), amelyek konvergálnak.
Ha tehát a fentebb említett ![]() sorozat alkalmas értelemben korlátos (ez rendszerint következik abból, hogy aszimptotikusan optimális stratégiákat tekintünk), akkor valamely
sorozat alkalmas értelemben korlátos (ez rendszerint következik abból, hogy aszimptotikusan optimális stratégiákat tekintünk), akkor valamely
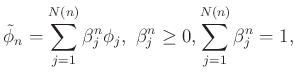
konvex lineáris kombinációi konvergálnak valamely ![]() stratégiához (egy alkalmas topológiában), itt
stratégiához (egy alkalmas topológiában), itt ![]() a konvex kombinációk tagszáma,
a konvex kombinációk tagszáma, ![]() pedig a konvex súlyok. (Ehhez persze kell az is, hogy
pedig a konvex súlyok. (Ehhez persze kell az is, hogy ![]() zárt legyen a tekintett topológiában.)
zárt legyen a tekintett topológiában.)
Mivel ![]() konkáv,
konkáv, ![]() ,
, ![]() lineárisak,
lineárisak,
ezért a ![]() stratégiák várható hasznossága továbbra is az (1)-beli-beli szuprémumhoz tart. Ezek után remélhető (de messze nem nyilvánvaló), hogy a
stratégiák várható hasznossága továbbra is az (1)-beli-beli szuprémumhoz tart. Ezek után remélhető (de messze nem nyilvánvaló), hogy a ![]() stratégia eléri a szuprémumot, tehát optimális lesz.
stratégia eléri a szuprémumot, tehát optimális lesz.
Az imént vázolt gondolatmenet közvetlenül általában nehezen alkalmazható a pénzügyi matematika modelljeiben. Segít azonban a lineáris programozásban is használatos duális probléma bevezetése. A jelen esetben ez a következő problémacsaládhoz vezet: minden ![]() -ra keressük azt az
-ra keressük azt az ![]() -et, amelyre
-et, amelyre
teljesül. Itt ![]() ,
, ![]() az
az ![]() Fenchel-Legendre konjugáltja,
Fenchel-Legendre konjugáltja, ![]() pedig (nagyjából) a
pedig (nagyjából) a ![]() anullátora, vagyis
anullátora, vagyis
ahol ![]() egy olyan
egy olyan ![]() topologikus vektortér duális tere, mely tartalmazza a
topologikus vektortér duális tere, mely tartalmazza a ![]() halmazt.
halmazt.
A fenti elvont leírást talán jobban megvilágítja egy konkrét példa. Ha például egy részvénnyel kereskedünk, akkor ![]() (nagyjából) azonosítható azon
(nagyjából) azonosítható azon ![]() valószínűségi mértékek halmazával, melyekre nézve a részvényárfolyamat martingál.
valószínűségi mértékek halmazával, melyekre nézve a részvényárfolyamat martingál.
Általában viszonylag könnyű igazolni, hogy a duális problémának van megoldása, amiből (1) megoldása egy explicit transzformációval megkapható (persze mindez a modelltől függő, cseppet sem egyszerű meggondolásokat igényel). Igazolható az is, hogy a ![]() függvény az
függvény az ![]() Fenchel-Legendre konjugáltja, illetve a primál/duál problémák közötti szokásos összefüggések is bizonyíthatók.
Fenchel-Legendre konjugáltja, illetve a primál/duál problémák közötti szokásos összefüggések is bizonyíthatók.
A duális problémán alapuló megoldási módszer először [5]-ben lett részletesen kidolgozva. Ez az elegáns és hatékony megközelítés azonban nem mindig működik. Például ha bizonytalan a ![]() mérték, csak annyit tudunk róla hogy valószínűségi mértékek egy
mérték, csak annyit tudunk róla hogy valószínűségi mértékek egy ![]() családjába esik, akkor modellbizonytalanság áll fenn, és célszerű (1) helyett inkább az
családjába esik, akkor modellbizonytalanság áll fenn, és célszerű (1) helyett inkább az
problémát tekinteni. Ez jóval nehezebb, és ismert, hogy duális problémájának nincsen mindig megoldása. Ilyen és hasonló okok rákényszerítenek arra, hogy (3) megoldását közvetlenül, a duális problémát mellőzve találjuk meg.
Ilyen eredmények először [7]-ben bukkantak fel ![]() -en definiált
-en definiált ![]() -ra. Nagyon fontos azonban
-ra. Nagyon fontos azonban ![]() hasznossági függvényeket is vizsgálni, ezekkel elemezhető a veszteségek hatása is:
hasznossági függvényeket is vizsgálni, ezekkel elemezhető a veszteségek hatása is: ![]() esetén
esetén ![]() a befektető „csalódottságának” mértéke. Az ilyen
a befektető „csalódottságának” mértéke. Az ilyen ![]() -k használatán számos kockázetelemzési módszer alapul. Ilyenkor az (1) feladat nehezebb (és persze a stratégiák
-k használatán számos kockázetelemzési módszer alapul. Ilyenkor az (1) feladat nehezebb (és persze a stratégiák ![]() osztályát is módosítani kell). Közvetlen, a duális problémát elkerülő megközelítést sikerült adnunk [6]-ben, mely a fenti Komlós tétel egy új, [2]-ból származó változatán alapszik. A felhasznált topologikus vektorterek az ún. Orlicz-terek, melyek a funkcionálanalízisből jól ismert
osztályát is módosítani kell). Közvetlen, a duális problémát elkerülő megközelítést sikerült adnunk [6]-ben, mely a fenti Komlós tétel egy új, [2]-ból származó változatán alapszik. A felhasznált topologikus vektorterek az ún. Orlicz-terek, melyek a funkcionálanalízisből jól ismert ![]() terek általánosításai.
terek általánosításai.
A [3] cikk szerzői kísérletekkel támasztották alá, hogy a befektetők ![]() hasznossági függvénye ún. „S-alakú”: valamely
hasznossági függvénye ún. „S-alakú”: valamely ![]() -ra konvex a
-ra konvex a ![]() és konkáv a
és konkáv a ![]() intervallumokon. (Ezért 2002-ben Kahnemann közgazdaságtani Nobel-díjat kapott.) Ilyenkor a duális probléma értelmét veszti, és a Komlós tétel változatai sem használhatóak (mert (2) nem igaz). Ilyen esetekben teljesen más módszerek szükségesek és csak kevés eredmény ismeretes.
intervallumokon. (Ezért 2002-ben Kahnemann közgazdaságtani Nobel-díjat kapott.) Ilyenkor a duális probléma értelmét veszti, és a Komlós tétel változatai sem használhatóak (mert (2) nem igaz). Ilyen esetekben teljesen más módszerek szükségesek és csak kevés eredmény ismeretes.
A téma iránt mélyebben érdeklődőknek a [8] könyv 7. fejezete ajánlható (a megfelelő előismeretek elsajátítása után), illetve a [7] jegyzet is jól olvasható.
Rásonyi Miklós
MTA Rényi Alfréd Matematikai Kutatóintézet
Irodalomjegyzék
[1] D. Bernoulli. Exposition of a new theory on the measurement of risk. Econometrica, 22:23—36, 1954. (Az 1738-ban megjelent latin eredeti angol fordítása.)
[2] F. Delbaen, K. Owari. Convex functions on dual Orlicz spaces. arXiv:1611.06218
[3] D. Kahnemann, A. Tversky. Prospect theory: An analysis of decision under risk. Econometrica, 47:263—291, 1979.
[4] J. Komlós. A generalization of a problem of Steinhaus. Acta Mathematica, 18:217—229, 1967.
[5] D. Kramkov, W. Schachermayer. The condition on the Asymptotic Elasticity of Utility Functions and Optimal Investment in Incomplete Markets. Annals of Applied Probability, 9:904—950, 1999.
[6] M. Rásonyi. On optimal investment without passing by the dual problem. arXiv:1702.00982
[7] W. Schachermayer. Portfolio Optimization in Incomplete Financial Markets. Notes of the Scuola Normale Superiore Cattedra Galileiana, Pisa, 2004. Letölthető a http://www.mat.univie.ac.at/~schachermayer/pubs/index.php honlapról a [116]-os publikáció.
[8] H. Pham. Continuous-time Stochastic Control and Optimization with Financial Applications, Springer, 2009.
Fotó: https://www.pexels.com/photo/u-s-dollar-bills-pin-down-on-the-ground-164474/










![$\displaystyle u(c):=\sup_{\phi\in\mathcal{A}(c)}E[U(c-p(\phi)+Z(\phi))]=E[U(c-p(\phi^*)+Z(\phi^*))],$](/images/stories/latex/rasonyimiklosoptimalisbefektetesek/img32.png)
![$\displaystyle E[U(c-p(\tilde{\phi}^n)+Z(\tilde{\phi}^n))]\geq \sum_{j=1}\beta^n_j E[U(c-p(\phi_n)+Z(\phi_n))],$](/images/stories/latex/rasonyimiklosoptimalisbefektetesek/img53.png)
![$\displaystyle u(c):=\sup_{\phi\in\mathcal{A}(c)}\inf_{P\in\mathcal{P}}E_P[U(c-p(\phi)+Z(\phi))],$](/images/stories/latex/rasonyimiklosoptimalisbefektetesek/img70.png)