Információk

 Aktuális szám: 4. szám 2017. június 

Szükséges, elégséges, lehetséges — Mennyi matek kell egy kognitív tudományi mesternek?

Szükséges, elégséges, lehetséges — Mennyi matek kell egy kognitív tudományi mesternek?

 

Bevezetés

Körülbelül tíz évvel ezelőtt Bádog tanár úr, alias (cybersznoboknak aka) Pléh Csaba akadémikus, miután 2004-ben megalapította a BME Kognitív Tudományi Tanszékét, mesterszak alapításába fogott. Ennek részeként nyilván saját meggyőződéséből fakadóan, de a műszaki egyetemi környezet hatására is úgy gondolta, matematikai tárgyakra (beleértve ebbe az informatikát is) szükség lenne a képzés részeként. Ezek kidolgozásához a vele folytatott konzultációk után fogtam hozzá.

Kognitív tudomány

Magam számára azt a definíciót találtam ki, hogy ez a tudomány (egyesek szeretik többes számba tenni) úgy jött létre, hogy miután a biológia, csillagászat, fizika és társai kiszabadultak a filozófia fogságából, az ismeretelmélet is ezt szeretné tenni. (A kedves kollégák elég jól viselik ezt a definíciót.) Mérésekkel, kísérletekkel, modellekkel megközelíteni a tudás megszerzésének, tárolásának, feldolgozásának folyamatát a korábbi elmélkedés (hogy ne mondjam, introspekció, azaz önmegfigyelés) helyett.

A képzés célja

Először nyilván meg kell határozni a képzés célját. Ha jól vettem ki, a tanároké az volt, hogy a doktori iskola számára képezzünk hallgatókat, egységes stabil tudásszintre hozva a legkülönbözőbb területekről érkező embereket, remélve azonban, hogy a sokféle előismeret a közös munka folyamán majd előnyökkel is fog járni. Visszatekintve úgy látom, hogy a hallgatók jelentős része azért jött hozzánk, hogy (akár munka mellett) mester szintű diplomát szerezzen, néha megfejelve a kevéssé kiváló helyen szerzett BSc/BA fokozatát. Nem elhanyagolható azok száma sem, akik semmilyen érdeket nem tartottak szem előtt, csak érdeklődést: passzióból végzik el (munka mellett) a négy félévet.

Másutt mi van

Rendszeres és alapos áttekintés helyett néhány benyomásom következik.

Először is: matematika és kognitív tudomány kapcsolatára keresve a neten elsősorban olyan munkákat találunk, amelyek arról szólnak, hogy mit tud a második adni az elsőnek. De tárgyunk most nem ez. Lássuk néhány intézmény képzését.

A Central European University-n tanítanak statisztikát, beleértve a kísérlettervezést is, továbbá játékelméletet. Programozás címén a MATLAB és a Python szerepel.

A New York University kurzusa rendkívül gazdag statisztikában, és óriási pozitívuma, hogy alaposan (ki)használják a számítógépet, még ha csak a MATLAB-ot is. Számomra viszont elképzelhetetlen, hogy az analízis alapjai nélkül vágnak bele például a Fourier-transzformált ismertetésébe.

Irvine-ben (University of California) körülbelül hasonló a kötelező anyag, mint nálunk, de BSc szinten. Továbbá (annak ellenére, hogy) a képzés a társadalomtudományi karon zajlik (megjegyzendő, hogy a mi képzésünk is ott indult), nagyon sok a kötelezően választható matematikai jellegű tárgyak száma, amelyek közül a diáknak kell néhányat választania.

Ha jól látom, a Budapest Semester in Cognitive Science különálló matematikai tárgyat nem tartalmaz, de modellekről bőven esik szó, nyilván feltételezhetők a hallgatókról alkalmas előismeretek.

Kedvencem persze ez:

Here's my list of math subjects that support the study of brain (from a computational neuroscientist's perspective):

  • Linear algebra
    • to understand high dimensions, to compute things quickly, foundation for other math
  • Calculus
    • basics for everything continuous valued
  • Statistics
    • to analyze any data, you need stats!
    • basis for modeling, regression, clustering, classification, and all
  • Differential equations (basis for dynamical system)
  • Dynamical system
    • intuition for neural dynamics (deterministic approximation)
    • modeling single neuron, synapse, small network
  • Statistical physics
    • modeling large scale noisy neural dynamics
  • Information theory
    • quantify how much "information" is coded in neural signal
  • Numerical computation
    • your data and algorithm needs to be implemented in a computer
  • Convex optimization
    • your statistics/model requires optimization
  • Probability theory (basis for stochastic process and statistics)
  • Stochastic process
    • model of neural signals, decision process (diffusion), basis for advanced statistics
    • point process theory is useful for dealing with neural spike trains
  • Time series analysis (your data is a time series!)
  • Signal detection theory
    • psychophysics is often designed to be a detection task

Brain is quite noisy, you need tools to deal with noise. More applied math than pure math is needed.

I have only seen topology being used a handful of times, and they were not very useful nor impressive. I love set theory and mathematical logic, but sadly never used it nor seen it being used.

In addition, real/complex/functional analyses are also useful, just in general.

Alig többet sorol fel, mint amit egy matematikus öt év alatt kellene, hogy megtanuljon. Igaz, hogy nem az oktatandó anyag, hanem a tudomány jelenlegi állásának áttekintése kapcsán, de nagyjából ugyanilyen sok mindent sorol fel Andler (2012) is. Ő még a kategóriaelméletet is kiemeli, amely talán Piaget és társai (1990) hatására lett oly népszerű a kognitív tudományban.

Tervek

Lássuk tehát először is a terveket, majd a megvalósulást.

Három tantárgyat terveztünk, $ 2+2$ óra matematikát, 2 óra statisztikát és $ 2+2$ óra informatikát. A későbbiekben ezeknek az óraszámoknak módosítását javasoltam: az informatikára 2 óra maradt, a statisztika óraszáma $ 2+2$-re módosult.

Matematika

A Matematika tárgy tartalma a természettudományos és műszaki egyetemeken szokásos első félévi tematika töredéke: azt szeretném elérni, hogy eljussunk a derivált fogalmának legfőbb alkalmazásáig: a függvényvizsgálatig. Menet közben viszont meglehetősen sokat (többet, mint a mérnök hallgatóknál) foglalkozunk a matematika felépítésével, logikával, bizonyítási módszerekkel, és amikor csak lehet, színes történeti és filozófiai megjegyzésekkel szórakoztatjuk a hallgatókat. Azt szeretnénk ugyanis elérni, hogy kedvük legyen a tárgyhoz, és hogy meglássák a számukra közvetve vagy közvetlenül hasznos elveket, módszereket. Általában azt gondolom (Tóth, 2001), hogy az egyetemen nehéz elméletet kell tanulni, mert ha ez elmarad, azt később sokkal több energiába kerül elsajátítani. Itt ezt a meggyőződésemet zárójelbe teszem.

Gyakorlatok

A gyakorlatokon meglehetősen kevés időt szánunk a deriválási szabályok begyakorlására, viszont olvasnivalókat osztunk szét a hallgatók közt, amiről azután beszámolnak.

Kedvenc feladatsorunk a természetes nyelvi mondatok formalizálása, például az ilyeneké (a szerzőket az idézetek alapján könnyen megtalálhatjuk a neten):

If you want a lover,

I'll do anything you ask me to

And if you want another kind of love,

I'll wear a mask for you

If you want a partner, take my hand

Or if you want to strike me down in anger,

Here I stand

I'm your man

Vagy egy régebbről származó kedvenc:

If you can talk with crowds and keep your virtue,   

    Or walk with Kings—nor lose the common touch, 

If neither foes nor loving friends can hurt you, 

    If all men count with you, but none too much; 

If you can fill the unforgiving minute 

    With sixty seconds’ worth of distance run,   

Yours is the Earth and everything that’s in it,   

    And—which is more—you’ll be a Man, my son!

 

Avagy ilyeneké, ahol már nem úszhatjuk meg a kvantorokat:

You can fool all the people some of the time, and

some of the people all the time, but

you cannot fool all the people all the time.

 

Legyen egy magyar is:

Vagy bolondok vagyunk s elveszünk egy szálig,
Vagy ez a mi hitünk valóságra válik.

 

Ja, miért is angol idézeteket soroltam? Mert az eredeti, kőbe ugyan nem vésett elképzelés szerint a képzés nagyobbik része angol nyelven folyik. Korábban azt gondoltuk, hogy 95%-a, de ez ingadozik (lefelé). Például jobbat tesz a hallgatóknak, ha a matematika gyakorlatai magyar nyelven zajlanak. Tipikus, hogy a záróvizsgán az angolul írt diplomamunkájukat angolul ismertetik a hallgatók, míg a szakmai kérdésekre magyarul válaszolnak. Ez se tökéletes megoldás, mert tanulmányaik során az angol szaknyelvet sajátítják el.

Arra is felhívjuk a hallgatók figyelmét, hogy az elemi logikai műveletek és a kvantorok használata a matematika számára ugyan általában elegendő, de messze nem elégséges a hétköznapi nyelv számára. Ennek igazolásaként nagy örömmel loptam el Cseresnyési Lászlótól (2016) az alábbi példát:

Mari megcsókolta Julit, annyira örült.
Mari megcsókolta Julit, annyira sírt.

 

(Ki is az alanya a második tagmondatnak?)

Ami a függvényvizsgálatot illeti, ott fő példáink a normális eloszlás sűrűségfüggvénye, két exponenciális függvény különbsége, egy exponenciális és egy trigonometrikus szorzata — mind közvetlenül hasznosítható. Az ezt közvetlenül megelőző témakörből megemlítem kedvenc példámat. A szélsőérték-számítás egyszerűbb feladatai után érdemes megoldani azt a feladatot, hogy közelítsük az $ (x_{1}y_{1}),(x_{2}y_{2}),\ldots,(x_{n}y_{n})$ mérési pontokat origón átmenő egyenessel. 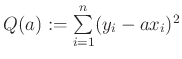Ehhez minimalizálni kell a $ Q(a):=\sum\limits_{i=1}^n (y_{i}-ax_{i})^{2}$ függvényt, ami a $ Q$ egyváltozós függvény stacionárius pontjának meghatározását jelenti, majd annak belátását, hogy ez a pont minimum. A feladat előkészíti a lineáris regressziót, amelynél a megfelelő kétváltozós függvény minimumának meghatározása már gondot szokott okozni.

Előadások

Módszerünk a frontális ismeretközlés. Viszont mielőtt szónokolni kezdek, mindig iratok egy kis röpdolgozatot az előző óra definícióiból. Közhely, hogy matematikát és nyelvet úgy lehet tanulni, hogy mindig, minden részletét mozgósítjuk. Az is ismeretes, hogy egy vegyészt nem engednek be gyakorlatra, ha nem ismeri a gyakorlat anyagát. Ennek analógiájára én is úgy gondolom, hogy az üljön be az órámra, aki minimális szinten követi az anyagot. A röpike elvesz egy kis időt az órából, ki is kell javítani (vagy inkább gyorsan pontozni kell), de állandóan éberségre készteti a hallgatókat, továbbá katalógusként is szolgál. Közönséges (például villamosmérnököknek vagy informatikusoknak tartott) gyakorlatokon is ezt műveltem. Szerettek J. Azok a kollégák nem kevésbé, akik túlmunkát élvező sztahanovisták.

Még egy apróság: soha nem tartom egyben a két 45 perces órát, hogy legyen módjuk a hallgatóknak is egymással ismerkedni, és én is tudjak velük beszélgetni.

Jegyzet

Mindig készülőben. Ugye, itt (mint majdnem mindenütt) az a csapda, hogy ha van jegyzet, akkor miért kellene előadásra járni, ha pedig nincs, akkor ez a súlyos hiányosság az előadó szemére vethető.

Vizsga

A vizsgán egyrészt az előadások és gyakorlatok matematikaanyagáról kell beszámolni egy tételjegyzék alapján. Ebből a részből az érdekel, hogy áttekintése van-e az egészről a hallgatónak, ebben az értelemben szigorlathoz jobban hasonlít.

A másik rész pedig beszámoló egy műről. Előre kiadok egy listát, ahol klasszikusok szerepelnek, ld. néhány példát a hivatkozások között (Hodgkin-Huxley, Arbib-Érdi-Szentágothai, Abbott, Neumann, Bush). Ezek közül a hallgató kiválaszt ötöt, és ezzel a szűkített listával és olvasmányonként két-két általa megfogalmazott kérdéssel jön a vizsgára, ahol én választok ki egyet, hogy ismertesse. A klasszikus irományok mellett lehet előadást választani a TED-ről, vagy majdnem akármit, majdnem akárhonnan, de azért legyen valami köze a matematikához és a kognitív tudományhoz. Örömmel tudtam meg, hogy a művek közül néhányat a Kognitív Tudományi Tanszék is ajánl különféle kurzusokon.

A gyakorlaton szerzett pontszámok nagy súllyal szerepelnek az értékelésben, amit azért hangsúlyozok, mert van, ahol ezeket kizárólag annak eldöntésére használják, hogy mehessen vizsgára a hallgató, de évközi teljesítményének mennyiségét és minőségét pedig semmire.

Statisztika

Az egyetemek természettudományos és műszaki szakjain az a szokás, hogy félév alatt, heti két órában eljutnak a kockadobástól a lineáris regresszióig, amit egy statisztikus csak borzadállyal szemlélhet, de ezeket az órákat kénytelen megtartani. Nálunk természetesen nemcsak a mértékelmélet hiányzik ahhoz, hogy matematikai statisztikát tanítsunk, de a mi matematikaóránkon még az integrálás sem tud előkerülni. A sok rossz megoldás közül most a számítógép gombjainak nyomogatása dívik. Az eredmény a diplomamunkában szereplő mérések és kísérletek elemzésénél ragyog fel igazán L.

Ami különlegesen fontos lenne, az annak tudatosítása, hogy a statisztikai módszerek alkalmazásának feltételei vannak, a számszerű eredmények pedig csak a számok jelentésének ismeretében interpretálhatóak értelmesen.

Informatika

Kétség sem merülhetett föl, hogy a Wolfram nyelv (leánykori nevén: Mathematica) elemeivel megismertetjük a hallgatókat. Itt most csak nagyon röviden érvelek emellett. Felépítése hihetetlenül egységes és átgondolt, azon kívül, hogy mindegyik programozási stílus használható benne, saját stílusa meglehetősen gazdaságos. Használható fekete dobozként, vagy szimbolikus kalkulátorként, de leáshatunk az algoritmusok mélyére is. A benne foglalt algoritmusok és adatok (!) mennyisége, hm, jelentős. (Az ötödik változat leírása 3000 oldal volt, a mostani 11-esé 50000 oldal lenne, ezért már kizárólag elektronikus formában létezik a kézikönyv.)

Korábban próbálkoztunk a szokásos, axiomatikusnak mondható felépítéssel: megbeszéltük a szintaxis részleteit, a programozás elemeit, az adatstruktúrákat, stb. Újabban azzal kísérletezünk, hogy belevágunk: a hallgatók számára érdekes feladatok (kép- és szövegfeldolgozás) megoldását mutatjuk meg. Ilyen szellemben készült Lóczi Lajos és Sándor Nóra (2014) jegyzete. A félév végére viszont elvárjuk, hogy a hallgatók önállóan (bár kis csoportokban) készítsenek egy értelmes programot és arról kiselőadásban számoljanak be.

Egyetlen példát említek: a (biológus előképzettségű) hallgató társastáncot is oktatott. Nehezen tudta elmagyarázni tanítványainak, hogyan váltsanak alakzatot tánc közben, hogyan formáljanak kört egyenesből stb. Készített egy animációt azzal, hogy a továbbiakban azt fogja használni. Nyilvánvaló, hogy máskor is képes lesz használni a programot bármilyen kutatási feladatához is.

Kapcsolatok

Az eddigiekből is látható, amit külön hangsúlyozni szeretnék: ezeknek a tárgyaknak még egymáshoz is van közük! Rendszeresen megemlítem, hogy a Wolfram nyelv mely függvényei használhatók az analízisben és a statisztikában. Volt olyan évfolyam, ahol valamennyire sikerült megvalósítani, hogy mindhárom tárgyban támaszkodjunk a Wolfram nyelvre. Meggyőződésem, hogy mesze a leggazdaságosabb megoldás ez, hosszú távú előnyökkel együtt.

A hallgatók

Ha valaki azt gondolná, hogy csak móka és kacagás itt az oktatás, annak hadd álljon itt néhány szak, amit diákjaink előzőleg elvégeztek: amerikanisztika, angol, általános iskolai tanár, biológia, farmakológia, filozófia, finn, fizika, gazdasági matematika, gyógypedagógia, informatika, kognitív tudomány (Angliában, ugyanis Magyarországon nincs alapképzés), konduktor, magyar, pénzügy, pszichológia, szociológia, tájtervező, történelem. (Érdekes, hogy matematikus végzettségű hallgatónk még nem volt.)

A félév elején a következőket szoktam megkérdezni: milyen szako(ka)t végzett, hol, milyen szinten. (Félévben mérve) mennyi matekot, statisztikát, informatikát tanult. Ha valaki két vagy több félévet tanult egyetemi szinten, annak az előadások látogatását nem tiltom meg, de számukra csak a zárthelyik megírása kötelező, illetve a vizsga. (Komolynak látszó előismerettel is szerepelt már rosszul hallgató.) Kicsit több a nő, mint a férfi. Az életkor becslésem alapján 21 és 55 között változik.

Előadásaimat (nem csak itt) azzal szoktam zárni a félév végén, hogy később, akár sok év múlva is megkereshetnek a hallgatók, amikor olyan problémájuk akad, amelyikben segíthetek. Viszont mi is sok segítséget kaptunk már tőlük: amikor sajókazai diákokat láttunk vendégül, elsőként a kognitív szakos hallgatók ugrottak, hogy segítenek. Van olyan hallgató, aki már az oktatásban segít, megint mással ismeretterjesztő cikket írattunk stb.

Az oktatók

Egy normális/tipikus matematikus még ma is vihogni kezd, ha meghallja, hogy kognitív tudományi képzés folyik a BME Természettudományi Karán. Nekem szerencsém volt olyan kollégákkal együtt dolgozni, akik tudják, hogy a gondolkodás tárgya lehet más is, mint operátor, funktor, sajátérték és görbület, és akik hajlandók külön készülni ezekre a speciális órákra.

Összegezve

A legfontosabbnak azt tartom, hogy kedvük legyen a tárgyhoz. Ne féljenek tőle. (Gondoljuk meg, hogy a történelem folyamán minden új számfajta olyan nevet kapott, ami kifejezte az emberiség félelmét: negatív, képzetes, komplex, szürreális számok, sajnos, az irracionális nem illik a sorba, pedig a teljesség kedvéért szép lenne.) Ismerjék meg a matematika szerkezetét, az általa nyújtott lehetőségekről legyen valami fogalmuk. A deriválási szabályokat pedig (ha szükségesek) másutt gyakorolják be, vagy pedig használjanak erre alkalmas programot. A hatékonyság növelésére egyetlen lehetőséget látok: 10—12 fősnél nagyobb csoportot nem szabad képezni, vagyis a jelenlegi létszám mellett két csoport kell.

„Légvárak építésénél ne sajnáljuk a kacsalábat”

Ezt Halász Gábortól, Izraelben dolgozó kedves fizikus barátomtól tanultam. Az ideális helyzet tehát az lenne, ha kis csoportokban tanítanánk mindhárom tárgyat. Itt is (mint szerintem mindenhol) az előadásokat matematikusnak kell tartania, a gyakorlatokat pedig matematikához értő, de az alkalmazások iránt fogékony kollégának, tehát nem feltétlenül matematikusnak. Egységes, erős gépi támogatás kell. De miért épp a Wolfram nyelv? Mert egyetlen kereten belül lehet beszélni kép- és nyelvfeldolgozásról, folyamatokról, neuronhálózatokról és statisztikáról (olyan mélységben, ameddig kevés alkalmazó jut el). Lehet készíteni animációt, ábrát a cikkekbe, dolgozatokba, vagy akár teljes dolgozatot, akár prezentációt is lehet benne készíteni.

Lássunk még két példát a szövegfeldolgozás területéről.

Ha kíváncsiak vagyunk arra, hogy melyek azok a szavak az angol és a francia nyelvben, amelyek oda- és visszafelé olvasva azonosak, akkor ezeket így kaphatjuk meg:

Intersection @@(DictionaryLookup[{#, x__/; x === StringReverse[x]}]&

/@{“English”,”French”})

Ma már elképzelhetetlen, milyen mélységű aktuális számítástechnikai ismeret és milyen mennyiségű munka kellett a magyar nyelv a tergo (szóvégmutató) szótárának (Papp F., 1994) elkészítéséhez. Kedvenc programunk az angol nyelv beépített, mintegy 100 ezer szavas szótárából ezzel az utasítással készíti el másodpercek alatt az angolét:

StringReverse/@Sort[StringReverse/@DictionaryLookup[]]


Folytatás

Az ismertetett tárgyak a legelső félévben veendők fel. A második félévben tartunk — bár jobb meggyőződésem ellenére, de az én kezdeményezésemre — MATLAB órát, amire sokan jönnek a kognitív szak hallgatói közül.

Viszont az egyik évben azzal leptek meg bennünket a hallgatók, hogy szívesen hallgatnának előadásokat a kimaradt (és — teszem hozzá — máshol is általában kimaradó) témakörökről. Ezért aztán Molnár Zoltánnal közösen meghirdettünk egy fakultatív tárgyat Érdekességek a matematika alkalmazásaiból címmel. Erre mindenféle hallgató jön, még a kognitív tudományi mesterek is. Tematikája nagyjából: dinamikai rendszerek, logika és nyelvészet és hálózatok.

Másutt?

Érdeklődéssel olvasnám, hogy hogyan kell informatikusokat, biomérnököket okítani (elfeledve az egységes matematikaoktatás rémálmát). Ami például a biológusokat illeti, kiváló példája a személyekre (szakra) szabott tankönyvnek Izsák és társai műve (1982), amely minden fogalmat biológiai eredetű példák sokaságán mutat be. Annak is lehet némi magyarázata, hogy Alexits és Fenyő írása (1955) miért tudott német és francia nyelven is megjelenni. És lám, máris olvashatjuk Vizvári Béla írását a sok számítást igénylő tárgyak oktatásáról mérnök hallgatók számára az Érintő jelen számában.

Irodalomjegyzék

Abbott, E.: Flatland. A romance of many dimensions.

Alexits Gy., Fenyő I.: Matematika vegyészeknek, Tankönyvkiadó, Budapest, 1955.

Andler, D. Mathematics in cognitive science, In: Weber, M., Dieks, D., Gonzalez, W. J., Hartman, S. Stadler, F. and Stöltzner, M. (eds.), Probabilities, Laws and Structures, Springer Netherlands, Dordrecht, 2012, pp. 363–377.

Arbib, M., Érdi, P., Szenthágotai, J.: Neural organization: Structure, function, dynamics, A Bradford Book, MIT Press, Cambridge, MA, London, England, 1997. (Chapters 4 and 11)

Bush, V.: As we may think, Atlantic Magazine, (1945), 47–61.

Cseresnyési László: Nyelv és neurózis. Közös tudás, Magyar Narancs 2016/40 (október 6.)

Dehaene, S.: The Number Sense: How the Mind Creates Mathematics, Oxford University Press, New York, 1997.

Wolfram Demonstrations Project

Emmer, M.: Mathematics and Culture II. Visual Perfection: Mathematics and Creativity, Springer, 2005.

Hersh, R.: A matematika természete, Typotex Kiadó, Budapest, 2000.

Izsák J., Juhász-Nagy, P., Varga Z.: Bevezetés a biomatematikába, Tankönyvkiadó, Budapest, 1982.

Lóczi Lajos, Sándor Nóra: Informatics to Students of Cognitive Science, 2014.

Minsky, M.: Why people think computers can't, AI Magazine 3 (4) (1985), 2--15.

Neumann, J.: Probabilistic logic and the synthesis of reliable organisms from unreliable components, In Automata Studies, C. E. Shannon, J. McCarthy eds., 1956, pp. 43–98.

Papp Ferenc (szerk.): A ​magyar nyelv szóvégmutató szótára, Akadémiai Kiadó, Budapest, 1994.

Piaget, J., Herinques, G., Papert, S., & Ackerman-Valladao, E.: Morphismes et catégories: comparer et transformer. Delachaux et Niestlé Neuchâtel, 1990.

Rényi, Alfréd.Ars mathematica. Magvető Könyvkiadó, 1973.

TED. Ideas worth spreading

Tóth J.: Mennyi kell a Dedekind-tortából a programozónak?, Tétékás Nyúz XXIII/11 (2001. november 28.)

Turing, A. M.: Computing machinery and intelligence, Mind 59 (1950), 433–460.

Vizvári B.: Tétékás Nyúz XXIII/7 (2001)

Wigner, E.: The unreasonable effectiveness of mathematics in the natural sciences, Communications on Pure and Applied Mathematics 13 (1) (1960) 1–14.

 Tóth János