(Például magyar) sportújságírók kedves szórakozása olimpiák idején azzal szítani nemzeti büszkeségünket, hogy kiszámolják, egy lakosra hány aranyérem jut Magyarországon, és mennyi mondjuk a nálunk némileg gazdagabb Egyesült Államokban. A következtetés persze mindig az, hogy mivel az első hányados nagyobb, mint a második, ezért mi sokkal jobbak vagyunk sportban, mint ők.
Mi rejlik ezen érvelés mögött?
Az a hiedelem, ami közönséges halandók, de még kevésbé közönséges fizikusok között is meglehetősen általános: minden mindennek (homogén) lineáris függvénye, esetünkben tehát kétszer akkora országnak kétszer annyi aranyérem dukál. Rögtön fölvetődik a kérdés, hogy vajon 1952-ben, a Helsinkiben tartott olimpia idején begyűjtött 16 aranyérem [1] arra utal-é, hogy országunk lélekszáma fele akkorára csökkent azóta?
Komolyabb elemzés céljából begyűjthető a hálóról az aranyérmek száma, és ha a vizsgálatokat a Mathematica programmal végezzük, akkor onnan kibányászható az egyes országok lakosainak száma, és máris elkészíthető az alábbi ábra.
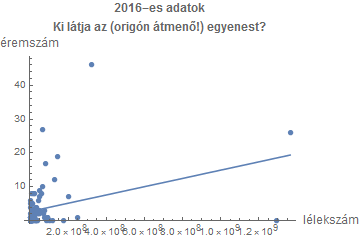(A programon belül az is látszik, melyik pont melyik országnak felel meg.) Ha valaki azt gondolná, hogy Rio de Janeiro levegője nem kedvez a lineáris összefüggésnek, akkor elkészítheti az analóg ábrát a 2012-es adatokkal: épp ilyen felhőt fog kapni, amely ismét inkább azt mutatja, hogy a lakosság létszáma és az olimpiai aranyérmek száma független egymástól.
[1] Feleki László: Tizenhat nap, Szépirodalmi Könyvkiadó (Budapest) , 1953.
TJ