1. Bevezető
Mielőtt rátérünk a cikk tartalmi részére – nevezetesen a mértékelmélet egyik alaptételének egy olyan bizonyítására, amely a lineáris altérre vett zárlat tulajdonságaival operál – röviden felidézünk néhány alapfogalmat.
Egy ![]() halmaz részhalmazaiból álló
halmaz részhalmazaiból álló ![]() halmazrendszer
halmazrendszer ![]() -algebra, ha zárt a komplementer és a megszámlálható unió képzésére. Egy
-algebra, ha zárt a komplementer és a megszámlálható unió képzésére. Egy ![]() halmaz karakterisztikus függvényét
halmaz karakterisztikus függvényét ![]() -val jelöljük, azaz
-val jelöljük, azaz
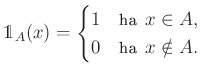
Egy ![]() halmazfüggvényt nemnegatív véges mértéknek nevezünk, ha az alábbi két feltételt teljesíti:
halmazfüggvényt nemnegatív véges mértéknek nevezünk, ha az alábbi két feltételt teljesíti:
(i) ![]() ,
,
(ii) ha ![]() egy olyan
egy olyan ![]() -ban haladó halmazsorozat, hogy tetszőleges
-ban haladó halmazsorozat, hogy tetszőleges ![]() esetén
esetén ![]() , akkor
, akkor
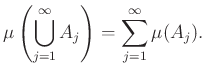
Az ![]()
![]() -algebrához természetes módon asszociálódik a valós
-algebrához természetes módon asszociálódik a valós ![]() -lépcsős függvények
-lépcsős függvények ![]() -vel jelölt vektortere. Emlékeztetünk, hogy egy
-vel jelölt vektortere. Emlékeztetünk, hogy egy ![]() függvényt
függvényt ![]() -lépcsős függvénynek nevezünk, ha
-lépcsős függvénynek nevezünk, ha ![]() -beli halmazok karaktersztikus függvényeinek véges lineáris kombinációja. Azaz ha van olyan
-beli halmazok karaktersztikus függvényeinek véges lineáris kombinációja. Azaz ha van olyan ![]() véges
véges ![]() -beli halmazrendszer és
-beli halmazrendszer és ![]() valós szám
valós szám ![]() -es, amelyre
-es, amelyre
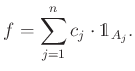
Hasonlóan természetes módon adódik egy egyszerű integrálfogalom az ![]() -lépcsős függvények vektorterén. A fenti felírású
-lépcsős függvények vektorterén. A fenti felírású ![]() függvény
függvény ![]() szerinti integrálján az
szerinti integrálján az
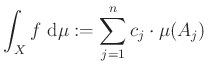
számot értjük. Az így kapott integrál jóldefiniált, azaz az integrál értéke nem függ ![]() előállításától. Megjegyezzük, hogy két
előállításától. Megjegyezzük, hogy két ![]() -lépcsős függvény szorzata is
-lépcsős függvény szorzata is ![]() -lépcsős függvény, így ha
-lépcsős függvény, így ha ![]() , akkor
, akkor ![]() továbbra is egy véges összeget jelöl, tehát a fentinél bonyolultabb integrálfogalomra nem lesz szükségünk. Végül bevezetünk egy jelölést: az
továbbra is egy véges összeget jelöl, tehát a fentinél bonyolultabb integrálfogalomra nem lesz szükségünk. Végül bevezetünk egy jelölést: az ![]()
![]() -lépcsős függvény tartóját, azaz az
-lépcsős függvény tartóját, azaz az ![]() halmazt röviden
halmazt röviden ![]() -val jelöljük.
-val jelöljük.
2. Abszolút folytonosság és altérre vonatkozó zárlat
Mostantól ![]() és
és ![]() mindig két nemnegatív véges mértéket jelöl. Azt mondjuk, hogy
mindig két nemnegatív véges mértéket jelöl. Azt mondjuk, hogy ![]() abszolút folytonos a
abszolút folytonos a ![]() -re nézve (jelekkel:
-re nézve (jelekkel: ![]() , ha
, ha
Megjegyezzük, hogy ez a folytonosság fogalom azért képes ilyen egyszerű, ránézésre meglehetősen algebrai alakot ölteni, mert a ![]() -additivitás rásegít a
-additivitás rásegít a
definícióra. Az abszolút folytonosság fogalmának jelentőségére a Radon-Nikodym tétel világít rá: a ![]() mértéknek pontosan akkor létezik sűrűségfüggvénye a
mértéknek pontosan akkor létezik sűrűségfüggvénye a ![]() -re vonatkozóan, ha
-re vonatkozóan, ha ![]() .
.
De mi köze van a mértékek abszolút folytonosságának a mátrixok alterekre vonatkozó zárlatához? Pozitív szemidefinit (és így önadjungált) mátrixok esetén a képtér és a magtér, azaz a
alterek egymásra merőlegesek, és így a ![]() tartalmazás ekvivalens azzal, hogy
tartalmazás ekvivalens azzal, hogy ![]() . Ez utóbbit másképp felírva azt kapjuk, hogy
. Ez utóbbit másképp felírva azt kapjuk, hogy
ami pedig az abszolút folytonosság fogalmára legalábbis formailag nagyon hasonlít. Két tetszőlegesen választott ![]() és
és ![]() pozitív szemidefinit mátrixra a
pozitív szemidefinit mátrixra a ![]() tartalmazás természetesen nem teljesül. De az altérre vonatkozó zárlat fogalma (az
tartalmazás természetesen nem teljesül. De az altérre vonatkozó zárlat fogalma (az ![]() választással) épp azt garantálja, hogy az
választással) épp azt garantálja, hogy az
halmaznak van legnagyobb eleme, nevezetesen ![]() . Más szóval,
. Más szóval, ![]() -nak van egy olyan extremális tulajdonságokkal bíró része, amelynek képtere része
-nak van egy olyan extremális tulajdonságokkal bíró része, amelynek képtere része ![]() képterének. Könnyű megmutatni, hogy a maradék, azaz az
képterének. Könnyű megmutatni, hogy a maradék, azaz az ![]() mátrix képtere a
mátrix képtere a ![]() mátrix képterétől már amennyire csak lehet, diszjunkt:
mátrix képterétől már amennyire csak lehet, diszjunkt:
Ez a képterekre vonatkozó állítás (a Douglas majorizációs és faktorizációs tétel értelmében) ekvivalens azzal, hogy ha egy ![]() mátrixra
mátrixra ![]() és
és ![]() egyidejűleg teljesül, akkor
egyidejűleg teljesül, akkor ![]() a nulla mátrix.
a nulla mátrix.
Ezt a sémát akarjuk tehát követni nemnegatív véges mértékek esetén is. Igaz-e, hogy ha ![]() maga nem is abszolút folytonos
maga nem is abszolút folytonos ![]() -re nézve, akkor is le lehet választani belőle egy lehető legnagyobb
-re nézve, akkor is le lehet választani belőle egy lehető legnagyobb ![]() -abszolút folytonos részt? Milyen értelemben lesz a maradék a
-abszolút folytonos részt? Milyen értelemben lesz a maradék a ![]() -től diszjunkt?
-től diszjunkt?
Először is, ahhoz hogy beszélhessünk legnagyobb elemről, be kell vezetnünk egy részbenrendezést a nemnegatív mértékek halmazán:
Azt mondjuk, hogy ![]() és
és ![]() szingulárisak (jelekkel:
szingulárisak (jelekkel: ![]() ), ha van olyan
), ha van olyan ![]() halmaz, amelyre
halmaz, amelyre ![]() . Ez a tulajdonság ekvivalens azzal, hogy ha
. Ez a tulajdonság ekvivalens azzal, hogy ha ![]() egy olyan nemnegatív véges mérték, amelyre
egy olyan nemnegatív véges mérték, amelyre ![]() és
és ![]() egyszerre teljesül, akkor
egyszerre teljesül, akkor ![]() szükségképpen a nulla mérték. Világos tehát az analógia, az a kérdés, hogy hogyan profitáljunk belőle. Természetes ötlet, hogy valahogy fogalmazzuk át a mértékek nyelvére a
szükségképpen a nulla mérték. Világos tehát az analógia, az a kérdés, hogy hogyan profitáljunk belőle. Természetes ötlet, hogy valahogy fogalmazzuk át a mértékek nyelvére a
formulát. Az első kérdés, hogy mivel helyettesítsük a skalárszorzatot? Ha az ![]() mátrixot
mátrixot ![]() -re, az
-re, az ![]() vektort
vektort ![]() -re akarjuk fordítani, akkor az
-re akarjuk fordítani, akkor az ![]() kifejezés átírására az
kifejezés átírására az ![]() a kézenfekvő választás. Ha a
a kézenfekvő választás. Ha a ![]() mátrixot a
mátrixot a ![]() -re akarjuk lefordítani, akkor a
-re akarjuk lefordítani, akkor a ![]() lineárisaltér megfelelője
lineárisaltér megfelelője ![]() -ben
-ben
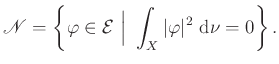
Ezek után már könnyű kiokoskodni, hogy az ![]() mátrix megfelelője a
mátrix megfelelője a

halmazfüggvény. Mint azt a következő fejezetben látni fogjuk, azzal hogy a fordítás kész, lényegében minden munkát elvégeztünk. Mielőtt rátérnénk a bizonyításra, teszünk még egy megjegyzést. Ahogy arra az abszolút folytonosság definíciójánál utaltunk, az egyszerűség hátterében ott munkálkodik a ![]() -additivitás. Az olvasóban felébredhet a gyanú, hogy valami a mátrixokra vonatkozó fogalom hátterében is munkálkodik, hiszen ott tényleg csak egy lineáris algebrai definícióról van szó, topológiának semmi nyoma. Való igaz, az hogy ez a fogalom ilyen egyszerű alakot öltött, az annak köszönhető, hogy
-additivitás. Az olvasóban felébredhet a gyanú, hogy valami a mátrixokra vonatkozó fogalom hátterében is munkálkodik, hiszen ott tényleg csak egy lineáris algebrai definícióról van szó, topológiának semmi nyoma. Való igaz, az hogy ez a fogalom ilyen egyszerű alakot öltött, az annak köszönhető, hogy ![]() véges dimenziós volt, és így a
véges dimenziós volt, és így a ![]() képtér automatikusan zárt. Ha
képtér automatikusan zárt. Ha ![]() nem véges dimenziós, akkor a
nem véges dimenziós, akkor a ![]() -ről külön fel kell tenni, hogy zárt képterű.
-ről külön fel kell tenni, hogy zárt képterű.
3. A Lebesgue-felbontás
Tétel: Legyen ![]() és
és ![]() két tetszőleges nemnegatív véges mérték az
két tetszőleges nemnegatív véges mérték az ![]()
![]() -algebrán. Ekkor
-algebrán. Ekkor ![]() -nek létezik egy és csak egy olyan
-nek létezik egy és csak egy olyan ![]() felbontása, ahol
felbontása, ahol ![]() és
és ![]() .
.
Bizonyítás: Mivel egy nemnegatív függvény integrálja nemnegatív, ![]() , és
, és ![]() esetén
esetén ![]() , ezért a
, ezért a ![]() definícióra ránézve világos, hogy
definícióra ránézve világos, hogy ![]() nemnegatív,
nemnegatív, ![]() , és hogy
, és hogy ![]() . Azt is könnyű ellenőrizni, hogy
. Azt is könnyű ellenőrizni, hogy ![]() végesen additív, mert ha
végesen additív, mert ha ![]() és
és ![]() diszjunkt
diszjunkt ![]() -beli halmazok, akkor
-beli halmazok, akkor
![$\displaystyle \Big\{\psi\in\mathscr{N}~\Big\vert~[\psi\neq0]\subseteq A_1\cup A...
...psi_1+\psi_2\in\mathscr{N}~\Big\vert~[\psi_i\neq0]\subseteq A_i,~i=1,2\Big\}.
$](/images/stories/latex/abe3ff95000a65ac3db9eb9c64462fe4_ujszaszititkosiii/img77.png)
Ebből viszont már következik ![]()
![]() -additivitása, ugyanis
-additivitása, ugyanis

teljesül minden olyan halmazsorozatra, amelynek tagjai páronként diszjuntak. Már csak azt kell megmutatnunk, hogy a ![]() és
és ![]() mértékek szingulárisak, és hogy a felbontás egyértelmű. Mindkét állítás könnyen következik majd abból, hogy
mértékek szingulárisak, és hogy a felbontás egyértelmű. Mindkét állítás könnyen következik majd abból, hogy ![]() a legnagyobb elem azon
a legnagyobb elem azon ![]() nemnegatív véges mértékek között, amelyekre
nemnegatív véges mértékek között, amelyekre ![]() és
és ![]() egyszerre teljesül. Ahhoz hogy ezt belássuk, válasszunk egy
egyszerre teljesül. Ahhoz hogy ezt belássuk, válasszunk egy ![]() függvényt, és vegyük észre, hogy
függvényt, és vegyük észre, hogy
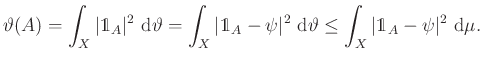
Az ![]() elemeire infimumot véve azt kapjuk, hogy
elemeire infimumot véve azt kapjuk, hogy ![]() .
.
Ezek után legyen ![]() egy olyan nemnegatív véges mérték, amelyre
egy olyan nemnegatív véges mérték, amelyre ![]() és
és ![]() . Ekkor
. Ekkor ![]() és
és ![]() , következésképp
, következésképp ![]() , ami épp azt jelenti, hogy
, ami épp azt jelenti, hogy ![]() .
.
Ha ![]() , a
, a ![]() -nek egy olyan felbontása, amelyre
-nek egy olyan felbontása, amelyre ![]() és
és ![]() teljesül, akkor
teljesül, akkor ![]() egy olyan nemnegatív véges mérték, amely egyszerre abszolút folytonos és szinguláris
egy olyan nemnegatív véges mérték, amely egyszerre abszolút folytonos és szinguláris ![]() -re nézve. Ebből pedig az következik, hogy
-re nézve. Ebből pedig az következik, hogy ![]() , és így
, és így ![]() . Ezzel a tételt bebizonyítottuk.
. Ezzel a tételt bebizonyítottuk.
A cikk az Emberi Erőforrások Minisztériumának ÚNKP-18-4-BGE-3 kódszámú „Új Nemzeti Kiválóság Program” pályázatának támogatásával készült.
A fénykép Henri Louis Lebesgue-et ábrázolja, forrás: https://dka.oszk.hu/021400/021493 (OSZK MEK)









