Információk

Főmenü

 Aktuális szám: 10. szám 2018. december 

A négyszámtétel egy csúnya bizonyítása

A négyszámtétel egy csúnya bizonyítása

Kalmár László Rédei Lászlóhoz írott levelében, amely a Kalmárium, Szabó Péter Gábor által összeállított gazdag [6] gyűjtemény 196–199. oldalain olvasható) találtam a következő állítást, amely négyszámtétel néven szerepel Kalmár sokkal korábbi [4] cikkében is.

1. Tétel   Ha $ a,b,c$ és $ d$ olyan pozitív egész számok, hogy

$\displaystyle ab=cd$
akkor van négy olyan természetes szám, $ x,y,z$ és $ u$, hogy
$\displaystyle a=xy, b=zu, c= xz, d=yu.$ (1)

Ott a bizonyítás nagyjából másfél oldal terjedelmű, teljes indukción alapul, és Kalmár egy kanadai kollégája (De Witte) a múlt század hatvanas éveinek végén a bizonyítás publikálását javasolja annak egyszerűsége miatt. A teljes Kalmár-bibliográfia [5] szerint úgy tűnik, mégsem készült a cikknek angol változata.

Adunk itt egy „csúnya” bizonyítást arra, hogy a feltétel nemcsak elégséges, hanem szükséges is.

Bizonyítás. Jelölje tetszőleges $ \xi$ természetes szám logaritmusát $ \overline{\xi}$. Akkor a bennünket érdeklő kérdés az, hogy mi a szükséges és elégséges feltétele annak, hogy a

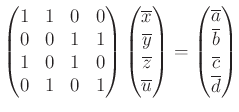
$\displaystyle \begin{pmatrix} 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 1 \\ 1 & 0 & 1 ... ...e{a} \\ \overline{b} \\ \overline{c} \\ \overline{d} \\ \end{pmatrix} $

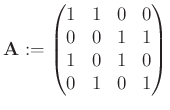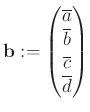lineáris egyenletrendszernek létezik megoldása. Erre a közismert válasz [3, 184. oldal, 1. tétel] vagy [2, 86. oldal, 3.4.3. tétel]: pontosan akkor, ha az $ {\bf A}:=\begin{pmatrix} 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 1 \\ 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \\ \end{pmatrix}$ együtthatómátrixnak és az $ ({\bf A \vert b})$ úgynevezett kibővített mátrixnak (ahol $ {\bf b}:=\begin{pmatrix} \overline{a} \\ \overline{b} \\ \overline{c} \\ \overline{d} \\ \end{pmatrix}$) a rangja megegyezik. Néhány sorművelet után könnyen látszik, hogy ez épp akkor teljesül, ha a feltétel fennáll.

Be kell még látnunk, hogy a feltétel teljesülése esetén léteznek alkalmas egész számok. Az egyenletrendszer explicit megoldása ilyen alakban írható:

$\displaystyle \overline{y}=\overline{a}-\overline{x}\quad \overline{z}=\overline{c}-\overline{x}\quad \overline{u}=\overline{b}-\overline{c}+\overline{x}. $

Legyen $ c=c_1c_2$, és írjuk fel az $ a$ és $ b$ számot $ a=c_1\alpha, b=c_2\beta$ alakban (a $ c_1,c_2,\alpha,\beta$ pozitív egész számokkal), akkor

$\displaystyle x=c_1\quad y=\alpha\quad z=c_2\quad u=\beta $

egy kívánt előállítás. $ \qedsymbol$

Természetesen a feltétel elegendőségének bizonyításához a második rész elegendő. A feltétel szükségessége pedig az (1) egyenlet megfelelő oldalainak összeszorzásával azonnal adódik.

A négyszámtétel messzemenően általánosítható ([4, 3. §, 12.]). Ezek közvetlen vagy közvetett hasznossága azonban nem nyilvánvaló, míg Kalmár eredeti tételét nemcsak saját maga használta, hanem (természetes számok helyett bizonyos polinomokra) Rédei is, amint ezt szintén a levélgyűjteményben olvashatjuk. Kalmár dolgozatában érdekes gráfelméleti szemléltetés is szerepel.

A csúfság például abban áll, hogy a számelmélet alaptétele nélkül az $ a$ és $ b$ szám fenti felbontása nem látszik bizonyíthatónak. Igazából a négyszámtétel egyenértékű az alaptétellel. Az [1] Erdős–Surányi könyv éppen a négyszámtételen keresztül jut el az alaptételhez, és a négyszámtételre (10. oldal, 2. tétel) éppen egy ilyen független – geometriai jellegű – bizonyítást ír le. Mint fentebb említettük, a korai Kalmár-féle bizonyítás [4] teljes indukción alapul.

A szépség, ha van, talán abban, hogy monomokat tartalmazó összefüggések lineárissá tehetők a logaritmus alkalmazásával – még ha nem is erre szokás a logaritmust és iteráltjait a számelméletben használni.

Be kell azt is vallanom, hogy a fenti módszer olyan bonyolultabb állítások bizonyítására, amilyen például Vass J. [7] 2.1. lemmája (amiben az oszthatóság fontos szerepet játszik), nem látszik egyszerűen alkalmazhatónak.

A szerző köszönettel tartozik Freud Róbertnek hasznos megjegyzéseiért.

Irodalomjegyzék

[1] Erdős P., Surányi J.: Válogatott fejezetek a számelméletből, POLYGON, Szeged, 1996.

 

[2] Freud R.: Lineáris algebra, ELTE Eötvös Kiadó, Budapest, 1996.

 

[3] Fried E.: Lineáris algebra, Tankönyvkiadó, Budapest, 1964. (ELTE TTK Egyetemi jegyzet)

 

[4] Kalmár L.: A számelmélet alaptételéről. Matematikai és Fizikai Lapok, 43 (1936), 27–45.

 

[5] Kalmár László: munkássága. Kalmár Bibliográfia. http://www.inf.u-szeged.hu/projectdirs/kalmar/pages/munkassaga_bibliografia.php

 

[6] Szabó P. G. (szerk.): KALMÁRIUM. Kalmár László levelezése magyar matematikusokkal, Polygon, Szeged, 2005.

 

[7] Vass, J.: A generalization of Euler's criterion to composite moduli, arXiv preprint arXiv:1507.00098 (2015).
Tóth János

 

matematikatörténet tétel-bizonyítás