Bevezető gondolatok
A magyarországi matematikaversenyeken a tanulók nagyon gyakran találkozhatnak kombinatorikus gondolkodást igénylő feladatokkal. Ezek a példák általában megmozgatják a fiatalok fantáziáját, hiszen a játék, a különféle esetek elemzése, az esélylatolgatás mindenki számára érdekes kihívást jelent. A tankönyvekben, példatárakban a kombinatorikai feladatok általában az alapján vannak csoportosítva, hogy milyen leszámolási képlettel lehet megkapni a felvetett kérdésre a választ. Ennek szellemében ismerkednek meg a diákok a permutációkkal, variációkkal, kombinációkkal, a skatulyaelvvel és általában a kombinatorikus gondolkodással.
Gyakran hallani olyan véleményt a tanulóktól, hogy a kombinatorikai feladatok azért nehezek, mert szinte mindegyik probléma más, nincsenek olyan általános módszerek, irányelvek, amelyek segítségével eredményesek lehetnek ezen a területen. Természetesen ez az álláspont nem felel meg a valóságnak, hiszen ha nagyon sok kombinatorikai versenyfeladat megoldását tekintjük át, akkor világossá válik számunkra, hogy a kombinatorikában is megvannak azok az eszközök, amelyek segítségével nagy eséllyel lehetünk sikeresek a feladatok megoldásában.
Ebben a cikkben a sikerhez vezető módszerek közül szeretnénk bemutatni néhányat.
1. Osztályozás módszere
Ha a feladat feltételeinek megfelelő kombinatorikai szerkezet sokféle helyzet szerint megvalósulhat, akkor célszerű ezeket külön megvizsgálni.
Az osztályok kialakításának szempontjai:
– Az eredeti probléma minden helyzetét bele kell foglalni valamelyik osztályba.
– A kialakított osztályok páronként idegenek legyenek.
– Az osztályozás egyetlen kritérium szerint történjen.
– A részproblémák megoldása könnyebb legyen, mint a teljes problémáé.
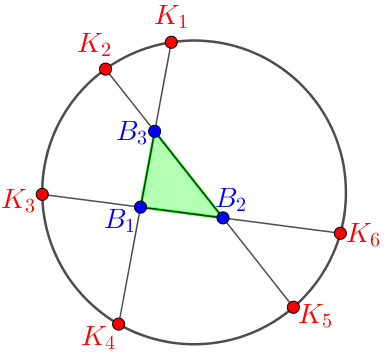
Példa. Egy körön kijelölünk ![]() (
(![]() ) darab pontot, és közülük bármely kettőt összekötjük egy egyenes szakasszal. Tudjuk, hogy a megadott szakaszok közül semelyik három nem halad át a kör ugyanazon belső pontján. Így bármely három szakasz, amelyik páronként metszi egymást, meghatároz egy háromszöget. Adjuk meg a szakaszok által meghatározott háromszögek számát!
) darab pontot, és közülük bármely kettőt összekötjük egy egyenes szakasszal. Tudjuk, hogy a megadott szakaszok közül semelyik három nem halad át a kör ugyanazon belső pontján. Így bármely három szakasz, amelyik páronként metszi egymást, meghatároz egy háromszöget. Adjuk meg a szakaszok által meghatározott háromszögek számát!
Megoldás. Nevezzük a körön felvett pontokat külső pontoknak, a körön belül képződő metszéspontokat belső pontoknak! A keletkező háromszögeket csoportosítsuk aszerint, hogy a csúcsok között milyen arányban fordulnak elő külső és belső pontok.
1. osztály: A háromszögek mindhárom csúcsa külső pont:
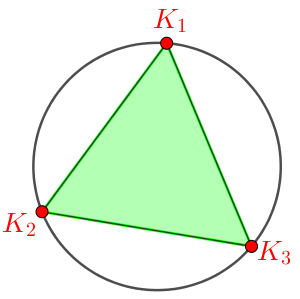
3 külső pont ![]() háromszög.
háromszög.
Az első csoportba tartozó háromszögek száma: ![]() .
.
2. osztály: A háromszögek két csúcsa külső, egy csúcsa belső pont:
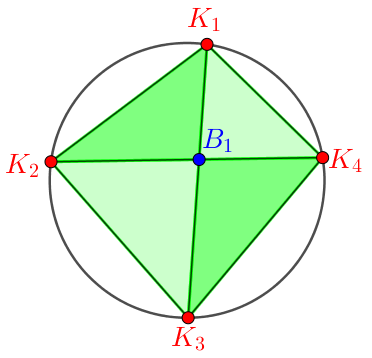
A keletkező háromszögek: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
4 külső pont ![]() 4 háromszög.
4 háromszög.
A második csoportba tartozó háromszögek száma: 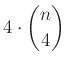 .
.
3. osztály: A háromszögek egy csúcsa külső, két csúcsa belső pont:
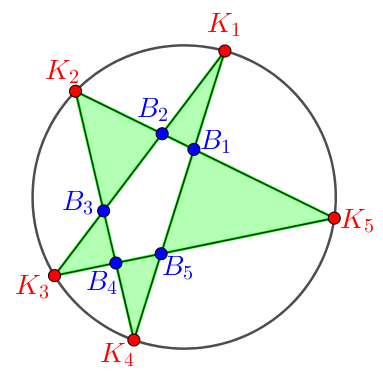
A keletkező háromszögek: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
5 külső pont ![]() háromszög.
háromszög.
A harmadik csoportba tartozó háromszögek száma: 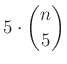 .
.
4. osztály: A háromszögek mindhárom csúcsa belső pont:
6 külső pont ![]() háromszög
háromszög
A negyedik csoportba tartozó háromszögek száma: ![]() .
.
Így a keletkező összes háromszögek száma:
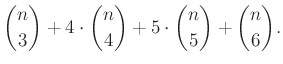
2. Frakcionált lépések módszere
– Az eredeti komplex, nehéz problémát részproblémákra bontjuk.
– Megoldjuk a részproblémákat.
– Amikor az utolsó részprobléma is megoldódik, megkapjuk az eredeti feladat megoldását is.
Példa. A 0, ![]() számok segítségével felírunk
számok segítségével felírunk ![]()
![]() -jegyű különböző számsorozatot. Ha a felírt sorozatok közül bármelyik hármat összehasonlítjuk, akkor azokra teljesül, hogy létezik olyan
-jegyű különböző számsorozatot. Ha a felírt sorozatok közül bármelyik hármat összehasonlítjuk, akkor azokra teljesül, hogy létezik olyan ![]() pozitív egész szám, amelyre a vizsgált sorozatok
pozitív egész szám, amelyre a vizsgált sorozatok ![]() -edik jegye
-edik jegye ![]() -es. Mutassuk meg, hogy ekkor létezik olyan
-es. Mutassuk meg, hogy ekkor létezik olyan ![]() pozitív egész szám is, amelyre az összes sorozat
pozitív egész szám is, amelyre az összes sorozat ![]() -adik jegye
-adik jegye ![]() -es!
-es!
Megoldás. Legyen ![]() vagy
vagy ![]() és
és ![]() a felírt számsorozatok halmaza! Definiáljuk az
a felírt számsorozatok halmaza! Definiáljuk az ![]() halmazon az alábbi két műveletet:
halmazon az alábbi két műveletet:
Bármely ![]() ,
, ![]() esetén
esetén
ahol ![$ \overline{x_i}=\begin{cases}0, & \text{ha }x_i=1\\ [5pt]
1, & \text{ha }x_i=0\end{cases}$](/images/stories/latex/1fdd02a391b496d89d403644bd49583d_fonyolajosfonyonenemethildikokobinatorikaiversenyfeladatokmegoldasimodszerei/img33.png) ,
, ![]() és
és
Ekkor ![]() esetén
esetén ![]() ,
, ![]() , és a feladat feltétele szerint tetszőleges
, és a feladat feltétele szerint tetszőleges ![]() esetén
esetén ![]() .
.
Vizsgáljuk meg ![]() tulajdonságait! (Megjegyzés: ezek a részproblémák)
tulajdonságait! (Megjegyzés: ezek a részproblémák)
(1) Bármely ![]() esetén az
esetén az ![]() ,
, ![]() relációk közül pontosan az egyik teljesül.
relációk közül pontosan az egyik teljesül.
Indirekt bizonyítást alkalmazva esetén
![]() , ami ellentmond a feladat egyik feltételének.
, ami ellentmond a feladat egyik feltételének.
Mivel ![]() elemeiből
elemeiből ![]() -féle
-féle ![]() pár képezhető és
pár képezhető és ![]() , így
, így ![]() és
és ![]() közül pontosan az egyik tartozik hozzá
közül pontosan az egyik tartozik hozzá ![]() -hoz.
-hoz.
(2) Bármely ![]() esetén
esetén ![]() .
.
Ismét indirekt bizonyítást alkalmazva, tegyük fel, hogy ![]() . Ekkor az (1)-es tulajdonság alapján
. Ekkor az (1)-es tulajdonság alapján ![]() és
és ![]() , ami ellentmondás. Tehát
, ami ellentmondás. Tehát ![]() .
.
(3) Ha ![]() , akkor
, akkor ![]() esetén
esetén ![]() jegyei között 1 db 1-es van, a többi jegy 0. Ennek igazolása az alábbi megfontolások alapján történhet:
jegyei között 1 db 1-es van, a többi jegy 0. Ennek igazolása az alábbi megfontolások alapján történhet:
– Az (1)-es és (2)-es tulajdonságok alapján ![]() és
és ![]() .
.
– Ha ![]() -nek legalább két jegye 1-es, akkor
-nek legalább két jegye 1-es, akkor ![]() minden elemének legalább két rögzített pozíciójú jegye is 1-es, ami alapján
minden elemének legalább két rögzített pozíciójú jegye is 1-es, ami alapján ![]() .
.
A kapott ellentmondás igazolja a (3)-as tulajdonság teljesülését.
A részproblémák megoldása után visszatérhetünk az eredeti feladat megoldásához.
Mivel ![]()
![]() -adik jegye 1-es, a többi 0, ezért létezik olyan egyértelmű
-adik jegye 1-es, a többi 0, ezért létezik olyan egyértelmű ![]() pozitív egész, amelyre minden
pozitív egész, amelyre minden ![]() -beli sorozat
-beli sorozat ![]() -adik jegye 1-es.
-adik jegye 1-es.
3. Párosítási módszer
A megoldás során bizonyos szabályok szerint párosítjuk a kombinatorikai elemeket, és így sok számítás egyszerűbbé válik.
Példa. Legyen ![]() az
az ![]() halmaznak egy
halmaznak egy ![]() elemű részhalmaza (
elemű részhalmaza ( ![]() ,
, ![]() ,
, ![]() ). Tegyük fel, hogy az
). Tegyük fel, hogy az ![]() elemei növekvő sorrendbe vannak rendezve, azaz
elemei növekvő sorrendbe vannak rendezve, azaz ![]() . Az
. Az ![]() kifejezést nevezzük az
kifejezést nevezzük az ![]() halmaz alternáló összegének. (Például az
halmaz alternáló összegének. (Például az ![]() halmaz alternáló összege
halmaz alternáló összege ![]() , az
, az ![]() halmazé 5, az üres halmazé legyen 0.) Milyen értéket kapunk, ha
halmazé 5, az üres halmazé legyen 0.) Milyen értéket kapunk, ha ![]() összes részhalmazának alternáló összegét összeadjuk?
összes részhalmazának alternáló összegét összeadjuk?
Megoldás. Soroljuk ![]() részhalmazait két osztályba aszerint, hogy tartalmazzák, vagy nem tartalmazzák az
részhalmazait két osztályba aszerint, hogy tartalmazzák, vagy nem tartalmazzák az ![]() számot! Párosítsuk egymáshoz a két osztályból az
számot! Párosítsuk egymáshoz a két osztályból az ![]() ,
, ![]() és
és ![]() halmazokat! Az alternáló összegeket összeadva:
halmazokat! Az alternáló összegeket összeadva:
Mivel az ![]() -ből kialakítható halmazpárok száma
-ből kialakítható halmazpárok száma ![]() , ezért a keresett összeg
, ezért a keresett összeg ![]() .
.
4. Leképezési módszer
A módszer elméleti háttere:
Legyen ![]() egy leképezés két véges halmaz között.
egy leképezés két véges halmaz között.
a) Ha ![]() injektív, azaz bármely
injektív, azaz bármely ![]() ,
, ![]() esetén
esetén ![]() , akkor
, akkor ![]() .
.
b) Ha ![]() szürjektív, azaz bármely
szürjektív, azaz bármely ![]() -hez létezik olyan
-hez létezik olyan ![]() , hogy
, hogy ![]() , akkor
, akkor ![]() .
.
c) Ha ![]() bijektív, azaz kölcsönösen egyértelmű, akkor
bijektív, azaz kölcsönösen egyértelmű, akkor ![]() .
.
Ezt a módszert akkor alkalmazzuk, ha az ![]() halmaz elemszáma nehezen állapítható meg, és ezért helyette a vele bijektív leképezésben álló
halmaz elemszáma nehezen állapítható meg, és ezért helyette a vele bijektív leképezésben álló ![]() halmaz elemszámát határozzuk meg.
halmaz elemszámát határozzuk meg.
Egyenlőtlenségek bizonyításakor gyakran hozunk létre szürjektív vagy injektív leképezést két kombinatorikai objektumrendszer között.
Példa. Egy ![]() oldalú szabályos háromszöget az ábra szerint felosztunk egység oldalú kis háromszögekre. Határozzuk meg az ábrán látható egység oldalú rombuszok számát!
oldalú szabályos háromszöget az ábra szerint felosztunk egység oldalú kis háromszögekre. Határozzuk meg az ábrán látható egység oldalú rombuszok számát!
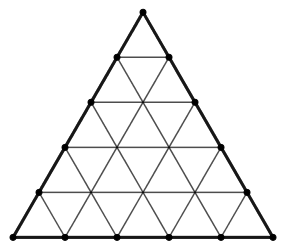
Megoldás. Először azokat a rombuszokat fogjuk összeszámolni, amelyek oldalai ![]() -vel nem párhuzamosak.
-vel nem párhuzamosak.
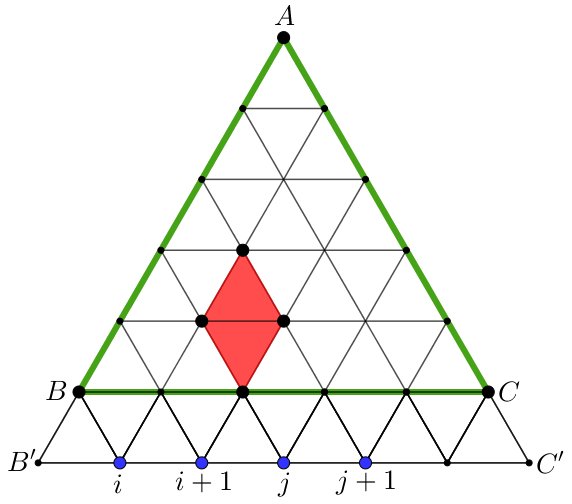
Egészítsük ki az eredeti ![]() szabályos háromszöget az ábrán látható módon egy
szabályos háromszöget az ábrán látható módon egy ![]() oldalú
oldalú ![]() szabályos háromszöggé! Ekkor a rombuszok oldalegyenesei a
szabályos háromszöggé! Ekkor a rombuszok oldalegyenesei a ![]() szakaszt 4 különböző pontban metszik. A metszéspontokat
szakaszt 4 különböző pontban metszik. A metszéspontokat ![]() -től számozva azonosítsuk a
-től számozva azonosítsuk a ![]() számokkal, és hozzunk létre egy
számokkal, és hozzunk létre egy ![]() rombuszok
rombuszok![]() ,
, ![]() bijektív leképezést!
bijektív leképezést!
Mivel az ![]() rendezett számnégyes tagjai nem függetlenek egymástól, ezért megadhatunk egy praktikusabb,
rendezett számnégyes tagjai nem függetlenek egymástól, ezért megadhatunk egy praktikusabb, ![]() ,
, ![]() bijektív leképezést is.
bijektív leképezést is.
![]() és
és ![]() alapján a
alapján a ![]() -vel nem párhuzamos oldalú rombuszok száma pontosan annyi mint a
-vel nem párhuzamos oldalú rombuszok száma pontosan annyi mint a ![]() halmaz kételemű részhalmazainak száma, azaz
halmaz kételemű részhalmazainak száma, azaz ![]() .
.
Így az összes egység oldalú rombuszok száma 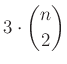 .
.
5. Kettős összeszámlálás módszere
Gyakran kínálkozik lehetőség arra, hogy egy kombinatorikus mennyiséget két egymástól különböző gondolatmenettel, kétféle úton is meg tudunk határozni. Ekkor a kapott összefüggések összehasonlításával értékes azonosságokat és fontos egyenlőtlenségeket kaphatunk.
Példa. Igazoljuk az alábbi azonosságot:
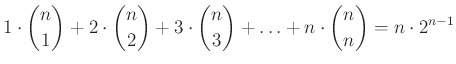 .
.Megoldás. A bizonyítást az alábbi kombinatorikai probléma kettős összeszámlálásával végezzük el:
Egy ![]() személyből álló csoport tagjaiból létrehozunk egy
személyből álló csoport tagjaiból létrehozunk egy ![]() tagú bizottságot, amelynek vezetője a bizottsági elnök. Hányféleképpen szerveződhet meg a bizottság?
tagú bizottságot, amelynek vezetője a bizottsági elnök. Hányféleképpen szerveződhet meg a bizottság?
Ekkor a bizottság kialakításának egyik módja:
– meghatározzuk, hogy hány fős legyen a bizottság (![]() ,
, ![]() ),
),
– kiválasztjuk a bizottsági tagokat ( ![]() lehetőség),
lehetőség),
– a bizottsági tagok maguk közül kiválasztják az elnököt (![]() lehetőség).
lehetőség).
Ezek alapján a lehetőségek száma összesen:
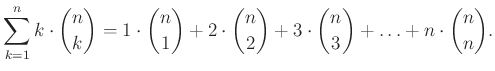
A bizottság kialakításának egy másik módja:
– a csapat tagjai közül kiválasztjuk az elnököt (![]() lehetőség),
lehetőség),
– a további ![]() személyről külön-külön döntünk, hogy bekerüljön-e a bizottságba (személyenként egymástól függetlenül 2-2 döntési lehetőség).
személyről külön-külön döntünk, hogy bekerüljön-e a bizottságba (személyenként egymástól függetlenül 2-2 döntési lehetőség).
Ebben az esetben a lehetőségek száma összesen: ![]() .
.
A kettős számolás és az összehasonlítás alapján:
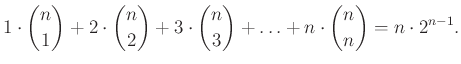
6. Rekurziós módszer
A megoldás lépései:
– Konkrét esetek vizsgálatával meghatározzuk a kezdőértékeket.
– Megállapítjuk a rekurziós összefüggést.
– Szükség esetén megadjuk az explicit képletet.
– Végül megadjuk a konkrét probléma megoldását.
Példa. Egy körlemezt felosztunk ![]() (
(![]() ,
, ![]() egybevágó körcikkre és az
egybevágó körcikkre és az ![]() szektorokat kiszínezzük
szektorokat kiszínezzük ![]() színnel úgy, hogy bármely két szomszédos rész színe különböző legyen. Hányféle különböző kiszínezési lehetőség van?
színnel úgy, hogy bármely két szomszédos rész színe különböző legyen. Hányféle különböző kiszínezési lehetőség van?
Megoldás. Legyen a megfelelő színezések száma ![]() !
!
a) Keressük meg először a kezdőértéket!
![]() esetén
esetén ![]() -et
-et ![]() -féle színnel színezhetjük ki, míg
-féle színnel színezhetjük ki, míg ![]() -t a felhasznált szín kivételével, a többivel.
-t a felhasznált szín kivételével, a többivel.
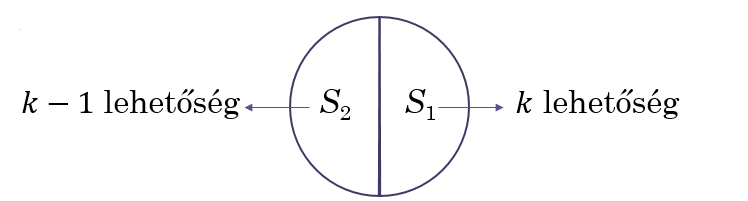
Így a szorzási szabály alapján ![]() .
.
b) Ezután határozzuk meg a rekurziós összefüggést!
Színezzük ki a tartományokat az ![]() sorrendben, és csak arra figyeljünk, hogy az éppen színezett tartomány az előzőtől eltérő színű legyen! Ekkor
sorrendben, és csak arra figyeljünk, hogy az éppen színezett tartomány az előzőtől eltérő színű legyen! Ekkor ![]() különböző lehetőség adódik a szektorok kiszínezésére.
különböző lehetőség adódik a szektorok kiszínezésére.
![]() és
és ![]() egymáshoz viszonyított színe alapján kétféle helyzet állhat elő.
egymáshoz viszonyított színe alapján kétféle helyzet állhat elő.
I. eset: ![]() és
és ![]() színe különböző
színe különböző
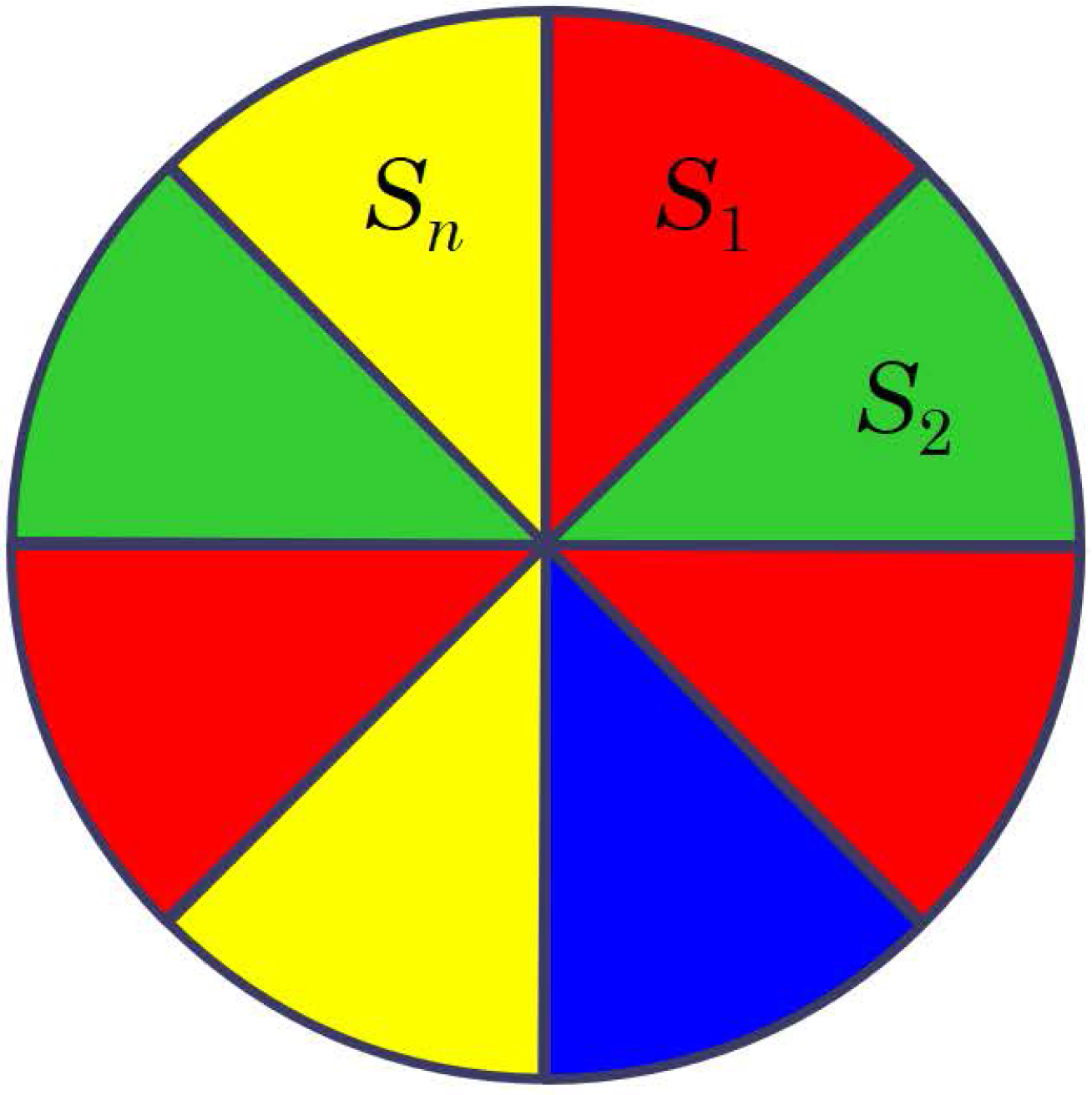
Az ilyen esetek száma: ![]() .
.
II. eset: ![]() és
és ![]() színe azonos
színe azonos
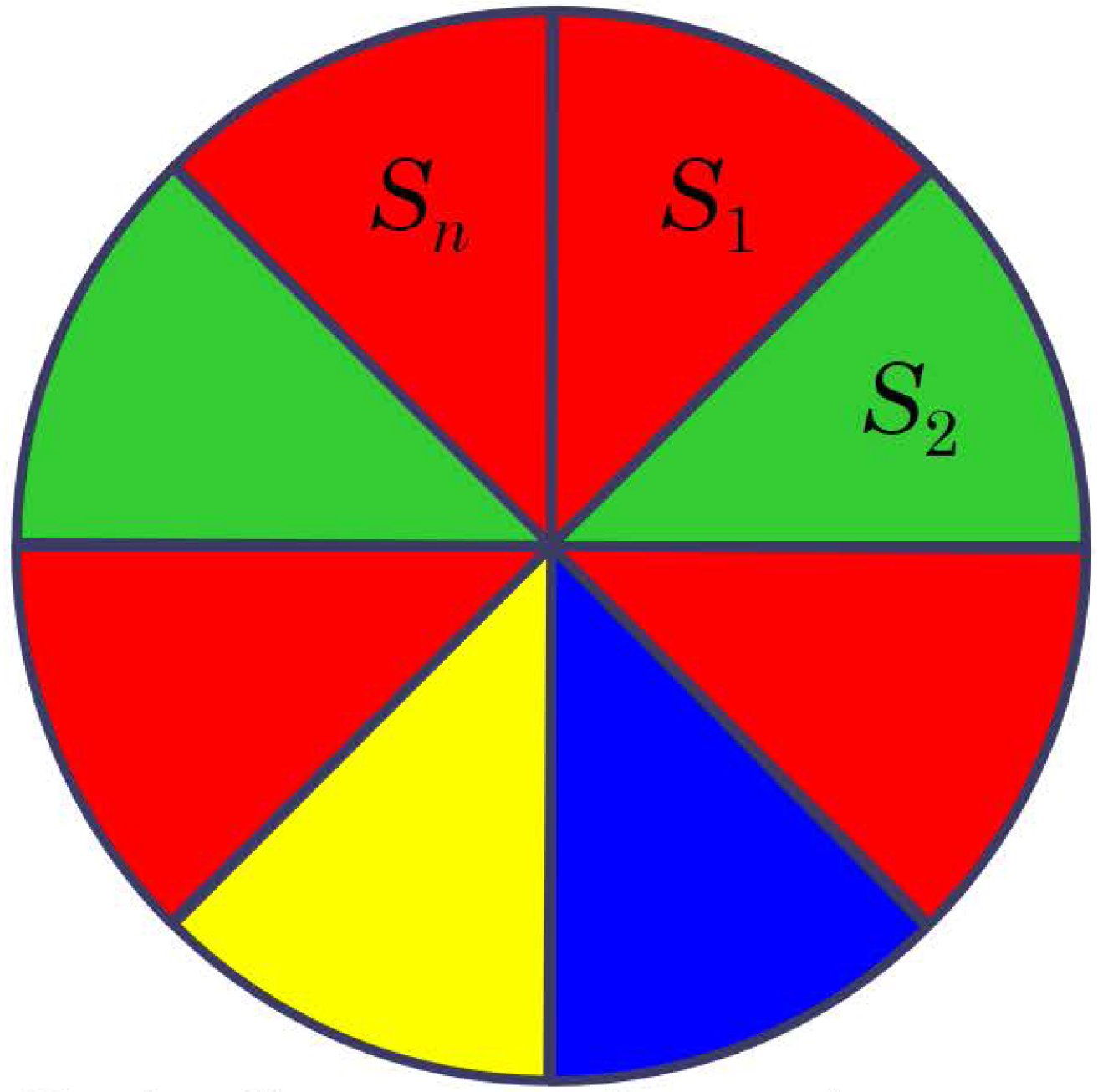
Ekkor ![]() és
és ![]() egy szektorrá egyesülnek, és olyan helyzet áll elő, mintha
egy szektorrá egyesülnek, és olyan helyzet áll elő, mintha ![]() tartomány lenne jól színezve. Így az ilyen esetek száma
tartomány lenne jól színezve. Így az ilyen esetek száma ![]() , és a rekurziós összefüggés:
, és a rekurziós összefüggés:
c) A továbbiakban az explicit képlet megadására törekszünk.
A rekurziós összefüggés alapján:
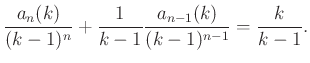
Vezessük be a 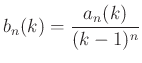 sorozatot! Ekkor
sorozatot! Ekkor
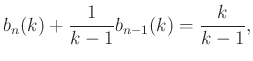 |
![$\displaystyle b_n(k)-1=-\frac{1}{k-1}[b_{n-1}(k)-1].$](/images/stories/latex/1fdd02a391b496d89d403644bd49583d_fonyolajosfonyonenemethildikokobinatorikaiversenyfeladatokmegoldasimodszerei/img128.png) |
Az index-léptetés módszerével alakítsuk tovább ![]() esetén:
esetén:
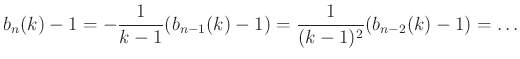 |
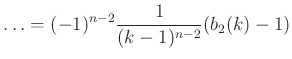 |
Felhasználjuk, hogy 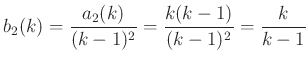 , és tudjuk, hogy
, és tudjuk, hogy ![]() :
:
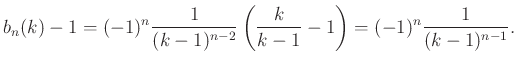
Innen meghatározhatjuk ![]() értékét:
értékét:
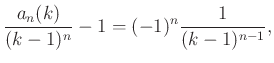 |
A levezetés ![]() esetében alkalmazható, de korábbi megállapításaink alapján az
esetében alkalmazható, de korábbi megállapításaink alapján az ![]() -ra kapott képlet
-ra kapott képlet ![]() esetben is helyes eredményt ad.
esetben is helyes eredményt ad.
7. Kiértékelés színekkel
A kombinatorikai elemekhez, kapcsolatokhoz pontokat, szakaszokat, tartományokat társítunk, és a megfelelő geometriai objektumokhoz színeket rendelünk.
Ezután megszámoljuk
– az azonos vagy különböző színű pontpárokat,
– az egyszínű vagy nem egyszínű háromszögeket,
– az azonos vagy különböző színű szárakkal rendelkező szögeket,
– az egyes tartományokhoz tartozó azonos színű mezőket.
Az adatokat ezután elemezzük, összehasonlítjuk, majd a megoldáshoz elvezető megállapításokat teszünk.
Példa. Egy parlament munkájában 30 személy vesz részt, és bármely két személy szövetségben áll vagy politikai ellenfele a másiknak. Tudjuk, hogy minden személynek pontosan 6 politikai ellenfele van. 3 személyt nevezzünk egységes triónak, ha közülük bármely két politikus szövetségben áll vagy ellenfele a másiknak. Határozzuk meg az egységes triók számát!
Megoldás. Az egyes személyekhez rendeljünk hozzá egy-egy térbeli pontot úgy, hogy semelyik 4 ne essen egy síkra! A szövetségeseket és a politikai ellenfeleket szemléltessük az alábbi módon:
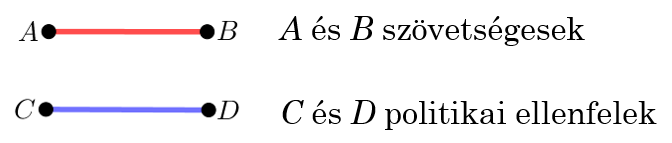
A keletkező gráfban az egyszínű háromszögeket számoljuk össze.
Ha egy háromszögben egy szög két szára különböző színű, akkor a szöget nevezzük tarka szögnek.
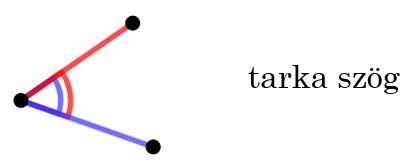
Vizsgáljuk a különböző típusú háromszögeket!
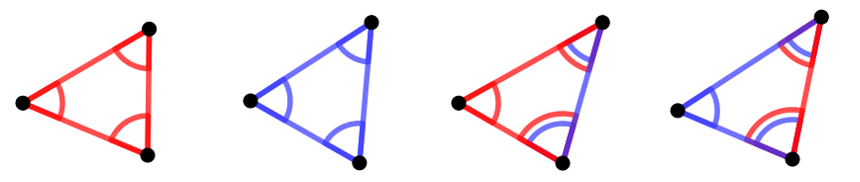
Ekkor az alábbi megállapításokat tehetjük:
– Egyszínű háromszögben nincs tarka szög.
– Nem egyszínű háromszögben 2 tarka szög van.
– Minden pontból 23 piros és 6 kék él indul ki.
– Egy csúcsban találkozó tarka szögek száma: ![]() .
.
– Az összes tarka szögek száma: ![]() .
.
– A nem egyszínű háromszögek száma: 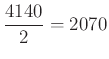 .
.
– Az összes háromszögek száma: 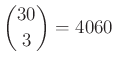 .
.
– Így az egyszínű háromszögek és az egységes triók száma: ![]() .
.
8. Kiértékelés számokkal
A megoldás során az egyes kombinatorikai elemekhez számokat rendelünk. A számokat elemezzük, összehasonlítjuk, és az invariáns tulajdonságaikat megállapítjuk.
Így a vizsgált probléma könnyen megoldhatóvá válik.
Példa. Egy szabályos hatszöget oldalaival párhuzamos egyenesek segítségével felosztunk 24 egybevágó szabályos háromszögre. A kis háromszögek csúcsaihoz 19 különböző valós számot rendelünk. Igazoljuk, hogy van legalább 7 olyan háromszög, amelynek csúcsaihoz rendelt számok az óramutató járása szerint haladva csökkenő sorozatot alkotnak!
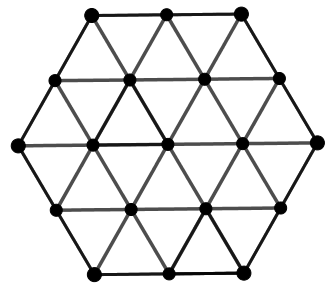
Megoldás. Osszuk be a háromszögeket két csoportba aszerint, hogy a csúcsaikhoz rendelt számok az óramutató járása szerint csökkenő vagy növekvő sorozatot alkotnak-e!
Tegyük fel, hogy az első csoportba ![]() háromszög tartozik, míg a második csoportba
háromszög tartozik, míg a második csoportba ![]() háromszög jut! Irányítsuk a háromszög éleit úgy, hogy a nyíl mindig a kisebb szám felé mutasson! Írjunk a nyilak bal oldalára
háromszög jut! Irányítsuk a háromszög éleit úgy, hogy a nyíl mindig a kisebb szám felé mutasson! Írjunk a nyilak bal oldalára ![]() -et, a jobb oldalára
-et, a jobb oldalára ![]() -et!
-et!
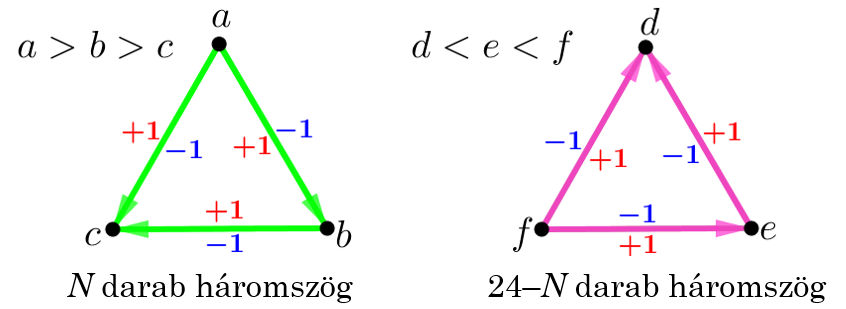
Ekkor az első csoportba tartozó háromszögekbe eső számok összege ![]() , a második csoportba tartozóké pedig
, a második csoportba tartozóké pedig ![]() . Emiatt a háromszögekbe írt számok összege:
. Emiatt a háromszögekbe írt számok összege:
Másrészt a hatszög belsejében levő élek két oldalára írt számok összege:
A hatszög oldalain elhelyezkedő 12 háromszögoldal kört alkot, így a melléjük írt számok közül legalább az egyik ![]() . Emiatt ezen 12 élre írt számok összege legalább
. Emiatt ezen 12 élre írt számok összege legalább
Így
Ezzel az állítást igazoltuk.
9. A lehetetlenre visszavezetés módszere
– A megoldás során feltesszük a direkt úton nehezen bizonyítható állítás tagadását.
– Ebből logikailag helyes következtetésekkel ellentmondásra jutunk.
– Ez pedig azt jelenti, hogy a bizonyítandó állítás igaz.
Példa. Az ![]() háromszög csúcsait ebben a sorrendben pirosra, kékre és zöldre színezzük. Ezután a háromszögben felveszünk néhány belső pontot, és ezeket összekötjük egymással, illetve az
háromszög csúcsait ebben a sorrendben pirosra, kékre és zöldre színezzük. Ezután a háromszögben felveszünk néhány belső pontot, és ezeket összekötjük egymással, illetve az ![]() háromszög csúcsaival, és így a háromszöget felosztjuk kisebb háromszögekre. Ezután a belső pontokat is kiszínezzük az említett három szín valamelyikével. Bizonyítsuk be, hogy tetszőleges színezés mellett keletkezik olyan kis háromszög, melynek mindhárom csúcsa különböző színű!
háromszög csúcsaival, és így a háromszöget felosztjuk kisebb háromszögekre. Ezután a belső pontokat is kiszínezzük az említett három szín valamelyikével. Bizonyítsuk be, hogy tetszőleges színezés mellett keletkezik olyan kis háromszög, melynek mindhárom csúcsa különböző színű!
Megoldás. Tegyük fel, hogy nem keletkezik olyan háromszög, amelynek mindhárom csúcsa különböző színű!
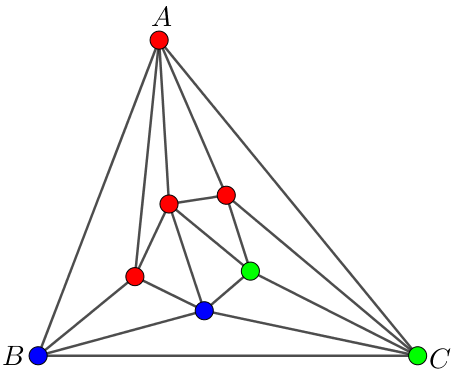
A továbbiakban használjuk a piros és kék pontot összekötő szakasz elnevezésére a piros-kék oldal megnevezést, és legyen a részháromszögek összes ilyen típusú oldalainak száma ![]() !
!
Határozzuk meg ![]() értékét kétféleképpen!
értékét kétféleképpen!
Mivel a belső piros-kék szakaszokra két-két háromszög illeszkedik, az ![]() oldalra pedig csak egy, ezért, ha a belső piros-kék szakaszok száma
oldalra pedig csak egy, ezért, ha a belső piros-kék szakaszok száma ![]() , akkor
, akkor ![]() , azaz
, azaz ![]() páratlan szám.
páratlan szám.
Másrészt, ha az ábrán nem keletkezik háromszínű háromszög, akkor piros-kék oldal csak piros-piros-kék, piros-kék-kék csúcsú háromszögekben található. Ezek mindegyike 2 piros-kék oldalt tartalmaz, ezért ha számuk p, akkor ![]() , azaz
, azaz ![]() páros szám.
páros szám.
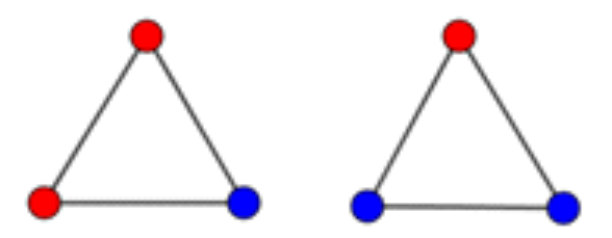
![]() nem lehet egyszerre páros, illetve páratlan szám, így ellentmondásra jutottunk. Ez azt jelenti, hogy a színezés során mindenképpen keletkezik piros-kék-zöld háromszög.
nem lehet egyszerre páros, illetve páratlan szám, így ellentmondásra jutottunk. Ez azt jelenti, hogy a színezés során mindenképpen keletkezik piros-kék-zöld háromszög.
10. Kiindulás a szélső helyzetből
– A megoldás során a vizsgált kombinatorikai elem maximális vagy minimális értékéből indulunk ki.
– Az ezen értékhez tartozó vizsgálat alapján az állítást elutasítjuk vagy elfogadjuk.
– Szükség esetén a kezdőértéket a céloknak megfelelően módosítjuk, és a problémát egy jó konstrukció megadásával megoldjuk.
Példa. Egy futballtornán minden csapat pontosan egy mérkőzést játszott a többi csapat mindegyikével. Minden mérkőzésen a győztes ![]() , a vesztes 0 pontot kapott, míg döntetlen eredmény esetén mindkét csapat
, a vesztes 0 pontot kapott, míg döntetlen eredmény esetén mindkét csapat ![]() –
–![]() pontot kapott. A tornát az
pontot kapott. A tornát az ![]() csapat nyerte meg úgy, hogy egyedüliként a legtöbb pontot szerezte, és a legkevesebb győzelmet érte el. Határozzuk meg a tornán résztvevő csapatok számának minimumát!
csapat nyerte meg úgy, hogy egyedüliként a legtöbb pontot szerezte, és a legkevesebb győzelmet érte el. Határozzuk meg a tornán résztvevő csapatok számának minimumát!
Megoldás. Legyen az ![]() csapat eredménylistája:
csapat eredménylistája:
![]() győzelem,
győzelem,
![]() döntetlen,
döntetlen,
![]() pont.
pont.
Ekkor a feltétel szerint a többi csapat mindegyike legalább ![]() győzelmet szerzett, és
győzelmet szerzett, és
| |
|
Tegyük fel, hogy az ![]() csapat egyik döntetlenjét a
csapat egyik döntetlenjét a ![]() csapat ellen szerezte. Ekkor a
csapat ellen szerezte. Ekkor a ![]() csapat legalább
csapat legalább ![]() pontot ért el, és
pontot ért el, és
| |
|
Vizsgáljuk ezután az ![]() csapat győzelmeinek számát! Tegyük fel, hogy
csapat győzelmeinek számát! Tegyük fel, hogy ![]() ! Legyen a résztvevő csapatok száma
! Legyen a résztvevő csapatok száma ![]() ! Ekkor az
! Ekkor az ![]() csapat pontszáma legfeljebb
csapat pontszáma legfeljebb ![]() , a többieké (
, a többieké (![]() )-nél kevesebb lehetett csak, és a csapatok együttesen
)-nél kevesebb lehetett csak, és a csapatok együttesen ![]() -nél kevesebb pontot gyűjthettek.
-nél kevesebb pontot gyűjthettek.
Viszont a mérkőzéseken összesen
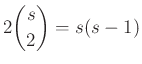
pont került kiosztásra. Így a kapott ellentmondás alapján ![]() .
.
![]() és
és ![]() esetén egy lehetséges eredménylista:
esetén egy lehetséges eredménylista:
| Pontszám | |||||||
| – | 1 | 1 | 1 | 1 | 2 | 6 | |
| 1 | – | 2 | 0 | 0 | 2 | 5 | |
| 1 | 0 | – | 0 | 2 | 2 | 5 | |
| 1 | 2 | 2 | – | 0 | 0 | 5 | |
| 1 | 2 | 0 | 2 | – | 0 | 5 | |
| 0 | 0 | 0 | 2 | 2 | – | 4 |
Tehát a tornán résztvevő csapatok minimális száma 6.
11. Helyi kiigazítások módszere
A megoldás során a kezdeti állapotból helyi kiigazításokkal lépésről lépésre közelítünk a cél felé.
A módszer felhasználható:
– kombinatorikus objektumok tulajdonságainak igazolására,
– kombinatorikai szélsőértékproblémák megoldására,
– adott tulajdonságú kombinatorikus szerkezetek kialakítására.
Példa. Írjuk fel a ![]() -at különböző pozitív egész számok összegeként úgy, hogy a számok szorzata maximális legyen! Mekkora ez a maximális érték?
-at különböző pozitív egész számok összegeként úgy, hogy a számok szorzata maximális legyen! Mekkora ez a maximális érték?
Megoldás. Vezessük be a kiválasztott számok halmazára, összegére és szorzatára az alábbi jelöléseket:
![]() ,
, ![]() (
( ![]() ,
, ![]() )
)
![]()
![]()
Mivel a 2008 véges sokféleképpen írható fel különböző egész számok összegeként, ezért a ![]() -nek létezik maximuma.
-nek létezik maximuma.
Vizsgáljuk az ![]() tulajdonságait.
tulajdonságait.
(1) Ha ![]() ,
, ![]() , de
, de ![]() , akkor alkalmazzuk az alábbi helyi kiigazítást:
, akkor alkalmazzuk az alábbi helyi kiigazítást:
Legyen . Ekkor
![]() és
és
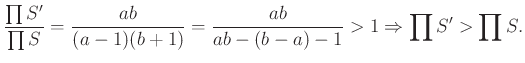
Tehát ![]() és
és ![]() között legfeljebb egy pozitív egész szám nem szerepel
között legfeljebb egy pozitív egész szám nem szerepel ![]() -ben.
-ben.
(2) Ha ![]() , akkor alkalmazzuk az alábbi helyi kiigazítást:
, akkor alkalmazzuk az alábbi helyi kiigazítást:
Legyen . Ekkor
![]() és
és
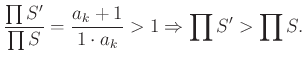
Tehát ![]() .
.
(3) a) Ha ![]() és
és ![]() , akkor alkalmazzuk az alábbi helyi kiigazítást:
, akkor alkalmazzuk az alábbi helyi kiigazítást:
Legyen . Ekkor
![]() és
és
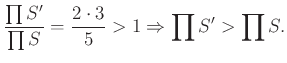
b) Ha ![]() ,
, ![]() (
( ![]() ),
), ![]() (
(![]() ), akkor alkalmazzuk az alábbi helyi kiigazítást:
), akkor alkalmazzuk az alábbi helyi kiigazítást:
Legyen ![]() . Ekkor
. Ekkor ![]() és
és
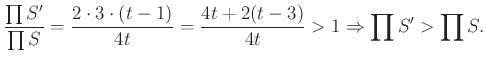
c) Ha ![]() , akkor alkalmazzuk az alábbi helyi kiigazítást:
, akkor alkalmazzuk az alábbi helyi kiigazítást:
Legyen . Ekkor
![]() és
és
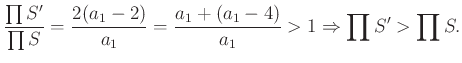
Tehát (3) a), b), c) alapján ![]() vagy
vagy ![]() .
.
Az (1), (2), (3) feltételek alapján, ha ![]() ,
, ![]() és
és ![]() (
(![]() ), akkor
), akkor
Az ![]() helyi kiigazítást alkalmazva:
helyi kiigazítást alkalmazva: ![]() és
és
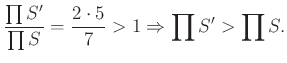
Tehát ![]() .
.
Az (1), (2), (3) feltételek alapján, ha ![]() ,
, ![]() és
és ![]() (
(![]() ), akkor
), akkor
Tehát ![]() maximális értéke
maximális értéke ![]() .
.
12. Konstrukciós módszer
A direkt konstrukciós módszer alkalmazása során:
– Elemezzük a célként kitűzött kombinatorikai szerkezetet.
– Részleges feltételeket teljesítő részeket hozunk létre.
– A szükséges korrekciók végrehajtásával olyan szerkezetet alakítunk ki, amely minden feltételnek megfelel.
Az induktív konstrukciós módszer alkalmazása során:
– ![]() -től függő kombinatorikai szerkezetet hozunk létre.
-től függő kombinatorikai szerkezetet hozunk létre.
– Először ![]() kezdőértékére megadjuk a megfelelő struktúrát.
kezdőértékére megadjuk a megfelelő struktúrát.
– Majd megadjuk, hogy ![]() értékének 1-gyel történő változtatása esetén milyen módosításokat kell végezni.
értékének 1-gyel történő változtatása esetén milyen módosításokat kell végezni.
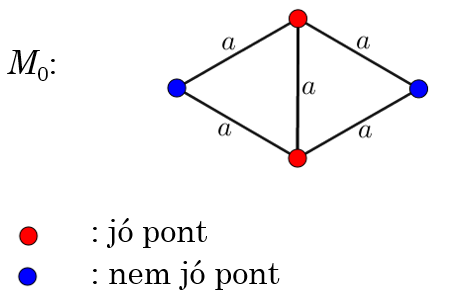
Példa. Van-e olyan véges ![]() ponthalmaz a síkon, amelynek bármely
ponthalmaz a síkon, amelynek bármely ![]() pontjára teljesül, hogy három
pontjára teljesül, hogy három ![]() -beli ponthoz van a legközelebb?
-beli ponthoz van a legközelebb?
Megoldás. Részfeltételeket teljesítő konstrukció:
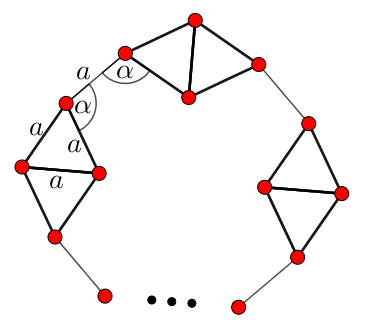
A konstrukció javítása történhet ![]() darab rombusz összeépítésével.
darab rombusz összeépítésével.
| (1) |
A külső konvex sokszög szögeit kétféleképpen felírva:
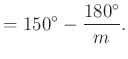 |
(2) |
Az (1), (2) feltételek alapján adódó megoldások:
| 4 | 5 | 6 | |
13. Valószínűségi módszer
A valószínűségszámítás eszközeivel:
– meghatározott tulajdonságú kombinatorikus modell létezését igazolhatjuk
a) ![]() jó modell
jó modell![]() .
.
b) rossz modell
.
– adott tulajdonságú kombinatorikai elemek számát megbecsülhetjük egy valószínűségi változó várható értékének meghatározásával. Ez utóbbira mutatunk példát.
Példa. Egy asztalitenisz bajnokságban ![]() játékos vesz részt. Eddig összesen
játékos vesz részt. Eddig összesen ![]() mérkőzés fejeződött be, és bármely két játékos legfeljebb egyszer játszott egymással. Adjunk becslést
mérkőzés fejeződött be, és bármely két játékos legfeljebb egyszer játszott egymással. Adjunk becslést ![]() legnagyobb értékére, ha tudjuk, hogy biztosan van a résztvevők között
legnagyobb értékére, ha tudjuk, hogy biztosan van a résztvevők között ![]() játékos, akik közül semelyik kettő nem játszott egymással!
játékos, akik közül semelyik kettő nem játszott egymással!
1. megoldás. A hagyományos leszámolási módszerrel az ![]() becslés adható.
becslés adható.
Indirekt bizonyítási módszert alkalmazva tegyük fel, hogy bármely 4-tagú csoportra jut mérkőzés.
– Ekkor a 4-tagú csoportok száma: 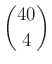 .
.
– Minden lejátszott mérkőzés 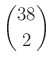 4-tagú csoportban szerepel.
4-tagú csoportban szerepel.
– Így a lejátszott mérkőzések száma legalább: 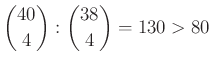 .
.
A kapott ellentmondás alapján garantált a mérkőzés nélküli 4 fős csoport létezése.
![]() esetén hasonló gondolatmenetet alkalmazva:
esetén hasonló gondolatmenetet alkalmazva:
– Az 5-tagú csoportok száma: 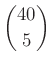 .
.
– Minden lejátszott mérkőzés 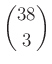 5-tagú csoportban szerepel.
5-tagú csoportban szerepel.
– Így a lejátszott mérkőzések száma legalább: 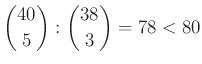 .
.
Tehát az alkalmazott módszer már nem garantálja a mérkőzés nélküli 5 fős csoport létezését.
2. megoldás. Valószínűségi módszerrel igazoljuk az ![]() becslés helyességét.
becslés helyességét.
Véletlenszerűen alakítsunk ki egy játékosokból álló csoportot úgy, hogy minden résztvevőt ![]() valószínűséggel választunk be az adott társaságba.
valószínűséggel választunk be az adott társaságba.
Ezután távolítsuk el a csoportból azokat a személyeket, akik vesztettek egy másik kiválasztott játékossal szemben. Így a megmaradó játékosok közül már semelyik kettő nem játszott egymás ellen.
Vizsgáljuk meg a megmaradó játékosok számának várható értékét! Ekkor
– Átlagosan ![]() játékos kerül kiválasztásra.
játékos kerül kiválasztásra.
– Minden lejátszott mérkőzés esetén ![]() a valószínűsége annak, hogy az kiválasztott játékosok között zajlott le.
a valószínűsége annak, hogy az kiválasztott játékosok között zajlott le.
– Tehát a kiválasztott játékosok között lejátszott mérkőzések átlagos száma ![]() .
.
– Az 5 vesztes legfeljebb 5 személy lehet, így őket a csoportból eltávolítva legalább 5 olyan ember marad, akik nem játszottak egymás között mérkőzést.
3. megoldás. Egy másik valószínűségi módszerrel igazoljuk az ![]() becslés helyességét.
becslés helyességét.
Rendeljünk a versenyzőkhöz 1-től 40-ig sorszámot és legyen az ![]() -edik játékos által lejátszott mérkőzések száma:
-edik játékos által lejátszott mérkőzések száma: ![]() ! Ekkor
! Ekkor
Ezután válasszuk ki azokat a játékosokat, akik legfeljebb csak alacsonyabb sorszámú társaikkal játszottak mérkőzést. Az ![]() -edik játékos pontosan akkor lett kiválasztva, ha ő kapta a legnagyobb sorszámot maga és a
-edik játékos pontosan akkor lett kiválasztva, ha ő kapta a legnagyobb sorszámot maga és a ![]() számú ellenfele közül. Tehát
számú ellenfele közül. Tehát
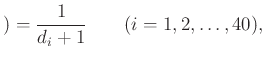
és így semelyik két kiválasztott játékos között nem volt mérkőzés.
Ekkor a kiválasztott játékosok számának várható értéke a számtani-harmonikus közép közti egyenlőtlenség alapján:
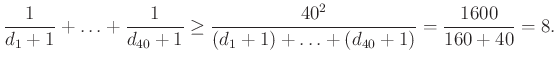
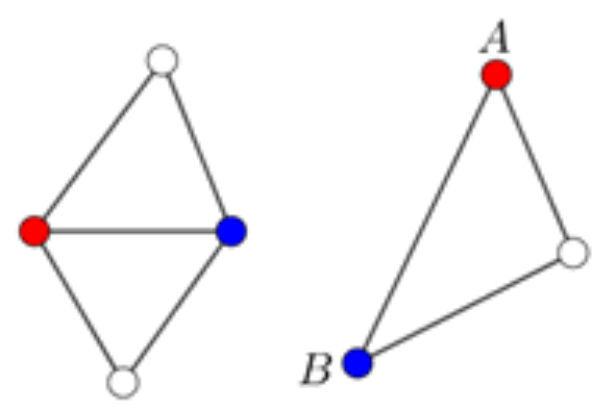
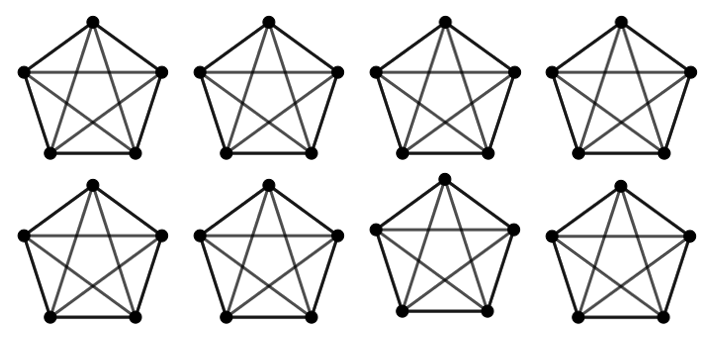
Megjegyzés. Az ![]() eredmény tovább már nem javítható. Az ábrán a pontok jelzik a játékosokat, a szakaszok pedig a közöttük lejátszott mérkőzéseket.
eredmény tovább már nem javítható. Az ábrán a pontok jelzik a játékosokat, a szakaszok pedig a közöttük lejátszott mérkőzéseket.
A gráf alapján jól látható, hogy minden csoportból legfeljebb 1 versenyző választható ki.
Ez az írás 2019-ben a gödöllői Rátz László Vándorgyűlésen elhangzott szemináriumi foglalkozás alapján készült. A bemutatott módszerek segítségével szinte bármilyen nehézségű leszámolási, létezési és szélsőértékfeladat, illetve kombinatorikus egyenlőtlenség megoldható. A cikkben közölt feladatokkal és megoldásaikkal jól használható anyagot próbáltunk biztosítani a középiskolában tanító tanároknak az iskolai szakköri munkához.









